
§8.2 线性回归分析的数学模型 在实际问题中我们常会遇到多个变 量同处于一个过程之中,它们互相联系, 互相制约。一些变量它们不能用用一个 确定的函数关系式表达出来。这些变量 其实就是是随机变量,之间的关系我们 常称为相关关系。为深入本质,我们也 需要去寻找这些变量间的数量关系式。 回归分析就是进行统计的一种方法。在 这种关系中简单的线性回归
§8.2 线性回归分析的数学模型 在实际问题中我们常会遇到多个变 量同处于一个过程之中,它们互相联系, 互相制约。一些变量它们不能用用一个 确定的函数关系式表达出来。这些变量 其实就是是随机变量,之间的关系我们 常称为相关关系。为深入本质,我们也 需要去寻找这些变量间的数量关系式。 回归分析就是进行统计的一种方法。在 这种关系中简单的线性回归

例8.4维伦纤维德耐热水性能好坏用指标“缩醛化度”来衡量。这个指标越高,耐水 性就越好。而甲醛浓度时影响缩醛化度的一个重要因素。在生产中常用甲醛浓度x(克升) 不去控制着一指标。下面是试验获得的一组数据: 甲醛浓度x(克升) 18 20 22 24 26 28 30 缩醛化度y(可分子%) 26.8628.3528.7528.87 29.75 30 30.36 若我们去重复试验,在同一甲醛浓度x下,所得缩醛化度y不完全一致。这明x与 y之间不能用个完全确定的函做关系来表达。直角坐标图(见图8.1)图略 从图我们可以把试验结果y看成有两部分叠加而成的,以部分有x的线性函数引起, 记月+乌x,另一部分是由随即因素引起的,记:,即: y=6+乐+e (8.23) 我们把ε看成随即误差,假定它服从N(0,σ2)分布。这就意味着假定: N(+x,σ2) 老

y的数学期望是x的线性函数。 为获得,8的估计,我们要进行若干次独立 试验。设所得结果为 (,x)=1,2,…n 这里61,E2,…,E都是独立随即变量,均服从 N(0,σ2)分布,这就是一元线性回归模型。 一般讲,影响结果y的因数不止一个,设共p个 元素。要确定它们的关系是很困难的,常客根据经验 作出假设,其中最简单的加设是他们之间有线性关系:

y=+月x1++8x,+日 (8.24) 由(8.24)可知为=+1+ +xg+E,I=1,2,…,n (8.26) 其中诸1,E2,…Ew,相互独立,且服从N(0, σ2),这就是P元线性回归模型。 一、参数估计 我们先讨论如何由(8.25)取估计(8.24)中

的参数,月及σ2的问题。 设兵,月,的估计分别为,月,…, 那么我们就可以的得到一个p元线性方程: y+月石1++月x) (8.27) 称(8.27)为p元线性回归方程。对(8.25)的每一个 样本点有(8.27)可求得相应的值: :=+月x知++月, (8.28) 称(8.28)所求的得y:为回归值

+∑1月+..+∑月,=∑: ∑x1A+∑x月+.+∑x1月=∑x ∑x风+∑x月++∑号=∑x (8.29) 称(8.29)为正规方程组,其解称为,月,…, 得最小二乘估计 (8.29)可用矩阵形式简洁的表示出来。令
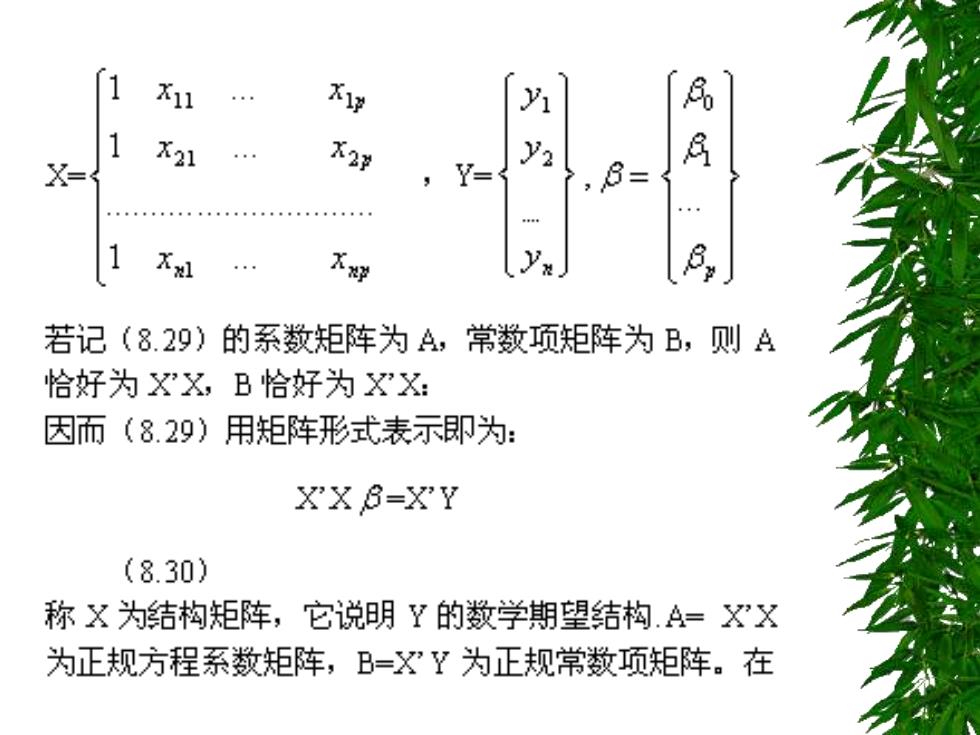
1 x11 1 X- X21 X2 y2 8= 若记(8.29)的系数矩阵为A,常数项矩阵为B,「 则A 恰好为XX,B恰好为XX: 因而(8.29)用矩阵形式表示即为: XX8-XY (8.30) 称X为结构矩阵,它说明Y的数学期望结构.A=XX 为正规方程系数矩阵,B=X'Y为正规常数项矩阵。在

回归分析中通常A1存在,这时最小二乘估计6可表 示为: 8-(XX-XY (8.31) 为求σ2的估计,先引入几个名词。称实测值”:与回归 值y:得差为残差,称 y=Y-Y=Y-X8 (8.32) 为残差向量,而称

。=20%-y)2=y'y 为剩余平方和(或残差平方和),(8.33)中各式只是它 的不同表示方法。 定理8.2 E(Se)=(n-p-1)g2 (8.34) 证明(见书399) 定理8.3 B是3的线性无偏估计,其方差协方差 矩阵为 D(6)=(X)1σ2 (8.49)

由于(8.49)表示8的方差协反差矩阵为 (X)1乘以σ2,故也称(X)1为相关矩阵。 定理8.4 Cov(Y,8)=0 (8.50) 证明(见书409) 定理8.5当YW(X6,c21)时,6与S相互独立, 且a-N(8G(Xx.等-2ag其中g 为举证X的秩。 证明(见书410)