
Department of Computer Science and Technology,Nanjing University 二部图中的匹配 离散数学课程组 南京大学计算机科学与技术系
Department of Computer Science and Technology, Nanjing University 二部图中的匹配 离散数学课程组 南京大学计算机科学与技术系

Department of Computer Science and Technology,Nanjing University 内容提要 。引言 ·二部图 ·二部图中完备匹配(Ha定理) ·二部图中的最大匹配 ·二部图中的稳定匹配 June 2016
June 2016 2 Department of Computer Science and Technology, Nanjing University 内容提要 引言 二部图 二部图中完备匹配(Hall定理) 二部图中的最大匹配 二部图中的稳定匹配
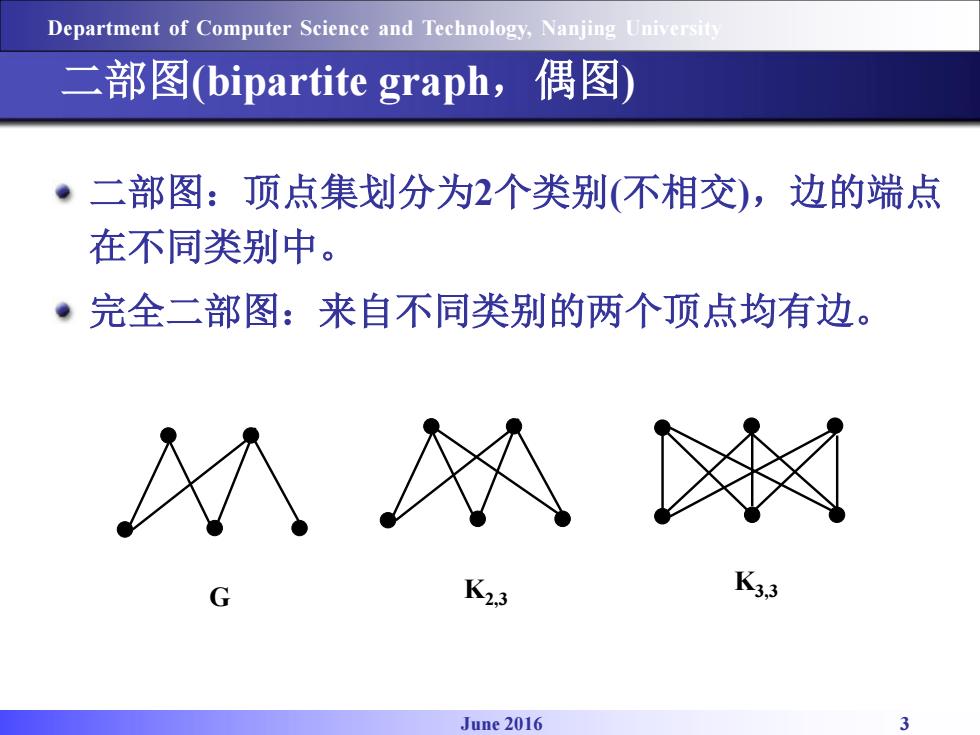
Department of Computer Science and Technology,Nanjing University 二部图(bipartite graph,偶图) ·二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 完全二部图:来自不同类别的两个顶点均有边。 州拟 K23 K33 June 2016
June 2016 3 Department of Computer Science and Technology, Nanjing University 二部图(bipartite graph,偶图) 二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 完全二部图:来自不同类别的两个顶点均有边。 K2,3 G K3,3
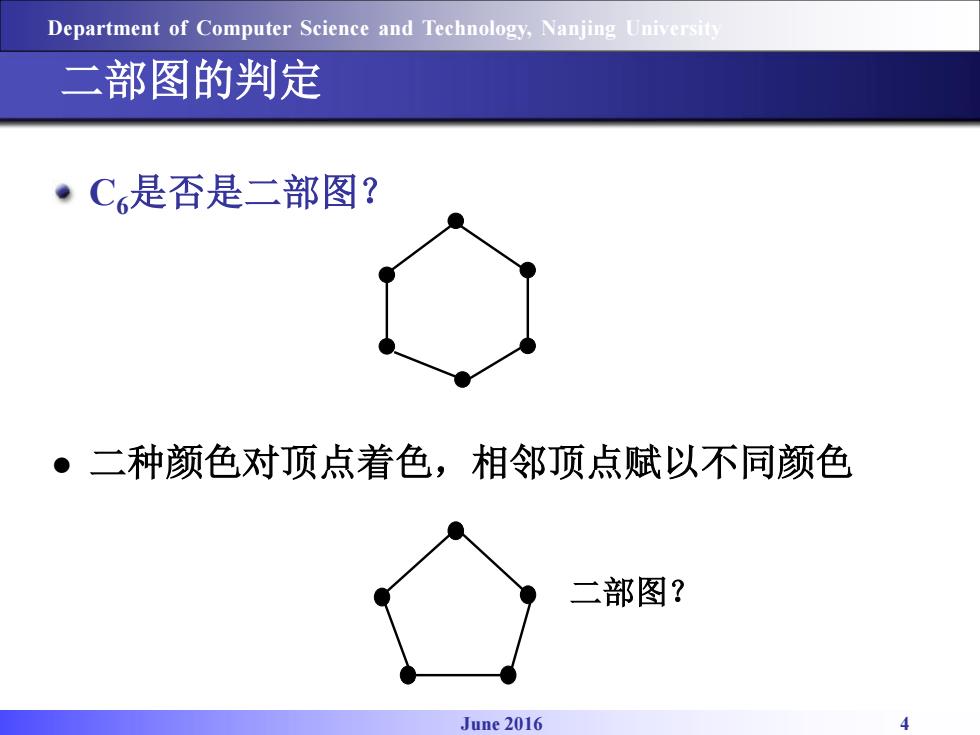
Department of Computer Science and Technology,Nanjing University 二部图的判定 ·C6是否是二部图? ·二种颜色对顶点着色,相邻顶点赋以不同颜色 二部图? June 2016
June 2016 4 Department of Computer Science and Technology, Nanjing University 二部图的判定 C6是否是二部图? 二种颜色对顶点着色,相邻顶点赋以不同颜色 二部图?

Department of Computer Science and Technology,Nanjing University 孤岛上的婚姻 ·成就最多幸福婚姻的配对方案 互不相邻的边集 June 2016 5
June 2016 5 Department of Computer Science and Technology, Nanjing University 孤岛上的婚姻 成就最多幸福婚姻的配对方案 互不相邻的边集

Department of Computer Science and Technology,Nanjing Universit 图中的匹配 ·匹配(边独立集):互不相邻的边的集合 ·M饱和点:M中各边的端点 匹配数 匹配数 β1=3 B1=4 极大匹配 完美匹配 最大匹配 ○M饱和点 ●M-饱和点 June 2016
June 2016 6 Department of Computer Science and Technology, Nanjing University 图中的匹配 匹配(边独立集):互不相邻的边的集合 M-饱和点:M中各边的端点 匹配数 1=3 匹配数 1=4 极大匹配 最大匹配 完美匹配 M-饱和点 M-饱和点
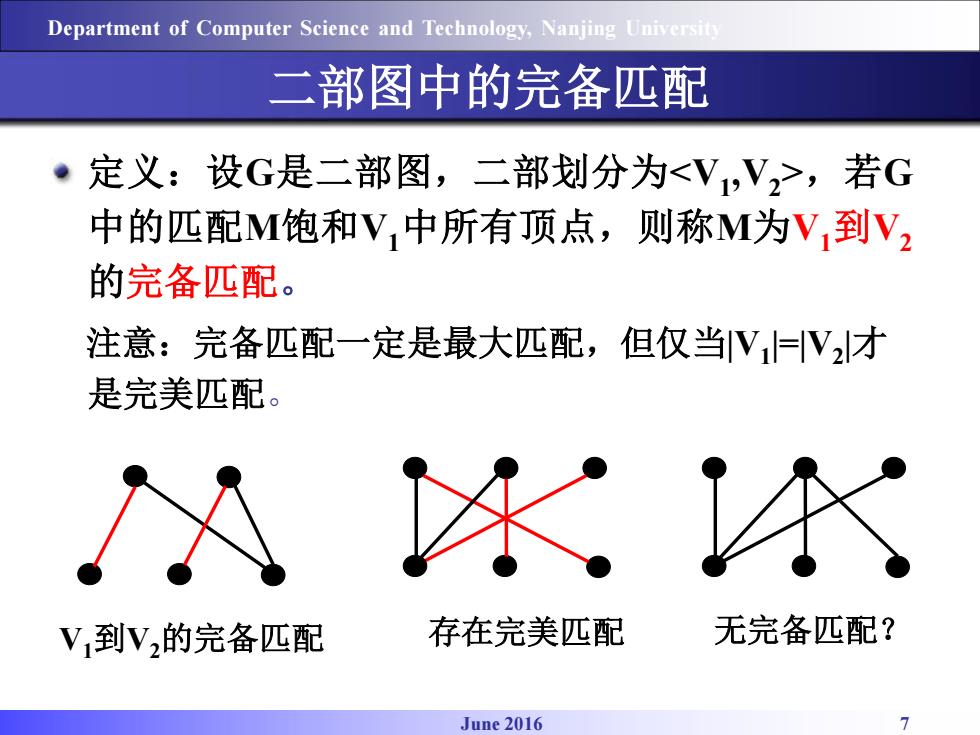
Department of Computer Science and Technology,Nanjing University 二部图中的完备匹配 定义:设G是二部图,二部划分为,若G 中的匹配M饱和V,中所有顶点,则称M为V到V2 的完备匹配。 注意:完备匹配一定是最大匹配,但仅当V=V,才 是完美匹配。 冰 V到V的完备匹配 存在完美匹配 无完备匹配? June 2016 7
June 2016 7 Department of Computer Science and Technology, Nanjing University 二部图中的完备匹配 定义:设G是二部图,二部划分为,若G 中的匹配M饱和V1中所有顶点,则称M为V1到V2 的完备匹配。 注意:完备匹配一定是最大匹配,但仅当|V1 |=|V2 |才 是完美匹配。 V1到V2的完备匹配 存在完美匹配 无完备匹配?
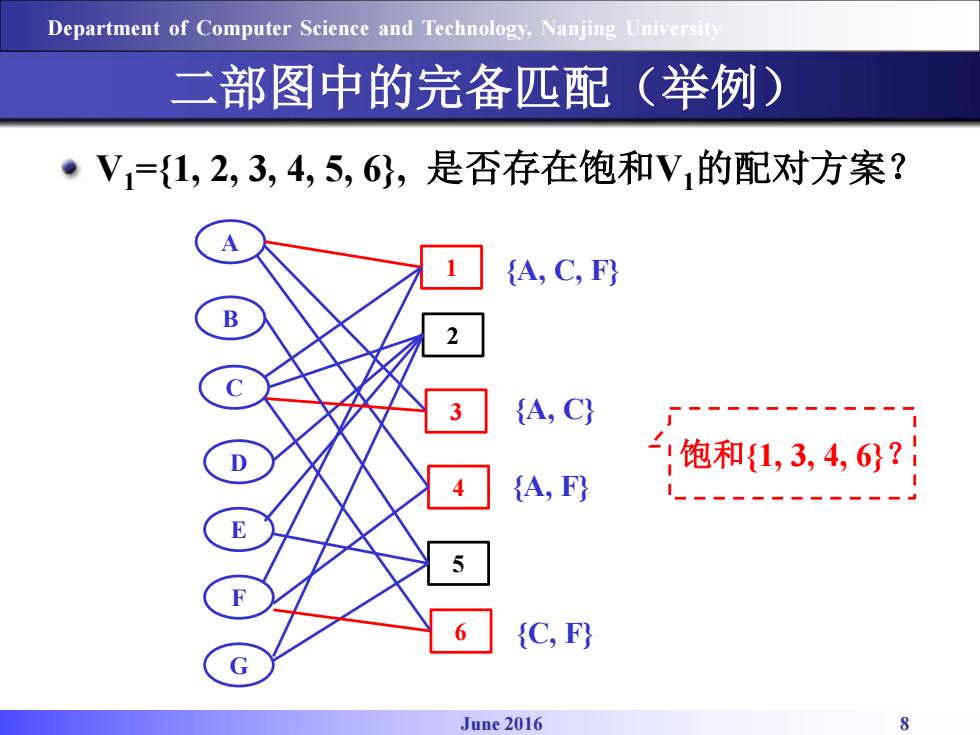
Department of Computer Science and Technology,Nanjing Universit 二部图中的完备匹配(举例) ·V={1,2,3,4,5,6,是否存在饱和V的配对方案? (A,C,F) 2 {A,C} :饱和{1,3,4,6? 4 (A,F) 5 6 (C,F) June 2016
June 2016 8 Department of Computer Science and Technology, Nanjing University 二部图中的完备匹配(举例) V1={1, 2, 3, 4, 5, 6}, 是否存在饱和V1的配对方案? A 1 B 2 C 3 D 4 E 5 F 6 G {A, C, F} {A, C} {A, F} {C, F} 饱和{1, 3, 4, 6}?

Department of Computer Science and Technology,Nanjing University Hal定理 Hall定理(1935,Marriage Theorem) 设二部图G=,则G有V到V2的完备匹配分 对于任意的AsV1,有N(A)川≥A| ·证明.必要性易证,下证充分性(使用强归纳法)。 如果V1=1,充分性命题显然成立。 假设当V1k(k≥1)时充分性命题均成立,要证:当 V=k+1时充分性命题也成立。分二种情形来证明。 ()对V的任意真子集A,N(A)川>|A (2)存在V的一个真子集A',N(A")川=|A'I June 2016 9
June 2016 9 Department of Computer Science and Technology, Nanjing University Hall定理 Hall定理(1935, Marriage Theorem) 设二部图G=, 则G有V1到V2的完备匹配 对于任意的 A V1 ,有 |N(A)| |A | 证明. 必要性易证,下证充分性(使用强归纳法)。 如果 |V1 |=1, 充分性命题显然成立。 假设当|V1 |k (k 1) 时充分性命题均成立, 要证:当 |V1 |=k+1时充分性命题也成立。分二种情形来证明。 (1)对V1的任意真子集A , |N(A)| | A | (2)存在 V1的一个真子集A', |N(A')| = | A' |

Department of Computer Science and Technology,Nanjing Universit Hall定理 ·归纳证明. 1)对V的任意真子集A,N(A)川>|A 任取一个顶点v∈V,任取w∈N(v). H=G-{V,w}是一个二部图(非空) H满足归纳假设的条件,从而 H有V1-v}到V2-{w的完备匹配. 这个匹配加上边(y,w)构成G的从 V到V,的完备匹配. June 2016
June 2016 10 Department of Computer Science and Technology, Nanjing University Hall定理 H满足归纳假设的条件, 从而 H有V1 -{v}到V2 -{w}的完备匹配. 这个匹配加上边(v, w)构成G的从 V1到V2的完备匹配. v w 归纳证明. (1)对V1的任意真子集A , |N(A)| | A | 任取一个顶点v V1 , 任取wN({v}). H=G-{v, w}是一个二部图(非空)