
《工程数学》课程教学大纲(非OBE模式) 一、课程基本信息 1.课程名称 工程数学/Engineering Mathematics 2.课程代码 33208002 3.课程类别 公共基础课程 4.课程性质 必修 5.学时/学分 56/3.5 6.先修课程 微积分 7.后续课程 无 8.适用专业 计算机、通信、光信、机械、电气、自动化、土木、环境等专升本各专业 二、课程的主要任务及目标 1.课程的主要任务 工程数学是工科各专升本专业的一门必修课,其主要内容包括行列式概念及计算、矩 阵的概念及计算、线性方程组的求解、向量组间的运算,随机事件及概率计算,一维及多 维随机变量及其分布,随机变量的数字特征等,通过本课程教学,使各专业学生掌握线性 代数和概率论与数理统计的基本理论和基本方法,使各专业学生初步掌握运用线性代数和 概率论与数理统计知识解决实际问题的能力,并为学习后续课程和进一步扩大数学知识面 奠定必要的数学基础。在讲授该门课程时,应结合应用型大学数学课程的特点和思政教育 的内涵,通过学习数学定义、公式、定理,理解数学思想,使学生对事物的方法规律有本 质的认识,培养学生的辩证唯物主义观。在立足知识的前提下,借助数学发展史、典故以 及优秀的数学家奋斗历程等,培养学生不畏艰难、坚持到底的科学态度和创新精神,同时
1 《工程数学》课程教学大纲(非 OBE 模式) 一、课程基本信息 1.课程名称 工程数学/ Engineering Mathematics 2.课程代码 33208002 3.课程类别 公共基础课程 4.课程性质 必修 5.学时/学分 56/3.5 6.先修课程 微积分 7.后续课程 无 8.适用专业 计算机、通信、光信、机械、电气、自动化、土木、环境等专升本各专业 二、课程的主要任务及目标 1.课程的主要任务 工程数学是工科各专升本专业的一门必修课,其主要内容包括行列式概念及计算、矩 阵的概念及计算、线性方程组的求解、向量组间的运算,随机事件及概率计算,一维及多 维随机变量及其分布,随机变量的数字特征等,通过本课程教学,使各专业学生掌握线性 代数和概率论与数理统计的基本理论和基本方法,使各专业学生初步掌握运用线性代数和 概率论与数理统计知识解决实际问题的能力,并为学习后续课程和进一步扩大数学知识面 奠定必要的数学基础。在讲授该门课程时,应结合应用型大学数学课程的特点和思政教育 的内涵,通过学习数学定义、公式、定理,理解数学思想,使学生对事物的方法规律有本 质的认识,培养学生的辩证唯物主义观。在立足知识的前提下,借助数学发展史、典故以 及优秀的数学家奋斗历程等,培养学生不畏艰难、坚持到底的科学态度和创新精神,同时
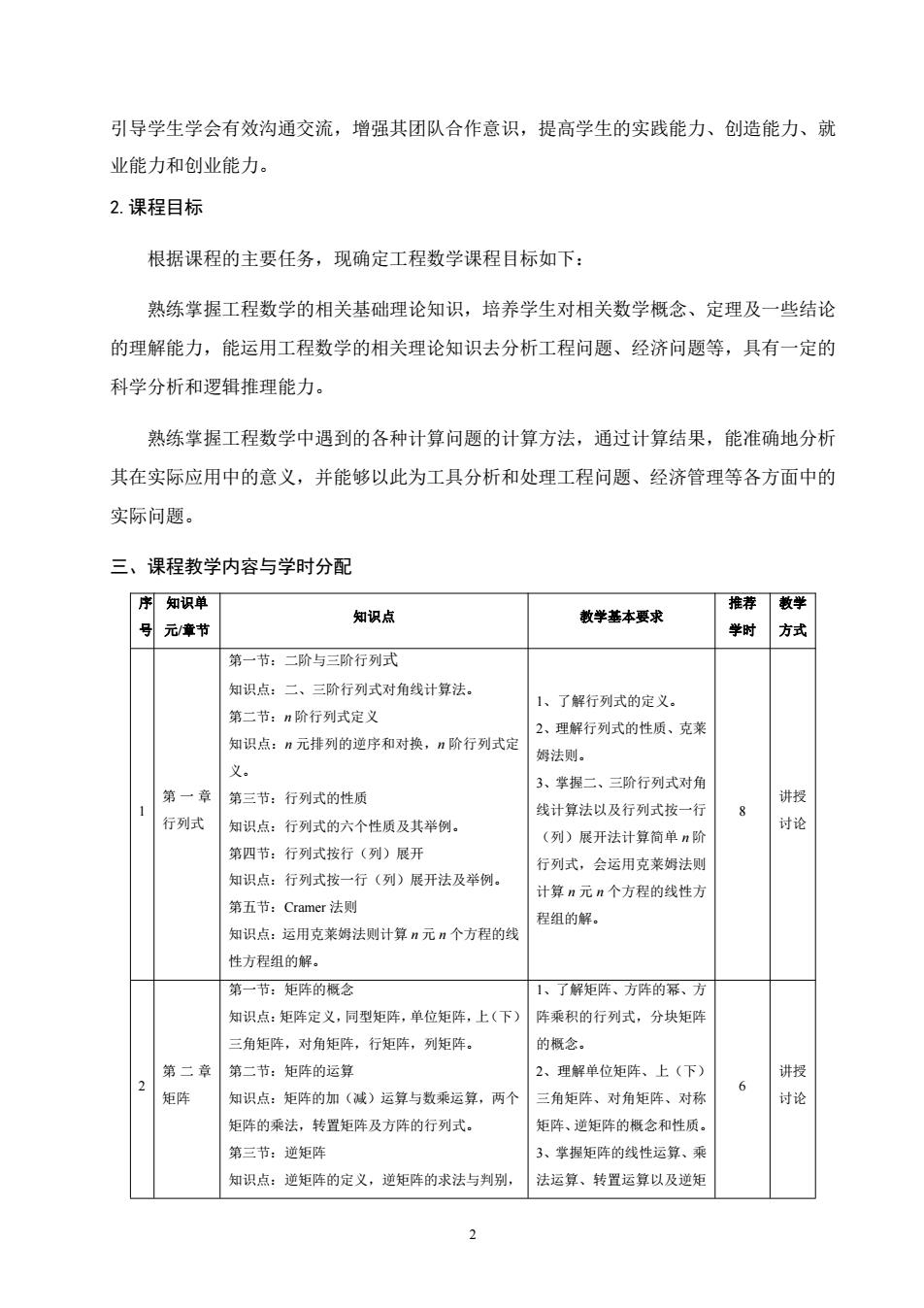
引导学生学会有效沟通交流,增强其团队合作意识,提高学生的实践能力、创造能力、就 业能力和创业能力。 2.课程目标 根据课程的主要任务,现确定工程数学课程目标如下: 熟练掌握工程数学的相关基础理论知识,培养学生对相关数学概念、定理及一些结论 的理解能力,能运用工程数学的相关理论知识去分析工程问题、经济问题等,具有一定的 科学分析和逻辑推理能力。 熟练掌握工程数学中遇到的各种计算问题的计算方法,通过计算结果,能准确地分析 其在实际应用中的意义,并能够以此为工具分析和处理工程问题、经济管理等各方面中的 实际问题。 三、课程教学内容与学时分配 序知识单 推荐散学 号元康节 知识点 教学善本要求 学时 方式 第一节一阶与三阶行列式 知识点:二,三阶行列式对角线计算法 1、了解行列式的定义, 第二节:n阶行列式定义 2、理解行列式的性质、克莱 知识点:n元排列的逆序和对换,n阶行列式定 姆法则。 3、掌提二、三阶行列式对 第三节:行列式的性质 讲授 线计算法以及行列式按一行 行列式知识点:行列式的六个性质及其举例。 讨论 (列)展开法计算简单n阶 第四节:行列式按行(列)展开 行列式,会运用克莱姆法圆 知识点:行列式技一行(列)》展开法及举例。 计算月元n个方程的线性方 第五节:Cramer法则 程组的解 知识点:运用克莱组法侧计算财元月个方程的 性方程组的解。 第一节:矩阵的树今 1、了解钜陈、方阵的活、方 知识点:矩阵定义,同型矩阵,单位矩阵,上(下) 阵乘积的行列式,分块矩阵 三角矩库,对角矩阵,行矩阵,列矩阵。 的概念。 第二章第二节:矩阵的运算 2、理解单位矩阵、上(下) 矩阵 知识点:矩阵的加(减)运算与数乘运算,两个 三角矩阵、对角矩阵、对称 6 讲授 讨 矩阵的乘法,转置矩阵及方阵的行列式。 短阵、道矩阵的概会和性质 第三节:逆矩阵 3、掌握矩阵的线性运算、乘 知识点:逆矩阵的定义,道矩阵的求法与判别 法运算、转置运算以及逆矩
2 引导学生学会有效沟通交流,增强其团队合作意识,提高学生的实践能力、创造能力、就 业能力和创业能力。 2.课程目标 根据课程的主要任务,现确定工程数学课程目标如下: 熟练掌握工程数学的相关基础理论知识,培养学生对相关数学概念、定理及一些结论 的理解能力,能运用工程数学的相关理论知识去分析工程问题、经济问题等,具有一定的 科学分析和逻辑推理能力。 熟练掌握工程数学中遇到的各种计算问题的计算方法,通过计算结果,能准确地分析 其在实际应用中的意义,并能够以此为工具分析和处理工程问题、经济管理等各方面中的 实际问题。 三、课程教学内容与学时分配 序 号 知识单 元/章节 知识点 教学基本要求 推荐 学时 教学 方式 1 第 一 章 行列式 第一节:二阶与三阶行列式 知识点:二、三阶行列式对角线计算法。 第二节:n 阶行列式定义 知识点:n 元排列的逆序和对换,n 阶行列式定 义。 第三节:行列式的性质 知识点:行列式的六个性质及其举例。 第四节:行列式按行(列)展开 知识点:行列式按一行(列)展开法及举例。 第五节:Cramer 法则 知识点:运用克莱姆法则计算 n 元 n 个方程的线 性方程组的解。 1、了解行列式的定义。 2、理解行列式的性质、克莱 姆法则。 3、掌握二、三阶行列式对角 线计算法以及行列式按一行 (列)展开法计算简单 n 阶 行列式,会运用克莱姆法则 计算 n 元 n 个方程的线性方 程组的解。 8 讲授 讨论 2 第 二 章 矩阵 第一节:矩阵的概念 知识点:矩阵定义,同型矩阵,单位矩阵,上(下) 三角矩阵,对角矩阵,行矩阵,列矩阵。 第二节:矩阵的运算 知识点:矩阵的加(减)运算与数乘运算,两个 矩阵的乘法,转置矩阵及方阵的行列式。 第三节:逆矩阵 知识点:逆矩阵的定义,逆矩阵的求法与判别, 1、了解矩阵、方阵的幂、方 阵乘积的行列式,分块矩阵 的概念。 2、理解单位矩阵、上(下) 三角矩阵、对角矩阵、对称 矩阵、逆矩阵的概念和性质。 3、掌握矩阵的线性运算、乘 法运算、转置运算以及逆矩 6 讲授 讨论
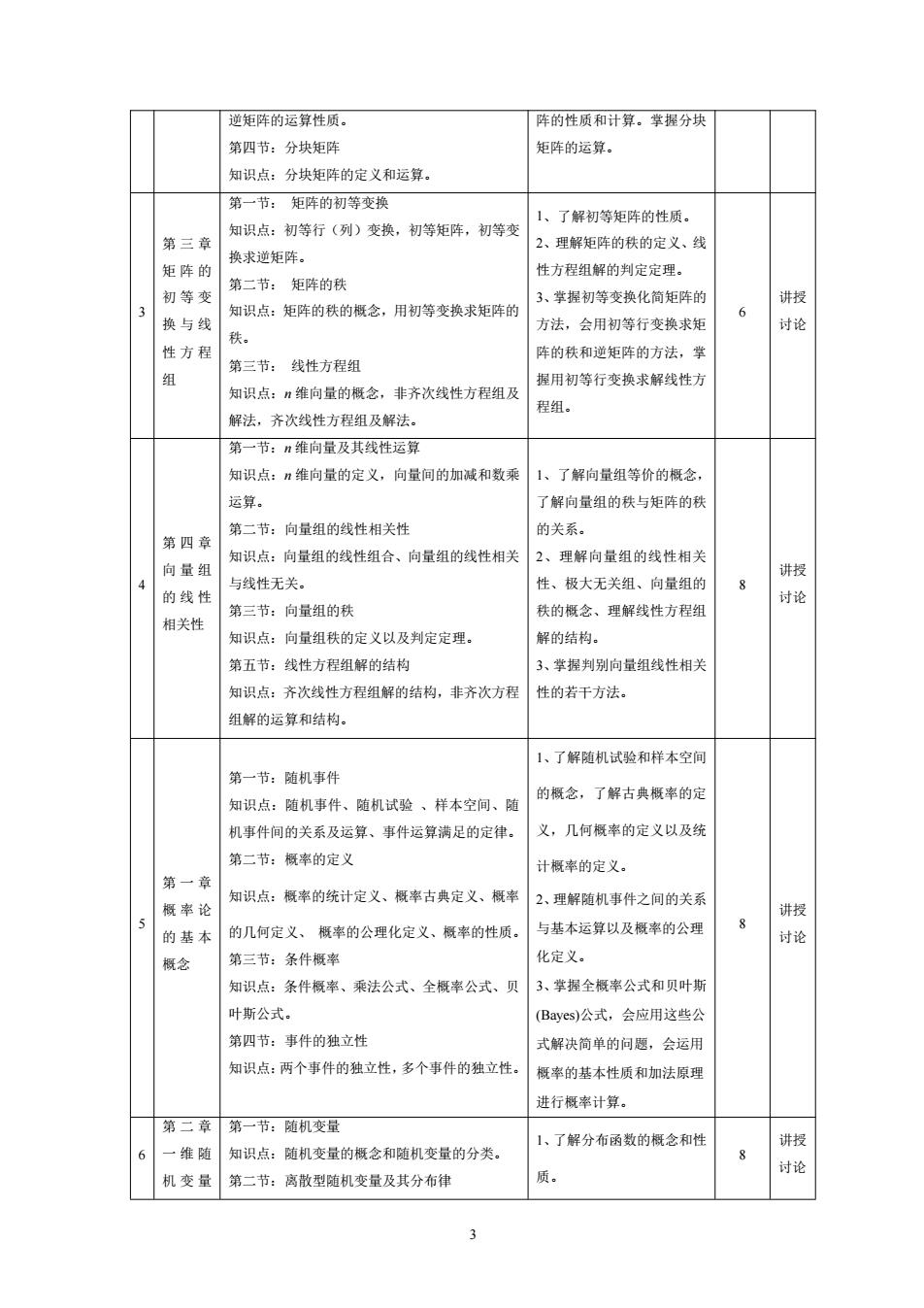
逆矩阵的运算性质, 阵的性质和计算,掌握分块 第四节:分块矩阵 矩阵的运算。 知识点:分块矩阵的定义和运算。 第一节。矩阵的初等变换 知识点:初等行(列)变换,初等矩阵,初等变 1、了解初等矩阵的性质。 第三章 2、理解矩阵的秩的定义、线 换求逆矩阵。 钜的 性方程组解的判定定理, 第二节:矩阵的 初等变 知识点:矩阵的秩的概念,用初等变换求矩阵的 3、掌握初等变换化简矩阵的 讲授 换与线 方法,会用初等行变换求矩 6 讨论 陆 性方程 阵的秩和逆矩阵的方法,掌 第三节:线性方程组 捉用初等行变换求解线性方 知识点:维向量的概念,非齐次线性方程组及 程组 解法,齐次线性方程组及解法。 第一节:月维向量及其线性运算 知识点:n维向量的定义,向量间的加减和数乘 1、了解向量组等价的概念, 云官。 了解向量组的秩与矩阵的积 第二节:向量组的线性相关性 第四章 的类系。 2、理解向量组的线性相关 向量组 知识点:向量组的线性组合、向量组的线性相关 与线性无关。 性、极大无关组、向量组的 的线性 第三节:向量组的秩 秩的概念、理解线性方程组 讨论 相关性 知识点:向量组秩的定义以及判定定理 解的结构。 第五节:线性方程组解的结构 3、掌握判别向量组线性相关 知识点:齐次线性方程组解的结构,非齐次方稻 性的若干方法。 组解的运算和结构。 1、了解随机试验和样本空间 第一节,随机电件 知识点:随机事件、随机试验、样本空、随 的概念,了解古典概率的庭 机事件间的关系及运算、事件运算满足的定律。 义,几何概率的定义以及统 第二节:概率的定义 第一 计概率的定义。 知识点:概率的统计定义、概率古典定义、概率 2、理解随机事件之间的关系 概事论 讲授 的基本的几何定义、概率的公理化定义、概率的性质。 与基本运算以及概率的公理 讨论 概念 第三节:条件概率 化定义。 知识点:条件概率、乘法公式、全概率公式、贝 3,掌操全概率公式和贝叶抑 叶断公式。 Baycs)公式,会应用这些公 第四节:事件的独立性 式解决简单的问题。会运用 知识点:两个事件的独立性,多个事件的独立性 概率的基本性质和加法原理 进行概家计算, 第 第一节:随机变量 1、了解分布函数的概念和性 讲授 一维随知识点:随机变量的概念和随机变量的分类。 讨论 机变量 第二节:离散型随机变量及其分布律
3 逆矩阵的运算性质。 第四节:分块矩阵 知识点:分块矩阵的定义和运算。 阵的性质和计算。掌握分块 矩阵的运算。 3 第 三 章 矩 阵 的 初 等 变 换 与 线 性 方 程 组 第一节: 矩阵的初等变换 知识点:初等行(列)变换,初等矩阵,初等变 换求逆矩阵。 第二节: 矩阵的秩 知识点:矩阵的秩的概念,用初等变换求矩阵的 秩。 第三节: 线性方程组 知识点:n 维向量的概念,非齐次线性方程组及 解法,齐次线性方程组及解法。 1、了解初等矩阵的性质。 2、理解矩阵的秩的定义、线 性方程组解的判定定理。 3、掌握初等变换化简矩阵的 方法,会用初等行变换求矩 阵的秩和逆矩阵的方法,掌 握用初等行变换求解线性方 程组。 6 讲授 讨论 4 第 四 章 向 量 组 的 线 性 相关性 第一节:n 维向量及其线性运算 知识点:n 维向量的定义,向量间的加减和数乘 运算。 第二节:向量组的线性相关性 知识点:向量组的线性组合、向量组的线性相关 与线性无关。 第三节:向量组的秩 知识点:向量组秩的定义以及判定定理。 第五节:线性方程组解的结构 知识点:齐次线性方程组解的结构,非齐次方程 组解的运算和结构。 1、了解向量组等价的概念, 了解向量组的秩与矩阵的秩 的关系。 2、理解向量组的线性相关 性、极大无关组、向量组的 秩的概念、理解线性方程组 解的结构。 3、掌握判别向量组线性相关 性的若干方法。 8 讲授 讨论 5 第 一 章 概 率 论 的 基 本 概念 第一节:随机事件 知识点:随机事件、随机试验 、样本空间、随 机事件间的关系及运算、事件运算满足的定律。 第二节:概率的定义 知识点:概率的统计定义、概率古典定义、概率 的几何定义、 概率的公理化定义、概率的性质。 第三节:条件概率 知识点:条件概率、乘法公式、全概率公式、贝 叶斯公式。 第四节:事件的独立性 知识点:两个事件的独立性,多个事件的独立性。 1、了解随机试验和样本空间 的概念,了解古典概率的定 义,几何概率的定义以及统 计概率的定义。 2、理解随机事件之间的关系 与基本运算以及概率的公理 化定义。 3、掌握全概率公式和贝叶斯 (Bayes)公式,会应用这些公 式解决简单的问题,会运用 概率的基本性质和加法原理 进行概率计算。 8 讲授 讨论 6 第 二 章 一 维 随 机 变 量 第一节:随机变量 知识点:随机变量的概念和随机变量的分类。 第二节:离散型随机变量及其分布律 1、了解分布函数的概念和性 质。 8 讲授 讨论
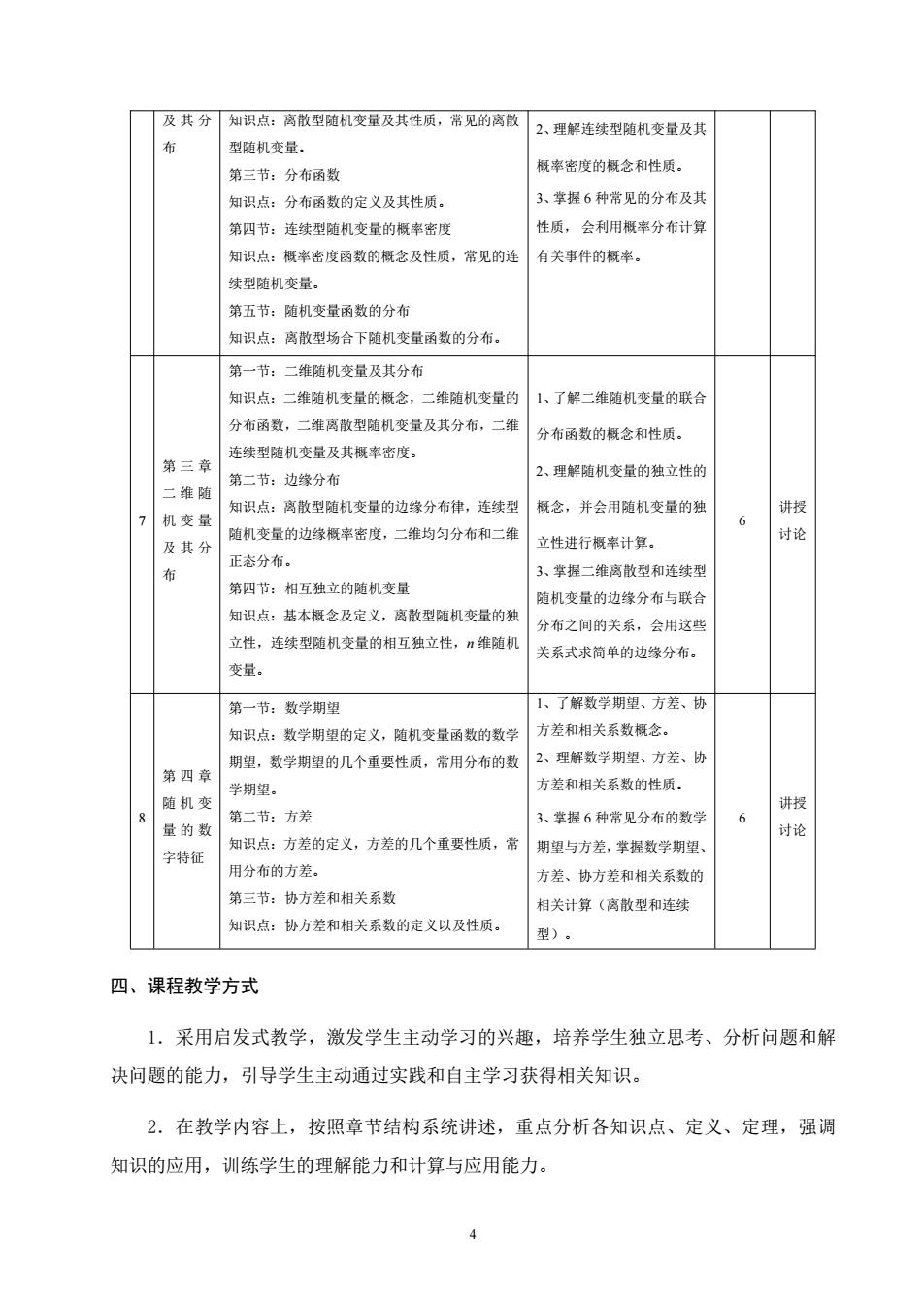
及其分知识点:高散随机变量及其性质,常见的离散2、理解连铁型随机变量及其 型随机变量。 第三节:分布函数 概率密度的概念和性质。 知识点:分布函数的定义及其性质。 3、拿握6种常见的分布及其 第四节:连续型随机变量的概率密肉 性质,会利用概率分布计算 知识点:概率密度函数的概念及性质,常见的连有关事件的概率。 续型随机变量。 第五节:随机变量函数的分布 知识点:离散型场合下随机变量函数的分布。 第一节:一维随机变量及其分布 知识点:二维随机变量的概念,二维随机变量的 1、了解二维随机变量的联合 分布函数,二维离散型随机变量及其分布,二维雄 分布函数的概念和性质。 连续型随机变量及其概率密度。 第三章 第一节。边炎分有 2、理解随机变量的独立性的 二维随 知识点:离散型随机变量的边缘分布律,连续 机变量 概念,并会用随机变量的独 随机变量的边缘概率密度,二一维均匀分布和二维 6 讲授 立性进行概常计算。 讨论 及其分 正本分有。 布 ;、堂操一维离散型和车统形 第四节:相互独立的随机变量 随机变量的边缘分布与联合 知识点:基本概今及定义,离散型随机李量的和 分布之间的关系,会用这此 立性,连续型随机变量的相互独立性,厅雏随机 关系式求简单的边缘分布。 变量, 第一节:数学期年 、了解数学期望、方差、协 知识点:数学期望的定义,随机变量函数的数学 方差和相关系数概念。 期望,数学期望的几个重要性质,常用分布的数 2、理解数学期望、方差、协 第四章 学期望。 方差和相关系数的性质 量的数第二:方花 随机变 、幸握6种常见分布的数学 6 讲授 讨论 知识点:方差的定义,方差的几个重要性质,常 期望与方差,掌程数学期望 字特征 用分布的方差。 方差、协方差和相关系数的 第三节:协方差和相关系数 相关计算(离敢型和连续 知识点:协方差和相关系数的定义以及性质。 型). 四、课程教学方式 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解 决问题的能力,引导学生主动通过实践和自主学习获得相关知识。 2.在教学内容上,按照章节结构系统讲述,重点分析各知识点、定义、定理,强调 知识的应用,训练学生的理解能力和计算与应用能力。 4
4 及 其 分 布 知识点:离散型随机变量及其性质,常见的离散 型随机变量。 第三节:分布函数 知识点:分布函数的定义及其性质。 第四节:连续型随机变量的概率密度 知识点:概率密度函数的概念及性质,常见的连 续型随机变量。 第五节:随机变量函数的分布 知识点:离散型场合下随机变量函数的分布。 2、理解连续型随机变量及其 概率密度的概念和性质。 3、掌握 6 种常见的分布及其 性质, 会利用概率分布计算 有关事件的概率。 7 第 三 章 二 维 随 机 变 量 及 其 分 布 第一节:二维随机变量及其分布 知识点:二维随机变量的概念,二维随机变量的 分布函数,二维离散型随机变量及其分布,二维 连续型随机变量及其概率密度。 第二节:边缘分布 知识点:离散型随机变量的边缘分布律,连续型 随机变量的边缘概率密度,二维均匀分布和二维 正态分布。 第四节:相互独立的随机变量 知识点:基本概念及定义,离散型随机变量的独 立性,连续型随机变量的相互独立性,n 维随机 变量。 1、了解二维随机变量的联合 分布函数的概念和性质。 2、理解随机变量的独立性的 概念,并会用随机变量的独 立性进行概率计算。 3、掌握二维离散型和连续型 随机变量的边缘分布与联合 分布之间的关系,会用这些 关系式求简单的边缘分布。 6 讲授 讨论 8 第 四 章 随 机 变 量 的 数 字特征 第一节:数学期望 知识点:数学期望的定义,随机变量函数的数学 期望,数学期望的几个重要性质,常用分布的数 学期望。 第二节:方差 知识点:方差的定义,方差的几个重要性质,常 用分布的方差。 第三节:协方差和相关系数 知识点:协方差和相关系数的定义以及性质。 1、了解数学期望、方差、协 方差和相关系数概念。 2、理解数学期望、方差、协 方差和相关系数的性质。 3、掌握 6 种常见分布的数学 期望与方差,掌握数学期望、 方差、协方差和相关系数的 相关计算(离散型和连续 型)。 6 讲授 讨论 四、课程教学方式 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解 决问题的能力,引导学生主动通过实践和自主学习获得相关知识。 2.在教学内容上,按照章节结构系统讲述,重点分析各知识点、定义、定理,强调 知识的应用,训练学生的理解能力和计算与应用能力

3.在教学过程中采取多媒体教学与传统板书、教具教学相结合的教学方式,提高课 堂教学信息量,增强教学的直观性。重视课后的习题练习,不定期讲解作业。 4.课内讨论和课外答疑相结合,线上线下相结合,灵活使用现代教学技术和手段, 如超星信息化手段。 五、课程的考核环节及课程目标达成度评价方式 1.课程考核环节描述 本课程的考核方式为考试,闭卷。课程的考核以考核学生能力培养目标的达成为主要 目的,以检查学生对各知识点的掌握程度和应用能力为重要内容,包括平时考核和期末考 核两个环节,平时考核包括课后作业和到课率,期末考核为期末考试。相应地,课程总评 成绩由平时考核成绩和期末考核成绩两部分加权而成,平时成绩、考试成绩及总评成绩均 为百分制,在总评成绩中,平时成绩、考试成绩所占的权重分别为、2,其中1、2根 据学校相关规定分别定为0.2和0.8。 2.各考核环节所占分值比例及考核细则 各考核环节所占分值比例及考核细则如下。 课程成绩构成及比例 考核环节 考核/评价细则 平时成绩100分,占总评成绩 主要考核学生基本知识点的掌握情况,成绩以百分计,乘以其在总 考勤 平时成绩的比例为 平成绩中所占的比例,后相加计入课程总评成镜。检测方式为:考 作业 =0.2 与作业 (1)卷面成绩100分,以卷面成绩乘以其在总评成绩中所占的 期末考试100分,占总评成绩 例计入课程总评成绩。 比例为 期末考试 (2)主要考核各个章节的概念理解及计算分析能力,考试题型为: 7=0.8 选择题、填空题、计算题、证明题。 六、建议教材及教学参考书 (一)推荐教材
5 3.在教学过程中采取多媒体教学与传统板书、教具教学相结合的教学方式,提高课 堂教学信息量,增强教学的直观性。重视课后的习题练习,不定期讲解作业。 4.课内讨论和课外答疑相结合,线上线下相结合,灵活使用现代教学技术和手段, 如超星信息化手段。 五、课程的考核环节及课程目标达成度评价方式 1.课程考核环节描述 本课程的考核方式为考试,闭卷。课程的考核以考核学生能力培养目标的达成为主要 目的,以检查学生对各知识点的掌握程度和应用能力为重要内容,包括平时考核和期末考 核两个环节,平时考核包括课后作业和到课率,期末考核为期末考试。相应地,课程总评 成绩由平时考核成绩和期末考核成绩两部分加权而成,平时成绩、考试成绩及总评成绩均 为百分制,在总评成绩中,平时成绩、考试成绩所占的权重分别为、,其中、根 据学校相关规定分别定为 0.2 和 0.8。 2.各考核环节所占分值比例及考核细则 各考核环节所占分值比例及考核细则如下。 课程成绩构成及比例 考核环节 考核/评价细则 平时成绩 平时成绩分,占总评成绩 的比例为 考勤 作业 主要考核学生基本知识点的掌握情况。成绩以百分计,乘以其在总 评成绩中所占的比例后相加计入课程总评成绩。检测方式为:考 勤与作业。 考试成绩 期末考试分,占总评成绩 的比例为 期末考试 (1)卷面成绩 100 分,以卷面成绩乘以其在总评成绩中所占的比 例计入课程总评成绩。 (2)主要考核各个章节的概念理解及计算分析能力。考试题型为: 选择题、填空题、计算题、证明题。 六、建议教材及教学参考书 (一)推荐教材

[1]朱祥和主编.线性代数及应用.武汉:华中科技大学出版社,20167. [2]龙松主编.概率统计及应用.武汉:华中科技大学出版社,2016.7 (二)主要参考资料 [1]朱祥和主编.线性代数及应用学习指导.武汉:华中科技大学出版社,2016.8. [2]同济大学编著.线性代数(第六版).北京:高等教育出版社,2014.6. [3]程迪祥等编著.线性代数(第2版).北京:清华大学出版社,2013.11. [4]龙松主编.概率统计及应用学习指导.武汉:华中科技大学出版社,2017.1. [5]盛骤等编著.概率论与数理统计(第五版),北京:高等教育出版社,2020.11 [6]张帼奋等编著.概率论与数理统计.北京:高等教育出版社,2017.10. [7]同济大学数学系编著.概率论与数理统计.北京:人民邮电出版社,2017.3. 七、其他说明 无 执笔人(签字): 年月日 审核人(签字): 年月日
6 [1] 朱祥和主编.线性代数及应用.武汉:华中科技大学出版社,2016.7. [2] 龙 松主编.概率统计及应用.武汉:华中科技大学出版社,2016.7. (二)主要参考资料 [1] 朱祥和主编.线性代数及应用学习指导.武汉:华中科技大学出版社,2016.8. [2] 同济大学编著.线性代数(第六版).北京:高等教育出版社,2014.6. [3] 程迪祥等编著.线性代数(第 2 版).北京:清华大学出版社,2013.11. [4] 龙松主编.概率统计及应用学习指导.武汉:华中科技大学出版社,2017.1. [5] 盛骤等编著.概率论与数理统计(第五版).北京:高等教育出版社,2020.11. [6] 张帼奋等编著.概率论与数理统计.北京:高等教育出版社,2017.10. [7] 同济大学数学系编著.概率论与数理统计.北京:人民邮电出版社,2017.3. 七、其他说明 无 执笔人(签字): 年 月 日 审核人(签字): 年 月 日