
最短通路问题 离散数学一图论初步 南京大学计算机科学与技术系
最短通路问题 离散数学─图论初步 南京大学计算机科学与技术系

内容提要 ·引言 ●Dijkstra.算法 ·旅行商问题(TSP)
内容提要 引言 Dijkstra算法 旅行商问题(TSP)

带权图与最短通路问题 带权图:三元组(V,E,,(V,E)是图,W是从E到 非负实数集的一个函数。We)表示边e的权。 ·一条通路上所有边的权的和称为该通路的长度。 ·两点之间长度最小的通路称为两点之间的最短通路, 不一定是唯一的。 ·单源点最短路问题 给定带权图G(V,E,W并指定一个源点,确定该源 点到图中其它任一顶点的最短路(长度和路径)
带权图与最短通路问题 带权图:三元组 (V, E, W),(V, E)是图,W是从E到 非负实数集的一个函数。W(e)表示边e的权。 一条通路上所有边的权的和称为该通路的长度。 两点之间长度最小的通路称为两点之间的最短通路, 不一定是唯一的。 单源点最短路问题 给定带权图 G(V, E, W)并指定一个源点,确定该源 点到图中其它任一顶点的最短路(长度和路径)

Dijkstra:最短路径的算法思想(1959) ●】 源点s到顶点v的最短路径若为suy,则s.u是s到u 的最短路径。 ● (-1)条最短路径按照其长度的非减次序求得,设它 们的相应端点分别为u,u1,最短路径长度记为 d(s,),i=1,n-1. ·假设前条最短路径已知,第(+1)条最短路径长度: d(s,ui+1)=minfd(s,u)+W(u,ui+1)j=1,...i}
Dijkstra最短路径的算法思想(1959) 源点s到顶点v的最短路径若为s…uv, 则s…u是s到u 的最短路径。 (n-1)条最短路径按照其长度的非减次序求得,设它 们的相应端点分别为u1 , …un-1,最短路径长度记为 d(s, ui ) , i=1,…n-1. 假设前i条最短路径已知,第(i+1)条最短路径长度: d(s, ui+1 )=min{d(s, uj ) +W(uj , ui+1 )| j=1,…i}

求最短路径的Dijkstra算法 ●输入:连通带权图G,Vc=n,指定顶点s∈Vc ●输出:每个顶点v的标注L(y),W),其中: ·L()即从s到的最短路径长度(目前可得的) ●u是该路径上v前一个顶点
求最短路径的Dijkstra算法 输入:连通带权图G,|VG |=n, 指定顶点sVG 输出:每个顶点v的标注(L(v), u), 其中: L(v)即从s到v的最短路径长度(目前可得的) u是该路径上v前一个顶点
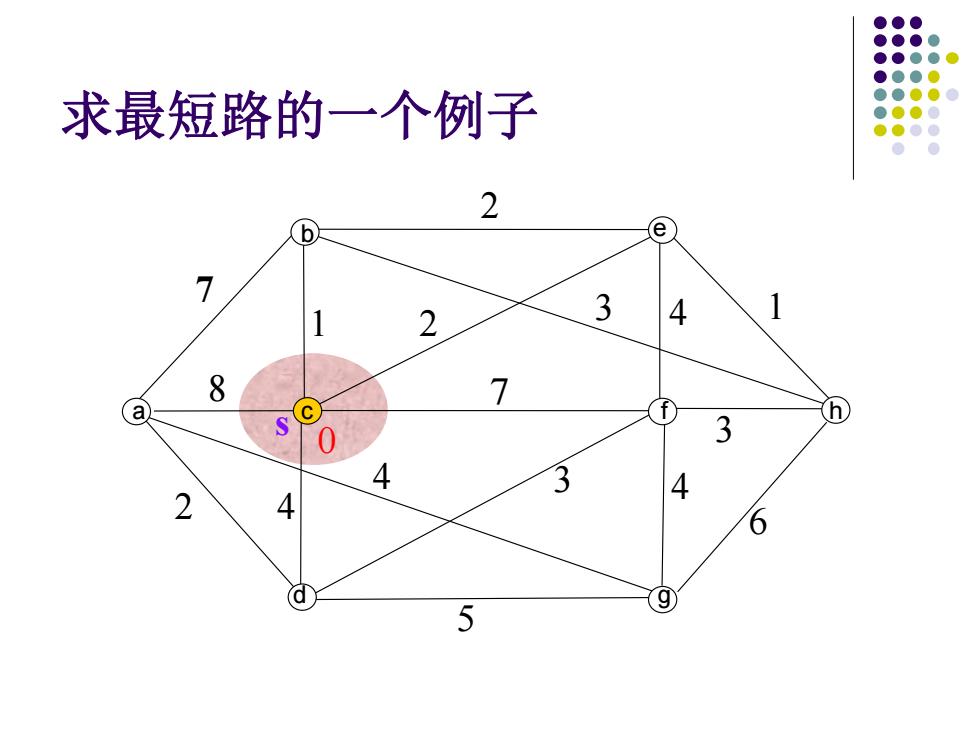
求最短路的一个例子 2 6 2 3 4 8 7 a h 0 3 3 4 2 4 o d 5 9
求最短路的一个例子 s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 b a c d e f g h

● 求最短路的一个例子 U1 2 2,C 2 3 4 8 7 h 8, 1 0 3 3 4 2 4 d ⑨ 4,C 5
求最短路的一个例子 s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U1 b a c d e f g h

●● ● ● S1 19 2 2,9 U2 e 7 2 3 4 8 7 c 190 4,b a h 8 0 3 4 3 4 2 4 6 d 9 4,c 5
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U2 b a cd efg h 4,b S1
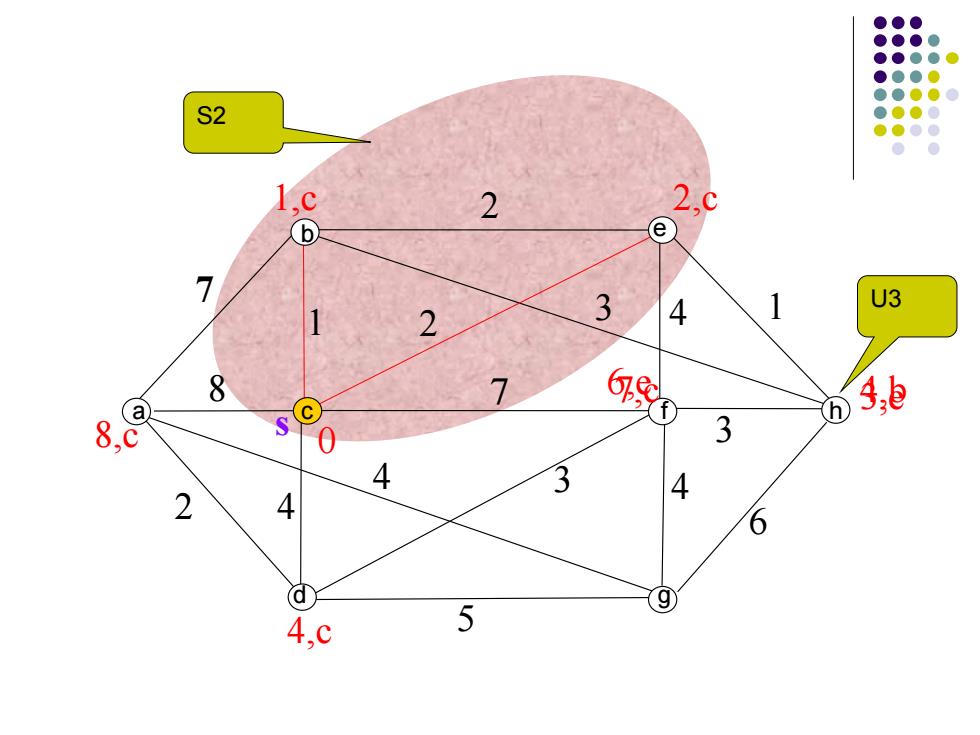
● ● ● ● S2 ● ,C 2 2,C e 1 2 3 4 U3 8 7 e a h 8 3 4 3 4 2 4 6 d ⑨ 4,C 5
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U3 b a cd efg h 4,b S2 3,e 6,e

● S3 ,C 2 2,C b e 7 1 2 3 4 8 a 6 8 0 3 3 e 4 3 4 2 4 6 a 9 4,C 5 9,h U4
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 6,e 4,c b a c d e f g h U4 3,e 9,h S3