
实验1 MATLAB入门 参考答案 1.输入三角形三条边长,求面积,编写一个函数实现。 function area ]=TriArea(ab.c) %翰入b,表示三角形的三条边长 %输出:表示出的三角形面积: %方法:海伦公式。 ifa=b+c |b>=a+clc>=a+b disp(警告:不能构成三角形!方 return end s-(a+b+cY2. aea=sqr(s*(s-a)产(-b产(-c end S1=TriArea(3,45)%直角三角形 S2=TriArea(10,10,10)%等边三角形 S1= 6 S2= 43.3013 2.绘出李萨如图形,要求在同一个图形窗口的6个子窗口中依次输出相位差0-0,4,3玩2, 3π4,π及这五个图形的叠加图形。 cle.clear.close all %A1、A2控制频率,如果恰好为倍数,图像比较好看,互质会很密。 %C1、C2控制振幅,自定义设置没有特别的地方。 %B是一组相位差 T=00.01pi; A1=3, A2=6: C1=4 C2=3 B=[0 pi/4 3*pi/2 3*pi/4 pi]: for i=1:5
实验 1 MATLAB 入门 参考答案 1. 输入三角形三条边长,求面积,编写一个函数实现。 function [ area ] = TriArea( a,b,c ) % 输入a,b,c表示三角形的三条边长; % 输出:area表示输出的三角形面积; % 方法:海伦公式。 if a=b+c | b>=a+c | c>=a+b disp('警告:不能构成三角形!'); return end s=(a+b+c)/2; area=sqrt(s*(s-a)*(s-b)*(s-c)); end ------------------------------------------------ S1=TriArea( 3,4,5 )%直角三角形 S2=TriArea( 10,10,10 )%等边三角形 S1 = 6 S2 = 43.3013 2. 绘出李萨如图形,要求在同一个图形窗口的6个子窗口中依次输出相位差φ=0,π/4, 3π/2, 3π/4, π及这五个图形的叠加图形。 clc,clear,close all %A1、A2控制频率,如果恰好为倍数,图像比较好看,互质会很密。 %C1、C2控制振幅,自定义设置没有特别的地方。 %B是一组相位差 T=0:0.01:pi; A1=3; A2=6; C1=4; C2=3; B=[0 pi/4 3*pi/2 3*pi/4 pi]; for i=1:5
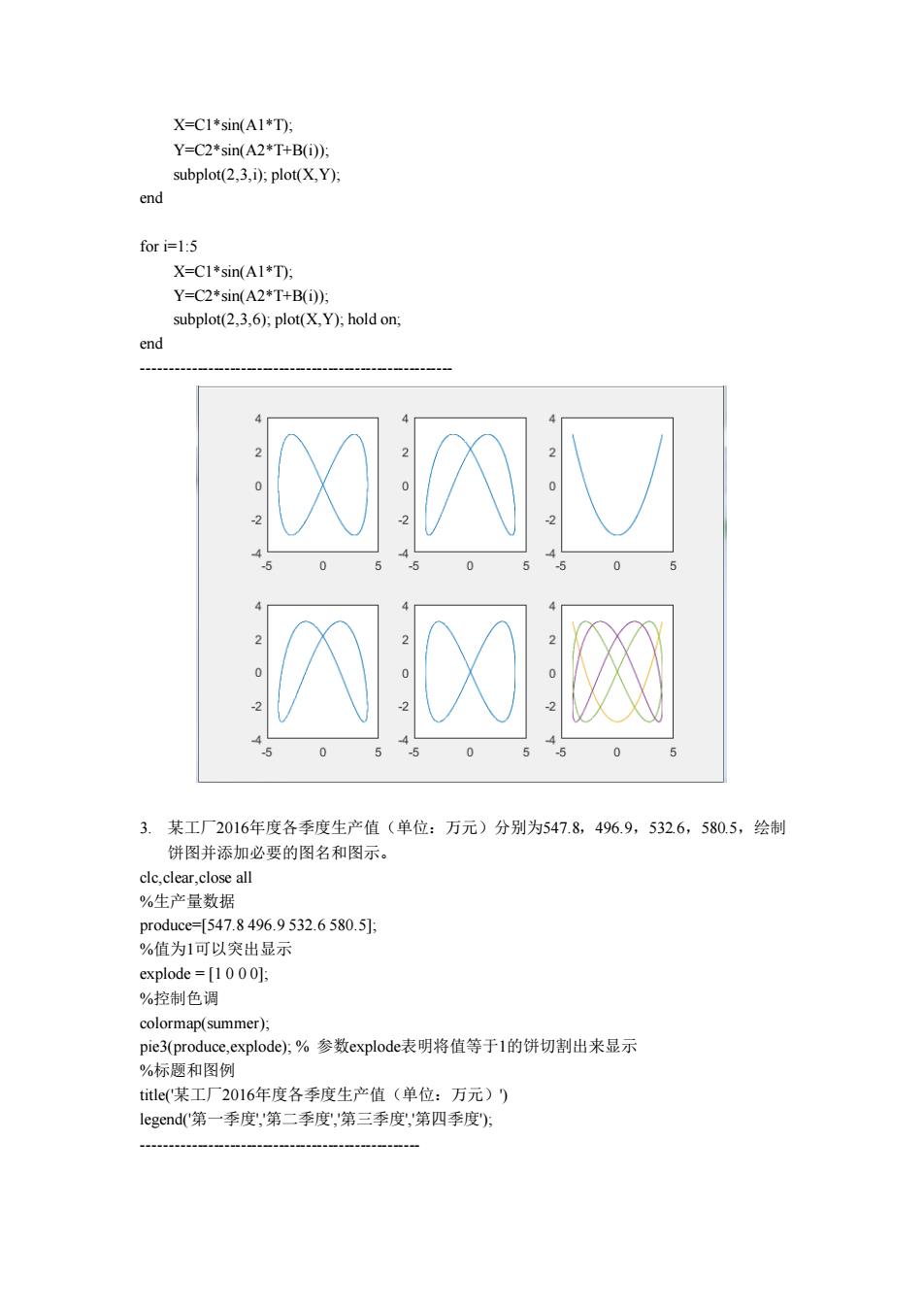
X=C1*sin(A1*T) Y=C2*sin(A2+T+B(i)) subplot(2.3.i):plot(X.Y) end for i=1:5 X=CI*sin(AI*T): Y=C2*sin(A2+T+B(i)): subplot(2.3.6):plot(X.Y):hold on: end kniv 四风题 3.某工厂2016年度各季度生产值(单位:万元)分别为547.8,496.9,5326,580.5,绘制 饼图并添加必要的图名和图示。 clc.clear.close all %生产量数据 explode =[1 000] %控制色调 colormap(summer) Pe3 rodc,.explode,)%参数explode表明将值等于1的饼切制出米显示 tle某工厂2016年度各季度生产值(单位:万元)) legend(第一季度,第二季度,第三季度,第四季度
X=C1*sin(A1*T); Y=C2*sin(A2*T+B(i)); subplot(2,3,i); plot(X,Y); end for i=1:5 X=C1*sin(A1*T); Y=C2*sin(A2*T+B(i)); subplot(2,3,6); plot(X,Y); hold on; end --------------------------------------------------------- 3. 某工厂2016年度各季度生产值(单位:万元)分别为547.8,496.9,532.6,580.5,绘制 饼图并添加必要的图名和图示。 clc,clear,close all %生产量数据 produce=[547.8 496.9 532.6 580.5]; %值为1可以突出显示 explode = [1 0 0 0]; %控制色调 colormap(summer); pie3(produce,explode); % 参数explode表明将值等于1的饼切割出来显示 %标题和图例 title('某工厂2016年度各季度生产值(单位:万元)') legend('第一季度','第二季度','第三季度','第四季度'); ---------------------------------------------------

某工厂2016年度各季度生产值(单位:万元) 27% 259 23% 4.设计求100个10000以内的随机数a1,a…0100由小到大的求和算法。 y=rand(1,100)*10000. yy=sort(y)片 s=sum(vy): 527994.466938443 5.在Fibonacci数列中,能够用MATLAB的浮点数精确表示而不出现上溢的最大的数是第 几项?能够用MATLAB的浮点数近似表示而不出现上澄的最大的数是第几项?编程验 证你的答案。 function [f.n)-fibomax %找出能在MATLAB中近似表示的最大项 f1)F1l:f21,n-2 while f(n)-inf n=n+l: f()=f(n-1)+f(n-2>. end nn-l f=f(n). >>[f,n]=fibomax f- 1.306989223763399e+308 n= 1476 %最大能用浮点数近似表示而不出现上溢的项 >>realmax(double') ans=
4. 设计求 100 个 10000 以内的随机数 a1,a2,…,a100 由小到大的求和算法。 y=rand(1,100)*10000; yy=sort(y); s=sum(yy); --------------------------------------------------- s= 527994.466938443 5. 在 Fibonacci 数列中,能够用 MATLAB 的浮点数精确表示而不出现上溢的最大的数是第 几项?能够用 MATLAB 的浮点数近似表示而不出现上溢的最大的数是第几项?编程验 证你的答案。 function [f,n]=fibomax % 找出能在MATLAB中近似表示的最大项 f(1)=1;f(2)=1;n=2; while f(n)~=inf n=n+1; f(n)=f(n-1)+f(n-2); end n=n-1; f=f(n); >> [f,n]=fibomax f = 1.306989223763399e+308 n = 1476 %最大能用浮点数近似表示而不出现上溢的项 >> realmax('double') ans =

1.797693134862316e+308 能用浮点数近似表示而不出现上溢的项是第1476项。 functiony,n)-fib(n)%检验是否精确表达的函数 %Generates fibonaccinumbers for the program fibonacci fz(11:fz(2)1: fork=3:n fz(k)-fz(k-l)+fz(k-2). end y-fz(n} ≥>,nib(79 y= 1.447233402467622e+16 n= 79 但实际上,第79项的精确值是1.4472334023676221e+16 这是由于MATLAB中双精度浮点数的最大精度表示范围是小数点后15位。所以 只能精确表达到第78项。 也可根据通项公式直接用flintmax和realmax?常数来求得最大的精确表示和近似 表示 通项公式如下: =-≥ 1 Fn代入flintmax从中解得n=78是最大的精确表达项;代入realmax从中解得n=1476 是最大的近似表达项。 >c=1/sart(5: >>phi=(sqrt(5)+1)/2; >>n=(log(flintmax)-log(c)log(phi) n= 78.014540730050044 >>m=(log(realmax)-log(c))/log(phi) m= 1.476662448520642e+03
1.797693134862316e+308 能用浮点数近似表示而不出现上溢的项是第 1476 项。 ------------------------------------------------------------------------------- function [y,n]=fib(n) %检验是否精确表达的函数 %Generates fibonacci numbers for the program fibonacci fz(1)=1;fz(2)=1; for k=3:n fz(k)=fz(k-1)+fz(k-2); end y=fz(n); >>[y,n]=fib(79) y = 1.447233402467622e+16 n = 79 但实际上,第79项的精确值是1.4472334023676221e+16 这是由于MATLAB中双精度浮点数的最大精度表示范围是小数点后15位。所以 只能精确表达到第78项。 也可根据通项公式直接用flintmax和realmax常数来求得最大的精确表示和近似 表示。 通项公式如下: 𝐹𝑛 = 1 √5 × (( 1 + √5 2 ) 𝑛 − ( 1 − √5 2 ) 𝑛 ) Fn代入flintmax从中解得n=78是最大的精确表达项;代入realmax从中解得n=1476 是最大的近似表达项。 >> c=1/sqrt(5); >> phi=(sqrt(5)+1)/2; >> n=(log(flintmax)-log(c))/log(phi) n = 78.014540730050044 >> m=(log(realmax)-log(c))/log(phi) m = 1.476662448520642e+03