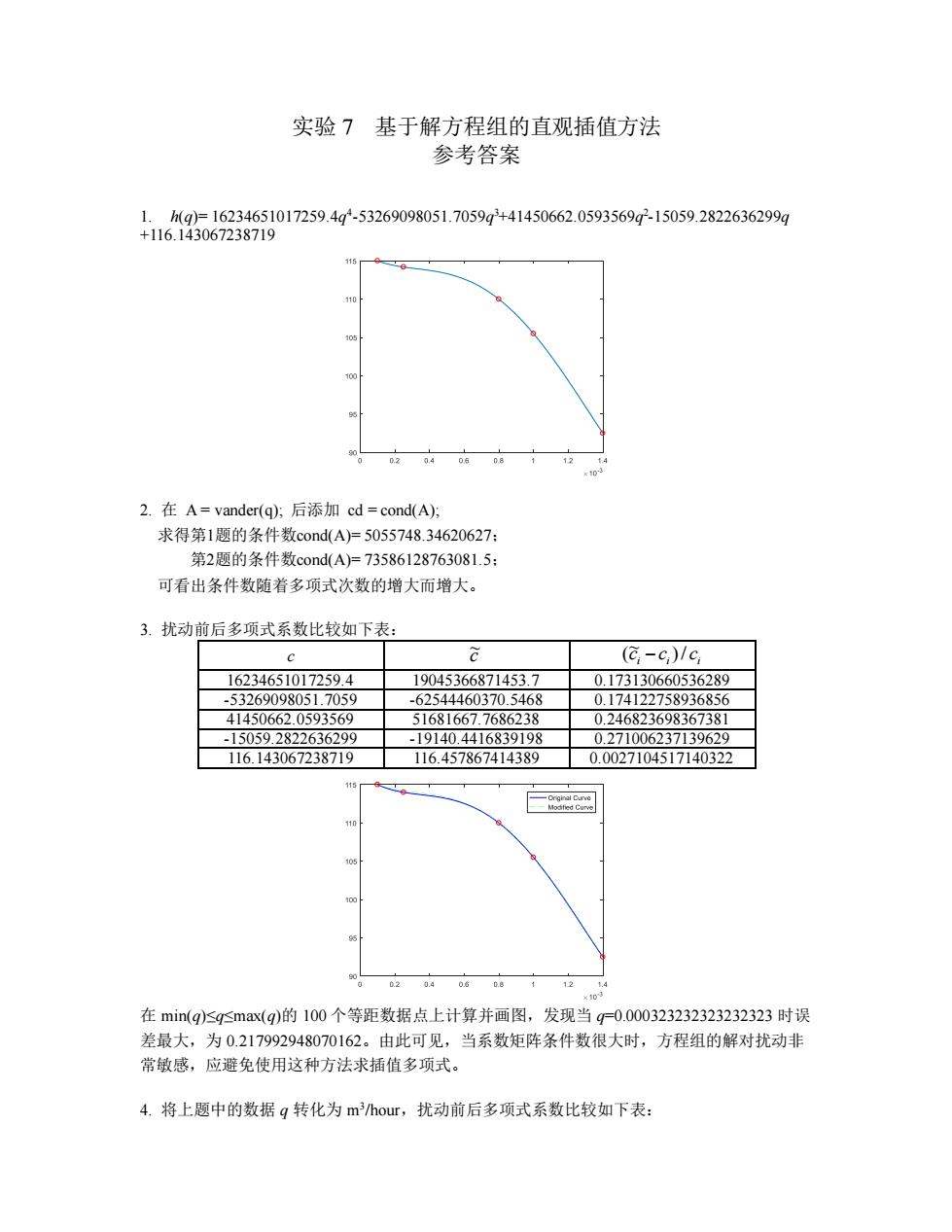
实验7基于解方程组的直观插值方法 参考答案 h685636ig0172594-532690905170591450620593569150592263629 2.在A=vander(q:后添加cd=cond(A: 求得第1题的条件数cond(A)=5055748.34620627: 第2题的条件数cond(A)=73586128763081.5: 可看出条件数随者多项式次数的增大而增大。 3.扰动前后多项式系数比较如下表: (C,-c)c 16234651017259.4 19045366871453.7 -53269098051.7059 -62544460370.5468 419 116.143067238719 116.457867414389 0.0027104517140322 在min(q)s9gmax(g)的100个等距数据点上计算并画图,发现当g-0.000323232323232323时误 差最大,为0.217992948070162。由此可见,当系数矩阵条件数很大时,方程组的解对扰动非 常敏感,应避免使用这种方法求插值多项式 4.将上题中的数据q转化为m/hour,扰动前后多项式系数比较如下表:
实验 7 基于解方程组的直观插值方法 参考答案 1. h(q)= 16234651017259.4q 4 -53269098051.7059q 3+41450662.0593569q 2 -15059.2822636299q +116.143067238719 2. 在 A = vander(q); 后添加 cd = cond(A); 求得第1题的条件数cond(A)= 5055748.34620627; 第2题的条件数cond(A)= 73586128763081.5; 可看出条件数随着多项式次数的增大而增大。 3. 扰动前后多项式系数比较如下表: c c ~ i i i c c )/ c ~( − 16234651017259.4 19045366871453.7 0.173130660536289 -53269098051.7059 -62544460370.5468 0.174122758936856 41450662.0593569 51681667.7686238 0.246823698367381 -15059.2822636299 -19140.4416839198 0.271006237139629 116.143067238719 116.457867414389 0.0027104517140322 在 min(q)≤q≤max(q)的 100 个等距数据点上计算并画图,发现当 q=0.000323232323232323 时误 差最大,为 0.217992948070162。由此可见,当系数矩阵条件数很大时,方程组的解对扰动非 常敏感,应避免使用这种方法求插值多项式。 4. 将上题中的数据 q 转化为 m3 /hour,扰动前后多项式系数比较如下表:
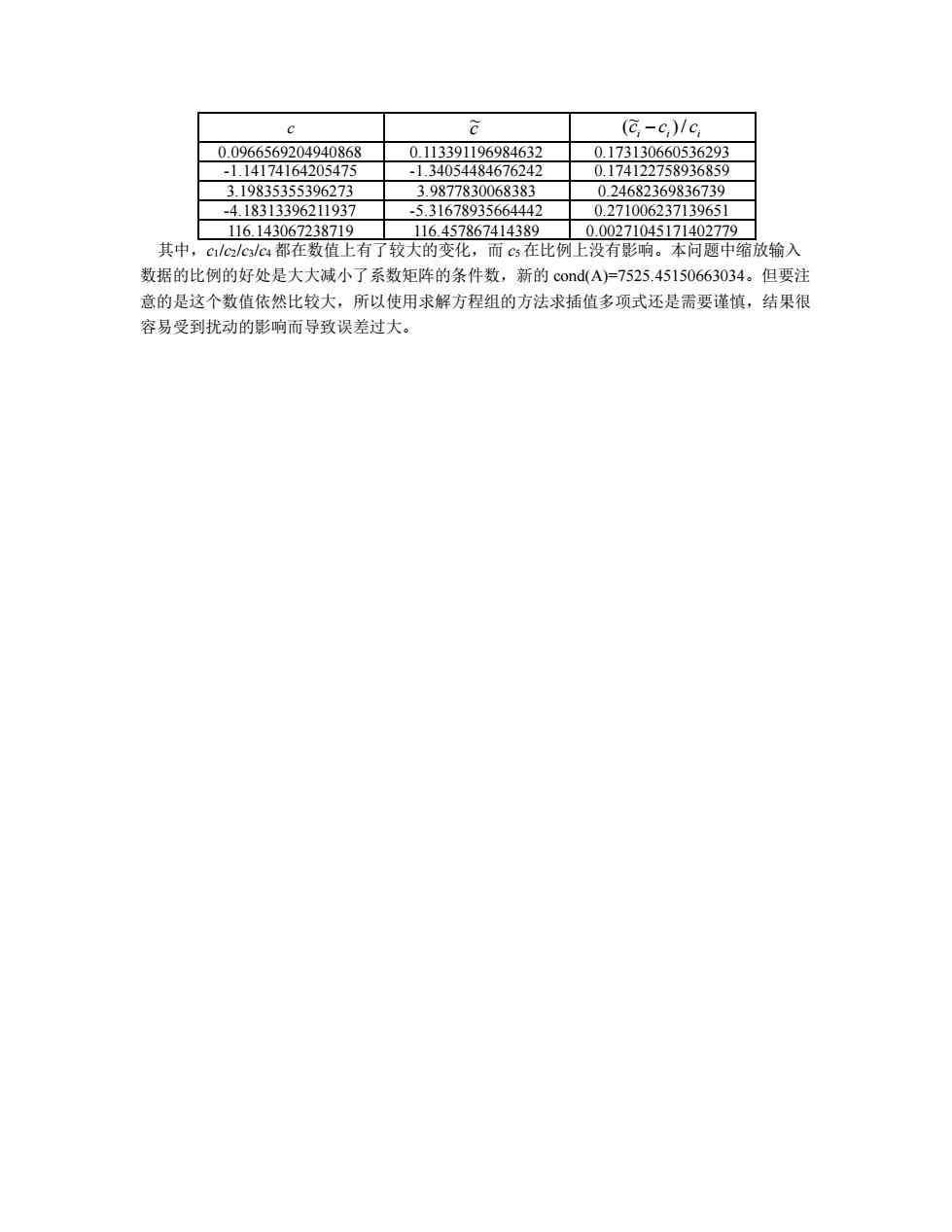
(,-c)/c 0.09 20494 69846 5060 562 987783006838 2603092730 418313396211037 53167803566444) 0271006237130651 116.143067238719 116.457867414389 0.00271045171402779 其中,cc/c/c:都在数值上有了较大的变化,而cs在比例上没有影响。本问题中缩放输入 数据的比例的好处是大大减小了系数矩阵的条件数,新的cod(A)-7525.45150663034。但要注 意的是这个数值依然比较大,所以使用求解方程组的方法求插值多项式还是需要谨慎,结果很 容易受到扰动的影响而导致误差过大
c c ~ i i i c c )/ c ~( − 0.0966569204940868 0.113391196984632 0.173130660536293 -1.14174164205475 -1.34054484676242 0.174122758936859 3.19835355396273 3.9877830068383 0.24682369836739 -4.18313396211937 -5.31678935664442 0.271006237139651 116.143067238719 116.457867414389 0.00271045171402779 其中,c1/c2/c3/c4 都在数值上有了较大的变化,而 c5 在比例上没有影响。本问题中缩放输入 数据的比例的好处是大大减小了系数矩阵的条件数,新的 cond(A)=7525.45150663034。但要注 意的是这个数值依然比较大,所以使用求解方程组的方法求插值多项式还是需要谨慎,结果很 容易受到扰动的影响而导致误差过大