实验9分段多项式插值 参考答案 1.由于有10个数据点,所以要使用9次多项式进行插值。考虑到拉格朗日 方法形成的插值多项式舍入误差比较小,所以使用拉格朗日插值方法,得到 Lx=-0.000665509259259259x+0.0329365079365079xr. 06 6800595238 5x+8.23069444444445.59.4823784722222r+270.938194444444r 71.732060185185x+131259817460317.194.3880952381r+438 易见,插值曲线出现了多处多余的振荡,这是由于插值曲线的次数过高 引起的。 2.由于数据点明显分成两部分,利用分段线性函数手工完成插值,得到 -0.5x+4x∈[1,5 P(x)={-3.9x+25.5x∈[5,6 -0.4x+12.4x∈[6,10] 可见,虽然消除了振荡,但是分段线性多项式曲线不光滑。 3.分段三次Hermite插值需要在每个数据点上给出该点的斜率,在x=5和x=6 两个点上,取左右导数的算术平均值作为该点的斜率,其余各点根据给定数 据计算得到对应斜率。 分段三次Hermite插值多项式函数:function yhat=hermint(x,ffp,xhat)(见代 码文件》 运行程序计算得到的分段三次Hermite插值多项式为
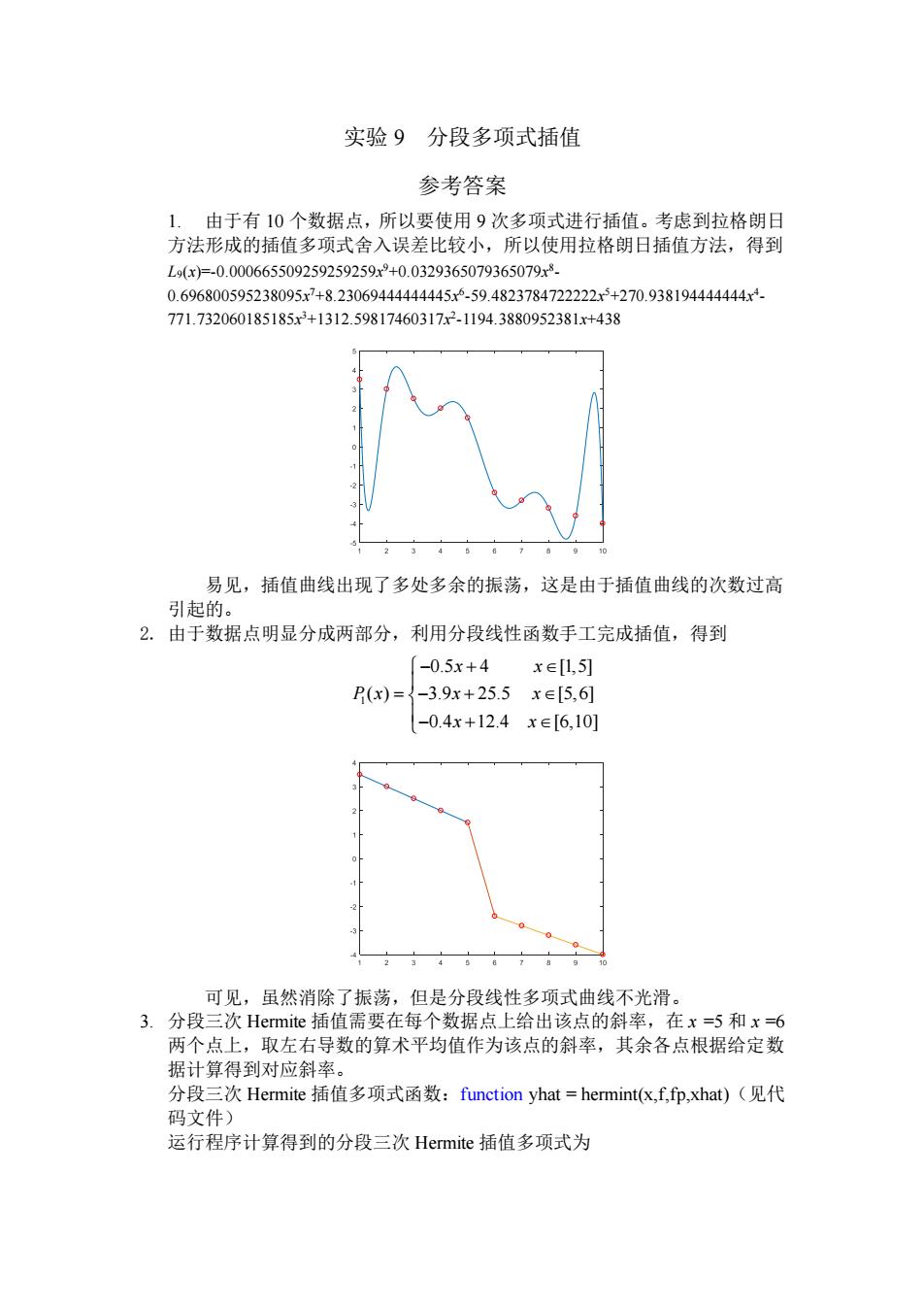
实验 9 分段多项式插值 参考答案 1. 由于有 10 个数据点,所以要使用 9 次多项式进行插值。考虑到拉格朗日 方法形成的插值多项式舍入误差比较小,所以使用拉格朗日插值方法,得到 L9(x)=-0.000665509259259259x 9+0.0329365079365079x 8 - 0.696800595238095x 7+8.23069444444445x 6 -59.4823784722222x 5+270.938194444444x 4 - 771.732060185185x 3+1312.59817460317x 2 -1194.3880952381x+438 易见,插值曲线出现了多处多余的振荡,这是由于插值曲线的次数过高 引起的。 2. 由于数据点明显分成两部分,利用分段线性函数手工完成插值,得到 1 0.5 4 [1,5] ( ) 3.9 25.5 [5,6] 0.4 12.4 [6,10] x x P x x x x x − + = − + − + 可见,虽然消除了振荡,但是分段线性多项式曲线不光滑。 3. 分段三次 Hermite 插值需要在每个数据点上给出该点的斜率,在 x =5 和 x =6 两个点上,取左右导数的算术平均值作为该点的斜率,其余各点根据给定数 据计算得到对应斜率。 分段三次 Hermite 插值多项式函数:function yhat = hermint(x,f,fp,xhat)(见代 码文件) 运行程序计算得到的分段三次 Hermite 插值多项式为
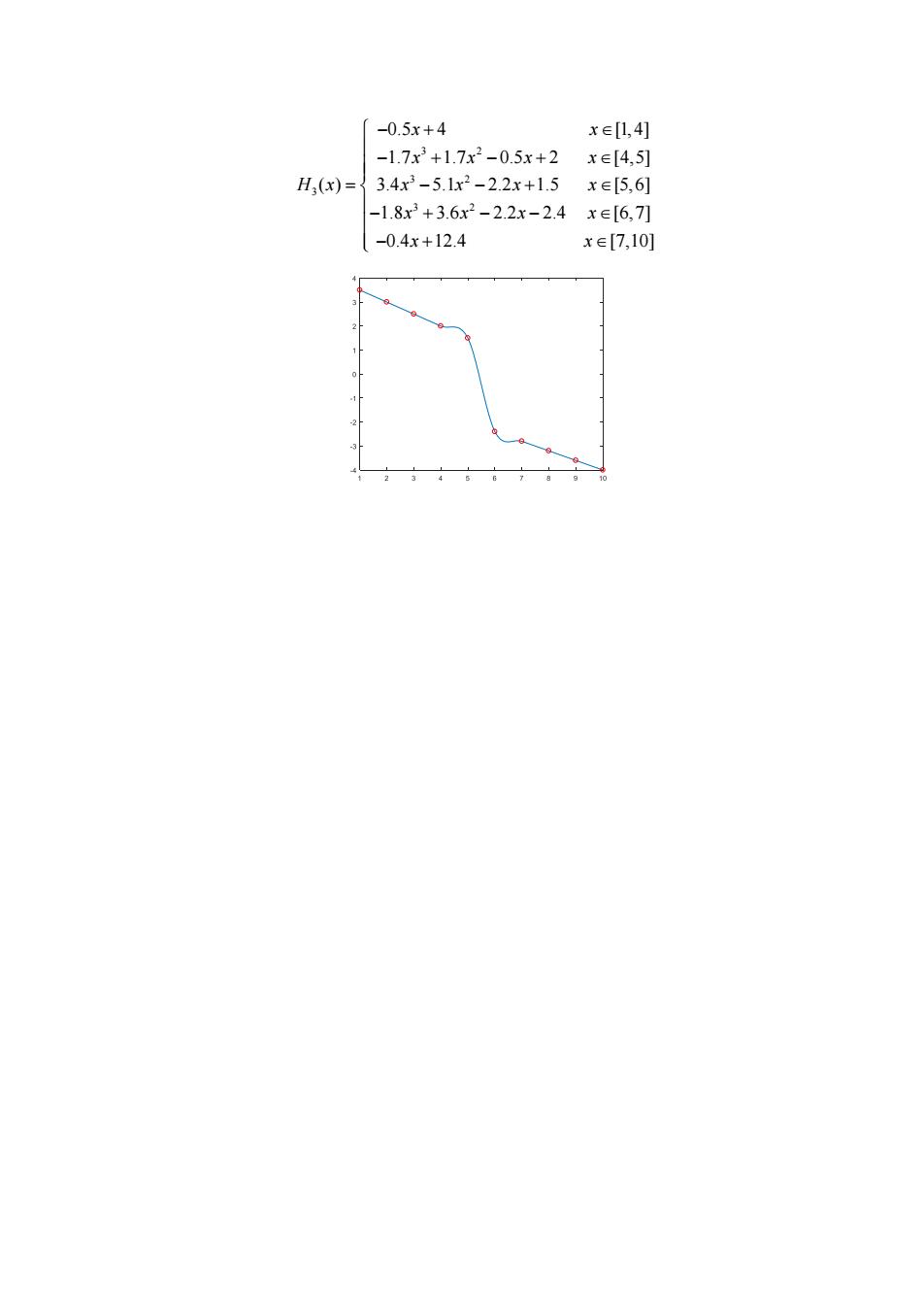
-0.5x+4 x∈l,4 -1.7x2+1.7x2-0.5x+2 xe[4,5] H(x)= 3.4x2-5.1x2-2.2x+1.5 x∈5,6 -1.8x2+3.6x2-2.2x-2.4xe[6.7刀 -0.4x+12.4 xe7,10
3 2 3 2 3 3 2 0.5 4 [1,4] 1.7 1.7 0.5 2 [4,5] ( ) 3.4 5.1 2.2 1.5 [5,6] 1.8 3.6 2.2 2.4 [6,7] 0.4 12.4 [7,10] x x x x x x H x x x x x x x x x x x − + − + − + = − − + − + − − − +