
实验14数值最优化方法 参考答案 1.首先画出函数图形如下,可见该函数在给定区间1,5]上是单峰函数,适合使用精确 线搜索算法求最小值。 1322335 黄金分割搜索法:function [S,E,G)-golden(,f.a,b,delta,epsilon)(见代码文件) Fibonaccif搜索法:function [X.E..G-fibonacci(f.a.b.toLe)(见代码文件) 其中,需要调用生成Fibonacci序列的程序:functiony,nib()(见代码文件) 抛物线搜索法:function [p,.yp,dp,dy.P=quadmin(Cab,dela,epsilon))(见代码文件) 取横坐标容许误差10~9,纵坐标容许误差10-1l,Fibonacci搜素法中的区别常数为0.001,三 种算法的求解结果比较如下表: 算法黄金分制搜索法Fibonacci搜索法抛物线搜索法 最小值点 6.3333572737 (6.333333435288 (3.3333333358177 4.48148148148148 4.48148148148147 4.48148148148147 3.720947994168e10. 误差 (1.73874248332595e-11, (3.47860563603882e-09. 01 0) 7.105427357601c-15) 迭代次数 46 6 收敛阶 线性 线性 超线性 3.(1)画图程序见代码文件FigBanana.m,函数图形和等高线图如图1-图3所示: 05 图1函数图 图2等高线图
实验 14 数值最优化方法 参考答案 1. 首先画出函数图形如下,可见该函数在给定区间[1,5]上是单峰函数,适合使用精确 线搜索算法求最小值。 黄金分割搜索法:function [S,E,G]=golden(f,a,b,delta,epsilon)(见代码文件) Fibonacci搜索法:function [X,E,G]=fibonacci(f,a,b,tol,e) (见代码文件) 其中,需要调用生成Fibonacci序列的程序:function [y,n]=fib(n) (见代码文件) 2. 抛物线搜索法:function [p,yp,dp,dy,P] = quadmin(f,a,b,delta,epsilon) (见代码文件) 取横坐标容许误差 10-9,纵坐标容许误差 10-11,Fibonacci 搜索法中的区别常数为 0.001,三 种算法的求解结果比较如下表: 算法 黄金分割搜索法 Fibonacci 搜索法 抛物线搜索法 最小值点 (3.33333335727376, 4.48148148148148) (3.33333333435288, 4.48148148148147) (3.3333333358177, 4.48148148148147) 误差 (3.720947994168e-10, 0) (1.73874248332595e-11, 0) (3.47860563603882e-09, 7.105427357601e-15) 迭代次数 41 46 6 收敛阶 线性 线性 超线性 3. (1)画图程序见代码文件 FigBanana.m,函数图形和等高线图如图 1-图 3 所示: 图 1 函数图 图 2 等高线图
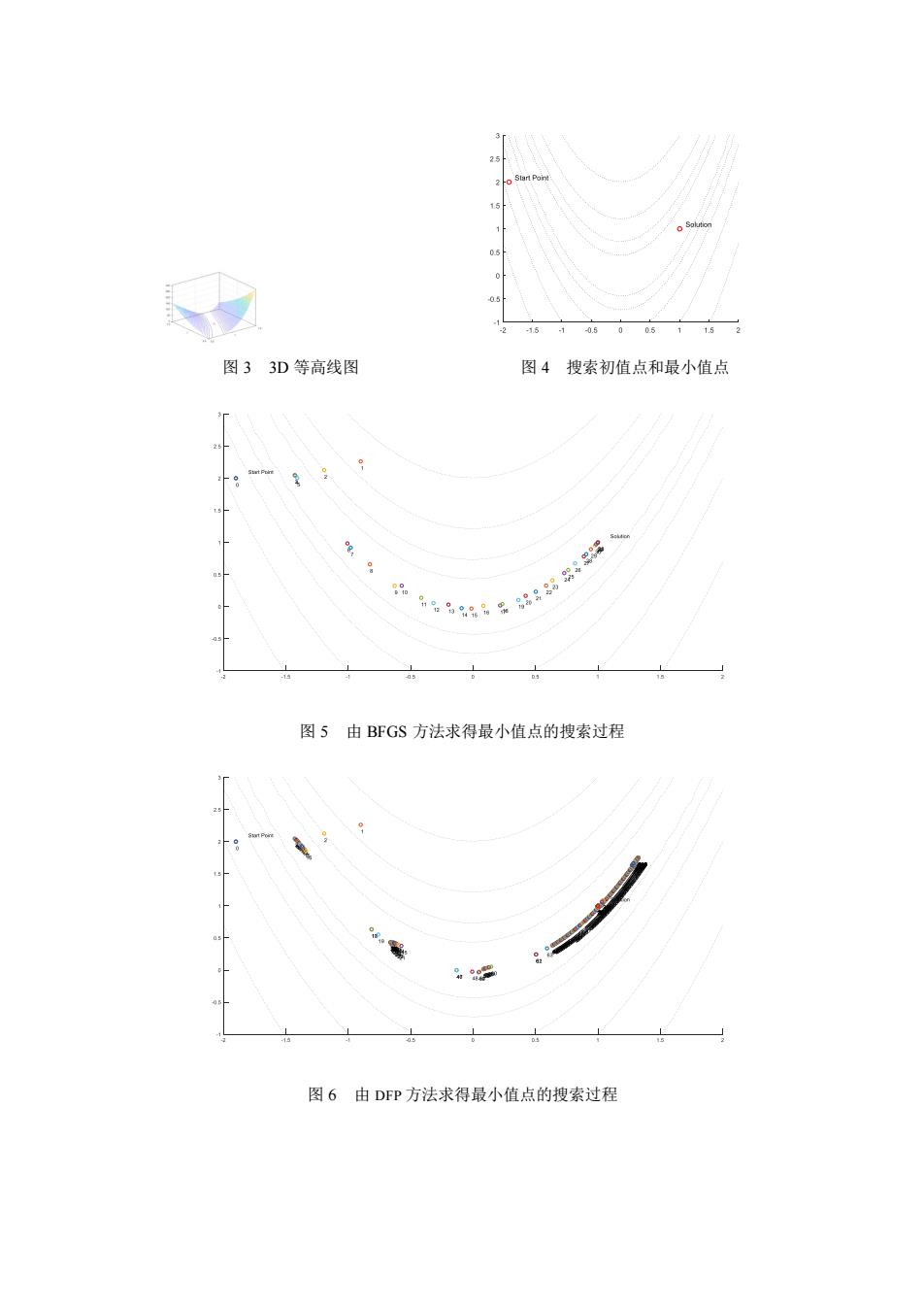
-1510505 15 图33D等高线图 图4搜索初值点和最小值点 图5由BFGS方法求得最小值点的搜索过程 图6由DFP方法求得最小值点的搜索过程
图 3 3D 等高线图 图 4 搜索初值点和最小值点 图 5 由 BFGS 方法求得最小值点的搜索过程 图 6 由 DFP 方法求得最小值点的搜索过程
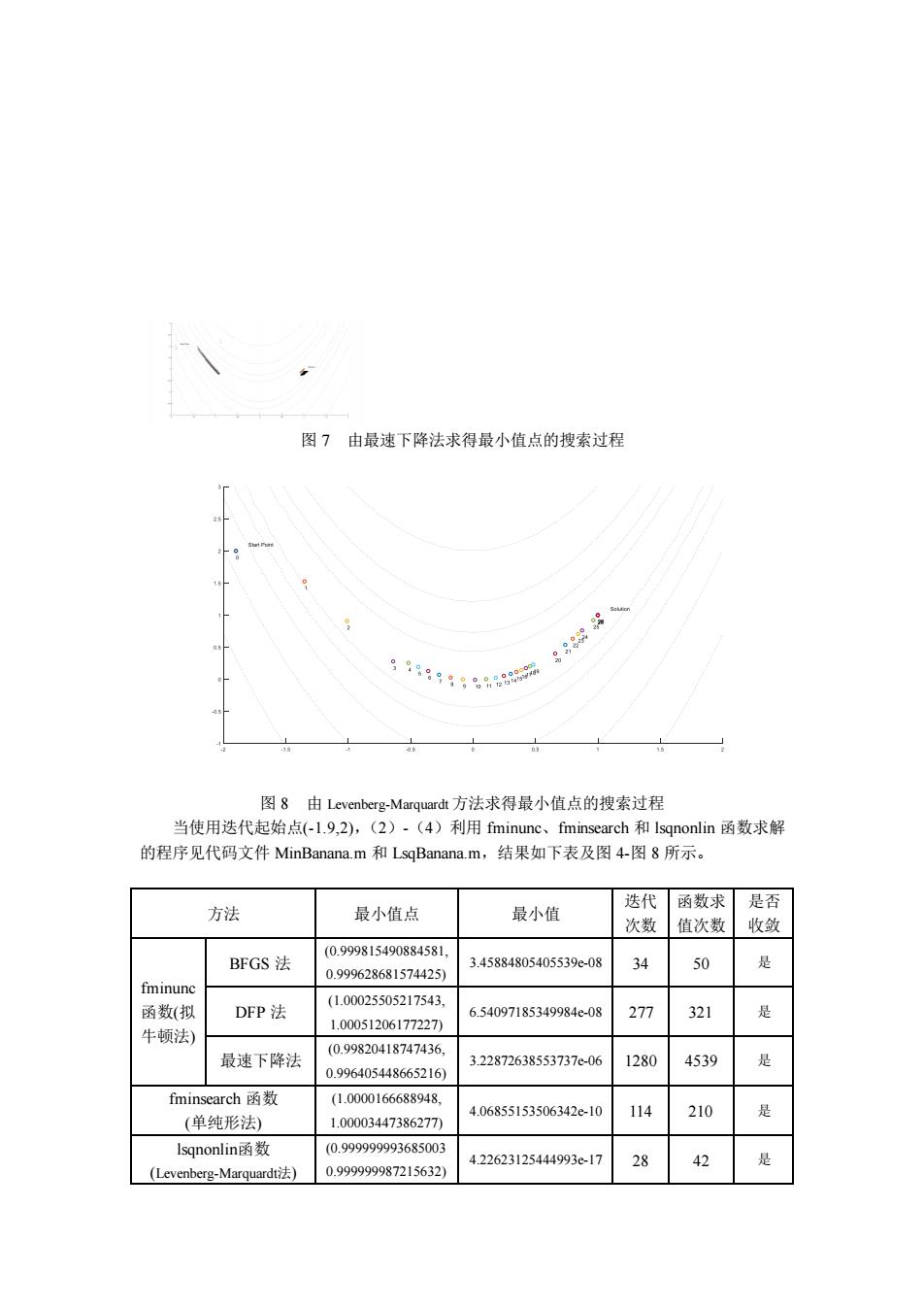
图7由最速下降法求得最小值点的搜索过程 988883a 图8由Levenber-Marquard.方法求得最小值点的博索讨程 当使用迭代起始点1.9,2,(2).(4)利用m aunc、fminsearch和Isqnonlin函数求解 的程序见代码文件MinBanana.m和LsqBanana.m,结果如下表及图4-图8所示。 方法 最小值点 最小值 迭代函数求是否 次数 值次数收敛 BFGS法 0981549084658 0.999628681574425) 3.45884805405539e-08 34 50 是 fminunc 函新(拟 DFP法 (1.00025505217543. 6.54097185349984e-08 277 321 1.00051206177227分 牛顿法) 最速下降法 (0.99820418747436. 0.99640544865216 322872638553737c-06 1280 4539 是 fminsearch函数 (1.0000166688948 4.06855153506342c-10 (单纯形法) 114 210 1.00003447386277) 0999999993685003 998721632 4.22623125444993e-17 28 42 是 (Levenberg-Marquardi)
图 7 由最速下降法求得最小值点的搜索过程 图 8 由 Levenberg-Marquardt 方法求得最小值点的搜索过程 当使用迭代起始点(-1.9,2),(2)-(4)利用 fminunc、fminsearch 和 lsqnonlin 函数求解 的程序见代码文件 MinBanana.m 和 LsqBanana.m,结果如下表及图 4-图 8 所示。 方法 最小值点 最小值 迭代 次数 函数求 值次数 是否 收敛 fminunc 函数(拟 牛顿法) BFGS 法 (0.999815490884581, 0.999628681574425) 3.45884805405539e-08 34 50 是 DFP 法 (1.00025505217543, 1.00051206177227) 6.54097185349984e-08 277 321 是 最速下降法 (0.99820418747436, 0.996405448665216) 3.22872638553737e-06 1280 4539 是 fminsearch 函数 (单纯形法) (1.0000166688948, 1.00003447386277) 4.06855153506342e-10 114 210 是 lsqnonlin函数 (Levenberg-Marquardt法) (0.999999993685003 0.999999987215632) 4.22623125444993e-17 28 42 是

Resenbrock函数为两个平方数的和,当x=x=时,整个目标函数有最小值0。可以看 出, 在相同的设置下,最速下降法得到的结果最差。这是因为最速下降法特别不适合于从 狭长通道到达最优解的情况。另一方面,使用默认的BFGS方法的fminunc函数的效率明显 高于fminsearch函数,因为对目标函数调用的次数与迭代的步数都明显少于后者,但由前者 得出的解的精度没有后者高。而在这个求平方和最小的具体问题中,使用Isqnonlin函数把 问题当作最小二乘优化问题来求解显然比上述两种方法更合适。 从三维等高线图 (图3)中可以看出,函数的最小值点在图中的一个很窄的白色带状区 域内,在这个区域内函数值的变化较为平缓,形如香蕉,故Rosenbrock函数又称为香蕉函 数。这种在最值点附近变化缓慢的特性会造成算法在解点附近选代过慢的问题。所以这个函 数经常用来测试最优化算法的优劣
Resenbrock 函数为两个平方数的和,当 x1=x2=1 时,整个目标函数有最小值 0。可以看 出,在相同的设置下,最速下降法得到的结果最差。这是因为最速下降法特别不适合于从一 狭长通道到达最优解的情况。另一方面,使用默认的 BFGS 方法的 fminunc 函数的效率明显 高于 fminsearch 函数,因为对目标函数调用的次数与迭代的步数都明显少于后者,但由前者 得出的解的精度没有后者高。而在这个求平方和最小的具体问题中,使用 lsqnonlin 函数把 问题当作最小二乘优化问题来求解显然比上述两种方法更合适。 从三维等高线图(图 3)中可以看出,函数的最小值点在图中的一个很窄的白色带状区 域内,在这个区域内函数值的变化较为平缓,形如香蕉,故 Rosenbrock 函数又称为香蕉函 数。这种在最值点附近变化缓慢的特性会造成算法在解点附近迭代过慢的问题。所以这个函 数经常用来测试最优化算法的优劣