实验13数值微分和数值积分 参考答案 1.编写变步长求导数近似值程序:function L=diffexp((f,x)(见代码文件) 计算结果如下: h 0.40 ERR RE 2.75319416537532 0 0.12.49431231562062 0.2588818497546990.0986685202551917 001249184956151056000246275411006280000987835602112365 0.0012.491824946278752.46152318084114e-059.87834649712321e-0 0.00012.49182470012821 2.4615054439181e-079.87832459568164e-08 1e-052491824697659072.46913600676635e-099.90894747877984e-10 1c-06249182469769238333062466495448e.11133662077756158e-11 2.49182469769238 1e-082.491824702133274.44089209850063e-091.78218479761276c-09 1e-092.491824857564491.55431223003433e-076.23764657372333c-08 从上表可以看出,随着步长的减小,误差逐步减小,但是在某个时刻后误差 又逐步增大,这说明存在一个最佳步长。实际上,这里的误差包含了两部分: 方法误差和舍入误差。方法误差随着步长的减小逐步减小,而舍入误差则随 着步长的减小反而逐步增加。 2.编写三点公式求给定节点上的数值导数程序:function dy=difftripts(xy)(见 代码文件) 计算结果如下: ‘T 5 0.1 0.2 0.3 0.4 0.5 0.6 /x)120s1091sx65 1.4214他7107164985875%1.891824097641272.1487212W01324221180s9061 /2019m16 2223439475%2352106740552.494312315606226514053761921640080061段 3.编写样条公式求非节点的数值导数程序:function dy--diffspline(xy,dy,xO)(见 代码文件)计算结果如下: 精确值 近似值 °(0.25)2.284025416687742.28295345501067 f*(0.25)1.284025416687741.2867024990372 从上面结果比较看出,可用三次样条数值微分公式求非节点上的导数近似值。 具体做法就是结合上题的步骤,先利用第2题比较简单的三点微分公式(或
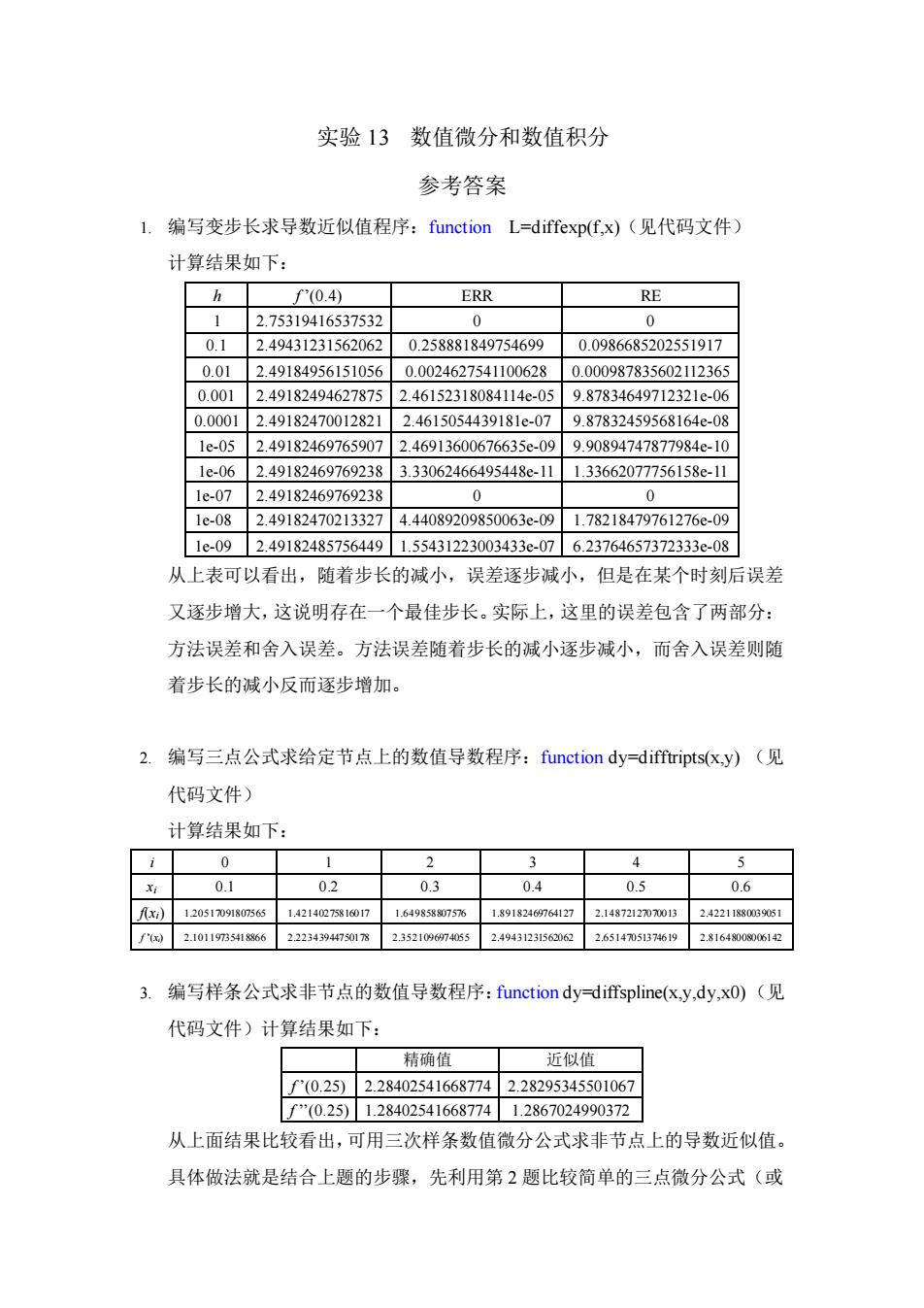
实验 13 数值微分和数值积分 参考答案 1. 编写变步长求导数近似值程序:function L=diffexp(f,x)(见代码文件) 计算结果如下: h f ’(0.4) ERR RE 1 2.75319416537532 0 0 0.1 2.49431231562062 0.258881849754699 0.0986685202551917 0.01 2.49184956151056 0.0024627541100628 0.000987835602112365 0.001 2.49182494627875 2.46152318084114e-05 9.87834649712321e-06 0.0001 2.49182470012821 2.4615054439181e-07 9.87832459568164e-08 1e-05 2.49182469765907 2.46913600676635e-09 9.90894747877984e-10 1e-06 2.49182469769238 3.33062466495448e-11 1.33662077756158e-11 1e-07 2.49182469769238 0 0 1e-08 2.49182470213327 4.44089209850063e-09 1.78218479761276e-09 1e-09 2.49182485756449 1.55431223003433e-07 6.23764657372333e-08 从上表可以看出,随着步长的减小,误差逐步减小,但是在某个时刻后误差 又逐步增大,这说明存在一个最佳步长。实际上,这里的误差包含了两部分: 方法误差和舍入误差。方法误差随着步长的减小逐步减小,而舍入误差则随 着步长的减小反而逐步增加。 2. 编写三点公式求给定节点上的数值导数程序:function dy=difftripts(x,y) (见 代码文件) 计算结果如下: i 0 1 2 3 4 5 xi 0.1 0.2 0.3 0.4 0.5 0.6 f(xi) 1.20517091807565 1.42140275816017 1.649858807576 1.89182469764127 2.14872127070013 2.42211880039051 f ’(xi) 2.10119735418866 2.22343944750178 2.3521096974055 2.49431231562062 2.65147051374619 2.81648008006142 3. 编写样条公式求非节点的数值导数程序:function dy=diffspline(x,y,dy,x0)(见 代码文件)计算结果如下: 精确值 近似值 f ’(0.25) 2.28402541668774 2.28295345501067 f ’’(0.25) 1.28402541668774 1.2867024990372 从上面结果比较看出,可用三次样条数值微分公式求非节点上的导数近似值。 具体做法就是结合上题的步骤,先利用第 2 题比较简单的三点微分公式(或

五点微分公式)求出等距节点上的一阶导数,然后再利用三次样条微分公式 求出非节点处的一阶甚至二阶数值导数(包括节点处的二阶导数)。这克服了 基于插值多项式的数值微分公式只能求解插值节点上的导数近似值的缺点, 而且还避免了求解三弯矩方程组或三转角方程组 4.复合梯形公式程序:function[t2,M=-contra(fa,b,tol(见代码文件) 复合Simpson公式程序:function[s2,M]-consim(fa,b,tol(见代码文件) 方法 近似值 子区间数 复合梯形公式 55.1696660852374 524288 L复合Simpson公式55.16966608507731024☐ 从上面结果比较看出,为了达到指定的数值精度,采用复合Simpson公式需 要的子区间数比复合梯形公式少得多,这意味着需要的函数求值少得多。这 是因为Simpson公式比梯形公式高阶,误差更小。所以我们常用复合Simpson 公式求积分的数值解 5.基于Simpson公式的自适应数值积分程序: function[SRmat,quad,er,tola=adapt(f,ab,tol(见代a码文件) 其中,需要调用利用Simpson公式计算单个区间上积分值的程序: functionZ=srule(f,a0,b0,tolO)(见代a码文件) 结果如下:quad=0.671757865393781 为达到1×109的精度,总共划分了101个子区间
五点微分公式)求出等距节点上的一阶导数,然后再利用三次样条微分公式 求出非节点处的一阶甚至二阶数值导数(包括节点处的二阶导数)。这克服了 基于插值多项式的数值微分公式只能求解插值节点上的导数近似值的缺点, 而且还避免了求解三弯矩方程组或三转角方程组。 4. 复合梯形公式程序:function [t2,M]=contra(f,a,b,tol)(见代码文件) 复合 Simpson 公式程序:function [s2,M]=consim(f,a,b,tol)(见代码文件) 方法 近似值 子区间数 复合梯形公式 55.1696660852374 524288 复合 Simpson 公式 55.1696660850773 1024 从上面结果比较看出,为了达到指定的数值精度,采用复合 Simpson 公式需 要的子区间数比复合梯形公式少得多,这意味着需要的函数求值少得多。这 是因为 Simpson 公式比梯形公式高阶,误差更小。所以我们常用复合 Simpson 公式求积分的数值解。 5. 基于 Simpson 公式的自适应数值积分程序: function [SRmat,quad,err,tola]=adapt(f,a,b,tol)(见代码文件) 其中,需要调用利用 Simpson 公式计算单个区间上积分值的程序: function Z=srule(f,a0,b0,tol0) (见代码文件) 结果如下:quad = 0.671757865393781 为达到 1×10-9 的精度,总共划分了 101 个子区间

6.Romberg积分程序:function[R,quad,er,h]=romber(f,a,b,n,tol)(见代码文件) Gauss-Legendre方法程序:function quad=gaussleg(f,a,b,n)(见代码文件》 其中,需要调用自动计算n阶公式的节点位置及权系数的Schwarz算法程序: function[A,W=Schwarz(n)(见代码文件) 结果如下:精确值ln(3=1.09861228866811 方法 近似值 误差 Simpson公式 1.11111111111111 -0.0124988224430016 Boole公式 1.09925925925926 -0.000646970591149598 Romberg方法 1.09861228866811 2.07500683302442e12 3点G-L公式 1.09803921568627 0.000573072981835399 5点G-L公式 1.09860924181247 3.0468556373453e-06 组合3点G-L方法1.09858617399601 2.61146720998973e-05 其中,Romberg方法提阶7次,直至误差小于1×10,这时候区间划分个数 为128 从上面结果比较可以得出如下结论: (1)不管是哪类公式,节点数目越多,精度越高: (2)相同节点数目的Gauss-Legendre公式比闭型Newton--Cotes公式精度 高: (3)不管是哪种方法,细分区间都能使数值积分精度提高。区间划分越细, 精度越高
6. Romberg 积分程序:function [R,quad,err,h]=romber(f,a,b,n,tol)(见代码文件) Gauss-Legendre 方法程序:function quad=gaussleg(f,a,b,n)(见代码文件) 其中,需要调用自动计算 n 阶公式的节点位置及权系数的 Schwarz 算法程序: function [A,W]=Schwarz(n)(见代码文件) 结果如下:精确值 ln(3)=1.09861228866811… 方法 近似值 误差 Simpson 公式 1.11111111111111 -0.0124988224430016 Boole 公式 1.09925925925926 -0.000646970591149598 Romberg 方法 1.09861228866811 2.07500683302442e-12 3 点 G-L 公式 1.09803921568627 0.000573072981835399 5 点 G-L 公式 1.09860924181247 3.0468556373453e-06 组合 3 点 G-L 方法 1.09858617399601 2.61146720998973e-05 其中,Romberg 方法提阶 7 次,直至误差小于 1×10-9,这时候区间划分个数 为 128 从上面结果比较可以得出如下结论: (1) 不管是哪类公式,节点数目越多,精度越高; (2) 相同节点数目的 Gauss-Legendre 公式比闭型 Newton-Cotes 公式精度 高; (3) 不管是哪种方法,细分区间都能使数值积分精度提高。区间划分越细, 精度越高