
实验10样条插值 参考答案 1.各边界条件的插值样条生成函数见代码文件: (1)自然边界样条:functionS=-cnsfit(X,Y) (2)端点曲率调整样条:function S=cepcasfit(X,Y,dx20,dx2n) (3)紧压样条:functionS=csfit(X,Y,dx0,dxn) (4)外推样条:function S=cesfit((X,Y) (5)抛物线终结样条:functionS=cptsfit(X,Y) 利用上述各函数计算及绘图,得到如下结果: (1)自然边界样条计算及绘图代码段,输出如图1。 x05 y=x.*exp(-x). nS-=cnsfit(x,.y) x1=0:.01:1:y1=polyval(nS(I.).x1-x(1)): x2=1:.01:2y2=polyval(nS(2,),x2-x2 x3=2:.01:3y3=polyval(nS(3,),x3-x(3) x4=3:.01:4y4=polyval(nS(4,),x4-x(4) x5-4:.01:5:y5-polyval(nS(5.).x5-x(5)). figure,plot(x1,y1,x2.y2,x3.y3.x4.y4,x5.y5,x.y,'ro),title('natural spline) (2)端点曲率调整样条代码段(与(1)类似),输出如图2。 (3)紧压样条代码段(与(1)类似),输出如图3。 (4)外推样条代码段(与(1)类似),输出如图4。 (5)抛物线终结样条代码段(与(1)类似),输出如图5
实验 10 样条插值 参考答案 1. 各边界条件的插值样条生成函数见代码文件: (1)自然边界样条:function S=cnsfit(X,Y) (2)端点曲率调整样条:function S=cepcasfit(X,Y,dx20,dx2n) (3)紧压样条:function S=csfit(X,Y,dx0,dxn) (4)外推样条:function S=cesfit(X,Y) (5)抛物线终结样条:function S=cptsfit(X,Y) 利用上述各函数计算及绘图,得到如下结果: (1) 自然边界样条计算及绘图代码段,输出如图 1。 x=0:5; y=x.*exp(-x); nS=cnsfit(x,y); x1=0:.01:1;y1=polyval(nS(1,:),x1-x(1)); x2=1:.01:2;y2=polyval(nS(2,:),x2-x(2)); x3=2:.01:3;y3=polyval(nS(3,:),x3-x(3)); x4=3:.01:4;y4=polyval(nS(4,:),x4-x(4)); x5=4:.01:5;y5=polyval(nS(5,:),x5-x(5)); figure,plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x,y,'ro'),title('natural spline') (2) 端点曲率调整样条代码段(与(1)类似),输出如图 2。 (3) 紧压样条代码段(与(1)类似),输出如图 3。 (4) 外推样条代码段(与(1)类似),输出如图 4。 (5) 抛物线终结样条代码段(与(1)类似),输出如图 5
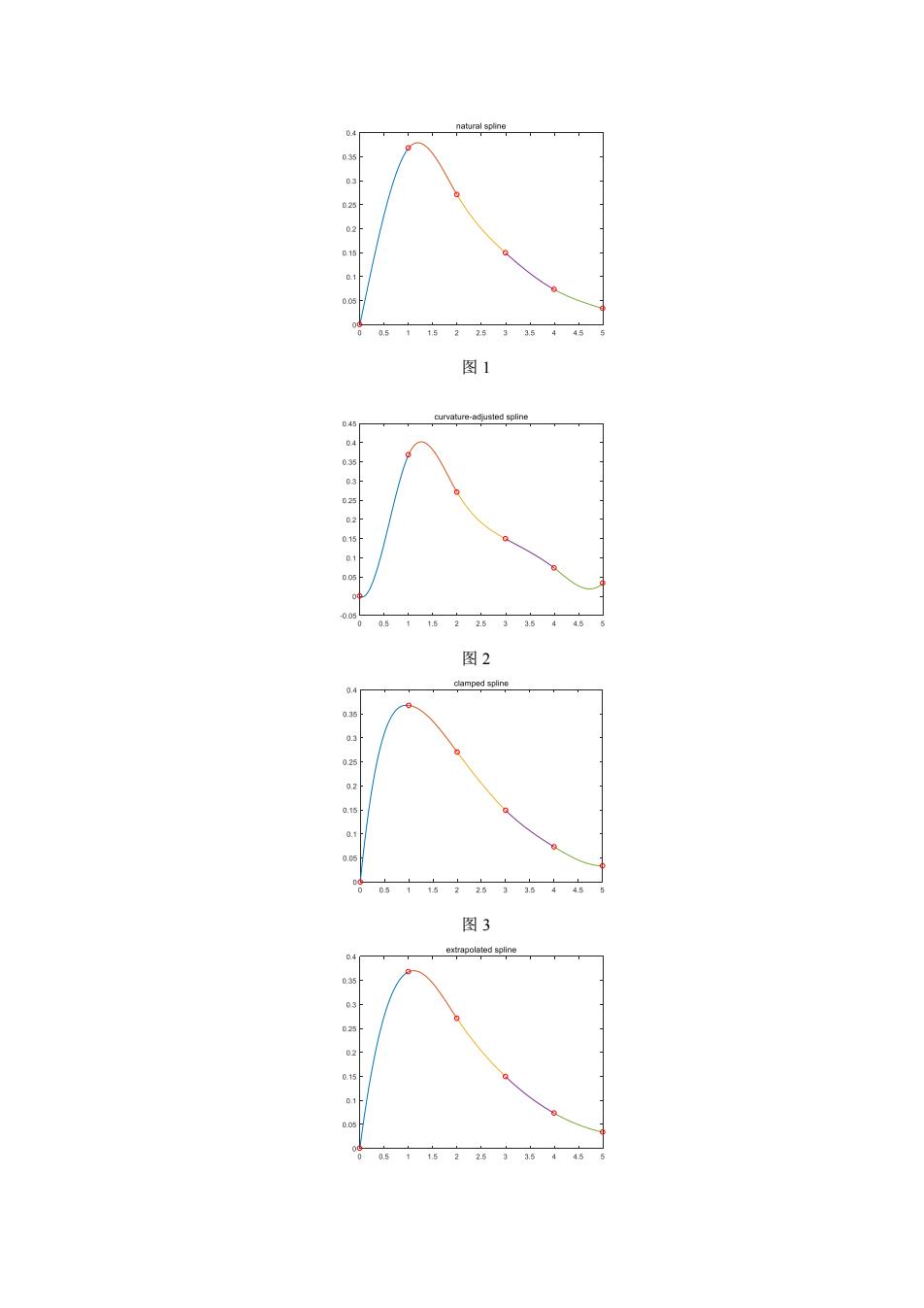
图1 图2 1 图3 02
图 1 图 2 图 3
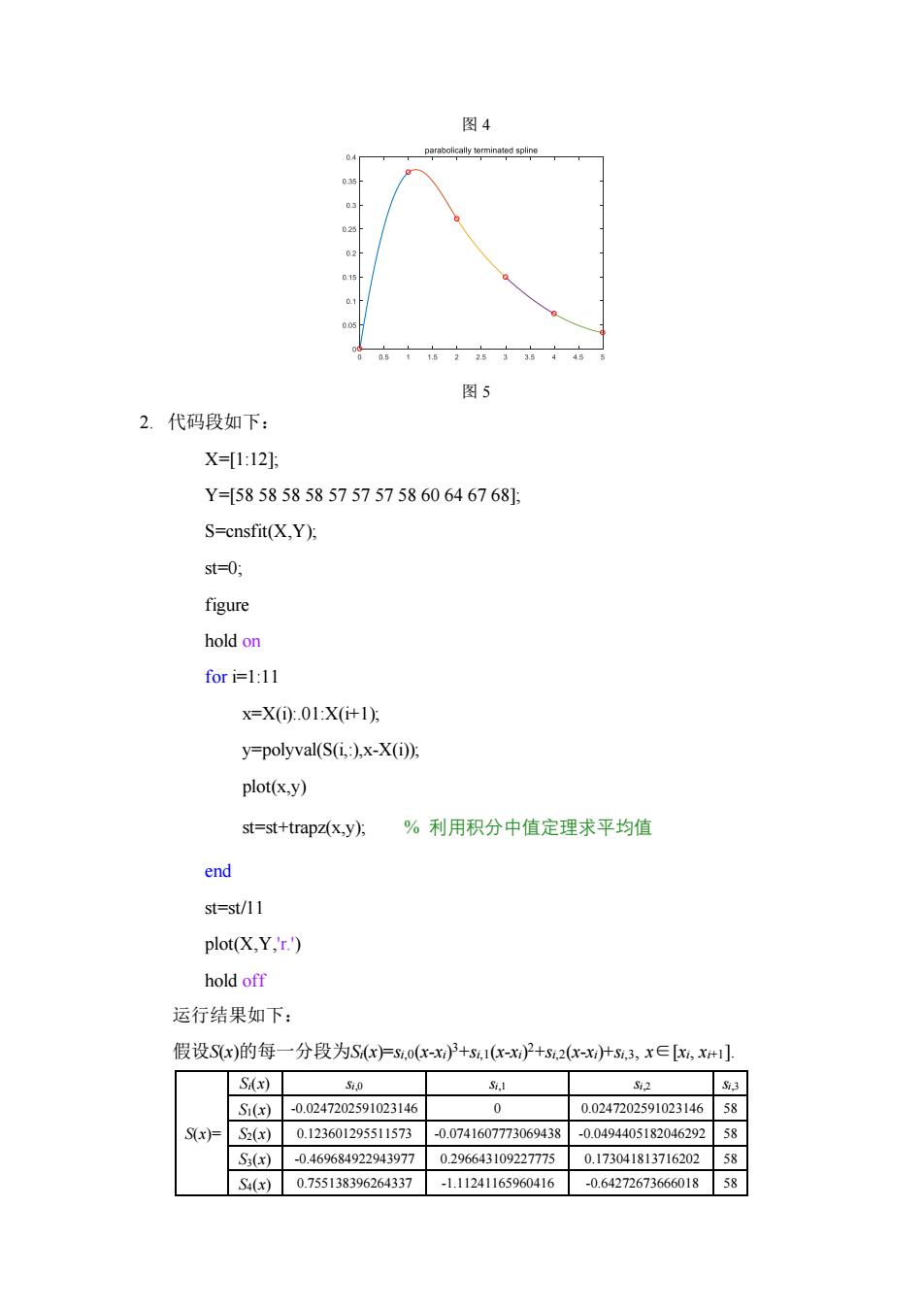
图4 图5 2.代码段如下: X=[1:12 Y=[5858585857575758606467681: S=cnsfit(X,Y方 st=0, figure hold on for i=1:11 x=X0.01:X(it1方 y-polyval(S(i:).x-X(i)) plot(x,y) st-st+trapz(x.y). %利用积分中值定理求平均值 end st=st/11 plot(X.Y.) hold off 运行结果如下: 假设Sx)的每 一分段为Sx.0(x-x3+5z1(xxP+52(x53,x∈,x1 S 52 S1(x) -0.0247202591023146 0 0.0247202591023146 S(x)= S()0.123601295511573 -0.0741607773069438-0.0494405182046292 5 x1-0469649220439770206643109227775 0.173041813716202 58 S(x) 0.755138396264337 -1.11241165960416 -0.6427267366601858
图 4 图 5 2. 代码段如下: X=[1:12]; Y=[58 58 58 58 57 57 57 58 60 64 67 68]; S=cnsfit(X,Y); st=0; figure hold on for i=1:11 x=X(i):.01:X(i+1); y=polyval(S(i,:),x-X(i)); plot(x,y) st=st+trapz(x,y); % 利用积分中值定理求平均值 end st=st/11 plot(X,Y,'r.') hold off 运行结果如下: 假设S(x)的每一分段为Si(x)=si,0(x-xi) 3+si,1(x-xi) 2+si,2(x-xi)+si,3, x∈[xi, xi+1]. S(x)= Si(x) si,0 si,1 si,2 si,3 S1(x) -0.0247202591023146 0 0.0247202591023146 58 S2(x) 0.123601295511573 -0.0741607773069438 -0.0494405182046292 58 S3(x) -0.469684922943977 0.296643109227775 0.173041813716202 58 S4(x) 0.755138396264337 -1.11241165960416 -0.64272673666018 58
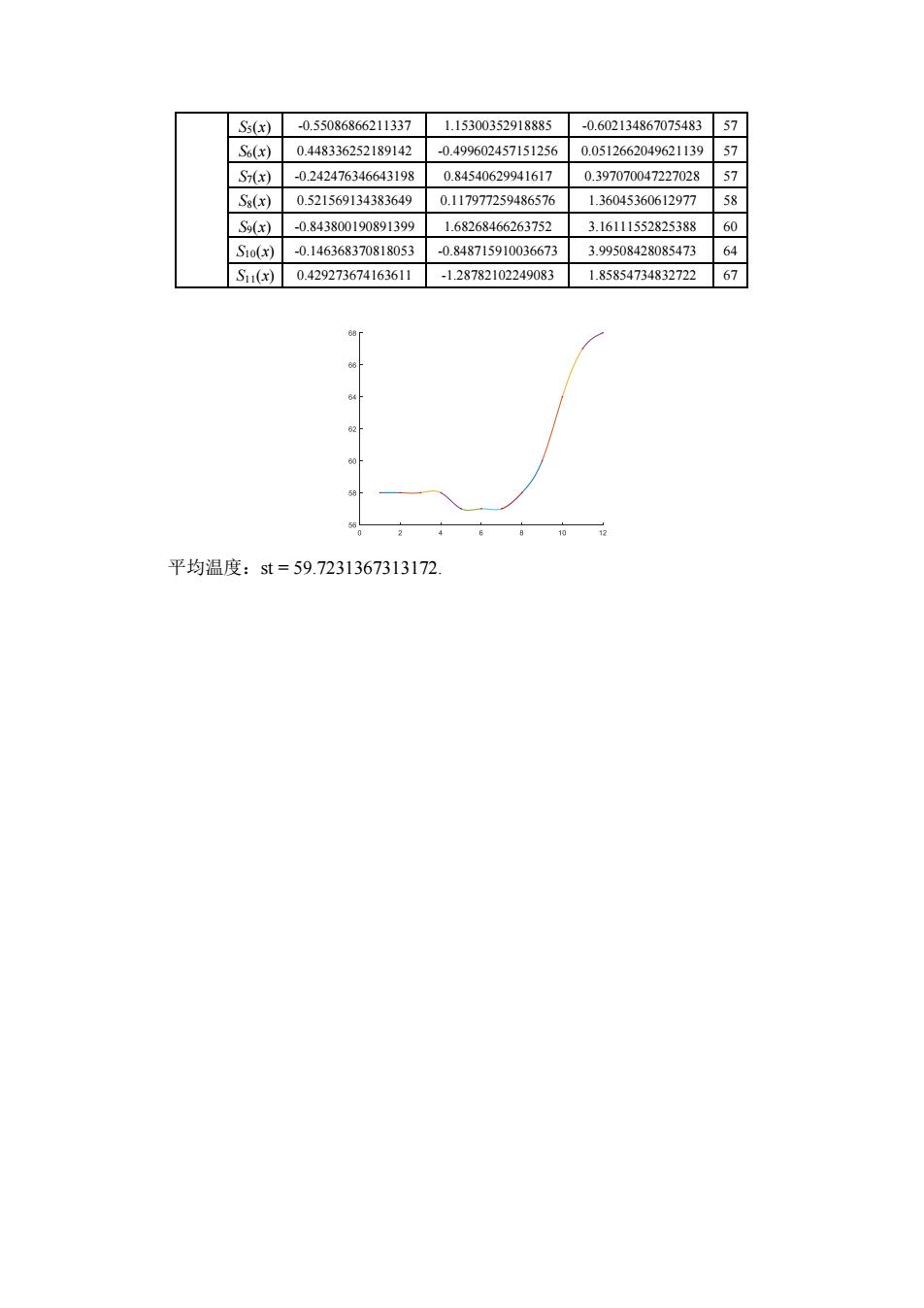
x1-0.550868662113371.15300352918885-0.60213486707548357 .44836252189142 0.49960245715125 0.051266204962113 57 Si(x) -0.242476346643198 0.84540629941617 0.397070047227028 57 0.521569134383649 0.117977259486576 1.36045360612977 S(r) 0843800190891399 16826R466263752 31611152825388 60 Sio(x) 8715910 64 S11()0.429273674163611 -12878210224908 1.85854734832722 67 64 平均温度:st=59.7231367313172
S5(x) -0.55086866211337 1.15300352918885 -0.602134867075483 57 S6(x) 0.448336252189142 -0.499602457151256 0.0512662049621139 57 S7(x) -0.242476346643198 0.84540629941617 0.397070047227028 57 S8(x) 0.521569134383649 0.117977259486576 1.36045360612977 58 S9(x) -0.843800190891399 1.68268466263752 3.16111552825388 60 S10(x) -0.146368370818053 -0.848715910036673 3.99508428085473 64 S11(x) 0.429273674163611 -1.28782102249083 1.85854734832722 67 平均温度:st = 59.7231367313172