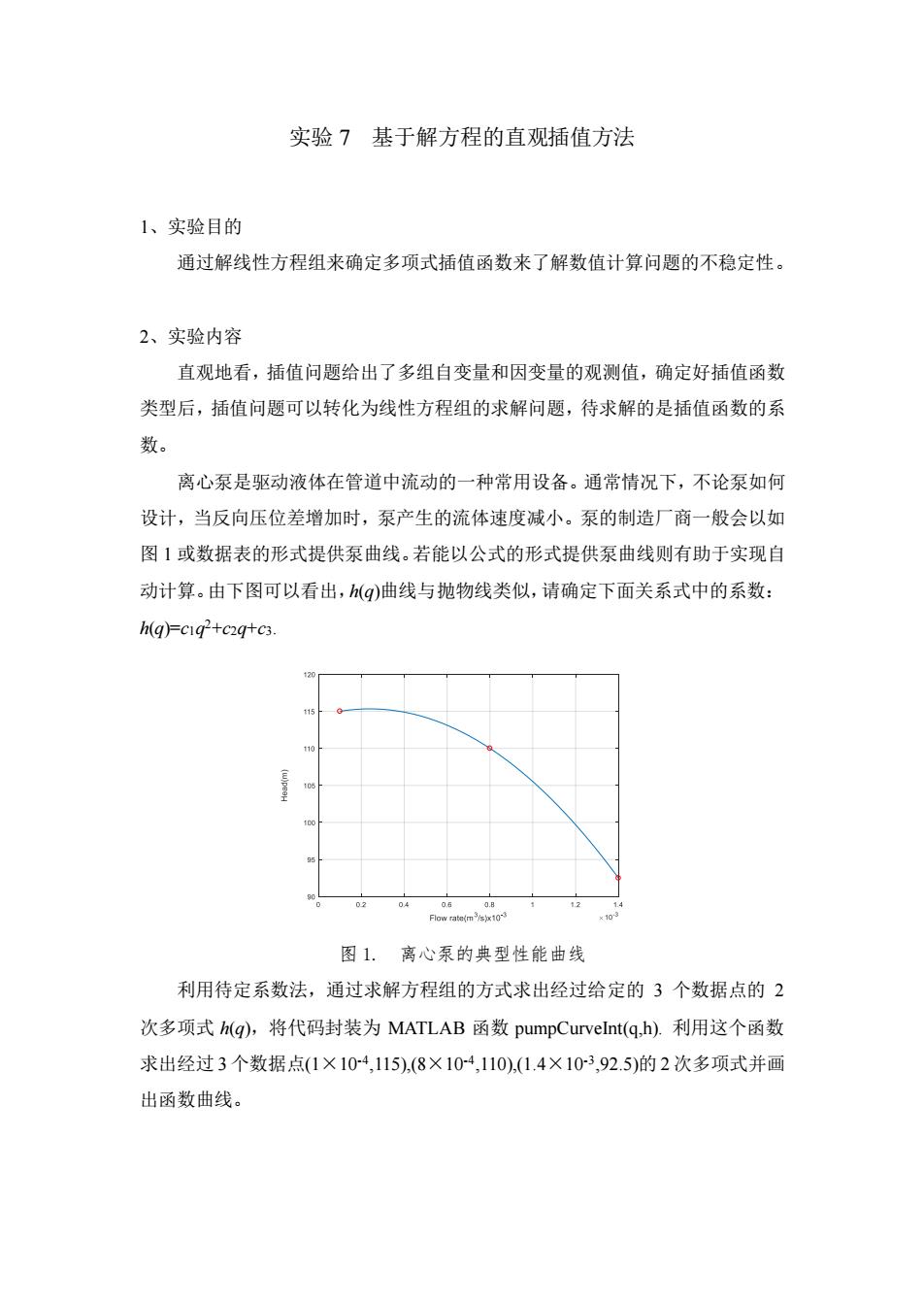
实验7基于解方程的直观插值方法 1、实验目的 通过解线性方程组来确定多项式插值函数来了解数值计算问题的不稳定性。 2、实验内容 直观地看,插值问题给出了多组自变量和因变量的观测值,确定好插值函数 类型后,插值问题可以转化为线性方程组的求解问题,待求解的是插值函数的系 数。 离心泵是驱动液体在管道中流动的一种常用设备。通常情况下,不论泵如何 设计,当反向压位差增加时,泵产生的流体速度减小。泵的制造厂商一般会以如 图1或数据表的形式提供泵曲线。若能以公式的形式提供泵曲线则有助于实现自 动计算。由下图可以看出,M)曲线与抛物线类似,请确定下面关系式中的系数: hq)=cig+czq+cs. 图1.离心泵的典型性能曲线 利用待定系数法,通过求解方程组的方式求出经过给定的3个数据点的2 次多项式h(g),将代码封装为MATLAB函数pumpCurvelnt(q,h).利用这个函数 求出经过3个数据点(1×10-4,115).(8×104,110),(1.4×103,92.5)的2次多项式并画 出函数曲线
实验 7 基于解方程的直观插值方法 1、实验目的 通过解线性方程组来确定多项式插值函数来了解数值计算问题的不稳定性。 2、实验内容 直观地看,插值问题给出了多组自变量和因变量的观测值,确定好插值函数 类型后,插值问题可以转化为线性方程组的求解问题,待求解的是插值函数的系 数。 离心泵是驱动液体在管道中流动的一种常用设备。通常情况下,不论泵如何 设计,当反向压位差增加时,泵产生的流体速度减小。泵的制造厂商一般会以如 图 1 或数据表的形式提供泵曲线。若能以公式的形式提供泵曲线则有助于实现自 动计算。由下图可以看出,h(q)曲线与抛物线类似,请确定下面关系式中的系数: h(q)=c1q 2+c2q+c3. 图 1. 离心泵的典型性能曲线 利用待定系数法,通过求解方程组的方式求出经过给定的 3 个数据点的 2 次多项式 h(q),将代码封装为 MATLAB 函数 pumpCurveInt(q,h). 利用这个函数 求出经过 3 个数据点(1×10-4 ,115),(8×10-4 ,110),(1.4×10-3 ,92.5)的 2 次多项式并画 出函数曲线
3、实验要求 使用之前实验中所编写的求解线性代数方程组的函数来实现。 4、实验习题 1)改写本实验中编写的pumpCurvelnt函数为pumpCurvelnt1函数,使之能够接 受任意长度的输入向量g和h。利用这个改编函数对下表数据进行恰当次数多项 式插值并画出函数曲线。 qm3s)0.00010.000250.00080.0010.0014 m)115114.2110105.592.5 2)修改pumpCurveint函数为pumpCurveInt2函数,使之除了能计算多项式的 系数,还能计算方程组系数矩阵的条件数。利用这个改编函数分别求出上面两题 的系数矩阵的条件数。条件数随着多项式的次数如何改变? 3)使用上题编写的pumpCurvelnt2函数研究输入数据扰动的影响。将第二个h 的值=114.2代换为仁114,重新计算四次插值多项式的系数。令:为扰动数据 所得三次插值多项式的系数,c为原始数据所得多项式的系数。对每个多项式系 数,相对误差(C-c,)/c,是多少?在区间min(g)5qsmax(g)的100个数据点上对两 个四次插值多项式计算()并画图。由扰动数据和原始数据所得到的插值式的? 的最大误差是多少?通过扰动c值导致插值式所得结果h的变化来讨论扰动对实 际问题影响的重要性。 4)将上题中的数据g转化为mhou,重复上题的计算。其中哪个结果改变了? 哪个结果在比例上没有影响?本问题中缩放输入数据的比例有什么好处? 5、实验思考 通过解线性方程组来确定插值函数的方法从数值计算的角度看存在哪些缺点? 如何根据插值问题的自身特征来给出更有效的插值函数构造方法?
3、实验要求 使用之前实验中所编写的求解线性代数方程组的函数来实现。 4、实验习题 1)改写本实验中编写的 pumpCurveInt 函数为 pumpCurveInt1 函数,使之能够接 受任意长度的输入向量 q 和 h。利用这个改编函数对下表数据进行恰当次数多项 式插值并画出函数曲线。 q(m3 /s) 0.0001 0.00025 0.0008 0.001 0.0014 h(m) 115 114.2 110 105.5 92.5 2)修改 pumpCurveInt1 函数为 pumpCurveInt2 函数,使之除了能计算多项式的 系数,还能计算方程组系数矩阵的条件数。利用这个改编函数分别求出上面两题 的系数矩阵的条件数。条件数随着多项式的次数如何改变? 3)使用上题编写的 pumpCurveInt2 函数研究输入数据扰动的影响。将第二个 h 的值 h=114.2 代换为 h=114,重新计算四次插值多项式的系数。令 c ~ 为扰动数据 所得三次插值多项式的系数,c 为原始数据所得多项式的系数。对每个多项式系 数,相对误差 i i i c c )/ c ~( − 是多少?在区间 min(q)≤q≤max(q)的 100 个数据点上对两 个四次插值多项式计算 h(q)并画图。由扰动数据和原始数据所得到的插值式的 h 的最大误差是多少?通过扰动 c 值导致插值式所得结果 h 的变化来讨论扰动对实 际问题影响的重要性。 4)将上题中的数据 q 转化为 m3 /hour,重复上题的计算。其中哪个结果改变了? 哪个结果在比例上没有影响?本问题中缩放输入数据的比例有什么好处? 5、实验思考 通过解线性方程组来确定插值函数的方法从数值计算的角度看存在哪些缺点? 如何根据插值问题的自身特征来给出更有效的插值函数构造方法?