
车南种彩头寻 Numerical Differentiation
Numerical Differentiation

Numerical Differentiation Estimate the derivatives (slope,curvature,etc.) of a function by using the function values at only a set of discrete points Ordinary differential equation (ODE) Partial differential equation (PDE) Represent the function by Taylor polynomials or Lagrange interpolation Evaluate the derivatives of the interpolation polynomial at selected nodal points
Numerical Differentiation ◼ Estimate the derivatives (slope, curvature, etc.) of a function by using the function values at only a set of discrete points ◼ Ordinary differential equation (ODE) ◼ Partial differential equation (PDE) ◼ Represent the function by Taylor polynomials or Lagrange interpolation ◼ Evaluate the derivatives of the interpolation polynomial at selected nodal points
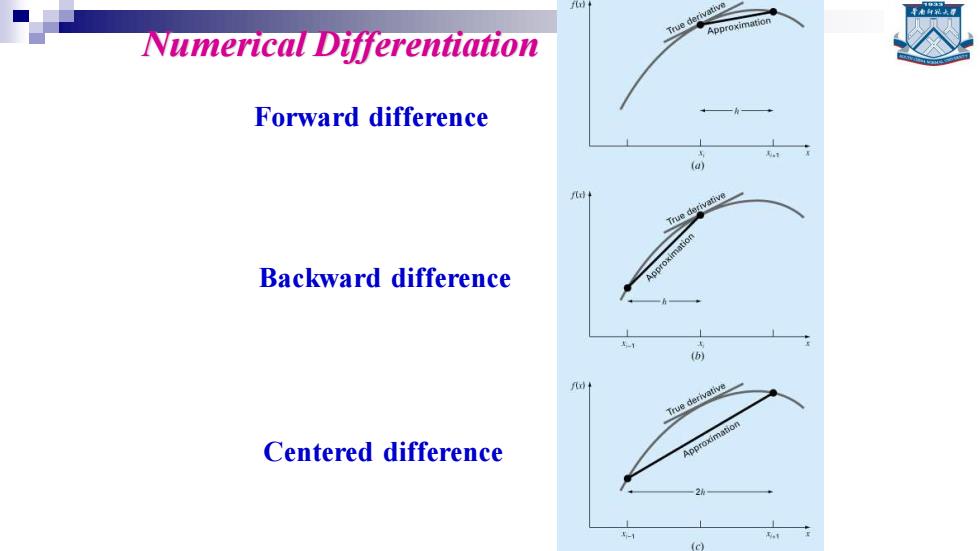
True derivative Approximation Numerical Differentiation Forward difference (a) Backward difference True derivative Centered difference Approximation 2
Forward difference Backward difference Centered difference Numerical Differentiation
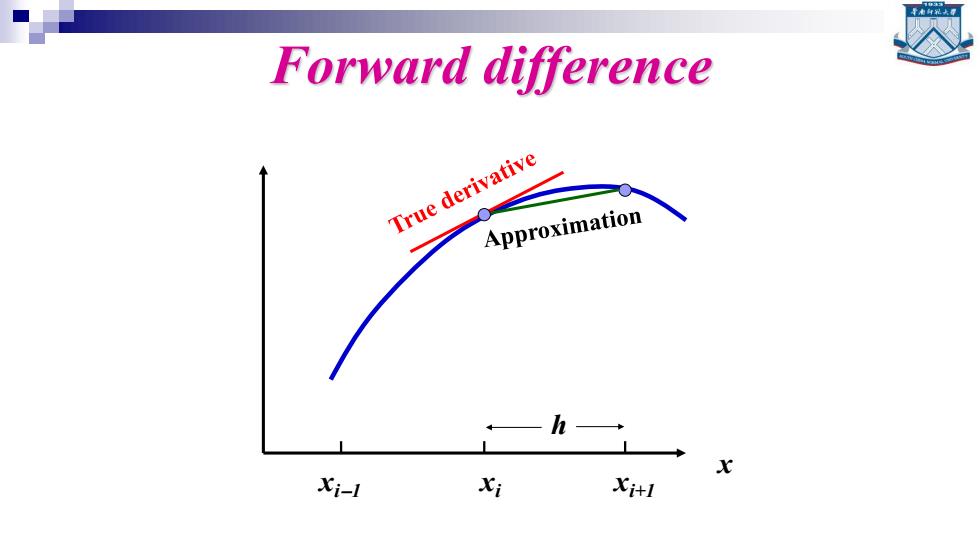
Forward difference True derivative Approximation Xi-1 Xi X+1
Forward difference xi−1 xi xi+1 x h
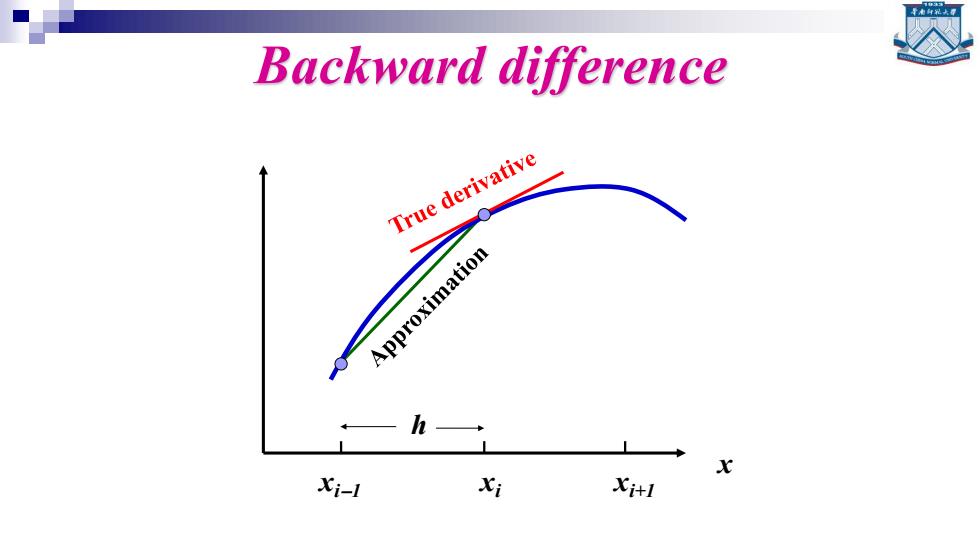
Backward difference True derivative Approximation Xi-1 xi Xi+1
Backward difference xi−1 xi xi+1 x h
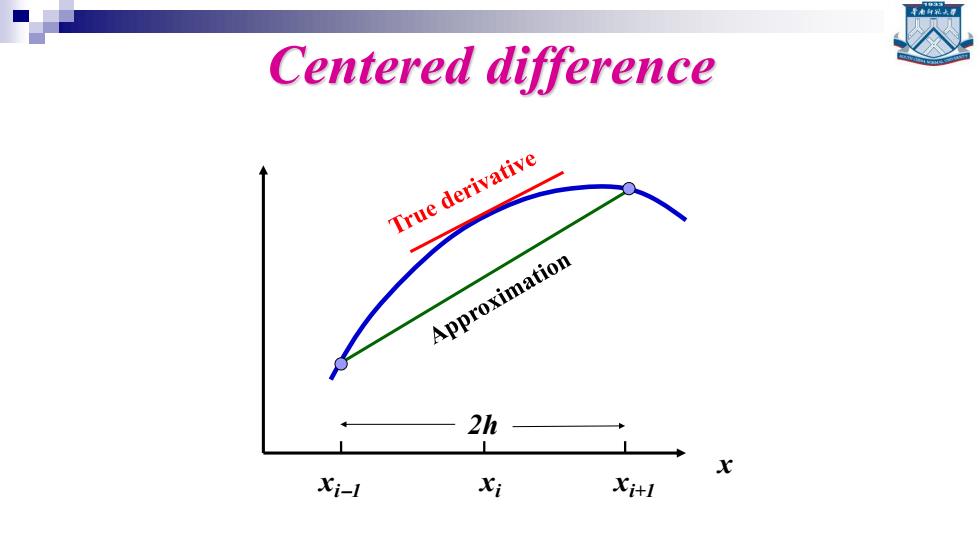
Centered difference True derivative Approximation 2h Xi-1 Xi Xi+1
Centered difference xi−1 xi xi+1 x 2h
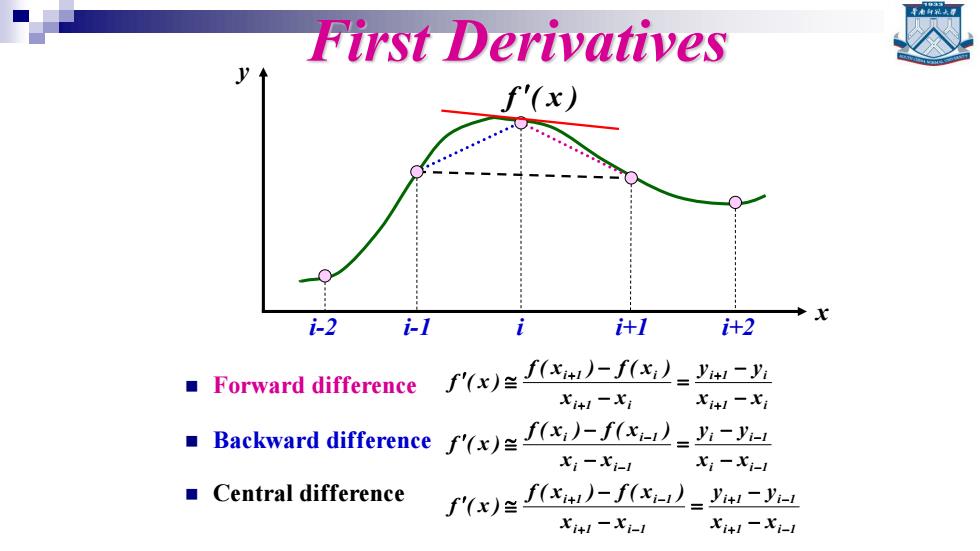
First Derivatives f'(x) i-2 -1 i计l i+2 ■Forward difference 了x)f4小-fs-4-y 七+1-X, xi41- Backward difference x))f( Xi-Xi-1 Xi-xi-1 ■Central difference f(x)f(xu)-f(x)=yu-y i+1-i-1 Xi+l-Xi-1
First Derivatives ◼ Forward difference ◼ Backward difference ◼ Central difference f ( x ) i-2 i-1 i i+1 i+2 i 1 i 1 i 1 i 1 i 1 i 1 i 1 i 1 i i 1 i i 1 i i 1 i i 1 i 1 i i 1 i i 1 i i 1 i x x y y x x f ( x ) f ( x ) f ( x ) x x y y x x f ( x ) f ( x ) f ( x ) x x y y x x f ( x ) f ( x ) f ( x ) + − + − + − + − − − − − + + + + − − = − − − − = − − − − = − − x y

Truncation Errors Uniform grid spacing h2 fx)=x,+)=x+(+2∫x,+x+ h2 d=0-)=0代-x+2x)了R fonvard:P()f(a)() O h 2 backward:frx))=f)-f小+gfr5,) 0(h) h central f(x)=f)-f( f"(5) 02) 2h 6
Truncation Errors ◼ Uniform grid spacing = − = − + − + = + = + + + + − + f ( x ) 3! h f ( x ) 2! h f ( x ) f ( x h ) f ( x ) hf ( x ) f ( x ) 3! h f ( x ) 2! h f ( x ) f ( x h ) f ( x ) hf ( x ) i 3 i 2 i 1 i i i i 3 i 2 i 1 i i i − − = + − = − − = + − − + ( ) ) ( ) ( ) : ( ) ( ) ( ) ( ) : ( ) ( ) ( ) ( ) : ( ) 2 3 2 i 1 i 1 i 2 i i 1 i 1 i 1 i i f O(h 6 h 2h f x f x central f x f O(h) 2 h h f x f x backward f x f O(h) 2 h h f x f x forward f x
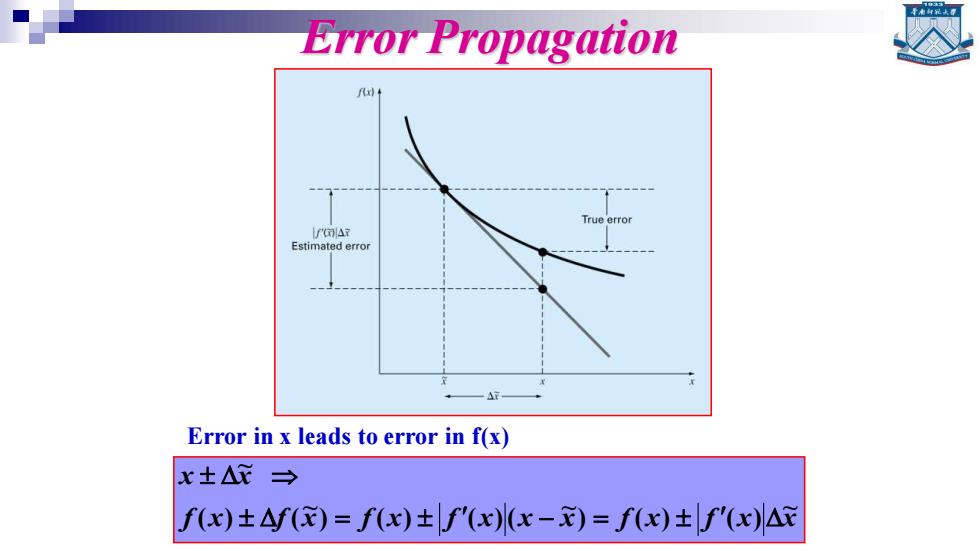
Error Propagation f ImAr Estimated error Error in x leads to error in f(x) x土△→ fx)±△f(E)=fx)±f'(x)x-)=f(x)±f'(x)△c
Error Propagation f x f x f x f x x x f x f x x x x ~ ) ( ) ( ) ~ ) ( ) ( )( ~ ( ) ( ~ = − = Error in x leads to error in f(x)

Total Numerical Error Point of diminishing returns Total error Truncation error Round-off error log step size Trade-off between truncation and round-off errors
Trade-off between truncation and round-off errors Total Numerical Error