
《常微分方程》课程教学大纲 一、课程基本信息 课程代码:16010903 课程名称:常微分方程 英文名称:Ordinary differential equation 课程类别:专业课 学 时:54 学分:3 适用对象:数学类本科生 考核方式:考试 先修课程: 数学分析、高等代数 二、课程简介 常微分方程是高等师范院校数学系各专业的重要基础课,也是应用性很强的一门 数学课。微分方程课的目的一方面使学生学好作为数学基础的常微分方程课,以便为 后行课数理方程、微分几何、泛函分析作好准备;另一方面培养学生理论联系实际和 分析问题解决问题的能力。 Ordinary differential equation is an important basic course of mathematics department in Normal University,and it is also a mathematics course with strong application.On the one hand,the purpose of differential equation course is to enable students to learn ordinary differential equation well, which is the basis of mathematics,so as to prepare for the later courses of mathematical equation,differential geometry and functional analysis:on the other hand,to cultivate students'ability of integrating theory with practice and analyzing and solving problems 三、课程性质与教学目的 1、本课程是数学类专业的基础之一,授课对象为本科数学类专业学生。在讲授和 学习时,应注重提高学生分析问题和解决问题的能力,培养学生良好的逻辑思维习惯, 让学生掌握全面考虑问题的思维方法,这将有助于学生们顺利地学习其他专业理论 课
1 《常微分方程》课程教学大纲 一、课程基本信息 课程代码:16010903 课程名称:常微分方程 英文名称: Ordinary differential equation 课程类别: 专业课 学 时: 54 学 分: 3 适用对象: 数学类本科生 考核方式: 考试 先修课程: 数学分析、高等代数 二、课程简介 常微分方程是高等师范院校数学系各专业的重要基础课,也是应用性很强的一门 数学课。微分方程课的目的一方面使学生学好作为数学基础的常微分方程课,以便为 后行课数理方程、微分几何、泛函分析作好准备;另一方面培养学生理论联系实际和 分析问题解决问题的能力。 Ordinary differential equation is an important basic course of mathematics department in Normal University, and it is also a mathematics course with strong application. On the one hand, the purpose of differential equation course is to enable students to learn ordinary differential equation well, which is the basis of mathematics, so as to prepare for the later courses of mathematical equation, differential geometry and functional analysis; on the other hand, to cultivate students' ability of integrating theory with practice and analyzing and solving problems. 三、课程性质与教学目的 1、本课程是数学类专业的基础之一,授课对象为本科数学类专业学生。在讲授和 学习时,应注重提高学生分析问题和解决问题的能力,培养学生良好的逻辑思维习惯, 让学生掌握全面考虑问题的思维方法,这将有助于学生们顺利地学习其他专业理论 课

Teaching purpose and requirements:Master the basic idea,content and method of ordinary differential equation,master the primary solution of first-order and high-order differential equation,and the solution of constant coefficient linear differential equation (systems).Through the teaching of ordinary differential equation,the students can master the basic process and method of establishing ordinary differential equation model,and cultivate the students'ability of analyzing and solving problems. 2.The main contents of this course include:(1)First-Order Differential Equations:(2)Mathematical Models:(3)Linear Second-Order Equations:(4) Introduction to Systems and Phase Plane Analysis;(5)Theory of Higher-Order Linear Differential Equations:(6)Laplace Transforms:(7)Series Solutions of Differential Equations:(8)Matrix Methods for Linear Systems. 3.This course is mainly taught in class,supplemented by discussion and guidance,and combines classroom practice with homework 4、在制定本教学大纲时,为了明确对教学大纲中所列具体内容的要求程度,将 本要求分为由低到高的三个等级,即对概念和理论性的知识,由低到高分别用“知道” “了解”、“理解”三级区分,对运算、方法和应用方面的知识,由低到高分别用“会 或能”、“掌握”、“熟练掌握”三级区分。 5、让学生体会到数学的美妙与乐趣:激发学生的求知欲和探求科学知识的兴趣: 培养学生克服困难的品质:培养学生正确的价值观和积极向上的思想,鼓励学生努力 实现自身理想。 四、教学内容及要求 第一章Introduction (一)目的与要求 1.向学生介绍微分方程的轮廓 2.学习基本概念 (二)教学内容 1.主要内容 某些物理过程的数学模型;微分方程的背景。 2.基本概念和知识点 3.常微分方程,偏微分方程,阶、线性、非线性,特解,通解,初始条 2
2 Teaching purpose and requirements: Master the basic idea, content and method of ordinary differential equation, master the primary solution of first-order and high-order differential equation, and the solution of constant coefficient linear differential equation (systems). Through the teaching of ordinary differential equation, the students can master the basic process and method of establishing ordinary differential equation model, and cultivate the students' ability of analyzing and solving problems. 2、The main contents of this course include: ⑴ First-Order Differential Equations;⑵ Mathematical Models;⑶ Linear Second-Order Equations;(4) Introduction to Systems and Phase Plane Analysis;(5) Theory of Higher-Order Linear Differential Equations;(6) Laplace Transforms;(7) Series Solutions of Differential Equations;(8) Matrix Methods for Linear Systems。 3、This course is mainly taught in class, supplemented by discussion and guidance, and combines classroom practice with homework。 4、在制定本教学大纲时,为了明确对教学大纲中所列具体内容的要求程度,将 本要求分为由低到高的三个等级,即对概念和理论性的知识,由低到高分别用“知道”、 “了解”、“理解”三级区分,对运算、方法和应用方面的知识,由低到高分别用“会 或能”、“掌握”、“熟练掌握”三级区分。 5、让学生体会到数学的美妙与乐趣;激发学生的求知欲和探求科学知识的兴趣; 培养学生克服困难的品质;培养学生正确的价值观和积极向上的思想,鼓励学生努力 实现自身理想。 四、教学内容及要求 第一章 Introduction (一)目的与要求 1.向学生介绍微分方程的轮廓 2.学习基本概念 (二)教学内容 1.主要内容 某些物理过程的数学模型;微分方程的背景。 2.基本概念和知识点 3.常微分方程,偏微分方程,阶、线性、非线性,特解,通解,初始条

件,定解问题,一阶微分方程的几何意义,方向场,积分曲线。 第二章First--Order Differential Equations (一)目的与要求 1.要求学生学完本章后能迅速区分方程的类型,并根据方程的类型用相 应的方法熟练地求出通解: 2.掌握变量变换与变量分离方程、线性方程与常数变易法、恰当方程与 积分因子等知识: (二)教学内容 1.主要内容 (1)自由落体运动描述: (2)变量分离方程与变量变换; (3)线性方程与常数变易法: (④)恰当方程与积分因子: (5)替换和变换。 2.基本概念和知识点 变量变换与变量分离方程、线性方程与常数变易法、恰当方程与积分因 子,替换和变换。 第三章Mathematical Models (一)目的与要求 1.掌握微分方程数学模型 2.培养学生理论联系实际的能力 (二)教学内容 1.主要内容 数学模型:计算分析」 2.基本概念和知识点 水箱模型,人口模型 3.问题与应用 运用常微分方程研究水箱进出水和人口增长等问题。 第四章Linear Second--Order Equations (一)目的与要求 1.要求熟练的掌握解的基本定理和常系数方程的解法 2.培养学生透过现象看本质的能力 (二)教学内容 1.主要内容 3
3 件,定解问题,一阶微分方程的几何意义,方向场,积分曲线。 第二章 First-Order Differential Equations (一) 目的与要求 1.要求学生学完本章后能迅速区分方程的类型,并根据方程的类型用相 应的方法熟练地求出通解; 2.掌握变量变换与变量分离方程、线性方程与常数变易法、恰当方程与 积分因子等知识; (二) 教学内容 1.主要内容 (1)自由落体运动描述; (2)变量分离方程与变量变换; (3)线性方程与常数变易法; (4)恰当方程与积分因子; (5)替换和变换。 2.基本概念和知识点 变量变换与变量分离方程、线性方程与常数变易法、恰当方程与积分因 子,替换和变换。 第三章 Mathematical Models (一) 目的与要求 1.掌握微分方程数学模型 2.培养学生理论联系实际的能力 (二) 教学内容 1.主要内容 数学模型;计算分析。 2.基本概念和知识点 水箱模型,人口模型。 3.问题与应用 运用常微分方程研究水箱进出水和人口增长等问题。 第四章 Linear Second-Order Equations (一) 目的与要求 1.要求熟练的掌握解的基本定理和常系数方程的解法 2.培养学生透过现象看本质的能力 (二) 教学内容 1.主要内容

弹簧振子模型:齐次线性方程:具有复根的特征方程:非齐次方程。 2.基本概念和知识点 齐次线性方程:具有复根的特征方程;非齐次方程:待定系数法。 第五章Introduction to Systems and Phase Plane Analysis (一)目的与要求 1.系统和相平面分析简介 2.培养学生不畏困难的品质 (二)教学内容 1.主要内容 系统和相平面分析。 2.基本概念和知识点 互联储液罐;微分算子。 第六章Theory of Higher-Order Linear Differential Equations (一)目的与要求 1,掌握线性微分方程的基本理论和常系数齐次线性微分方程的求解 2.培养学生知识迁移的能力以及与时俱进的思想 (二)教学内容 1.主要内容 线性微分方程的基本理论:常系数齐次线性微分方程。 2.基本概念和知识点 常系数,变系数,标准型,微分算子,朗斯基行列式,线性相关,线性 无关,通解,特征方程。 第七和第八章Laplace Transforms Series Solutions of Differential Equations (一)目的与要求 1.了解拉普拉斯变换和幂级数解法 2.介绍微分方程前沿研究成果,鼓励学生继续深造,培养学生积极上进 的思想 (二)教学内容 1.主要内容 拉普拉斯变换概念性质;幂级数基本解法。 2.基本概念和知识点 拉普拉斯变换,泰勒展式,幂级数,解析函数。 第九章Matrix Methods for Linear Systems (一)目的与要求
4 弹簧振子模型;齐次线性方程;具有复根的特征方程;非齐次方程。 2.基本概念和知识点 齐次线性方程;具有复根的特征方程;非齐次方程;待定系数法。 第五章 Introduction to Systems and Phase Plane Analysis (一) 目的与要求 1.系统和相平面分析简介 2.培养学生不畏困难的品质 (二) 教学内容 1.主要内容 系统和相平面分析。 2.基本概念和知识点 互联储液罐;微分算子。 第六章 Theory of Higher-Order Linear Differential Equations (一) 目的与要求 1.掌握线性微分方程的基本理论和常系数齐次线性微分方程的求解 2.培养学生知识迁移的能力以及与时俱进的思想 (二) 教学内容 1.主要内容 线性微分方程的基本理论;常系数齐次线性微分方程。 2.基本概念和知识点 常系数,变系数,标准型,微分算子,朗斯基行列式,线性相关,线性 无关,通解,特征方程。 第七和第八章 Laplace Transforms Series Solutions of Differential Equations (一) 目的与要求 1.了解拉普拉斯变换和幂级数解法 2.介绍微分方程前沿研究成果,鼓励学生继续深造,培养学生积极上进 的思想 (二) 教学内容 1.主要内容 拉普拉斯变换概念性质;幂级数基本解法。 2.基本概念和知识点 拉普拉斯变换,泰勒展式,幂级数,解析函数。 第九章 Matrix Methods for Linear Systems (一) 目的与要求
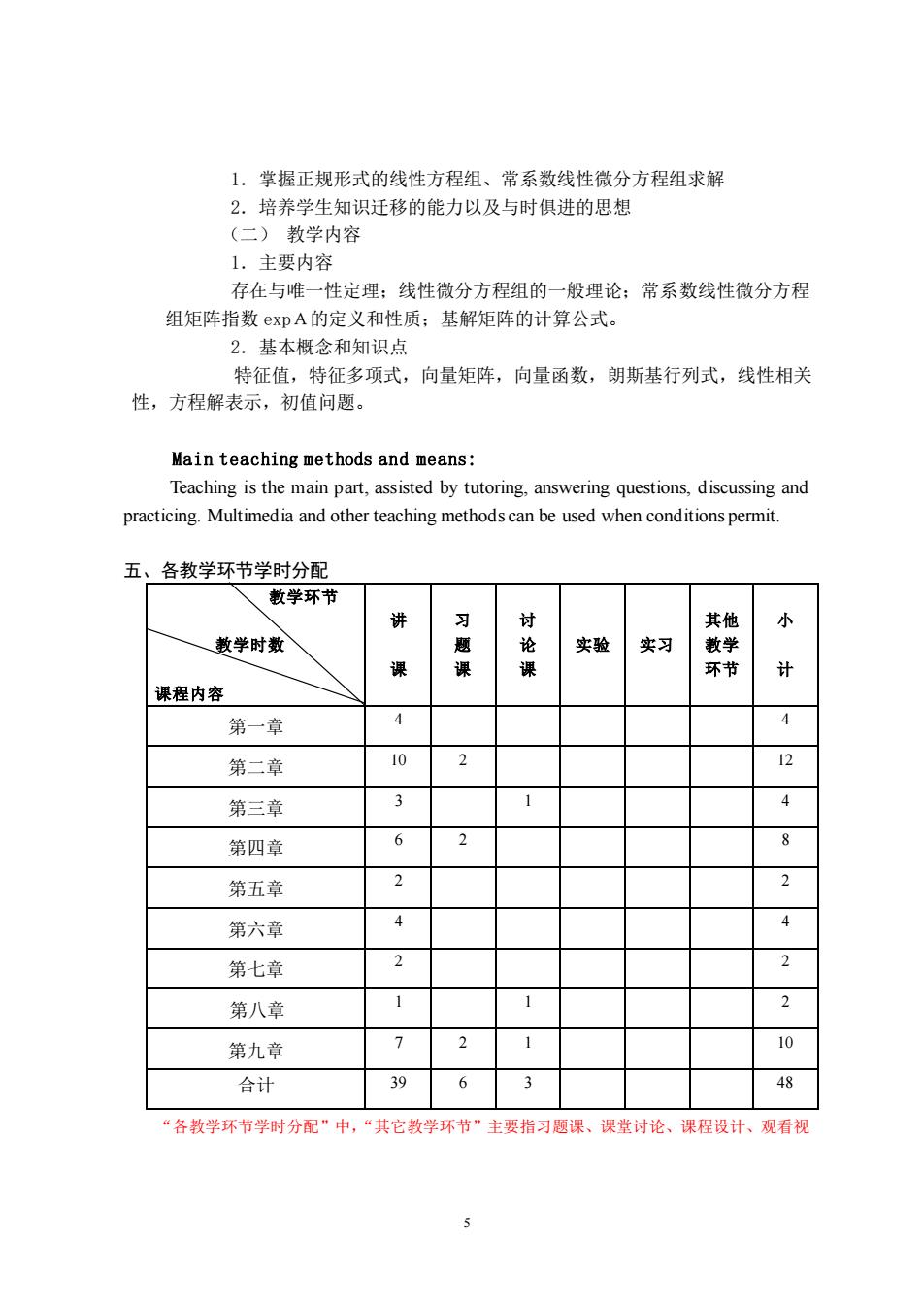
1.掌握正规形式的线性方程组、常系数线性微分方程组求解 2.培养学生知识迁移的能力以及与时俱进的思想 (二)教学内容 1.主要内容 存在与唯一性定理:线性微分方程组的一般理论:常系数线性微分方程 组矩阵指数expA的定义和性质;基解矩阵的计算公式。 2.基本概念和知识点 特征值,特征多项式,向量矩阵,向量函数,朗斯基行列式,线性相关 性,方程解表示,初值问题。 Main teaching methods and means: Teaching is the main part,assisted by tutoring,answering questions,discussing and practicing.Multimedia and other teaching methods can be used when conditions permit. 五、各教学环节学时分配 教学环节 讲 习 其他 小 教学时数 实验 实习 教学 课 课 课 环节 计 课程内容 第一章 4 第二章 10 2 12 第三章 3 1 4 第四章 6 3 8 第五章 2 2 第六章 4 4 第七章 2 第八章 1 1 2 第九章 > 2 10 合计 39 6 3 48 “各教学环节学时分配”中,“其它教学环节”主要指习题课、课堂讨论、课程设计、观看视
5 1.掌握正规形式的线性方程组、常系数线性微分方程组求解 2.培养学生知识迁移的能力以及与时俱进的思想 (二) 教学内容 1.主要内容 存在与唯一性定理;线性微分方程组的一般理论;常系数线性微分方程 组矩阵指数 expA的定义和性质;基解矩阵的计算公式。 2.基本概念和知识点 特征值,特征多项式,向量矩阵,向量函数,朗斯基行列式,线性相关 性,方程解表示,初值问题。 Main teaching methods and means: Teaching is the main part, assisted by tutoring, answering questions, discussing and practicing. Multimedia and other teaching methods can be used when conditions permit. 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 实习 其他 教学 环节 小 计 第一章 4 4 第二章 10 2 12 第三章 3 1 4 第四章 6 2 8 第五章 2 2 第六章 4 4 第七章 2 2 第八章 1 1 2 第九章 7 2 1 10 合计 39 6 3 48 “各教学环节学时分配”中,“其它教学环节”主要指习题课、课堂讨论、课程设计、观看视

频、现场参观等教学环节。 六、课程考核 (一)考核方式 考试 (二)成绩构成 平时成绩占比:40%期未考试占比:60% 七、推荐教材和教学参考资源 [1]王高雄等编。常微分方程(第三版),北京:高等教育出版社,2001年。 [2]丁同仁,李承治编.常微分方程讲义,北京:高等教育出版社,2002年。 [3]叶彦谦编。常微分方程讲义.北京:人民教育出版社,1979年。 八、其他说明 大纲修订人:古勇毅 修订日期:2020年12月 大纲审定人:刘国刚 审定日期:2020年12月
6 频、现场参观等教学环节。 六、课程考核 (一)考核方式 考试 (二)成绩构成 平时成绩占比:40% 期末考试占比:60% 七、推荐教材和教学参考资源 [1] 王高雄等编. 常微分方程(第三版),北京:高等教育出版社,2001 年。 [2] 丁同仁,李承治编. 常微分方程讲义,北京:高等教育出版社,2002 年。 [3] 叶彦谦编. 常微分方程讲义. 北京:人民教育出版社,1979 年。 八、其他说明 大纲修订人:古勇毅 修订日期:2020 年 12 月 大纲审定人:刘国刚 审定日期:2020 年 12 月