
《偏微分方程》课程教学大纲 一、课程基本信息 课程代码:16002102 课程名称:偏微分方程 英文名称:Partial Differential Equations 课程类别:专业课 学 时:32 适用对象:数学与应用数学 考核方式:考查 先修课程! 数学分析、常微分方程、高等代数 二、课程简介 偏微分方程是以建立数学模型、进行理论分析和解释客观现象并进而解决实 际问题为内容的一门数学分支学科,是现代数学的一个重要分支。它在微分几何、 物理学、计算数学和计算机图形学、金融数学等学科中都有许多重要应用。本课 程主要内容包括:偏微分方程的基本概念,二阶方程的特征理论和分类,分离变 量法,双曲型、抛物型及椭圆型方程的求解方法及基本理论。通过本课程的学习 使学生初步认识如何从实际问题出发建立微分方程模型,培养学生分析问题和解 决某些实际问题的能力,为日后的学习和工作打下坚实的基础,提供强有力的工 具。 Partial differential equation is a branch of mathematics that establishes mathematical models,analyzes and interprets objective phenomena and then solves practical problems,is an important branch of modem mathematics.It also has many important applications in differential geometry,physics,computational mathematics and computer graphics,financial mathematics and other disciplines.The main contents of this course include:the basic concept of partial differential equation,the characteristic theory and classification of the second order equations,the method of separation of variables,the methods of solving hyperbolic,parabolic and elliptic equations and the basic theory of them.Through learing of this course makes students to know how to establish a differential equation model starting from the practical problems,to cultivate students'ability to analyze problems and solve some practical problems,lay a solid foundation for future study and work and provide a powerful tool
1 《偏微分方程》课程教学大纲 一、课程基本信息 课程代码: 16002102 课程名称: 偏微分方程 英文名称: Partial Differential Equations 课程类别: 专业课 学 时: 32 学 分: 2 适用对象: 数学与应用数学 考核方式: 考查 先修课程: 数学分析、常微分方程、高等代数 二、课程简介 偏微分方程是以建立数学模型、进行理论分析和解释客观现象并进而解决实 际问题为内容的一门数学分支学科,是现代数学的一个重要分支。它在微分几何、 物理学、计算数学和计算机图形学、金融数学等学科中都有许多重要应用。本课 程主要内容包括:偏微分方程的基本概念,二阶方程的特征理论和分类,分离变 量法,双曲型、抛物型及椭圆型方程的求解方法及基本理论。通过本课程的学习 使学生初步认识如何从实际问题出发建立微分方程模型,培养学生分析问题和解 决某些实际问题的能力,为日后的学习和工作打下坚实的基础,提供强有力的工 具。 Partial differential equation is a branch of mathematicsthat establishes mathematical models, analyzes and interprets objective phenomena and then solves practical problems, is an important branch of modern mathematics. It also has many important applications in differential geometry, physics, computational mathematics and computer graphics, financial mathematics and other disciplines. The main contents of this course include: the basic concept of partial differential equation, the characteristic theory and classification of the second order equations, the method of separation of variables, the methods of solving hyperbolic,parabolic and elliptic equations and the basic theory of them. Through learning of this course makes students to know how to establish a differential equation model starting from the practical problems, to cultivate students' ability to analyze problems and solve some practical problems, lay a solid foundation for future study and work and provide a powerful tool

三、课程性质与教学目的 课程性质:专业选修 教学目的:偏微分方程是数学专业的一门重要专业课程。它的理论和方法,对于 其他数学学科、物理、力学及工程技术中的某些问题,都有广泛的应用。通过本 课程的学习,使学生正确理解偏微分方程的基本概念,掌握基本理论和基本方法, 并为进一步了解和学习现代偏微分方程的有关内容提供帮助。同时培养学生分析 问颗和解决某些实际问顺的能力。此外,在学习本课程的讨过程中,使学牛了解偏 微分方程在我国的发展历史、现状以及在国防建设方面所取得的巨大成就,让学 生感受到民族的白豪感和对中国文化的认同成,激昆强列的民族青任感。让学中 在课堂上不仅可以学到知识,还可以开拓境界,熏陶心灵,引导学生树立正确的 世界观、人生观和价值观,更好地为学生成长服务。 四、教学内容及要求 第一章方程的导出及定解问题的提法 (一)目的与要求 1.通过介绍偏微分方程在我国的发展历史、现状和用途以及一些偏微分方 程领域的国内著名数学家的事迹,向学生传递榜样的力量,以数学家的品 格与成就激发学生的学习兴趣,坚定拼搏的信念。 2.理解线性偏微分方程和非线性偏微分方程的概念。 3.了解几个经典的偏微分方程的导出 4.了解偏微分方程定解问题的提法。 〖重点与难点〗 1.本章的重点内容:偏微分方程的基本概念,定解问题的提法 2.本章的难点内容:几个经典的方程的导出。 (二)教学内容 第一节基本概念 1.主要内容 1.1偏微分方程简介 1.2偏微分方程的基本概念 2.基本概念和知识点 什么是偏微分方程,偏微分方程的解和阶,线性和非线性偏微分方程 3.问题与应用 问题:拟线性偏微分方程和半线性偏微分方程的区别?
2 三、课程性质与教学目的 课程性质:专业选修 教学目的:偏微分方程是数学专业的一门重要专业课程。它的理论和方法,对于 其他数学学科、物理、力学及工程技术中的某些问题,都有广泛的应用。通过本 课程的学习,使学生正确理解偏微分方程的基本概念,掌握基本理论和基本方法, 并为进一步了解和学习现代偏微分方程的有关内容提供帮助。同时培养学生分析 问题和解决某些实际问题的能力。此外,在学习本课程的过程中,使学生了解偏 微分方程在我国的发展历史、现状以及在国防建设方面所取得的巨大成就,让学 生感受到民族的自豪感和对中国文化的认同感,激起强烈的民族责任感。让学生 在课堂上不仅可以学到知识,还可以开拓境界,熏陶心灵,引导学生树立正确的 世界观、人生观和价值观,更好地为学生成长服务。 四、教学内容及要求 第一章 方程的导出及定解问题的提法 (一)目的与要求 1. 通过介绍偏微分方程在我国的发展历史、现状和用途以及一些偏微分方 程领域的国内著名数学家的事迹,向学生传递榜样的力量,以数学家的品 格与成就激发学生的学习兴趣,坚定拼搏的信念。 2. 理解线性偏微分方程和非线性偏微分方程的概念。 3. 了解几个经典的偏微分方程的导出。 4. 了解偏微分方程定解问题的提法。 〖重点与难点〗 1. 本章的重点内容:偏微分方程的基本概念,定解问题的提法。 2. 本章的难点内容:几个经典的方程的导出。 (二)教学内容 第一节 基本概念 1. 主要内容 1.1 偏微分方程简介 1.2 偏微分方程的基本概念 2. 基本概念和知识点 什么是偏微分方程,偏微分方程的解和阶,线性和非线性偏微分方程, 3. 问题与应用 问题:拟线性偏微分方程和半线性偏微分方程的区别?

第二节几个经典方程 1.主要内容 弦振动方程、膜振动方程、热传导方程、Laplace方程的推导 2.基本概念和知识点 3.问题与应用 应用:初步了解用偏微分方程建立实际问题的数学模型 第三节定解问题 1.主要内容 定解问题的提法,三类典型的边界条件,适定性 2.基本概念与知识点 3.问题与应用 问题:什么样的边界条件才是合适的边界条件? (三)思考与实践 勤学多练。着重理解偏微分方程的阶、线性和非线性的概念。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第二章二阶方程的特征理论与分类 (一)目的与要求 1了解二阶线性方程的特征理论 2.了解二阶线性方程的分类。 3.掌握双曲型、抛物型和椭圆型偏微分方程的标准型 【重点与难点】 1.本章的重点内容:辨别方程的类型,常系数的双曲型、抛物型和椭圆型 偏微分方程的标准型。 2.本章的难点内容:化多个自变量的二阶方程为标准型。 (二)教学内容 第一节二阶方程的特征 1.主要内容 两个自变量的二阶拟线性偏微分方程的特征,多个自变量的二阶线性偏微 分方程的特征 2.基本概念和知识点 特征曲线,特征曲面,特征方程 3
3 第二节 几个经典方程 1. 主要内容 弦振动方程、膜振动方程、热传导方程、Laplace 方程的推导 2. 基本概念和知识点 3. 问题与应用 应用:初步了解用偏微分方程建立实际问题的数学模型 第三节 定解问题 1. 主要内容 定解问题的提法,三类典型的边界条件,适定性 2. 基本概念与知识点 3. 问题与应用 问题:什么样的边界条件才是合适的边界条件? (三)思考与实践 勤学多练。着重理解偏微分方程的阶、线性和非线性的概念。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第二章 二阶方程的特征理论与分类 (一)目的与要求 1. 了解二阶线性方程的特征理论。 2. 了解二阶线性方程的分类。 3. 掌握双曲型、抛物型和椭圆型偏微分方程的标准型。 〖重点与难点〗 1. 本章的重点内容:辨别方程的类型,常系数的双曲型、抛物型和椭圆型 偏微分方程的标准型。 2. 本章的难点内容:化多个自变量的二阶方程为标准型。 (二)教学内容 第一节 二阶方程的特征 1. 主要内容 两个自变量的二阶拟线性偏微分方程的特征,多个自变量的二阶线性偏微 分方程的特征 2. 基本概念和知识点 特征曲线,特征曲面,特征方程

3.问题与应用 问题:为什么当初始数据在特征曲线上时,一般来说定解问题是无解的, 若有解就一定不唯一? 第二节二阶方程的分类 1.主要内容 两个自变量的二阶线性偏微分方程的分类,主部具有常系数的多个自变量 的二阶线性偏微分方程的分类 2.基本概念和知识点 概念:判别式,特征二次型,双曲型、抛物型、椭圆型偏微分方程, 知识点:二阶方程的分类标准,标准型 3问顺和应用 应用:判新方程属于那种类型,并化成标准型 (三)思考与实践 勤学多练。熟练利用判别式将二阶线性常系数化成双曲型、抛物型和椭圆 型偏微分方程的标准型。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅 第三章分离变量法 (一)目的与要求 1.了解Stum-Liouville问题。 2。会用分离变量法求解齐次双曲型、抛物型和椭圆型偏微分方程的混合问 重 3.掌握边界条件齐次化的方法。 4.会用齐次化原理求解非齐次的双曲型、抛物型和椭圆型偏微分方程的混 合问题。 〖重点与难点】 1.本章的重点内容:齐次双曲型、抛物型和椭圆型偏微分方程的混合问题 与分离变量法。 2.本章的难点内容:边界条件齐次化,求解非齐次双曲型、抛物型和椭圆 型偏微分方程的混合问题。 (二)教学内容 第一节分离变量法的理论基础 4
4 3. 问题与应用 问题:为什么当初始数据在特征曲线上时,一般来说定解问题是无解的, 若有解就一定不唯一? 第二节 二阶方程的分类 1. 主要内容 两个自变量的二阶线性偏微分方程的分类,主部具有常系数的多个自变量 的二阶线性偏微分方程的分类 2. 基本概念和知识点 概念:判别式,特征二次型,双曲型、抛物型、椭圆型偏微分方程, 知识点:二阶方程的分类标准,标准型 3. 问题和应用 应用:判断方程属于那种类型,并化成标准型 (三)思考与实践 勤学多练。熟练利用判别式将二阶线性常系数化成双曲型、抛物型和椭圆 型偏微分方程的标准型。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第三章 分离变量法 (一)目的与要求 1. 了解 Sturm-Liouville 问题。 2. 会用分离变量法求解齐次双曲型、抛物型和椭圆型偏微分方程的混合问 题。 3. 掌握边界条件齐次化的方法。 4. 会用齐次化原理求解非齐次的双曲型、抛物型和椭圆型偏微分方程的混 合问题。 〖重点与难点〗 1. 本章的重点内容:齐次双曲型、抛物型和椭圆型偏微分方程的混合问题 与分离变量法。 2. 本章的难点内容:边界条件齐次化,求解非齐次双曲型、抛物型和椭圆 型偏微分方程的混合问题。 (二)教学内容 第一节 分离变量法的理论基础

1.主要内容 施图姆-刘维尔问题 2.基本概念和知识点 特征值,特征函数,完备正交基 3.问题与应用 问题:讨论分离变量法的局限性 第二节求解实例 1.主要内容 双曲型方程、抛物型方程、椭圆型方程的混合问题与分离变量法 2.基本概念和知识点 概念:下ourier正弦级数,驻波 知识点:相容性条件,驻波法,叠加原理 3.问题与应用 应用:能熟练应用分离变量法求解三类方程 (三)思考与实践 勤学多练。熟练掌握用分离变量法解双曲型、抛物型和椭圆型偏微分方程 的混合问题。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第四章双曲型方程 (一)目的与要求 l.了解如何用Duhamel原理求解Cauchy问题。 2。了解依赖区域和影响区域。 3.掌握d'Alembert公式、Poisson公式及降维法并能应用它们求解一维和高 维波动方程。 4.会应用能量不等式证明Cauchy问题解的惟一性和稳定性。 〖重点与难点】 l.本章的重点内容:Duhamel原理,应用d'Alembert公式求解一维波动方 程,应用Po1sson公式及降维法求解高维波动方程,应用能量不等式证 明Cauchy问题解的惟一性和稳定性。 2.本章的难点内容:高维波动方程的求解以及理解依赖区域和影响区域。 (二)教学内容 第一节Duhamel原理 5
5 1. 主要内容 施图姆-刘维尔问题 2. 基本概念和知识点 特征值,特征函数,完备正交基 3. 问题与应用 问题:讨论分离变量法的局限性 第二节 求解实例 1.主要内容 双曲型方程、抛物型方程、椭圆型方程的混合问题与分离变量法 2. 基本概念和知识点 概念:Fourier 正弦级数,驻波 知识点:相容性条件,驻波法,叠加原理 3. 问题与应用 应用:能熟练应用分离变量法求解三类方程 (三)思考与实践 勤学多练。熟练掌握用分离变量法解双曲型、抛物型和椭圆型偏微分方程 的混合问题。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第四章 双曲型方程 (一)目的与要求 1. 了解如何用 Duhamel 原理求解 Cauchy 问题。 2. 了解依赖区域和影响区域。 3. 掌握 d'Alembert 公式、Poisson 公式及降维法并能应用它们求解一维和高 维波动方程。 4. 会应用能量不等式证明 Cauchy 问题解的惟一性和稳定性。 〖重点与难点〗 1. 本章的重点内容:Duhamel 原理,应用 d'Alembert 公式求解一维波动方 程,应用 Poisson 公式及降维法求解高维波动方程,应用能量不等式证 明 Cauchy 问题解的惟一性和稳定性。 2. 本章的难点内容:高维波动方程的求解以及理解依赖区域和影响区域。 (二)教学内容 第一节 Duhamel 原理

1.主要内容 Cauchy问题和混合问题的齐次化原理 2.基本概念与知识点 3.问题与应用 应用:能找到适当的函数变换,将各类非齐次边界条件齐次化 第二节 一维波动方程 1.主要内容 d'Alembert公式,半直线上齐次波动方程的混合问题,非齐次波动方程的 Cauchy问颗,非齐次波动方程的混合问题 2.基本概念和知识点 概念:行波,影响区域,决定区域,依赖区域 知识点:特征线法,奇延拓,偶延拓 3.问题与应用 应用:会用特征线法求解一些变系数的双曲型方程 第三节高维波动方程 1.主要内容 二维波动方程与三维波动方程的Poisson公式,Kirchhoff公式 2.基本概念和知识点 概念:影响区域,决定区域,依赖区域 知识点:球面平均法,降维法 3.问题与应用 应用:熟练掌握降维法思想将高维方程降成低维方程 (三)思考与实践 勤学多练,熟练掌握利用d'Alembert公式求解一维波动方程。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第五章抛物型方程 (一)目的与要求 1.掌握热传导方程的求解方法。 2.了解极值原理的证明方法。 3.理解极值原理并应用其获得解的最大模估计证明解的惟一性和稳定性。 《重点与难点】 l.本章的重点内容:求解齐次、非齐次热传导方程的Cauchy问题和混合 问题
6 1. 主要内容 Cauchy 问题和混合问题的齐次化原理 2. 基本概念与知识点 3. 问题与应用 应用:能找到适当的函数变换,将各类非齐次边界条件齐次化 第二节 一维波动方程 1.主要内容 d'Alembert 公式,半直线上齐次波动方程的混合问题,非齐次波动方程的 Cauchy 问题,非齐次波动方程的混合问题 2.基本概念和知识点 概念:行波,影响区域,决定区域,依赖区域 知识点:特征线法,奇延拓,偶延拓 3.问题与应用 应用:会用特征线法求解一些变系数的双曲型方程 第三节 高维波动方程 1.主要内容 二维波动方程与三维波动方程的 Poisson 公式,Kirchhoff 公式 2.基本概念和知识点 概念:影响区域,决定区域,依赖区域 知识点:球面平均法,降维法 3.问题与应用 应用:熟练掌握降维法思想将高维方程降成低维方程 (三)思考与实践 勤学多练,熟练掌握利用 d'Alembert 公式求解一维波动方程。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第五章 抛物型方程 (一)目的与要求 1. 掌握热传导方程的求解方法。 2. 了解极值原理的证明方法。 3. 理解极值原理并应用其获得解的最大模估计证明解的惟一性和稳定性。 〖重点与难点〗 1. 本章的重点内容:求解齐次、非齐次热传导方程的 Cauchy 问题和混合 问题
2.本章的难点内容:应用极值原理获得解的最大模估计来证明解的惟 性和稳定性 (二)教学内容 第一节热传导方程定解问题的求解 1.主要内容 齐次方程和非齐次方程Cauchy问题的Poisson公式,半直线上的热传导 方程的混合问题 2.基本概念和知识点 知识点:相似变换法,自相似解,热核函数 3.问题与应用 问题:热传导方程Cauchy问题的初始条件为什么只有一个? 第二节极值原理、最大模估计、惟一性和稳定性 1.主要内容 弱极值原理,第一边值问题解的最大模估计、惟一性与稳定性, Cauchy问题解的最大模估计 2.基本概念和知识点 3.问题与应用 问题:在热传导方程解的唯一性或稳定性的定理中都加了“解是有界的” 条件,这个有界的条件是否可以去掉? (三)思考与实践 思考:试举例说明极值原理为什么对双曲型方程不成立? (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 五、各教学环节学时分配 教学环节 讲 习 小 教学时数 实验 其他教 学环节 课 课程内容 第一章 4 第二章 6 6 第三章
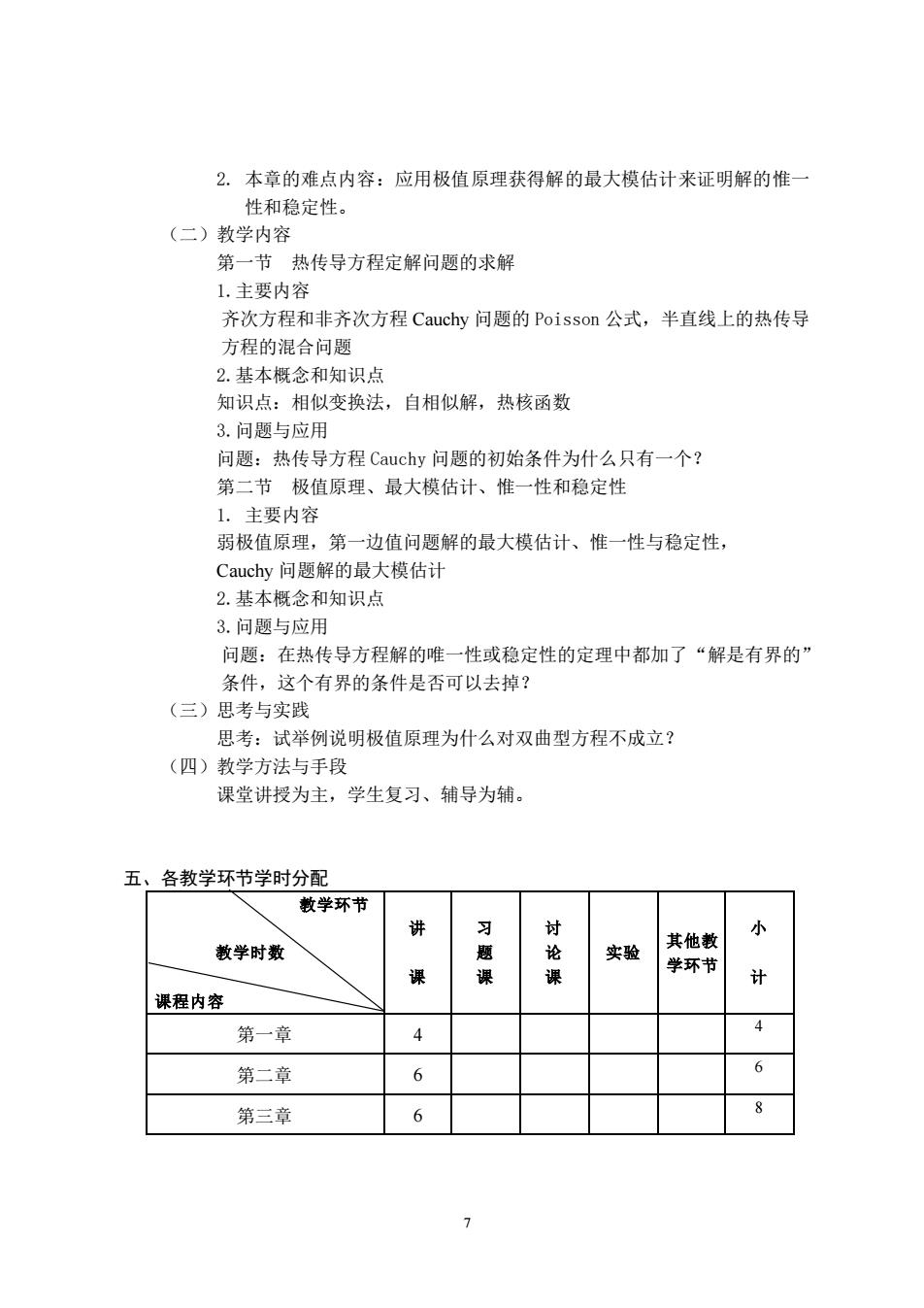
7 2. 本章的难点内容:应用极值原理获得解的最大模估计来证明解的惟一 性和稳定性。 (二)教学内容 第一节 热传导方程定解问题的求解 1.主要内容 齐次方程和非齐次方程 Cauchy 问题的 Poisson 公式,半直线上的热传导 方程的混合问题 2.基本概念和知识点 知识点:相似变换法,自相似解,热核函数 3.问题与应用 问题:热传导方程 Cauchy 问题的初始条件为什么只有一个? 第二节 极值原理、最大模估计、惟一性和稳定性 1. 主要内容 弱极值原理,第一边值问题解的最大模估计、惟一性与稳定性, Cauchy 问题解的最大模估计 2.基本概念和知识点 3.问题与应用 问题:在热传导方程解的唯一性或稳定性的定理中都加了“解是有界的” 条件,这个有界的条件是否可以去掉? (三)思考与实践 思考:试举例说明极值原理为什么对双曲型方程不成立? (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 4 4 第二章 6 6 第三章 6 8
第四章 8 第五章 6 合计 0 六、课程考核 (一)考核方式 分散考试 (二)成绩构成 平时成绩占比:40% 期末考试占比:60% (三)成绩考核标准 总成绩由课堂表现、课后作业、期末成绩三部分组成。 七、推荐教材和教学参考资源 1.朱长江,阮立志.偏微分方程简明教程。北京:高等教有出版社,2015 2.张振字,张立柱.偏微分方程上海:复旦大学出版社,2011 3.朱长江,邓引斌.偏微分方程教程.北京:科学出版社,2005 4.陈祖墀。偏微分方程(第三版).北京:高等教育出版社,2008 5。谷超章,李大潜,陈恕行等.数学物理方程(第三版),北京:高等教有出版,2012 八、其他说明 大纲修订人:彭小明 修订日期:2022年9月 大纲审定人:刘国刚 审定日期:2022年9月
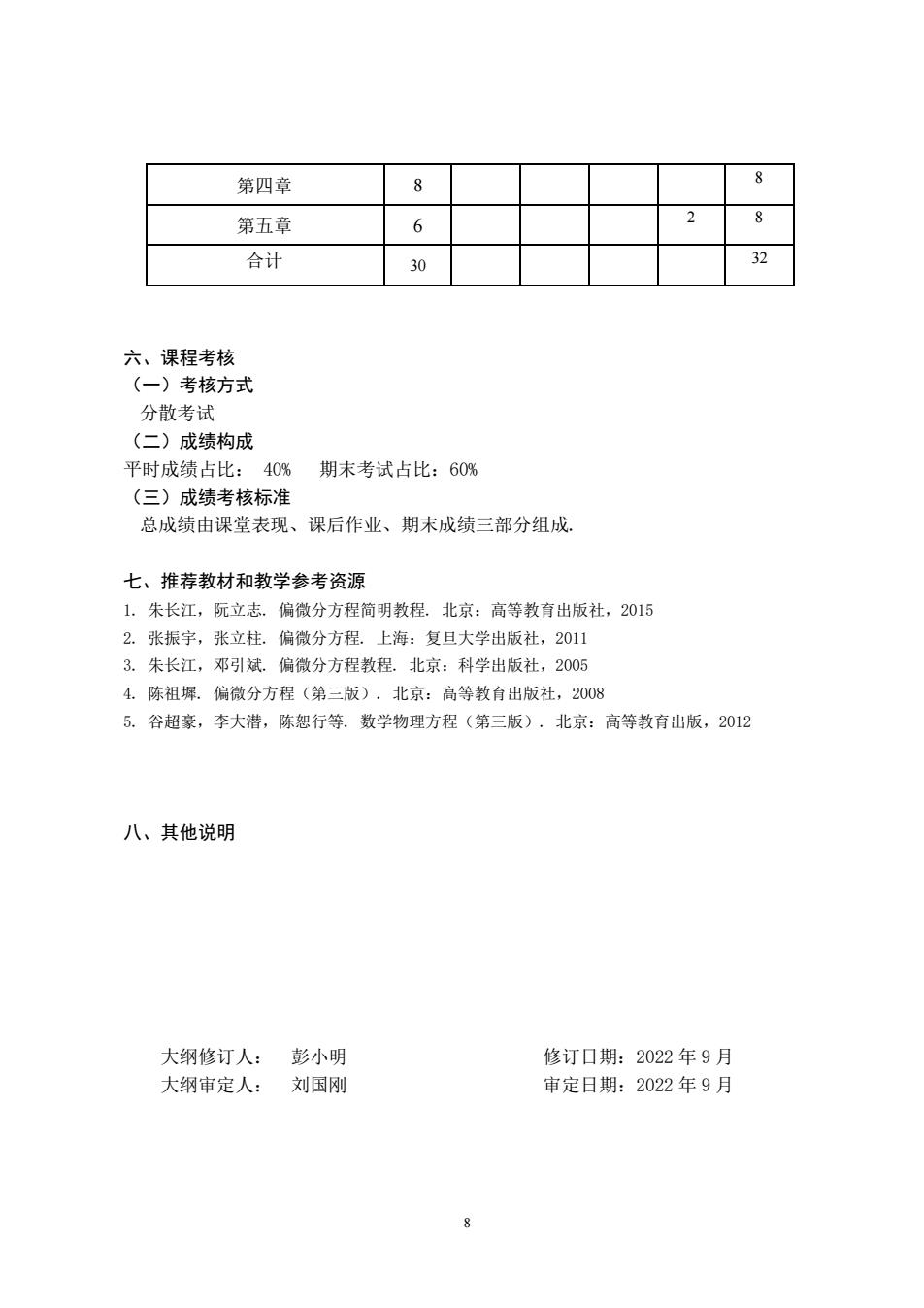
8 第四章 8 8 第五章 6 2 8 合计 30 32 六、课程考核 (一)考核方式 分散考试 (二)成绩构成 平时成绩占比: 40% 期末考试占比:60% (三)成绩考核标准 总成绩由课堂表现、课后作业、期末成绩三部分组成. 七、推荐教材和教学参考资源 1. 朱长江,阮立志. 偏微分方程简明教程. 北京:高等教育出版社,2015 2. 张振宇,张立柱. 偏微分方程. 上海:复旦大学出版社,2011 3. 朱长江,邓引斌. 偏微分方程教程. 北京:科学出版社,2005 4. 陈祖墀. 偏微分方程(第三版). 北京:高等教育出版社,2008 5. 谷超豪,李大潜,陈恕行等. 数学物理方程(第三版). 北京:高等教育出版,2012 八、其他说明 大纲修订人: 彭小明 修订日期:2022 年 9 月 大纲审定人: 刘国刚 审定日期:2022 年 9 月