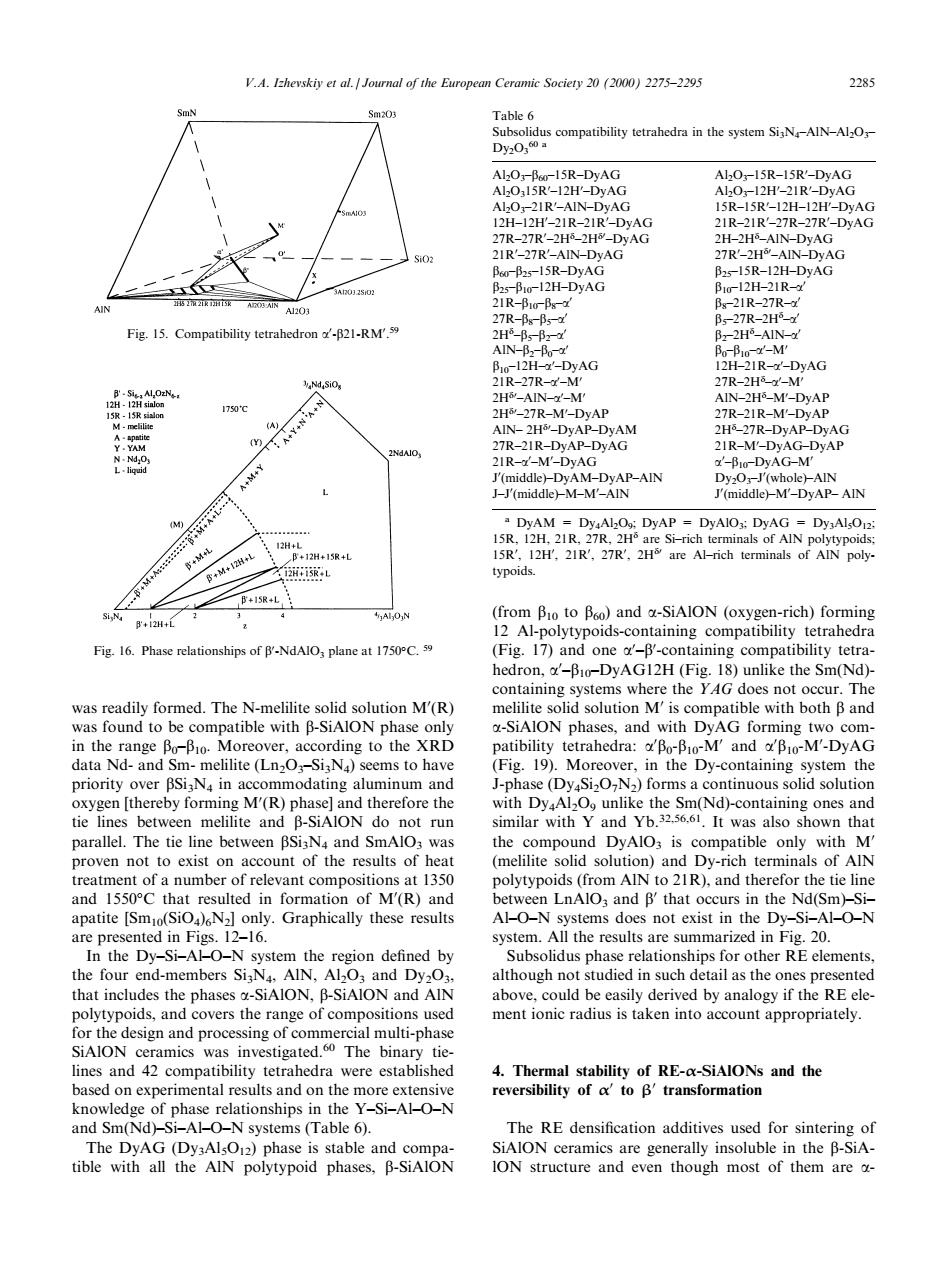
V.A.Ihevskiy et al.Journal of the European Ceramic Sociery 20(20)2275-2295 228 compatibility tetrahedra in the system SiN-AIN-AlO AlO:-Bwr-l5R-DyAG AlOr-15R-15R'-DyAG 2-2 B5- 21R-27R Fig.15.Compatibility tetrahedron -B21-RM'. 7R-2 TR-I M DAP HE M -AIN (middle)-M-DyAP-AIN .DyAM-DyALO:DyAP-DyAIO:DyAG-Dy,AlO ypoid a-SiAION ）forming Fig.16.Phase relationships of -NdAlO plane at 1750C. (Fig.17)and onecontaining compatibility tetra hedron,-Bo-DyAG12H(Fig.18)unlike the Sm(Nd) h ith DyAG or patibility tetrahedra:-MandM-DyAG n-melilite(Ln2O3-SiN)seems to have the 34 J-p Dy the sm(Nd) parallel.The tie line between BSiaN and SmAlO3 was Paennotoewioa ccount the compound DyAlO,is compatible only with M of the results of 135 (melilite on)and Dy-rich terminals of e apatite [SmiNy.Graphically these results Al-O-N systems does not exist in the Dy-Si-Al-O-N system.All the results are summarized in b、 R20 detail as above,could be easily derived by analogy if the RE ele- polytypoids,and covers the range of compositions used ment ionic radius is taken into account appropriately. esign and pro ng oacrTinti-phas lines and 42 compatibility tetrahedra were established 4.Thermal stability of RE-x-SiAlONs and the reversibility ofto B'transformation an ( ble 6) The DyAG () stable and SiAION tible with all the AIN polytypoid phases.B-SiAlON ION structure and even though most of them are was readily formed. The N-melilite solid solution M0 (R) was found to be compatible with b-SiAlON phase only in the range b0±b10. Moreover, according to the XRD data Nd- and Sm- melilite (Ln2O3±Si3N4) seems to have priority over bSi3N4 in accommodating aluminum and oxygen [thereby forming M0 (R) phase] and therefore the tie lines between melilite and b-SiAlON do not run parallel. The tie line between bSi3N4 and SmAlO3 was proven not to exist on account of the results of heat treatment of a number of relevant compositions at 1350 and 1550C that resulted in formation of M0 (R) and apatite [Sm10(SiO4)6N2] only. Graphically these results are presented in Figs. 12±16. In the Dy±Si±Al±O±N system the region de®ned by the four end-members Si3N4, AlN, Al2O3 and Dy2O3, that includes the phases a-SiAlON, b-SiAlON and AlN polytypoids, and covers the range of compositions used for the design and processing of commercial multi-phase SiAlON ceramics was investigated.60 The binary tie￾lines and 42 compatibility tetrahedra were established based on experimental results and on the more extensive knowledge of phase relationships in the Y±Si±Al±O±N and Sm(Nd)±Si±Al±O±N systems (Table 6). The DyAG (Dy3Al5O12) phase is stable and compa￾tible with all the AlN polytypoid phases, b-SiAlON (from b10 to b60) and a-SiAlON (oxygen-rich) forming 12 Al-polytypoids-containing compatibility tetrahedra (Fig. 17) and one a0 ±b0 -containing compatibility tetra￾hedron, a0 ±b10±DyAG12H (Fig. 18) unlike the Sm(Nd)- containing systems where the YAG does not occur. The melilite solid solution M0 is compatible with both b and a-SiAlON phases, and with DyAG forming two com￾patibility tetrahedra: a0 b0-b10-M0 and a0 b10-M0 -DyAG (Fig. 19). Moreover, in the Dy-containing system the J-phase (Dy4Si2O7N2) forms a continuous solid solution with Dy4Al2O9 unlike the Sm(Nd)-containing ones and similar with Y and Yb.32,56,61. It was also shown that the compound DyAlO3 is compatible only with M0 (melilite solid solution) and Dy-rich terminals of AlN polytypoids (from AlN to 21R), and therefor the tie line between LnAlO3 and b0 that occurs in the Nd(Sm)±Si± Al±O±N systems does not exist in the Dy±Si±Al±O±N system. All the results are summarized in Fig. 20. Subsolidus phase relationships for other RE elements, although not studied in such detail as the ones presented above, could be easily derived by analogy if the RE ele￾ment ionic radius is taken into account appropriately. 4. Thermal stability of RE--SiAlONs and the reversibility of 0 to 0 transformation The RE densi®cation additives used for sintering of SiAlON ceramics are generally insoluble in the b-SiA￾lON structure and even though most of them are a￾Fig. 15. Compatibility tetrahedron a0 -b21-RM0 . 59 Fig. 16. Phase relationships of b0 -NdAlO3 plane at 1750C. 59 Table 6 Subsolidus compatibility tetrahedra in the system Si3N4±AlN±Al2O3± Dy2O3 60 a Al2O3±b60±15R±DyAG Al2O3±15R±15R0 ±DyAG Al2O315R0 ±12H0 ±DyAG Al2O3±12H0 ±21R0 ±DyAG Al2O3±21R0 ±AlN±DyAG 15R±15R0 ±12H±12H0 ±DyAG 12H±12H0 ±21R±21R0 ±DyAG 21R±21R0 ±27R±27R0 ±DyAG 27R±27R0 ±2Hd ±2Hd0 ±DyAG 2H±2Hd ±AlN±DyAG 21R0 ±27R0 ±AlN±DyAG 27R0 ±2Hd0 ±AlN±DyAG b60±b25±15R±DyAG b25±15R±12H±DyAG b25±b10±12H±DyAG b10±12H±21R±a0 21R±b10±b8±a0 b8±21R±27R±a0 27R±b8±b5±a0 b5±27R±2Hd ±a0 2Hd ±b5±b2±a0 b2±2Hd ±AlN±a0 AlN±b2±b0±a0 b0±b10±a0 ±M0 b10±12H±a0 ±DyAG 12H±21R±a0 ±DyAG 21R±27R±a0 ±M0 27R±2Hd ±a0 ±M0 2Hd0 ±AlN±a0 ±M0 AlN±2Hd ±M0 ±DyAP 2Hd0 ±27R±M0 ±DyAP 27R±21R±M0 ±DyAP AlN± 2Hd0 ±DyAP±DyAM 2Hd ±27R±DyAP±DyAG 27R±21R±DyAP±DyAG 21R±M0 ±DyAG±DyAP 21R±a0 ±M0 ±DyAG a0 ±b10±DyAG±M0 J0 (middle)±DyAM±DyAP±AlN Dy2O3±J0 (whole)±AlN J±J0 (middle)±M±M0 ±AlN J0 (middle)±M0 ±DyAP± AlN a DyAM = Dy4Al2O9; DyAP = DyAlO3; DyAG = Dy3Al5O12; 15R, 12H, 21R, 27R, 2Hd are Si±rich terminals of AlN polytypoids; 15R0 , 12H0 , 21R0 , 27R0 , 2Hd0 are Al±rich terminals of AlN poly￾typoids. V.A. Izhevskiy et al. / Journal of the European Ceramic Society 20 (2000) 2275±2295 2285