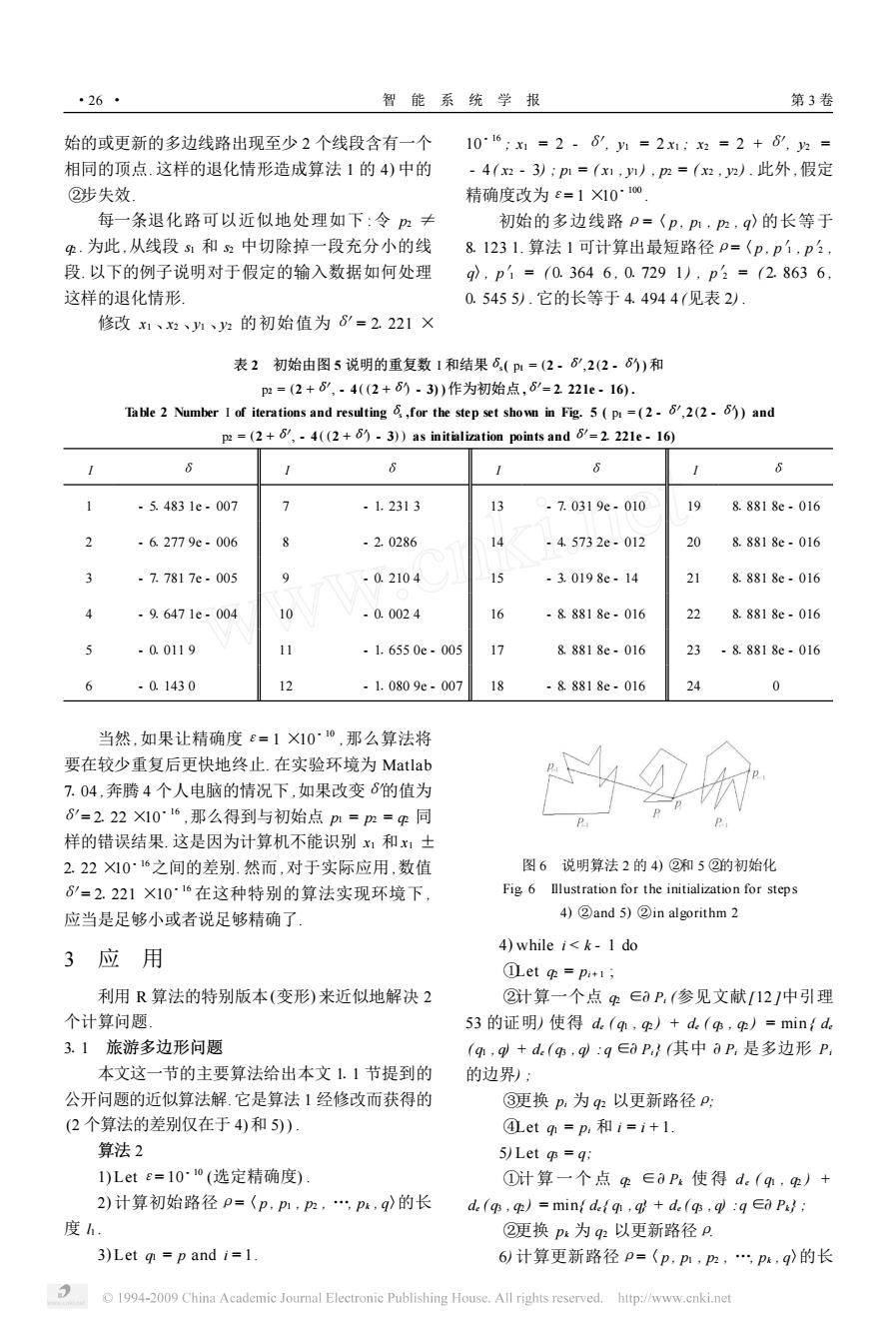
·26· 智能系统学报 第3卷 始的或更新的多边线路出现至少2个线段含有一个 106;x1=2-6,M=2x1;x2=2+8,2= 相同的顶点.这样的退化情形造成算法1的4)中的 -4(x2-3);pm1=(x1,n),p=(x2,2).此外，假定 ②步失效」 精确度改为e=1X101oo」 每一条退化路可以近似地处理如下：令历≠ 初始的多边线路p=〈p,p,m,g〉的长等于 .为此，从线段和2中切除掉一段充分小的线 8.1231.算法1可计算出最短路径p=〈p,p1,p?, 段.以下的例子说明对于假定的输入数据如何处理 q,p1=(0.3646,0.7291),p2=(2.8636, 这样的退化情形 0.5455).它的长等于4.4944（见表2）. 修改x1、2、h、2的初始值为6=2.221× 表2初始由图5说明的重复数1和结果6，(p=(2.6',2(2·6)和 2=(2+6”,-4(2+6)-3)作为初始点，6-2221e-16. Table 2 Number I of iterations and resulting ,for the step set shown in Fig.5(p=(2-6,2(2)and p2 =(2+6,-4((2+6)-3))as initialization points and 6/=2 22le-16) 6 6 -5.4831e-007 7 -1.2313 13 .7.0319e-010 g 8.8818e-016 2 -6.2779e-006 8 -2.0286 14 -45732e.012 20 8.8818e-016 3 -7.7817e-005 9 -0.2104 -3.0198e-14 21 8.8818e-016 4 -9.6471e.004 10 -0.0024 16 -8.8818e-016 22 8.8818e-016 -0.0119 11 -1.6550e-005 8.8818e-016 2 -8.8818e-016 -0.1430 12 -1.0809e-007 18 -8.8818e-016 24 0 当然，如果让精确度￡=1X10~°，那么算法将 要在较少重复后更快地终止.在实验环境为Matlab 7.04,奔腾4个人电脑的情况下，如果改变6的值为 8=2.22X1016,那么得到与初始点pm=pm=p同 样的错误结果.这是因为计算机不能识别x1和x1士 2.221016之间的差别.然而，对于实际应用，数值 图6说明算法2的4)②和5②的初始化 8=2.221×10~16在这种特别的算法实现环境下， Fig 6 lllustration for the initialization for steps 应当是足够小或者说足够精确了. 4)②and5)②in algorithm2 4)while i<k-1 do 3应用 ①etp=pi+1； 利用R算法的特别版本（变形）来近似地解决2 ②计算一个点∈0P(参见文献121中引理 个计算问题 53的证明)使得d.(q,)+d.(,)=min{de 3.1旅游多边形问题 (m,g+d.(,q:q∈P}(其中aP,是多边形P 本文这一节的主要算法给出本文1.1节提到的 的边界)： 公开问题的近似算法解.它是算法1经修改而获得的 ③更换p,为q2以更新路径P: (2个算法的差别仅在于4)和5) ④etqm=p,和i=i+1. 算法2 5)Let gs=q: 1)Letc=10~io(选定精确度) ①计算一个点∈aP使得d.(,)+ 2)计算初始路径p=〈p,pm,pm,,p,q〉的长 de(s q)=mint de(n,q+d.(s.q :qep 度h. ②更换p:为q以更新路径P. 3)Let g=p and i=1. 6)计算更新路径p=〈p,pP,p,p,q的长 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net始的或更新的多边线路出现至少 2 个线段含有一个 相同的顶点. 这样的退化情形造成算法 1 的 4) 中的 ②步失效. 每一条退化路可以近似地处理如下 :令 p2 ≠ q2 . 为此 ,从线段 s1 和 s2 中切除掉一段充分小的线 段. 以下的例子说明对于假定的输入数据如何处理 这样的退化情形. 修改 x1 、x2 、y1 、y2 的初始值为δ′= 21221 × 10 - 16 ; x1 = 2 - δ′, y1 = 2 x1 ; x2 = 2 + δ′, y2 = - 4 ( x2 - 3) ; p1 = ( x1 , y1 ) , p2 = ( x2 , y2 ) . 此外 ,假定 精确度改为ε= 1 ×10 - 100 . 初始的多边线路ρ=〈 p , p1 , p2 , q〉的长等于 81123 1. 算法 1 可计算出最短路径ρ=〈p , p′1 , p′2 , q〉, p′1 = ( 01364 6 , 01729 1 ) , p′2 = ( 21863 6 , 01545 5) . 它的长等于 41494 4 (见表 2) . 表 2 初始由图 5 说明的重复数 I 和结果δs( p1 = (2 - δ′,2 (2 - δ′) ) 和 p2 = (2 +δ′, - 4 ( (2 +δ′) - 3) )作为初始点 ,δ′= 21221e - 16) . Table 2 Number I of iterations and resultingδs ,for the step set shown in Fig. 5 ( p1 = ( 2 - δ′,2 (2 - δ′) ) and p2 = (2 +δ′, - 4 ( (2 +δ′) - 3) ) as initialization points andδ′= 21221e - 16) I δ I δ I δ I δ 1 - 51483 1e - 007 7 - 11231 3 13 - 71031 9e - 010 19 81881 8e - 016 2 - 61277 9e - 006 8 - 210286 14 - 41573 2e - 012 20 81881 8e - 016 3 - 71781 7e - 005 9 - 01210 4 15 - 31019 8e - 14 21 81881 8e - 016 4 - 91647 1e - 004 10 - 01002 4 16 - 81881 8e - 016 22 81881 8e - 016 5 - 01011 9 11 - 11655 0e - 005 17 81881 8e - 016 23 - 81881 8e - 016 6 - 01143 0 12 - 11080 9e - 007 18 - 81881 8e - 016 24 0 当然 ,如果让精确度ε= 1 ×10 - 10 ,那么算法将 要在较少重复后更快地终止. 在实验环境为 Matlab 7104 ,奔腾 4 个人电脑的情况下 ,如果改变δ′的值为 δ′= 2122 ×10 - 16 ,那么得到与初始点 p1 = p2 = q2 同 样的错误结果. 这是因为计算机不能识别 x1 和 x1 ± 2122 ×10 - 16之间的差别. 然而 ,对于实际应用 ,数值 δ′= 21221 ×10 - 16 在这种特别的算法实现环境下 , 应当是足够小或者说足够精确了. 3 应 用 利用 R 算法的特别版本(变形) 来近似地解决 2 个计算问题. 311 旅游多边形问题 本文这一节的主要算法给出本文 111 节提到的 公开问题的近似算法解.它是算法 1 经修改而获得的 (2 个算法的差别仅在于 4)和 5)) . 算法 2 1) Letε= 10 - 10 (选定精确度) . 2) 计算初始路径ρ=〈p , p1 , p2 , …, pk , q〉的长 度 l1 . 3) Let q1 = p and i = 1. 图 6 说明算法 2 的 4) ②和 5 ②的初始化 Fig16 Illustration for the initialization for step s 4) ②and 5) ②in algorithm 2 4) while i < k - 1 do ①Let q2 = pi + 1 ; ②计算一个点 q2 ∈9 Pi (参见文献[12 ]中引理 53 的证明) 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min { de ( q1 , q) + de ( q3 , q) : q ∈9 Pi} (其中 9 Pi 是多边形 Pi 的边界) ; ③更换 pi 为 q2 以更新路径ρ; ④Let q1 = pi 和 i = i + 1. 5) Let q3 = q; ①计算一个点 q2 ∈9 Pk 使得 de ( q1 , q2 ) + de ( q3 , q2 ) = min{ de { q1 , q} + de ( q3 , q) :q ∈9 Pk } ; ②更换 pk 为 q2 以更新路径ρ. 6) 计算更新路径ρ=〈p , p1 , p2 , …, pk , q〉的长 ·26 · 智 能 系 统 学 报 第 3 卷