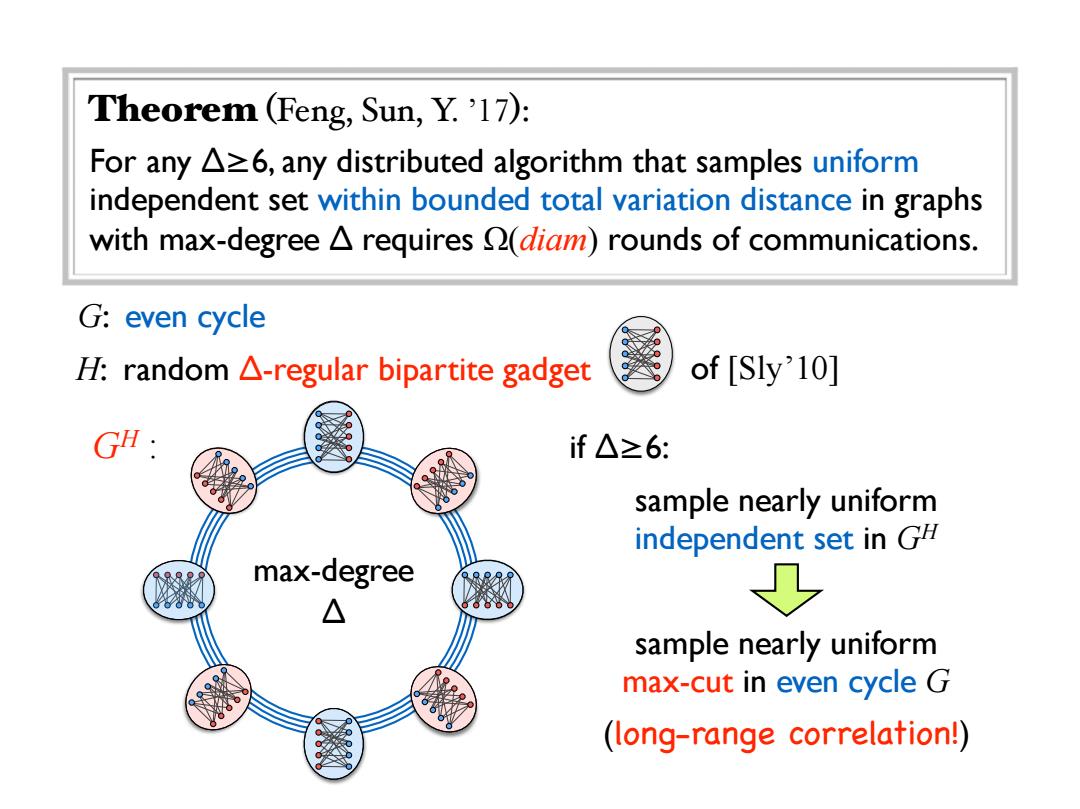
Theorem (Feng,Sun,Y.'17): For any△≥6，any distributed algorithm that samples uniform independent set within bounded total variation distance in graphs with max-degree A requires (diam)rounds of communications. G: even cycle H:random A-regular bipartite gadget of [Sly'10] GH: if△≥6： sample nearly uniform independent set in G# max-degree △ ↓ sample nearly uniform max-cut in even cycle G (long-range correlation!)Theorem (Feng, Sun, Y. ’17): For any ∆≥6, any distributed algorithm that samples uniform independent set within bounded total variation distance in graphs with max-degree ∆ requires Ω(diam) rounds of communications. G: even cycle H: random ∆-regular bipartite gadget GH : if ∆≥6: max-degree ∆ sample nearly uniform independent set in GH sample nearly uniform max-cut in even cycle G (long-range correlation!) of [Sly’10]