正在加载图片...
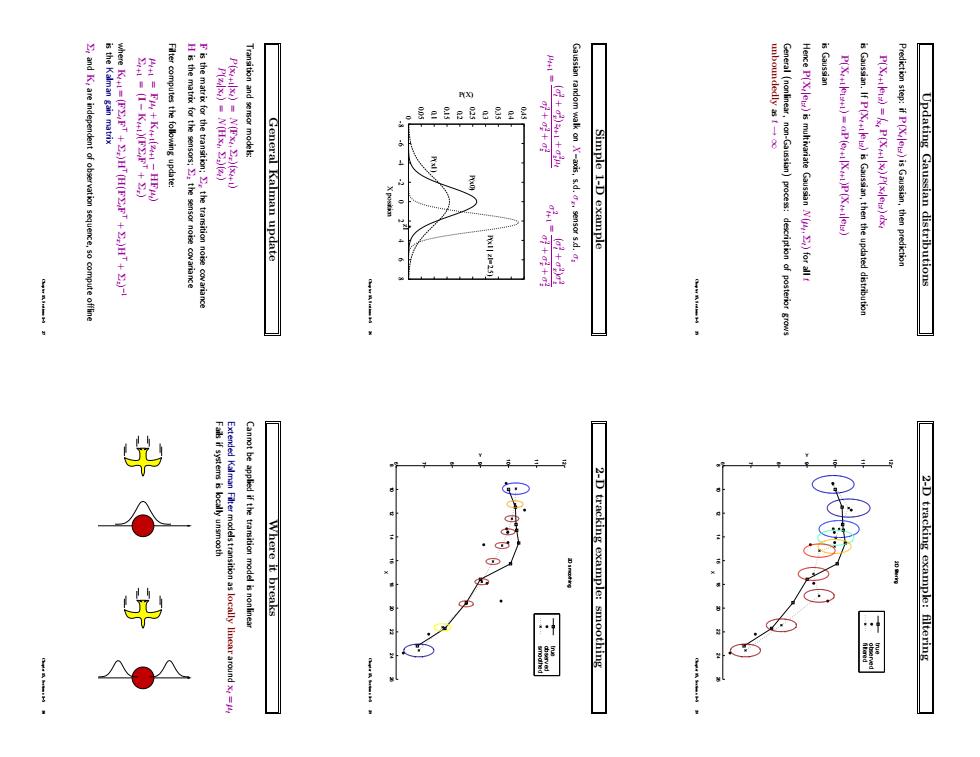
is Gaussian sequence,so compute offlin General Kalman update +8+元 Gaussian random walk ons.d.se Simple I-D example Here P(X)s multivariate Gaussian N for al t Prediction step:if P()is Gaussian,then RA113-25 Updating Gaussian distributions Where it breaks 2-D tracking example:smoothing 2-D tracking example:filteringUpdating Gaussian distributions Prediction step: if P(Xt |e1:t) is Gaussian, then prediction P(Xt+1|e1:t) = Z xt P(Xt+1|xt)P(xt |e1:t) dxt is Gaussian. If P(Xt+1|e1:t) is Gaussian, then the updated distribution P(Xt+1|e1:t+1) = αP(et+1|Xt+1)P(Xt+1|e1:t) is Gaussian Hence P(Xt |e1:t) is multivariate Gaussian N(µt , Σt) for all t General (nonlinear, non-Gaussian) process: description of posterior grows unboundedly as t → ∞ Chapter 15, Sections 1–5 25 Simple 1-D example Gaussian random walk on X–axis, s.d. σx, sensor s.d. σz µt+1 = (σt 2 + σx 2 )zt+1 + σz 2µt σt 2 + σx 2 + σz 2 σt+1 2 = (σt 2 + σx 2 )σz 2 σt 2 + σx 2 + σz 2 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 -8 -6 -4 -2 0 2 4 6 8 P(X) X position P(x0) P(x1) P(x1 | z1=2.5) z1 * Chapter 15, Sections 1–5 26 General Kalman update Transition and sensor models: P(xt+1|xt) = N(Fxt , Σx)(xt+1) P(zt |xt) = N(Hxt , Σz)(zt) F is the matrix for the transition; Σx the transition noise covariance H is the matrix for the sensors; Σz the sensor noise covariance Filter computes the following update: µt+1 = Fµt + Kt+1(zt+1 − HFµt ) Σt+1 = (I − Kt+1)(FΣtF > + Σx) where Kt+1 = (FΣtF > + Σx)H> (H(FΣtF > + Σx)H> + Σz) −1 is the Kalman gain matrix Σt and Kt are independent of observation sequence, so compute offline Chapter 15, Sections 1–5 27 2-D tracking example: filtering 8 10 12 14 16 18 20 22 24 26 6 7 8 9 10 11 12 X Y 2D filtering filtered observed true Chapter 15, Sections 1–5 28 2-D tracking example: smoothing 8 10 12 14 16 18 20 22 24 26 6 7 8 9 10 11 12 X Y 2D smoothing smoothed observed true Chapter 15, Sections 1–5 29 Where it breaks Cannot be applied if the transition model is nonlinear Extended Kalman Filter models transition as locally linear around xt = µt Fails if systems is locally unsmooth Chapter 15, Sections 1–5 30