
Dynamic Bayesian network Hidden Markov model Time and uncertainty Time and uncertainty Kalman filters (a brief mention Outlin CHAPTER 15,SECTIONS 1- TEMPORAL PROBABILITY MODE Fr-arder Inference tasks Sensor Markov assumption:P(EX E-1)-P(EX) asumption:X depends on bounded subset of X Markov processes (Markoy chains) rrF
Temporal probability models Chapter 15, Sections 1–5 Chapter 15, Sections 1–5 1 Outline ♦ Time and uncertainty ♦ Inference: filtering, prediction, smoothing ♦ Hidden Markov models ♦ Kalman filters (a brief mention) ♦ Dynamic Bayesian networks ♦ Particle filtering Chapter 15, Sections 1–5 2 Time and uncertainty The world changes; we need to track and predict it Diabetes management vs vehicle diagnosis Basic idea: copy state and evidence variables for each time step Xt = set of unobservable state variables at time t e.g., BloodSugart , StomachContentst , etc. Et = set of observable evidence variables at time t e.g., MeasuredBloodSugart , PulseRatet , FoodEatent This assumes discrete time; step size depends on problem Notation: Xa:b = Xa, Xa+1, . . . , Xb−1, Xb Chapter 15, Sections 1–5 3 Markov processes (Markov chains) Construct a Bayes net from these variables: parents? Markov assumption: Xt depends on bounded subset of X0:t−1 First-order Markov process: P(Xt |X0:t−1) = P(Xt |Xt−1) Second-order Markov process: P(Xt |X0:t−1) = P(Xt |Xt−2, Xt−1) X t −1 X t X t −2 X t +1 X t +2 X t −1 X t X t −2 X t +1 X t +2 Senso Second−order First−order r Markov assumption: P(Et |X0:t , E0:t−1) = P(Et |Xt) Stationary process: transition model P(Xt |Xt−1) and sensor model P(Et |Xt) fixed for all t Chapter 15, Sections 1–5 4 Example t Rain t Umbrella Raint −1 Umbrellat −1 Raint +1 Umbrellat +1 Rt −1 t P(R ) 0.3 f 0.7 t t R t P(U ) 0.9 t 0.2 f First-order Markov assumption not exactly true in real world! Possible fixes: 1. Increase order of Markov process 2. Augment state, e.g., add Tempt , Pressuret Example: robot motion. Augment position and velocity with Batteryt Chapter 15, Sections 1–5 5 Inference tasks Filtering: P(Xt |e1:t) belief state—input to the decision process of a rational agent Prediction: P(Xt+k|e1:t) for k > 0 evaluation of possible action sequences; like filtering without the evidence Smoothing: P(Xk|e1:t) for 0 ≤ k < t better estimate of past states, essential for learning Most likely explanation: arg maxx1:t P(x1:t |e1:t) speech recognition, decoding with a noisy channel Chapter 15, Sections 1–5 6
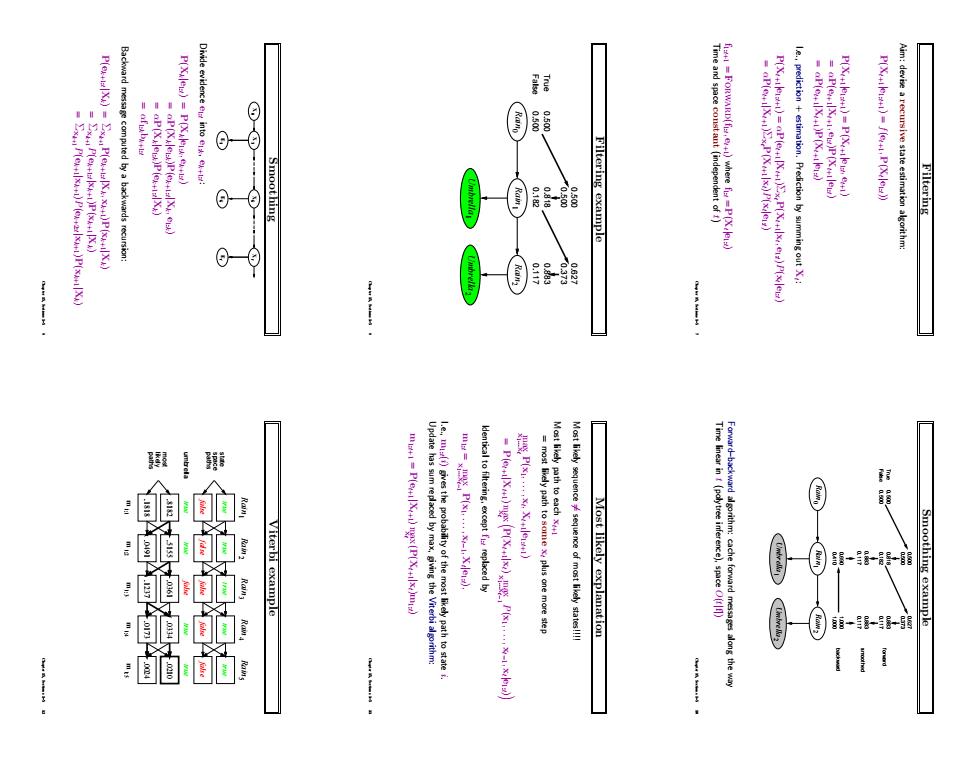
P(Xxle)P(Xe P()P(+X) Divide evidence e intoe Smoothing T 5) Aim:devise a recursive state estimation algorithm Filtering iterbi examplo kenticaltoflteringexceptreplaced by Most likely explanation Smoothing example 的
Filtering Aim: devise a recursive state estimation algorithm: P(Xt+1|e1:t+1) = f(et+1, P(Xt |e1:t)) P(Xt+1|e1:t+1) = P(Xt+1|e1:t , et+1) = αP(et+1|Xt+1, e1:t)P(Xt+1|e1:t) = αP(et+1|Xt+1)P(Xt+1|e1:t) I.e., prediction + estimation. Prediction by summing out Xt : P(Xt+1|e1:t+1) = αP(et+1|Xt+1)ΣxtP(Xt+1|xt , e1:t)P(xt |e1:t) = αP(et+1|Xt+1)ΣxtP(Xt+1|xt)P(xt |e1:t) f1:t+1 = Forward(f1:t , et+1) where f1:t = P(Xt |e1:t) Time and space constant (independent of t) Chapter 15, Sections 1–5 7 Filtering example Rain1 Umbrella1 Rain2 Umbrella2 Rain0 0.182 0.818 0.117 0.883 0.373 0.627 False True 0.500 0.500 0.500 0.500 Chapter 15, Sections 1–5 8 Smoothing X 0 X 1 1 E Ek t E t X X k Divide evidence e1:t into e1:k, ek+1:t : P(Xk|e1:t) = P(Xk|e1:k, ek+1:t) = αP(Xk|e1:k)P(ek+1:t |Xk, e1:k) = αP(Xk|e1:k)P(ek+1:t |Xk) = αf1:kbk+1:t Backward message computed by a backwards recursion: P(ek+1:t |Xk) = Σxk+1P(ek+1:t |Xk, xk+1)P(xk+1|Xk) = Σxk+1P(ek+1:t |xk+1)P(xk+1|Xk) = Σxk+1P(ek+1|xk+1)P(ek+2:t |xk+1)P(xk+1|Xk) Chapter 15, Sections 1–5 9 Smoothing example Rain1 Umbrella1 Rain2 Umbrella2 Rain0 False True 0.182 0.818 0.117 0.883 0.373 0.627 0.500 0.500 0.500 0.500 1.000 1.000 0.410 0.690 0.117 0.883 backward smoothed forward 0.117 0.883 Forward–backward algorithm: cache forward messages along the way Time linear in t (polytree inference), space O(t|f|) Chapter 15, Sections 1–5 10 Most likely explanation Most likely sequence 6= sequence of most likely states!!!! Most likely path to each xt+1 = most likely path to some xt plus one more step x max 1...xt P(x1, . . . , xt , Xt+1|e1:t+1) = P(et+1|Xt+1) max xt P(Xt+1|xt) max x1...xt−1 P(x1, . . . , xt−1, xt |e1:t) Identical to filtering, except f1:t replaced by m1:t = max x1...xt−1 P(x1, . . . , xt−1, Xt |e1:t), I.e., m1:t(i) gives the probability of the most likely path to state i. Update has sum replaced by max, giving the Viterbi algorithm: m1:t+1 = P(et+1|Xt+1) max xt (P(Xt+1|xt)m1:t) Chapter 15, Sections 1–5 11 Viterbi example Rain1 Rain2 Rain3 Rain4 Rain5 false true false true false true false true false true .8182 .5155 .0361 .0334 .0210 .1818 .0491 .1237 .0173 .0024 m 1:1 m 1:5 m 1:4 m 1:3 m 1:2 paths likely most umbrella paths space state true true true false true Chapter 15, Sections 1–5 12

82333 Country dance algorithm Country dance algorithm rd-backward arithm need time()and space ( Forward and backward mesa cdumn vectors diagonal elementsP Hidden Markoy models 0 会 ① Country dance algorithm Country dance algorithm Algorithm:rward pass computes pass does f b Country dance algorithm
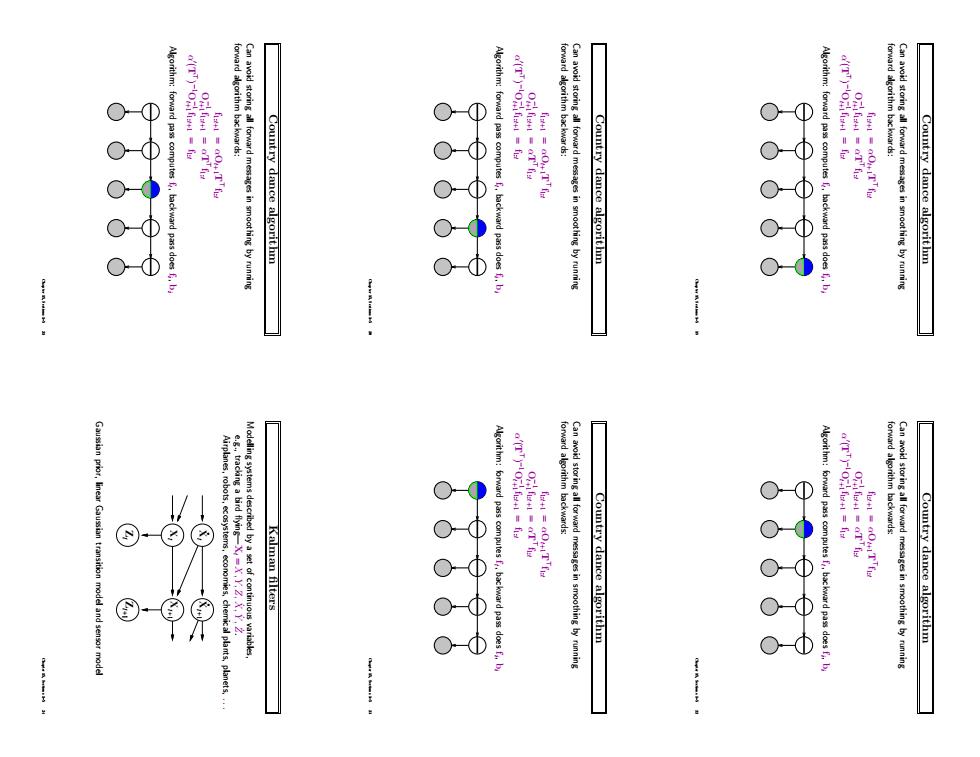
Hidden Markov models Xt is a single, discrete variable (usually Et is too) Domain of Xt is {1, . . . , S} Transition matrix Tij = P(Xt = j|Xt−1 = i), e.g., 0.7 0.3 0.3 0.7 Sensor matrix Ot for each time step, diagonal elements P(et |Xt = i) e.g., with U1 = true, O1 = 0.9 0 0 0.2 Forward and backward messages as column vectors: f1:t+1 = αOt+1T > f1:t bk+1:t = TOk+1bk+2:t Forward-backward algorithm needs time O(S 2 t) and space O(St) Chapter 15, Sections 1–5 13 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 14 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 15 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 16 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 17 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 18
3533 0 ① Country dance algorithm Country dance algorithm Algorithm:forward pass computes,backward pass does b Country dance algorithm linear Gau (TT)O=fia model and sen Kalman filters m1 Country dance algorithm Country dance algorithm
Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 19 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 20 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 21 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 22 Country dance algorithm Can avoid storing all forward messages in smoothing by running forward algorithm backwards: f1:t+1 = αOt+1T > f1:t O−1 t+1 f1:t+1 = αT > f1:t α 0 (T > ) − O1 −1 t+1 f1:t+1 = f1:t Algorithm: forward pass computes ft , backward pass does fi , bi Chapter 15, Sections 1–5 23 Kalman filters Modelling systems described by a set of continuous variables, e.g., tracking a bird flying—Xt = X, Y, Z, X˙ , Y˙ , Z˙ . Airplanes, robots, ecosystems, economies, chemical plants, planets, . . . t Z t+1 Z t X t+1 X t X t+1 X Gaussian prior, linear Gaussian transition model and sensor model Chapter 15, Sections 1–5 24
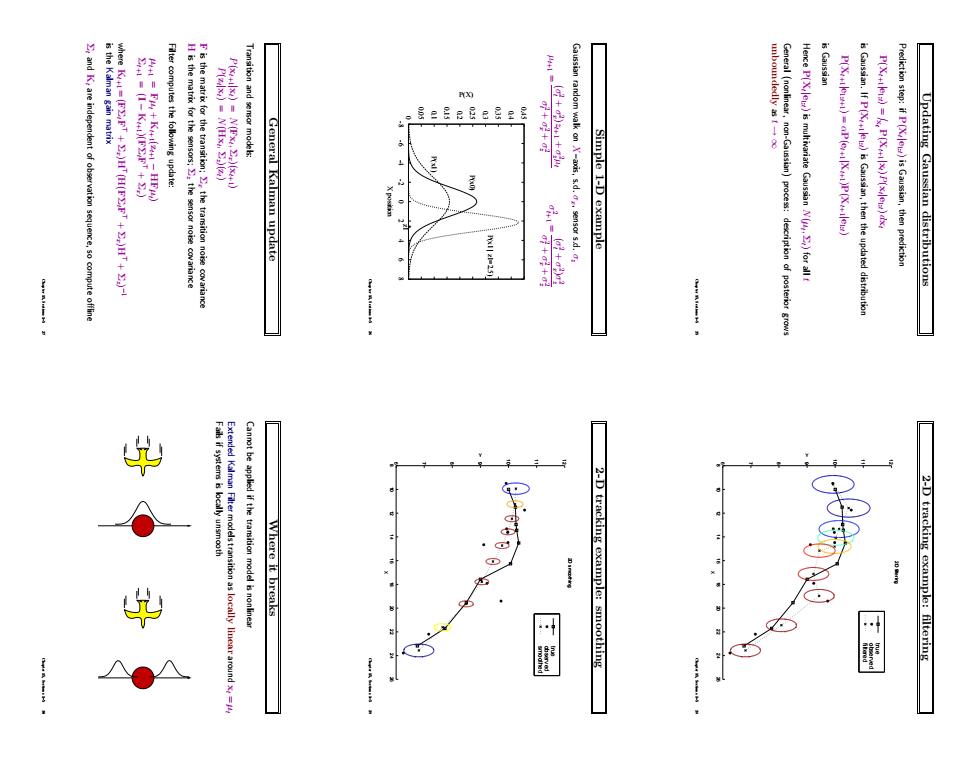
is Gaussian sequence,so compute offlin General Kalman update +8+元 Gaussian random walk ons.d.se Simple I-D example Here P(X)s multivariate Gaussian N for al t Prediction step:if P()is Gaussian,then RA113-25 Updating Gaussian distributions Where it breaks 2-D tracking example:smoothing 2-D tracking example:filtering
Updating Gaussian distributions Prediction step: if P(Xt |e1:t) is Gaussian, then prediction P(Xt+1|e1:t) = Z xt P(Xt+1|xt)P(xt |e1:t) dxt is Gaussian. If P(Xt+1|e1:t) is Gaussian, then the updated distribution P(Xt+1|e1:t+1) = αP(et+1|Xt+1)P(Xt+1|e1:t) is Gaussian Hence P(Xt |e1:t) is multivariate Gaussian N(µt , Σt) for all t General (nonlinear, non-Gaussian) process: description of posterior grows unboundedly as t → ∞ Chapter 15, Sections 1–5 25 Simple 1-D example Gaussian random walk on X–axis, s.d. σx, sensor s.d. σz µt+1 = (σt 2 + σx 2 )zt+1 + σz 2µt σt 2 + σx 2 + σz 2 σt+1 2 = (σt 2 + σx 2 )σz 2 σt 2 + σx 2 + σz 2 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 -8 -6 -4 -2 0 2 4 6 8 P(X) X position P(x0) P(x1) P(x1 | z1=2.5) z1 * Chapter 15, Sections 1–5 26 General Kalman update Transition and sensor models: P(xt+1|xt) = N(Fxt , Σx)(xt+1) P(zt |xt) = N(Hxt , Σz)(zt) F is the matrix for the transition; Σx the transition noise covariance H is the matrix for the sensors; Σz the sensor noise covariance Filter computes the following update: µt+1 = Fµt + Kt+1(zt+1 − HFµt ) Σt+1 = (I − Kt+1)(FΣtF > + Σx) where Kt+1 = (FΣtF > + Σx)H> (H(FΣtF > + Σx)H> + Σz) −1 is the Kalman gain matrix Σt and Kt are independent of observation sequence, so compute offline Chapter 15, Sections 1–5 27 2-D tracking example: filtering 8 10 12 14 16 18 20 22 24 26 6 7 8 9 10 11 12 X Y 2D filtering filtered observed true Chapter 15, Sections 1–5 28 2-D tracking example: smoothing 8 10 12 14 16 18 20 22 24 26 6 7 8 9 10 11 12 X Y 2D smoothing smoothed observed true Chapter 15, Sections 1–5 29 Where it breaks Cannot be applied if the transition model is nonlinear Extended Kalman Filter models transition as locally linear around xt = µt Fails if systems is locally unsmooth Chapter 15, Sections 1–5 30
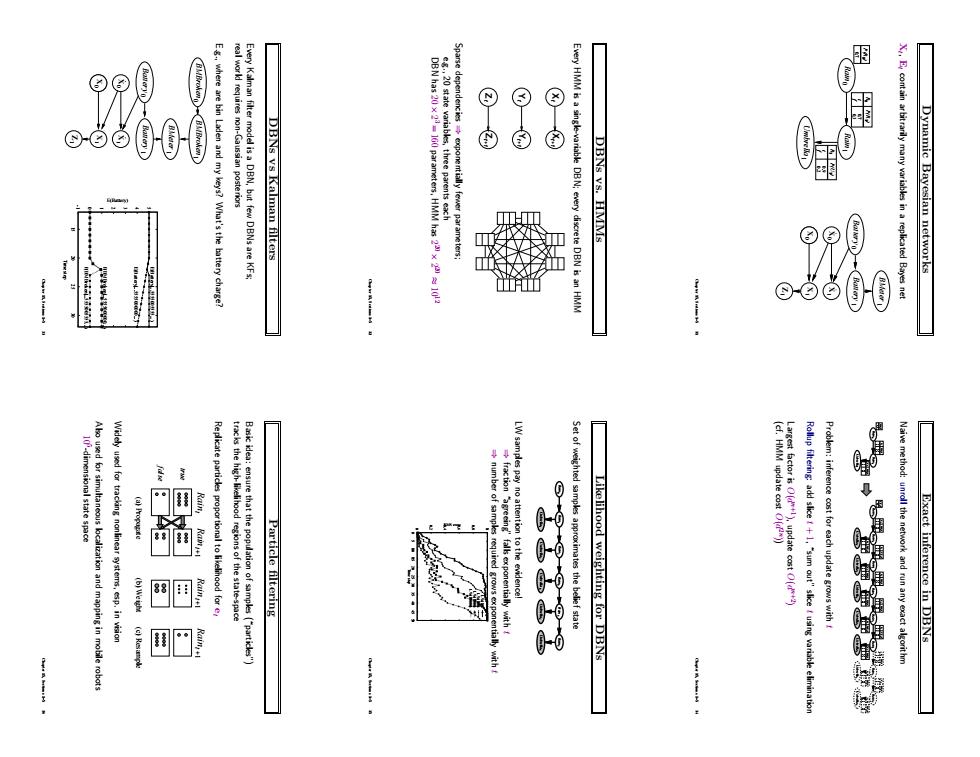
are bin Lade ⊙ DBNs vs Kalman filters Every HMM is a single-variable en and my keys?What's the battery charge? 金:DBNBmHHN DE DBNs vs.HMMs Dynamic Bayesian networks Widely used for tracking nonlinear systems,sp.in vision 网阳雕 Particle filtering to the evidencel of weighted samples approximates the belief state Likelihood weighting for DBNs Problem:inference ost for each update grows with Naive method:the network and runany exact algorithm Exact inference in DBNs
Dynamic Bayesian networks Xt , Et contain arbitrarily many variables in a replicated Bayes net 0.3 f 0.7 t 0.9 t 0.2 f Rain0 Rain1 Umbrella1 P(U ) 1 R1 P(R ) 1 R0 0.7 P(R )0 Z1 X1 X1 Xt 0 X 0 1 Battery Battery 0 1 BMeter Chapter 15, Sections 1–5 31 DBNs vs. HMMs Every HMM is a single-variable DBN; every discrete DBN is an HMM Xt Xt+1 t Y t+1 Y t Z t+1 Z Sparse dependencies ⇒ exponentially fewer parameters; e.g., 20 state variables, three parents each DBN has 20 × 2 3 = 160 parameters, HMM has 2 20 × 2 20 ≈ 10 12 Chapter 15, Sections 1–5 32 DBNs vs Kalman filters Every Kalman filter model is a DBN, but few DBNs are KFs; real world requires non-Gaussian posteriors E.g., where are bin Laden and my keys? What’s the battery charge? Z1 X1 X1 Xt 0 X 0 1 Battery Battery 0 1 BMeter 0 BMBroken 1 BMBroken -1 0 1 2 3 4 5 15 20 25 30 E(Battery) Time step P(BMBroken|...5555005555...) P(BMBroken|...5555000000...) E(Battery|...5555000000...) E(Battery|...5555005555...) Chapter 15, Sections 1–5 33 Exact inference in DBNs Naive method: unroll the network and run any exact algorithm 0.3 f 0.7 t 0.9 t 0.2 f Rain1 Umbrella1 P(U ) 1 R1 P(R ) 1 R0 Rain0 0.7 P(R )0 0.3 f 0.7 t 0.9 t 0.2 f Rain1 Umbrella1 P(U ) 1 R1 P(R ) 1 R0 0.3 f 0.7 t 0.9 t 0.2 f P(U ) 1 R1 P(R ) 1 R0 0.3 f 0.7 t 0.9 t 0.2 f P(U ) 1 R1 P(R ) 1 R0 0.3 f 0.7 t 0.9 t 0.2 f P(U ) 1 R1 P(R ) 1 R0 0.3 f 0.7 t 0.9 t 0.2 f P(U ) 1 R1 P(R ) 1 R0 0.9 t 0.2 f P(U ) 1 R1 0.3 f 0.7 t P(R ) 1 R0 0.9 t 0.2 f P(U ) 1 R1 0.3 f 0.7 t P(R ) 1 R0 Rain0 0.7 P(R )0 Umbrella2 Rain3 Umbrella3 Rain4 Umbrella4 Rain5 Umbrella5 Rain6 Umbrella6 Rain7 Umbrella7 Rain2 Problem: inference cost for each update grows with t Rollup filtering: add slice t + 1, “sum out” slice t using variable elimination Largest factor is O(d n+1 ), update cost O(d n+2 ) (cf. HMM update cost O(d 2n )) Chapter 15, Sections 1–5 34 Likelihood weighting for DBNs Set of weighted samples approximates the belief state Rain1 Umbrella1 Rain0 Umbrella2 Rain3 Umbrella3 Rain4 Umbrella4 Rain5 Umbrella5 Rain2 LW samples pay no attention to the evidence! ⇒ fraction “agreeing” falls exponentially with t ⇒ number of samples required grows exponentially with t 0 0.2 0.4 0.6 0.8 1 0 5 10 15 20 25 30 35 40 45 50 RMS error Time step LW(10) LW(100) LW(1000) LW(10000) Chapter 15, Sections 1–5 35 Particle filtering Basic idea: ensure that the population of samples (“particles”) tracks the high-likelihood regions of the state-space Replicate particles proportional to likelihood for et false true (a) Propagate (b) Weight (c) Resample Raint Raint +1 Raint +1 Raint +1 Widely used for tracking nonlinear systems, esp. in vision Also used for simultaneous localization and mapping in mobile robots 10 5 -dimensional state space Chapter 15, Sections 1–5 36

-sensor model P(EX) Particle filtering performance Resample to obtainopains proprtinal to W()=P(e)N( ne consistent at time t:N(x)/N=P(xe Particle filtering contd
Particle filtering contd. Assume consistent at time t: N(xt |e1:t)/N = P(xt |e1:t) Propagate forward: populations of xt+1 are N(xt+1|e1:t) = ΣxtP(xt+1|xt)N(xt |e1:t) Weight samples by their likelihood for et+1: W(xt+1|e1:t+1) = P(et+1|xt+1)N(xt+1|e1:t) Resample to obtain populations proportional to W: N(xt+1|e1:t+1)/N = αW(xt+1|e1:t+1) = αP(et+1|xt+1)N(xt+1|e1:t) = αP(et+1|xt+1)ΣxtP(xt+1|xt)N(xt |e1:t) = α P 0 (et+1|xt+1)ΣxtP(xt+1|xt)P(xt |e1:t) = P(xt+1|e1:t+1) Chapter 15, Sections 1–5 37 Particle filtering performance Approximation error of particle filtering remains bounded over time, at least empirically—theoretical analysis is difficult 0 0.2 0.4 0.6 0.8 1 0 5 10 15 20 25 30 35 40 45 50 Avg absolute error Time step LW(25) LW(100) LW(1000) LW(10000) ER/SOF(25) Chapter 15, Sections 1–5 38 Summary Temporal models use state and sensor variables replicated over time Markov assumptions and stationarity assumption, so we need – transition modelP(Xt |Xt−1) – sensor model P(Et |Xt) Tasks are filtering, prediction, smoothing, most likely sequence; all done recursively with constant cost per time step Hidden Markov models have a single discrete state variable; used for speech recognition Kalman filters allow n state variables, linear Gaussian, O(n 3 ) update Dynamic Bayes nets subsume HMMs, Kalman filters; exact update intractable Particle filtering is a good approximate filtering algorithm for DBNs Chapter 15, Sections 1–5 39