
Best-first search INFORMED SEARCH ALGORITHMS Expand most desirable unexpanded node fringe is a queue sorted in decreasing order of desirability CHAPTER 4,SECTIONS 1-2 Special cases: Outline Romania with step costs in km ◇Best-first search ◇A search ◇Heuristics 445 Review:Tree search Greedy search Evaluation function()(heuristic) =estimate of cost fromnto the closest goa empty then return failure Egs(n)=straight-line distance fromnto Bucharest eeds return nod Greedy search expands the node that appears to be closest to goal Astrategy is defined by picking the order of node expansion
Informed search algorithms Chapter 4, Sections 1–2 Chapter 4, Sections 1–2 1 Outline ♦ Best-first search ♦ A ∗ search ♦ Heuristics Chapter 4, Sections 1–2 2 Review: Tree search function Tree-Search( problem, fringe) returns a solution, or failure fringe ← Insert(Make-Node(Initial-State[problem]),fringe) loop do if fringe is empty then return failure node ←Remove-Front(fringe) if Goal-Test[problem] applied to State(node) succeeds return node fringe ← InsertAll(Expand(node, problem),fringe) A strategy is defined by picking the order of node expansion Chapter 4, Sections 1–2 3 Best-first search Idea: use an evaluation function for each node – estimate of “desirability” ⇒ Expand most desirable unexpanded node Implementation: fringe is a queue sorted in decreasing order of desirability Special cases: greedy search A ∗ search Chapter 4, Sections 1–2 4 Romania with step costs in km Bucharest Giurgiu Urziceni Hirsova Eforie Neamt Oradea Zerind Arad Timisoara Lugoj Mehadia Dobreta Craiova Sibiu Fagaras Pitesti Rimnicu Vilcea Vaslui Iasi Straight−line distance to Bucharest 0 160 242 161 77 151 241 366 193 178 253 329 80 199 244 380 226 234 374 98 Giurgiu Urziceni Hirsova Eforie Neamt Oradea Zerind Arad Timisoara Lugoj Mehadia Dobreta Craiova Sibiu Fagaras Pitesti Vaslui Iasi Rimnicu Vilcea Bucharest 71 75 118 111 70 75 120 151 140 99 80 97 101 211 138 146 85 90 98 142 92 87 86 Chapter 4, Sections 1–2 5 Greedy search Evaluation function h(n) (heuristic) = estimate of cost from n to the closest goal E.g., hSLD(n) = straight-line distance from n to Bucharest Greedy search expands the node that appears to be closest to goal Chapter 4, Sections 1–2 6
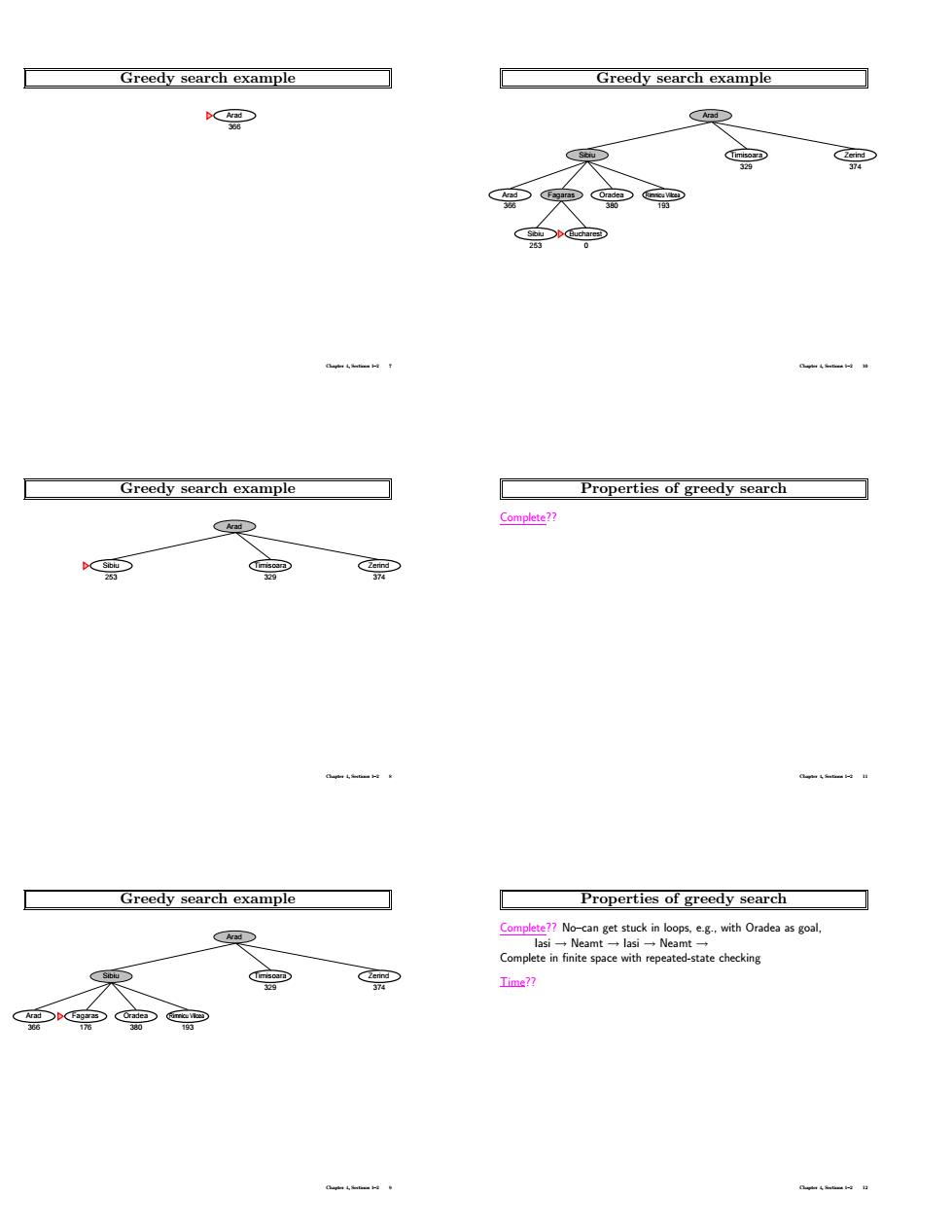
Greedy search example earch example Greedy search example Properties of greedy search Greedy search example Properties of greedy search Time?7
Greedy search example Arad 366 Chapter 4, Sections 1–2 7 Greedy search example Zerind Arad Sibiu Timisoara 253 329 374 Chapter 4, Sections 1–2 8 Greedy search example Rimnicu Vilcea Zerind Arad Sibiu Arad Fagaras Oradea Timisoara 329 374 366 176 380 193 Chapter 4, Sections 1–2 9 Greedy search example Rimnicu Vilcea Zerind Arad Sibiu Arad Fagaras Oradea Timisoara Sibiu Bucharest 329 374 366 380 193 253 0 Chapter 4, Sections 1–2 10 Properties of greedy search Complete?? Chapter 4, Sections 1–2 11 Properties of greedy search Complete?? No–can get stuck in loops, e.g., with Oradea as goal, Iasi → Neamt → Iasi → Neamt → Complete in finite space with repeated-state checking Time?? Chapter 4, Sections 1–2 12

Properties of greedy search A'search dea:avoid expanding paths that are already expensive Evaluation function f(n)) al from Space?? (Alo rquire()for any goal C.) Enever overestimates the actuaroad distance Properties of greedy search A'search example Time??O().but a good heuristic can give dramatic improvement Space??O()-keeps all nodes in memory Optimal7? Properties of greedy search A search example 之 im7)butagod heuristic cangvdramatic improvement 品 Space??nodes in memory Optimal7?No
Properties of greedy search Complete?? No–can get stuck in loops, e.g., Iasi → Neamt → Iasi → Neamt → Complete in finite space with repeated-state checking Time?? O(b m), but a good heuristic can give dramatic improvement Space?? Chapter 4, Sections 1–2 13 Properties of greedy search Complete?? No–can get stuck in loops, e.g., Iasi → Neamt → Iasi → Neamt → Complete in finite space with repeated-state checking Time?? O(b m), but a good heuristic can give dramatic improvement Space?? O(b m)—keeps all nodes in memory Optimal?? Chapter 4, Sections 1–2 14 Properties of greedy search Complete?? No–can get stuck in loops, e.g., Iasi → Neamt → Iasi → Neamt → Complete in finite space with repeated-state checking Time?? O(b m), but a good heuristic can give dramatic improvement Space?? O(b m)—keeps all nodes in memory Optimal?? No Chapter 4, Sections 1–2 15 A∗ search Idea: avoid expanding paths that are already expensive Evaluation function f(n) = g(n) + h(n) g(n) = cost so far to reach n h(n) = estimated cost to goal from n f(n) = estimated total cost of path through n to goal A ∗ search uses an admissible heuristic i.e., h(n) ≤ h ∗ (n) where h ∗ (n) is the true cost from n. (Also require h(n) ≥ 0, so h(G) = 0 for any goal G.) E.g., hSLD(n) never overestimates the actual road distance Theorem: A ∗ search is optimal Chapter 4, Sections 1–2 16 A∗ search example Arad 366=0+366 Chapter 4, Sections 1–2 17 A∗ search example Zerind Arad Sibiu Timisoara 393=140+253 447=118+329 449=75+374 Chapter 4, Sections 1–2 18

A'search example A'search example a 2 盒篇黑 2e D(C a4。 A search example Optimality of A(standard proof) e 立思 (Ga)=(Ga)since h(G2)=0 Since f((n).Awill never sect for A'search example Optimality of A'(more useful) Lemma:Aexpands nodes in order of 典 2 点宗会点
A∗ search example Zerind Arad Sibiu Arad Timisoara Fagaras Oradea Rimnicu Vilcea 447=118+329 449=75+374 646=280+366 415=239+176 671=291+380 413=220+193 Chapter 4, Sections 1–2 19 A∗ search example Zerind Arad Sibiu Arad Timisoara Fagaras Oradea 447=118+329 449=75+374 646=280+366 415=239+176 Rimnicu Vilcea Craiova Pitesti Sibiu 526=366+160 417=317+100 553=300+253 671=291+380 Chapter 4, Sections 1–2 20 A∗ search example Zerind Arad Sibiu Arad Timisoara Sibiu Bucharest Fagaras Oradea Rimnicu Vilcea Craiova Pitesti Sibiu 447=118+329 449=75+374 646=280+366 591=338+253 450=450+0 526=366+160 417=317+100 553=300+253 671=291+380 Chapter 4, Sections 1–2 21 A∗ search example Zerind Arad Sibiu Arad Timisoara Sibiu Bucharest Fagaras Oradea Rimnicu Vilcea Craiova Pitesti Sibiu Bucharest Craiova Rimnicu Vilcea 418=418+0 447=118+329 449=75+374 646=280+366 591=338+253 450=450+0 526=366+160 553=300+253 615=455+160 607=414+193 671=291+380 Chapter 4, Sections 1–2 22 Optimality of A∗ (standard proof) Suppose some suboptimal goal G2 has been generated and is in the queue. Let n be an unexpanded node on a shortest path to an optimal goal G1. G n G2 Start f(G2) = g(G2) since h(G2) = 0 > g(G1) since G2 is suboptimal ≥ f(n) since h is admissible Since f(G2) > f(n), A ∗ will never select G2 for expansion Chapter 4, Sections 1–2 23 Optimality of A∗ (more useful) Lemma: A ∗ expands nodes in order of increasing f value∗ Gradually adds “f-contours” of nodes (cf. breadth-first adds layers) Contour i has all nodes with f = fi , where fi < fi+1 O Z A T L M D C R F P G B U H E V I N 380 400 420 S Chapter 4, Sections 1–2 24

Properties of A Properties of A Complete Yes.unless there are infinitely many nodes with() Space Keeps all nodes in memory Properties of A' Properties of A Complete??Yes, unle there are infinitely many nodes with() thereare infinitely many nodes with( Lime?? mExponential inrelativer inlngthofso Space??Keeps all nodes in memory <C Properties of A Proof of lemma:Consistency Complete??Yes.unless there are infinitely many nodes with f<f(G Aheuristic if Time??Exponential in [relative error in h x length of soln.] hn)≤cdm,a,n)+hM .we have c(n.a.n) a+h f Le(n)is nondecreasing alng any path
Properties of A∗ Complete?? Chapter 4, Sections 1–2 25 Properties of A∗ Complete?? Yes, unless there are infinitely many nodes with f ≤ f(G) Time?? Chapter 4, Sections 1–2 26 Properties of A∗ Complete?? Yes, unless there are infinitely many nodes with f ≤ f(G) Time?? Exponential in [relative error in h × length of soln.] Space?? Chapter 4, Sections 1–2 27 Properties of A∗ Complete?? Yes, unless there are infinitely many nodes with f ≤ f(G) Time?? Exponential in [relative error in h × length of soln.] Space?? Keeps all nodes in memory Optimal?? Chapter 4, Sections 1–2 28 Properties of A∗ Complete?? Yes, unless there are infinitely many nodes with f ≤ f(G) Time?? Exponential in [relative error in h × length of soln.] Space?? Keeps all nodes in memory Optimal?? Yes—cannot expand fi+1 until fi is finished A ∗ expands all nodes with f(n) C ∗ Chapter 4, Sections 1–2 29 Proof of lemma: Consistency A heuristic is consistent if n c(n,a,n’) h(n’) h(n) G n’ h(n) ≤ c(n, a, n 0 ) + h(n 0 ) If h is consistent, we have f(n 0 ) = g(n 0 ) + h(n 0 ) = g(n) + c(n, a, n 0 ) + h(n 0 ) ≥ g(n) + h(n) = f(n) I.e., f(n) is nondecreasing along any path. Chapter 4, Sections 1–2 30

Admissible heuristics Relaxed problems Eg.for the 8-puzzle If the rules of the 8-puzzle are relaxed so that a tile can move anywhere (i.e.,no.of squares from des location of each tile) then)gives the shortest solution ⑦24 123 If the rules are relaxed so that a tile can move to any adjacent square 456 then ha(n)gives the shortest solution 83 78 roblem Admissible heuristics Relaxed problems contd. Egfor the 8-puzzle (i.e.no.of squares from desired location of each tile) 24 456 78 8043431404241=4 Minimum spanning tree can be computed in (n and is a lower bound on the shortest(open)tou Dominance Summary Heuristic functions estimate costs of shortest paths Good heuristics can dramatically reduce search cos Typical search costs: Greedy best-first search expands lowest -incomplete and not always optimal d=241D5≈54.000.000.000nods Admissible heuristics can be derived from exact solution of relaxed problem Given any admissible heuristics h(n)=max(ha(n).ho(n)) is also admissible and dominates
Admissible heuristics E.g., for the 8-puzzle: h1(n) = number of misplaced tiles h2(n) = total Manhattan distance (i.e., no. of squares from desired location of each tile) 2 Start State Goal State 51 3 4 6 7 8 5 1 2 3 4 6 7 8 5 h1(S) =?? h2(S) =?? Chapter 4, Sections 1–2 31 Admissible heuristics E.g., for the 8-puzzle: h1(n) = number of misplaced tiles h2(n) = total Manhattan distance (i.e., no. of squares from desired location of each tile) 2 Start State Goal State 51 3 4 6 7 8 5 1 2 3 4 6 7 8 5 h1(S) =?? 6 h2(S) =?? 4+0+3+3+1+0+2+1 = 14 Chapter 4, Sections 1–2 32 Dominance If h2(n) ≥ h1(n) for all n (both admissible) then h2 dominates h1 and is better for search Typical search costs: d = 14 IDS = 3,473,941 nodes A ∗ (h1) = 539 nodes A ∗ (h2) = 113 nodes d = 24 IDS ≈ 54,000,000,000 nodes A ∗ (h1) = 39,135 nodes A ∗ (h2) = 1,641 nodes Given any admissible heuristics ha, hb , h(n) = max(ha(n), hb(n)) is also admissible and dominates ha, hb Chapter 4, Sections 1–2 33 Relaxed problems Admissible heuristics can be derived from the exact solution cost of a relaxed version of the problem If the rules of the 8-puzzle are relaxed so that a tile can move anywhere, then h1(n) gives the shortest solution If the rules are relaxed so that a tile can move to any adjacent square, then h2(n) gives the shortest solution Key point: the optimal solution cost of a relaxed problem is no greater than the optimal solution cost of the real problem Chapter 4, Sections 1–2 34 Relaxed problems contd. Well-known example: travelling salesperson problem (TSP) Find the shortest tour visiting all cities exactly once Minimum spanning tree can be computed in O(n 2 ) and is a lower bound on the shortest (open) tour Chapter 4, Sections 1–2 35 Summary Heuristic functions estimate costs of shortest paths Good heuristics can dramatically reduce search cost Greedy best-first search expands lowest h – incomplete and not always optimal A ∗ search expands lowest g + h – complete and optimal – also optimally efficient (up to tie-breaks, for forward search) Admissible heuristics can be derived from exact solution of relaxed problems Chapter 4, Sections 1–2 36