
9 HLdVHO ONIAVId HNVO
ying pla Game 6 Chapter 1 6 Chapter

9 anduyD uonewjojul 1ajadwl jo sawe ueyo jo sawe9◇ uonenjena anewixoudde pue siw!l aonosey 3ulunud g-o- suolslpap xewlulw Kejd ajed◇ sewes◇ aurlinO
Outline Games ♦ y pla erfect P ♦ decisions minimax – runing p β– α – evaluation ximate ro app and limits Resource ♦ chance of Games ♦ rmation info erfect imp of Games ♦ 2 6 Chapter

g 9 (9S6IK4μe)W)ypueas Jada∂o Molle o,3uunid● (Lg-Zg6T 'Janwes)Aoeunope uonenjena anodw!01 Suueal aulypew (IG6T '3uunL)we3oud ssayp 1s! (0S6L‘uouueyS 86I u!Mgt6I'asnz)uonenjena aewxodde 'uozuoyu!. (b6t‘uuewnaN uoA:ZI6I‘o13wuBZ)Ke1dpy3 d joj wyo3● (9t8I 'aeqqeg)Kejd yo saull ajqissod suapisuoo jaindwo). :ypene jo ueld a1 ewixodde asnw'eo3puyO1 x!jun←s4w川auL Kjde quauoddo ajqissod Kene Joy enow e BuiKyads ens e s!uonnjosquauoddo qe!paudun, swalqod yolees 'sA sowes
problems h searc vs. Games strategy a is solution ⇒ onent opp redictable” “Unp reply onent opp ossible p every r fo move a ecifying sp ximate ro app must goal, find to ely unlik ⇒ limits Time attack: of Plan 1846) (Babbage, y pla of lines ossible p considers Computer • 1944) Neumann, on V 1912; (Zermelo, y pla erfect p r fo rithm Algo • 1948; Wiener, 1945; (Zuse, evaluation ximate ro app rizon, ho Finite • 1950) Shannon, 1951) uring, (T rogram p chess First • 1952–57) (Samuel, accuracy evaluation rove imp to rning lea Machine • 1956) , rthy (McCa rch sea er deep w allo to Pruning • 3 6 Chapter
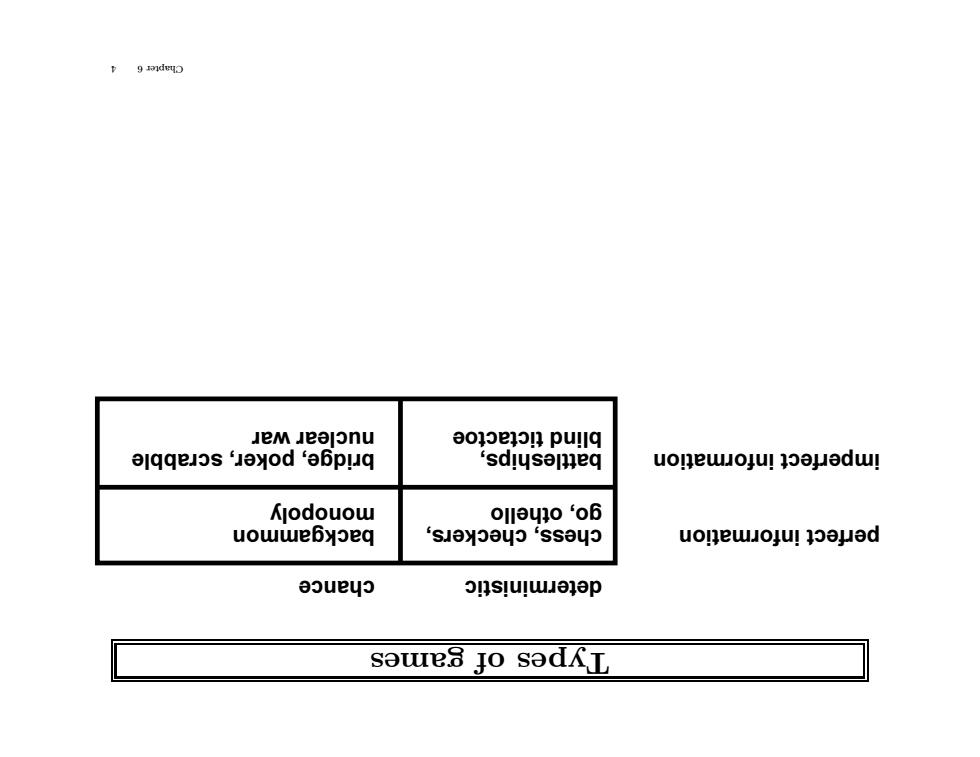
p9 deD JeM Jeelonu a0oe4 on pu川川q 1 qqejos'leyod 'a6pμq ‘sdl叫semneq uonewoju!1pμdu Kjodouow 0y10‘o6 uowwebyoeq sJeyoayo‘sseyo uonewJoju!350.μad eoueyo s!ulwμe1p sowes jo sedL
games of es yp T chance deterministic perfect information imperfect information chess, checkers, go, othello backgammon monopoly bridge, poker, scrabble nuclear war battleships, blind tictactoe 4 6 Chapter
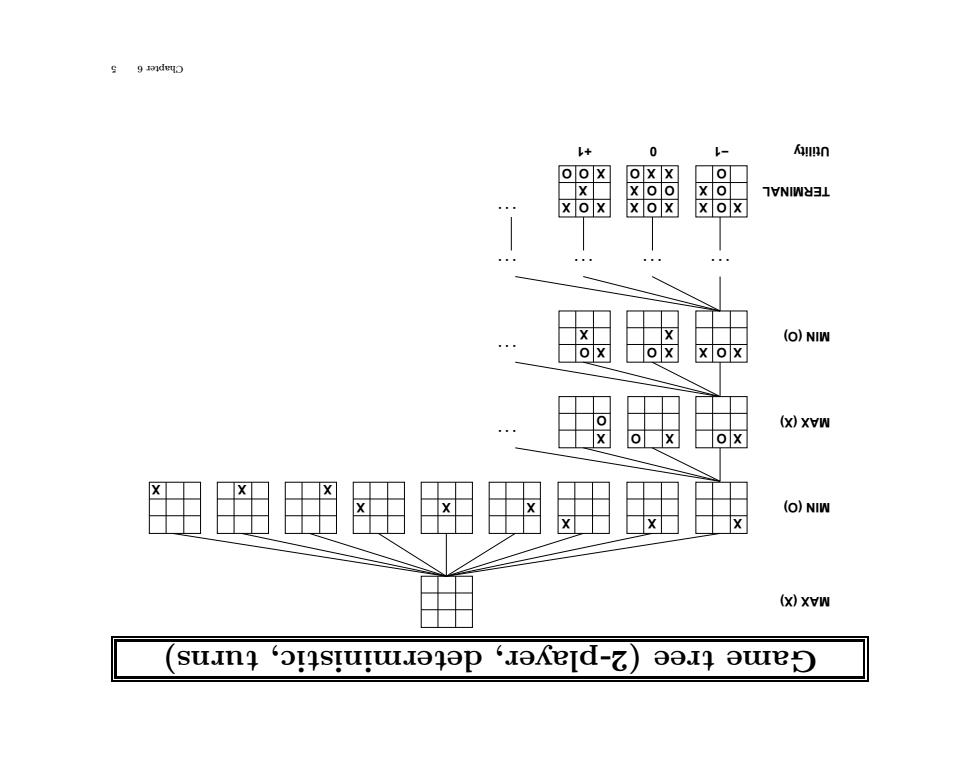
+ 0 - Aunn xo可 xo☒ x 1VNIWX31 X o X X o X X (O)NIW o X X ox o (x)xVW ox (O)NIW (x)xVW suing‘oIsIuIwIoqop ‘IOKeld-乙) 001 owe
turns) deterministic, er, y (2-pla tree Game X X X X X X X X X MAX (X) MIN (O) X X O O O O X O O O O O O MAX (X) O X O X X O X X X X X X X MIN (O) X O X X O X X O X . . . . . . . . . . . . . . . . . . . . . TERMINAL X X +1 0 −1 Utility 5 6 Chapter

99md3 8 ZL 乙 乙 NI E XVW aue8d-乙83 Keld isaq isulee yoKed ajqenalype isaq enjen xewlulw asay3ly ym uon!sod 0n anow asooyp :eap] sewe8 uonewojul-1pajad 'nslulwjenep oj Keld 15ajed xewluN
Minimax games rmation erfect-info p deterministic, r fo y pla erfect P value minimax highest with osition p to move ose cho Idea: y pla est b against off y pa achievable est b = game: 2-ply E.g., MAX 2 5 14 6 4 2 8 12 3 MIN 3 A 1 A 3 A 2 A 13 A 12 A 11 A 21 A 23 A 22 A 33 A 32 A 31 2 2 3 6 6 Chapter

n uIngoI ((s)anTVA-XVW 'Q)NIN-op (s)sHossaoons u!s 'D o] 0o→n (707s)xLILO uIn3oI uoq (707S)ISHL-IVNINHL J! anjoa fippign D suIngoI (1D)s)anIVA-NIW uonounJ n umjoI ((s)anIVA-NIWN 'Q)XVW-op (ans)sHossaoons u!s 'D o] 00-→ (107s)xLITILO uIngox uoy?(7DS)ISHL-IVNIWHL J! angoa fippgn D suingoI(ans)anIVA-XVW uoqoun] ((an0)s ')LInSad)nIVA-NIW BuIzIwIxew (ns)SNOILOV u!D ay1 umngaI awe3 ul anens quauno'ag0gs :sandur uo2goD uD sumngoI (Ds)NOISIO(-XVWINIW uoIqoung wqo8e xewu!N
algorithm Minimax action an returns ) state ( Minimax-Decision function game in state current , state : inputs )) state , a( t Resul ( alue Min-V maximizing ) state ( ctions A in a the return value utility a returns ) state ( alue Max-V function ) state ( Utility return then ) state ( Terminal-Test if −∞ ←v )) s( alue Min-V , v( Max ←v do ) state ( Successors in s a, for v return value utility a returns ) state ( alue Min-V function ) state ( Utility return then ) state ( Terminal-Test if ∞ ←v )) s( alue Max-V , v( Min ←v do ) state ( Successors in s a, for v return 7 6 Chapter

8 9 de iieajdwo) xewruru jo serodoId
minimax of erties Prop ?? Complete 8 6 Chapter

69d iilewndO jaa alluyu!ue u!uana asixa ue KBenens alluy e gN (s!y oy seln oy!ads sey ssayp)auy s!Ajuo Liaajdwo xewruru jo serqodoId
minimax of erties Prop this). r fo rules ecific sp has (chess finite is tree if Only ?? Complete tree! infinite an in even exist can strategy finite a NB ?? Optimal 9 6 Chapter

OI 9 adeyD iKxajdwo awl iiasIMayO'quauoddo jewndo ue isulee 'sa iilewndO (siya joj sajnu oylpads sey ssayp)anluy s!aan j!'sa iianajdwo) xewrurw jo sangodod
minimax of erties Prop this) r fo rules ecific sp has (chess finite is tree if es, Y ?? Complete Otherwise?? onent. opp optimal an against es, Y ?? Optimal ?? y complexit Time 10 6 Chapter