
9I HLVHO SNOISIOHI IVNOILVY
decisions tional Ra 16 Chapter 1 16 Chapter
uolewJoju!o3neΛ◇ Sμ04 u uoIs1P30◇ s31l4n31nque41nW◇ KuoW◇ s3l4n◇ s3u3 gad jeuor4eH◇ ourino
Outline references p Rational ♦ Utilities ♦ Money ♦ utilities Multiattribute ♦ rks ow net Decision ♦ rmation info of alue V ♦ 2 16 Chapter
9I adeyD Ko1 pauajaud 1ou g axv pue uaamnaq aouaajj!pu! &~/ 9o1 pauejaud a</ :uonenoN d-I [a‘(d-)yd=Tu4o7 d s3zIμduIeμeoun yaIM suoI1ens3!‘s3μo1pue(3a‘/)s3zud8 uowe s3 sooy1ue8euV seoualojeld
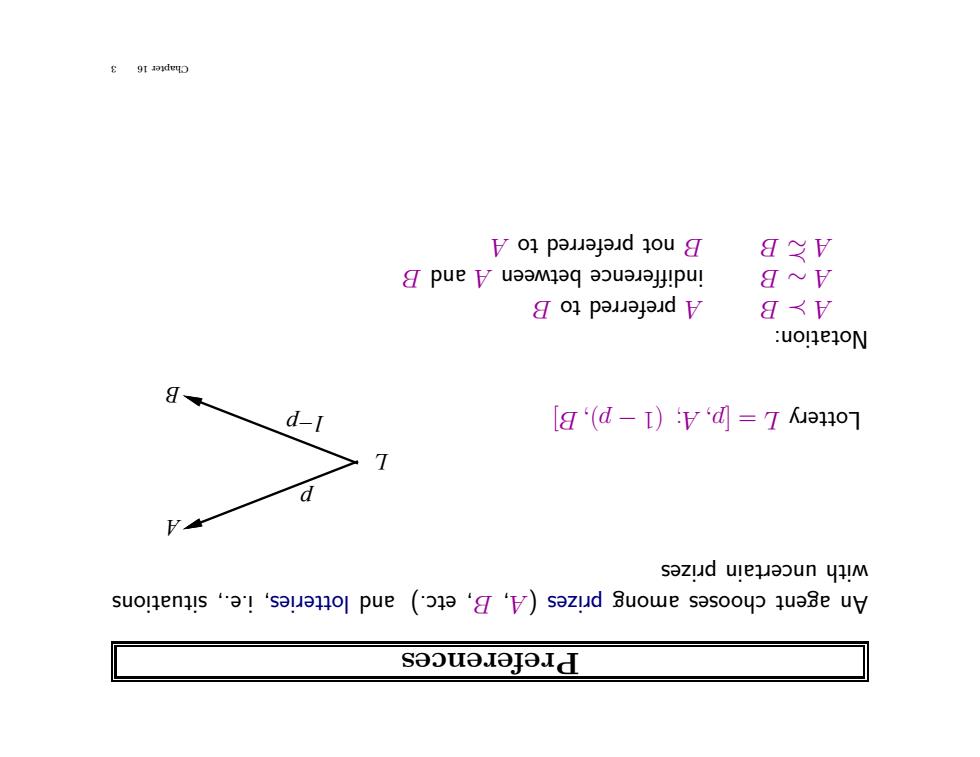
Preferences situations i.e., , lotteries and etc.) , B, A( rizes p among oses cho agent An rizes p uncertain with ] B,) p − (1 ; A p, [ = L Lottery L p 1−p A B Notation: B to referred p A B A B and A een wet b indifference B ∼ A A A to referred p not B B ∼ 3 16 Chapter

(ab-IVbX[ad-IVd台b<d←a<y KluonouoW [Od-[ad~[Od-LVd←8~/ K4μqen4!4sqnS g~o'd-1vd dE =0383V Kinunuo) (O</)=(0<a)V(a<) KsueL (a~V)∧(H<a)A(a<V) K!qepO :squlensuo) Kn panpadxa jo uoneziwixew se a]qequosap JoIneyaq ←s3u3Bed1euo4e squlensuoo Kaqo isnw quage jeuolel e jo seoualajald :eapl sooualajaId leuo!ey
preferences Rational constraints. ey ob must agent rational a of references p Idea: ⇒ references p Rational y utilit ected exp of maximization as describable r ehavio b Constraints: y Orderabilit ) B ∼ A( ∨) A B( ∨) B A( y ransitivit T ) C A( ⇒) C B( ∧) B A( y Continuit B ∼] C p, −1 ; A p, [ p ∃ ⇒ C B A y Substitutabilit ] C p, −1; B p, [ ∼] C p, −1 ; A p, [ ⇒ B ∼ A y Monotonicit ] B p, −1 ; A p, [ ⇔q ≥p( ⇒ B A ]) B, q −1 ; A, q[ ∼ 4 16 Chapter
9I adeyo 13 01 qua I (Kes)Ked pinom 01 sey oym quae ue uay Jl 133 01 u I(Kes)Ked pinom g sey oym quage ue uay'g 1301 u I (Kes)Ked pinom sey oym quaRe ue uay 'gl Kauow si e Keme nI8o1 paonpul aq ueo saouajajad anllsuenul yhlm quage ue :a]dwexe joy Keuonejl quapIna-jJas on speal squlensuoo ayn gunejo! 'pquoo sooualojold leuorey
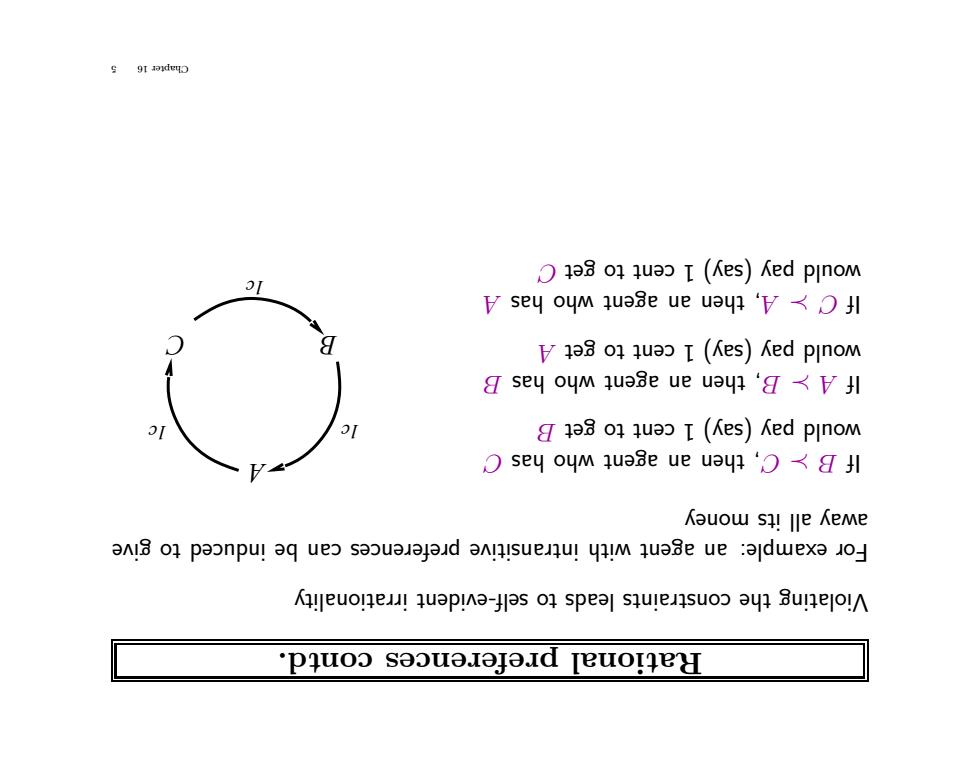
td. con preferences Rational y irrationalit self-evident to leads constraints the Violating give to induced eb can references p intransitive with agent an example: r oF money its all ya wa C has who agent an then , C B If B get to cent 1 y) (sa y pa ould w B has who agent an then , B A If A get to cent 1 y) (sa y pa ould w A has who agent an then , A C If C get to cent 1 y) (sa y pa ould w A C B 1c 1c 1c 5 16 Chapter

aoen 1ajad joy ajqen dnyool e" san!liqeqoud pue san!n Sune]ndiuew o Sunuasauda Jana inoyim (n3W yiIM quansisuo)jeuone Kjaunua aq ueo quage ue :anoN Ki!n panpadxe saziwixew leyn uonpe ay1 asooy) a1 dipuud∩]W (S)nd=(Swd:·std)n axF÷(a)n<()n neyl yons uonouny panjen-jeal e sisixa alay squesuoo ay uKsnes saoualejed uSn!S :(t6I 'usua3oW pue uuewneN uOA :IE6I Kaswey)woIouL K!an paqoadxe Surzrwxew
y utilit ected exp Maximizing 1944): rgenstern, Mo and Neumann von 1931; , (Ramsey Theorem constraints the satisfying references p Given that such U function real-valued a exists there A ⇔ ) B( U ≥) A( U B ∼ )i S( Ui pi Σ = ]) n S, np ; . . . ; 1 S, 1 p([ U : rinciple p MEU y utilit ected exp maximizes that action the ose Cho MEU) with (consistent rational entirely eb can agent an Note: robabilities p and utilities manipulating r o resenting rep ever without e tictacto erfect p r fo table okup lo a E.g., 6 16 Chapter
L 9I deo yieap juegsu! 1000000 ~0$ed elojeq se anunuoo 6666660 un d qeqoud o asn.pe (d-I)Aqeqoud yim Tn aydonsee alq!ssod 1sJom,, d4μqeqo1d4m⊥n,3zμd31 qissod as3q, sey aeyd Kano piepuens eo aes uanl3 e aeduo :san uewny jo quawssasse o1 ypeodde pepues isuaqwnu yolyM 'slaqwnu jea on sanens dew sal!!n sor!1!40
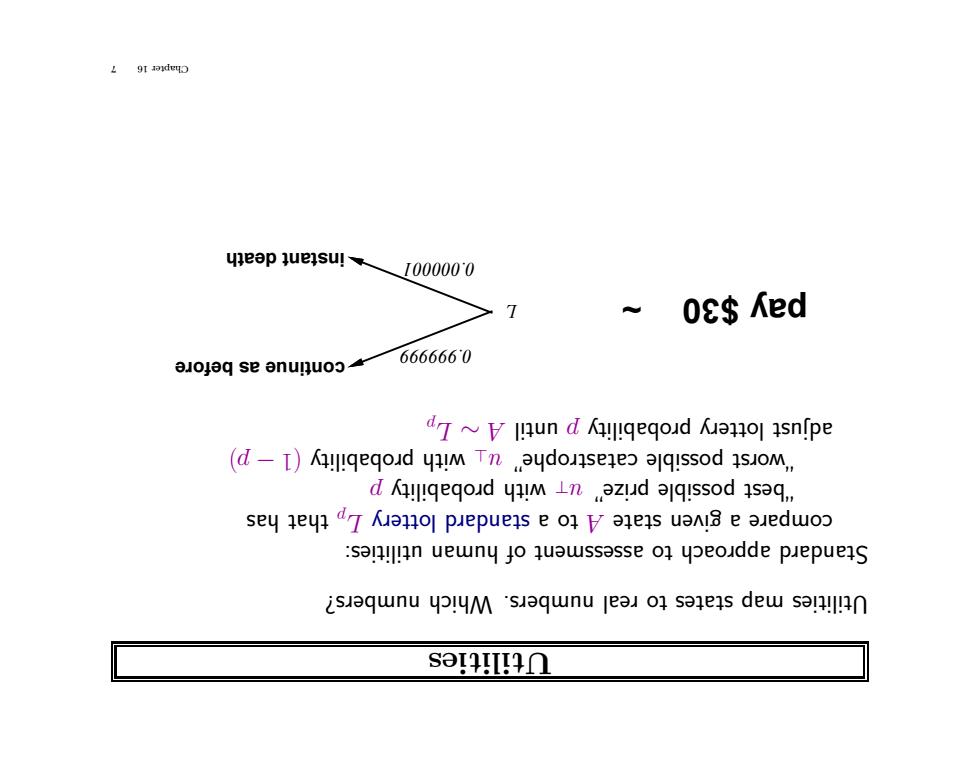
Utilities ers? numb Which ers. numb real to states map Utilities utilities: human of assessment to roach app rd Standa has that p L lottery rd standa a to A state given a re compa p y robabilit p with >u rize” p ossible p est “b ) p − (1 y robabilit p with ⊥u catastrophe” ossible p rst o “w p L ∼ A until p y robabilit p lottery adjust L 0.999999 0.000001 continue as before instant death ~ pay $30 7 16 Chapter

s3 zud uo Jap0Ieo13!‘p3 ulwJanep3queK!n jeu!pio Kuo‘(s3I1o4p人uB44o1ou)uos3zμd onsiulwa1p4hM 0<y4My+(r)ay=(r),0 uonewjojsuen jeaull an+1'M quer.Ieaur sI JoIneyaq :anoN ysu jenuensqns Suinjonu!suois!pap jeoipaw oj njasn se3Ka川pa4 sn.pe-a!enb:s人TVO 'sysu 1onpoud aonpa o1 3uKed'no ue!ssny o]Injasn 44e∂po3ueyp44uoW-3uo:sμouo5IW 0'0 Tn '0'I In :san!ln paz!lewoN soleos Au!40
scales y Utilit 0. 0 = ⊥u, 0. 1 = >u : utilities rmalized No death of chance one-millionth : rts Micromo etc. risks, duct ro p reduce to ying pa roulette, Russian r fo useful rs ea y life y-adjusted qualit : Ys QAL risk substantial involving decisions medical r fo useful rmation transfo r linea +ve w.r.t. t arian v in is r ehavio b Note: U0 0 >1 k where 2 k +) x( U1 k =) x( only choices), lottery (no only rizes p deterministic With rizes p on rder o total i.e., determined, eb can y utilit rdinal o 8 16 Chapter
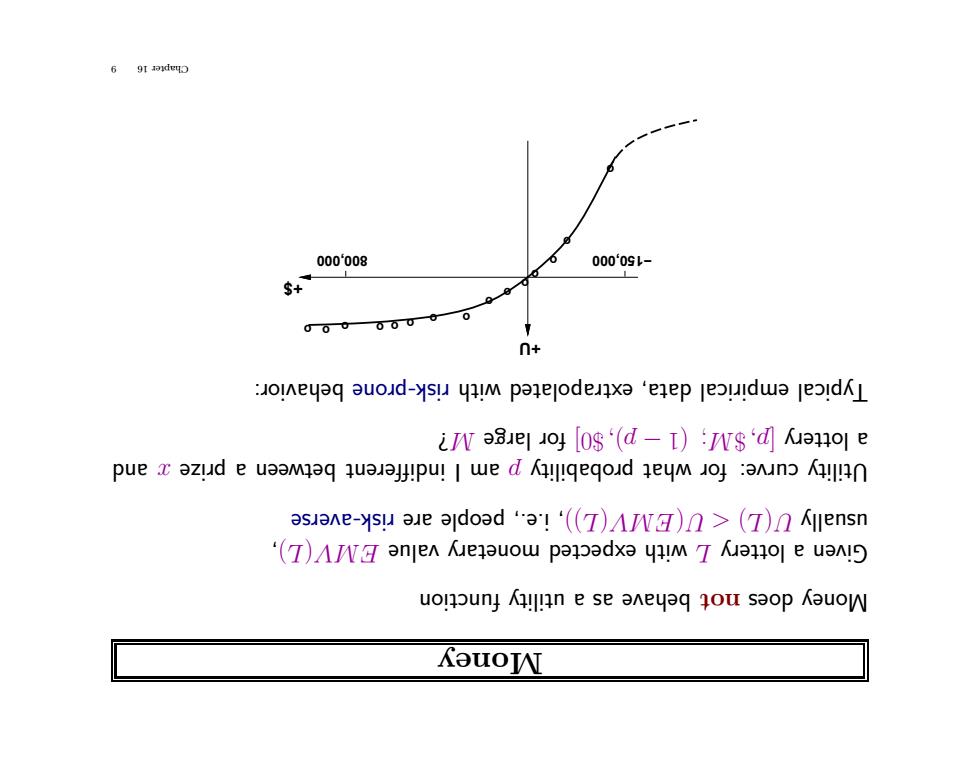
6 9I adeyD 000'008 00009l- 000000 n+ :JoIneyaq auod-ysu yiIm parejodenxa 'enep jeouldwa jeoidKL in auelo [0s'(d-I):ws'd Kanol e pue x azud e ueamaq quauaj!pu!I we d qeqoud eym oj :ann ase-su3e∂ldo3d3!‘(T)AJN☑)n>(T)Kjlensn (T)I anjen Kenauow panpadxa yM T Kanol e uanlS uonouny Kn e se aneyaq qou saop KauoW KouoN
Money function y utilit a as ehave b not es do Money ,) L( V ME value ry moneta ected exp with L lottery a Given risk-averse re a eople p i.e., , )) L( V ME( U <) L( U usually and x rize p a een wet b indifferent I am p y robabilit p what r fo curve: y Utilit ? M rge la r fo $0] ,) p − (1 ; M$ p, [ lottery a r: ehavio b rone risk-p with olated extrap data, empirical ypical T +U +$ 800,000 −150,000 o o o o o o o o o o o o o o o 9 16 Chapter
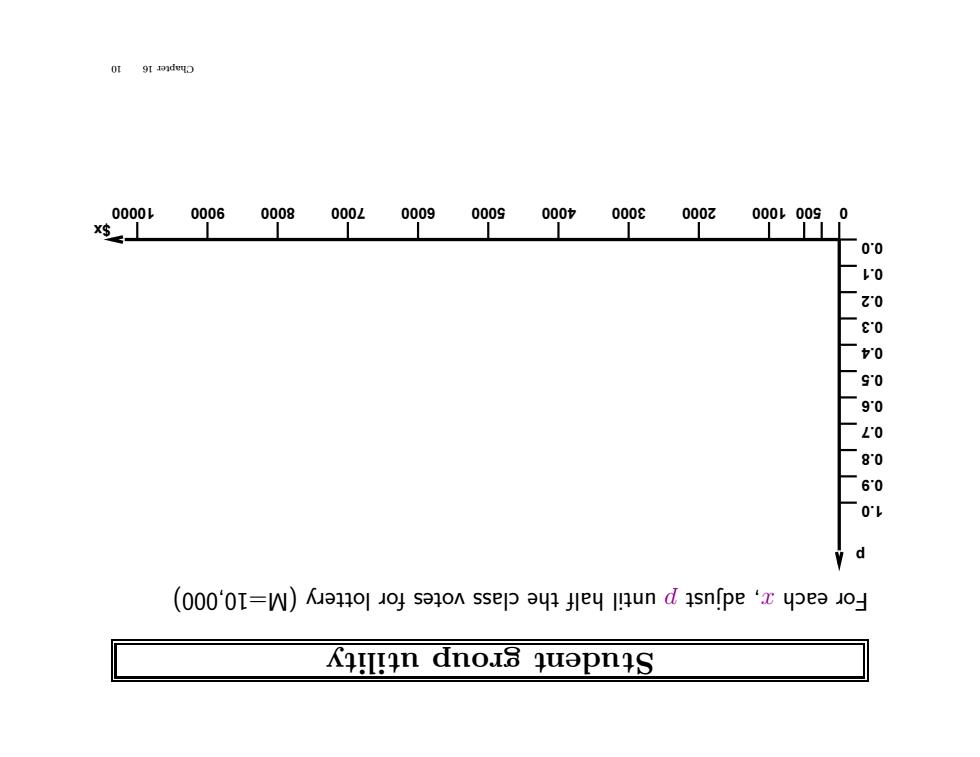
0000L 0006 0008 000 0009 0009 000 000E 000z 000L009 0 0^0 L'0 Zo E0 0 90 90 L'O 80 60 O'L (000'0I=W)ue4 ol 03 s34 OA ssep ayl jle叫I4 un d asnfpe‘x4pe3o」 Kiln dno3 quapniS
y utilit group t Studen (M=10,000) lottery r fo votes class the half until p adjust , x each r oF p $x 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 10000 9000 8000 7000 6000 5000 4000 3000 2000 1000 500 0 10 16 Chapter