
-I SNOILOHS O HLdVHO ONINHVHT IVOILSILVLS
learning tistical a St 1–3 Sections 20, Chapter 1 1–3 Sections 20, Chapter

乙8-1suo139S0元ndgD uoIssaa Jeaull enep anajdwoo yiIm Sulujeal Jaewejed TW 8 ulujea]au s3Ke8◇ Bulueal pooy!jay!l wnwixew pue uowa]sod e wnwixeW Sulue3 ueis3Ke9◇ aurlinO
Outline rning lea esian y Ba ♦ rning lea do eliho lik maximum and ri osterio p a Maximum ♦ rning lea net es y Ba ♦ data complete with rning lea rameter pa ML – regression r linea – 2 1–3 Sections 20, Chapter

8 g-I suopos '07 isisayiodKy ssan3-isaq auo yoid o1 paau oN (p4)d(4x)d=(p4)d(4'Px)d=(px)d :sasaynodKy ayl Jano aBeJane pany3iam-pooy!lay!l e asn suolo!pald pooy!lay!l ay palleo s!(yp)d ayM (4d(yp)do=(p4d Aulqeqoud Jouansod e sey sisaynodKy ypea 'ej os enep ayn uanl) Np·p=p enep Buiuien alqeuen wopue jo awooino ay1 san!3p uoneasqo yif (Hd oudy sanjen 'alqeuen sisaynodKy ay s!H apeds sisayiodKy ay1 Jano uonnquas!p Auqeqod e yo 3uepdn ueisaKeg se ulue Ma!A Suruleol uelsoxeg IInH
learning esian y Ba ull F distribution y robabilit p a of dating up esian y Ba as rning lea View space othesis hyp the over ) H( Pr rio p,. . . , 2 h, 1 h values riable, va othesis hyp the is H j D riable va random of outcome the gives j d observation th j Nd, . . . , 1 d =d data training y: robabilit p r osterio p a has othesis hyp each r, fa so data the Given )i h( P)i h| d( Pα =) d|i h( P do eliho lik the called is )i h| d( P where otheses: hyp the over average eighted d-w o eliho lik a use Predictions ) d|i h( P)i h| X( Pi Σ =) d|i h( P)i h, d| X( Pi Σ =) d| X( P othesis! hyp est-guess b one pick to need No 3 1–3 Sections 20, Chapter

g-I suonos '07 1deD iaq Kpueo axau ay IlM nonel ieyM i!s!eq jo puly ieyM ●●●●●●●●●●:8 eq awos woy umeup s3pue3u3 sqo am uay 8 salpue au!l %00I e %0I salpue aw!l %SL+salpue Kuayp %9 :y ae %0 salpue au!l %09+salpue Kuay %0g :y e %0 sa!pue aw!l %9+salpue Kuayp %SL:y e %0 salpue Kuay %00I :t e%0I :salpueo jo sBeq jo spuiy anly ae auay]asoddns odwexH
Example candies: of bags of kinds five re a there ose Supp candies cherry 100% : 1 h re a 10% candies lime 25% + candies cherry 75% : 2 h re a 20% candies lime 50% + candies cherry 50% : 3 h re a 40% candies lime 75% + candies cherry 25% : 4 h re a 20% candies lime 100% : 5 h re a 10% bag: some from wn dra candies observe e w Then e? b candy next the will flavour What it? is bag of kind What 4 1–3 Sections 20, Chapter
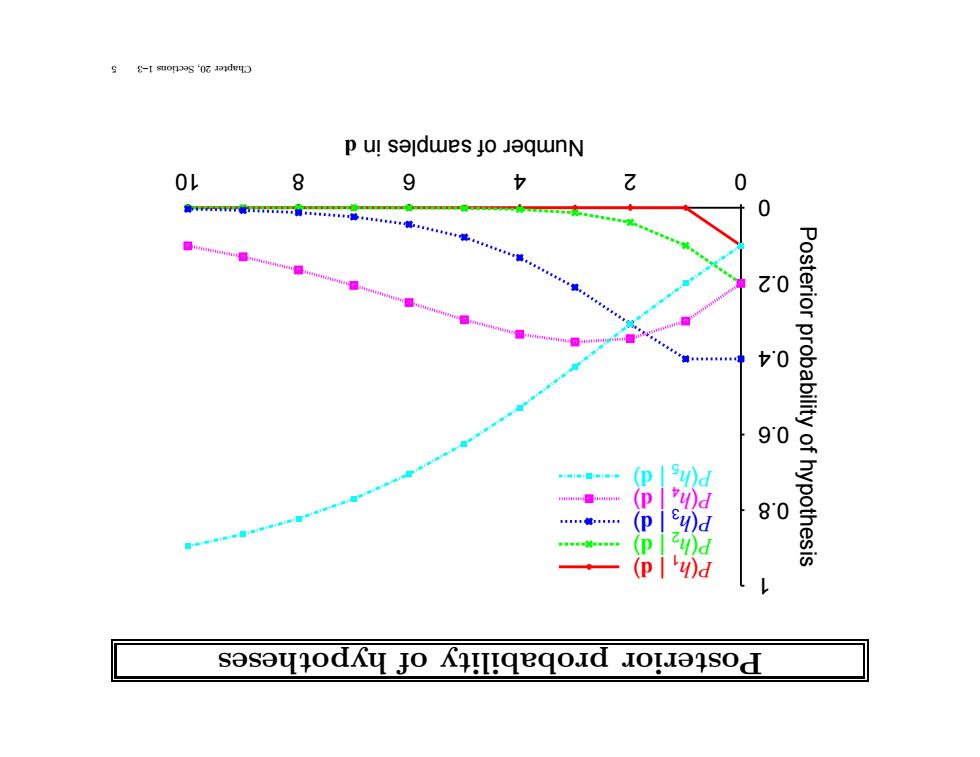
s g-I suonos '0 p u!sajdwes jo jaqwnN OL 8 9 b 乙 0 0 ◆ t0 9^0 (P su)d (P vy)d Posterior probability of hypothesis 制 (P a 80 (P d (P )d sasouodAy Jo Kil!qeqoid IoLonsod
otheses yp h of y probabilit osterior P 0 0.2 0.4 0.6 0.8 1 10 8 6 4 2 0 Posterior probability of hypothesis d Number of samples in ) d | 1 h( P ) d | 2 h( P ) d | 3 h( P ) d | 4 h( P ) d | 5 h( P 5 1–3 Sections 20, Chapter

98-1so139S0zdw3 p u!sajdwes jo JaqwnN OL 8 9 b 0 t0 90 90 P(next candy ㄥ0 8^0 lime 60 L Kuqeqoid uonopaId
y probabilit Prediction 0.4 0.5 0.6 0.7 0.8 0.9 1 10 8 6 4 2 0 P(next candy is lime | d ) d Number of samples in 6 1–3 Sections 20, Chapter

L 8-I suonoos'0 (aua!os o)sisaynodKy quasisuo sejdwls dVW asIMayo 0'uasisuo J!I s!(p)d 'sasaynodAy onslulwaap o Buiwe1(7qW)4h8ua1uoI4 duosap wnwluw jo eap!olseq o叫4s!sI4L sisaynodKy apooua o1 silq sisaynodKy uanl3 enep apooua o1 siiq (o annegau)se pamain aq ueo swjan 3o ()d 01+(p)d o1 o (4)d(p)d aziwixew "al (p 3uzwxew dyiy asooyp :uweal (dVW)Houosod e wnwixew (sainque 9 jo suonouny ueajoog 9I9'ISs'60L'ELO'L'9tt'8I) ajqepenul uano s!aoeds sisaynodKy ay1 Jano Sulwwns uonewrxoIdde dVW
ximation appro MAP intractable often is space othesis hyp the over Summing attributes) 6 of functions olean Bo 18,446,744,073,709,551,616 (e.g., ) d|i h( P maximizing MAP h ose cho rning: lea (MAP) ri osterio p a Maximum h| d( P maximize I.e., r o )i h( P)i )i h( P log +)i h| d( P log ) of (negative as ed view eb can terms Log othesis hyp de enco to bits + othesis hyp given data de enco to bits rning lea (MDL) length description minimum of idea basic the is This otherwise 0 consistent, if 1 is )i h| d( P otheses, hyp deterministic r oF science) (cf. othesis hyp consistent simplest = MAP ⇒ 7 1–3 Sections 20, Chapter

88-1suo139S0元pdgD poynaw Bulujeal leonsnens (uelsaKeg-uou)puepuens,,ay1 s!TW (Axa]dwo awes ayi go aue sasaynodKy lle j!a]qeuoseal s!yolym) 1 oud woj!un od∀Wo4IeI4up!:eepy4o4y153q∂y418 Kjdwis“3'1 (p)d Buizlwixew Tivy asooyp :uueal (W)pooy!lax!l wnwixew quenaauu sawooaq joud 'sias enep agel oy uorgewrxodde I
ximation appro ML irrelevant ecomes b r rio p sets, data rge la r oF )i h| d( P maximizing ML h ose cho rning: lea (ML) do eliho lik Maximum r rio p rm unifo r fo MAP to identical data; the to fit est b the get simply I.e., y) complexit same the of re a otheses hyp all if reasonable is (which d metho rning lea statistical esian) y (non-Ba rd” “standa the is ML 8 1–3 Sections 20, Chapter

6 8-I suonoos'0 isiunoo 0 yIM swajqoud sasneo inq 'ajqisuas swaas N_1+2=0 ← 0=9-I-0= OP 0 ()Tp I= (0-1)+=(oulpdo=(ulp)d o=(ulp)T :pooy!lay!l-o1 ay1 oj aisea s!yolym-0''M sIyl aziwixeW ,0-t)·0=(ylp)dⅡ=(ulp)d os 'suonenasqo (painqunsip Klleonuap!'quapuadapul)'p'l'!aue asayL sau!l 2-N-pue salayp 2 'salpueo N deumun am asoddns 0ADIH sjapow jo Klwej (jelwoulq)ajdwls siya joj jaaweed e s! 0 0y sasayiodKy jo wnnunuo :a]qissod s!Auy (a4=)d iselpue Kuay jo uonpey :Jaunpejnuew Mau e wolj geg sqou saKeg ur Suruleol ogaweled II
nets es y Ba in learning parameter ML candies? cherry of θ fraction manufacturer; new a from Bag Flavor ) F=cherry ( P θ θ h otheses hyp of continuum ossible: p is θ Any dels mo of family ) binomial ( simple this r fo rameter pa a is θ limes c − N=` and cherries c candies, N unwrap e w ose Supp so observations, distributed) identically endent, (indep i.i.d. re a These =)θ h| d( P NY1 =j θ =)θ h|j d( P c ) θ − (1 · ` : do eliho log-lik the r fo easier is —which θ w.r.t. this Maximize =)θ h| d( P log =)θ h| d( L NX1 =j ) θ − (1 log ` +θ log c =)θ h|j d( P log )θ h| d( dL dθ = c θ − ` θ −1 =θ ⇒ 0 = c ` +c = cN counts! 0 with roblems p causes but sensible, Seems 9 1–3 Sections 20, Chapter

01-1so1ps‘0 ideo [(0-L)8oI6+08or0d]+ [(0-L)8or6+08or.d+ [(0-I)8or7+080】=7 6(0-I),0·6(0-I)0·,(0-I)0=(9094lp)d addD!M :13‘selpueo Kuayp paddem-p3,l‘salpue N ‘0 awy (0-)·0= 0 6f4a43 (9904‘34p=Hu3au6=M)d(9g04u34p=H)d= (Pa=M)d (00o u2al6=MfLay=dd JOADI :addem uaa8u!Kpue人uayp,83‘io]pooy!ay!门 0 (xuay5=d)d oey uo Alleons!qeqoud spuadep addeM u/pay sIozaweed ald:aInA
parameters Multiple ) F=cherry ( P r: flavo on robabilistically p ends dep er wrapp Red/green Flavor Wrapper ) F | W=red ( P F cherry 2 θ lime 1 θ θ er: wrapp green in candy cherry e.g., r, fo do eliho Lik )2 ,θ 1 ,θ θ h| en e gr = W, cherry = F( P )2 ,θ 1 ,θ θ h, cherry = F| en e gr = W( P)2 ,θ 1 ,θ θ h| cherry = F( P = )1 θ − (1 · θ = etc.: candies, cherry ed red-wrapp c r candies, N θ =)2 ,θ 1 ,θ θ h| d( P c ) θ − (1 ` θ· cr1 )1 θ − (1 c g θ· r` 2 )2 θ − (1 g` )] θ − (1 log ` +θ log c[ = L )] 1 θ − (1 log c g +1 θ log c r[ + )] 2 θ − (1 log ` g +2 θ log ` r[ + 10 1–3 Sections 20, Chapter