
【g-1som9 S'gI dD G-I SNOILOS GI HLdVHO STH(OW ALITavaoud IvHOdNL
models obability pr Temporal 1–5 Sections 15, Chapter 1 1–5 Sections 15, Chapter

8uuB4y1pIμed◇ syJomiau uelsaKeg olweu (uonuaw jauq e)saily uewjey sjapow noyeW uapp!H◇ 8uI叫1 oous 'uo14pIp3d‘8uμg3uul◇ K4uIeμ3 un pue3wuIL◇ ourino
Outline y uncertaint and Time ♦ othing smo rediction, p filtering, Inference: ♦ dels mo ov rk Ma Hidden ♦ mention) rief b (a filters Kalman ♦ rks ow net esian y Ba Dynamic ♦ filtering rticle aP ♦ 2 1–5 Sections 15, Chapter

g-I suopos'gI dodeyo X1-X+XX=X :uoneoN wajqod uo spuadap azis dans :owrg azaosIp sounsse siyL ayDTpooHyasmd 6nSpoolgpa.msvaw 7 awn ie sajqeuen aouapina ajqenjasqo jo 1as 14squaquoDyoDwois 6nSpoolg 2 awn ie sajqeuen alens ajqenasqoun jo 1as =X dans awn ypea joy sajqeuen aouapIna pue anens Adoo eap!oiseg sisougelp applyan sA quawageuew seneqel 1!1paud pue yoen on paau am :segueyp plom ay_ Aqureglooun pue ow!L
yt uncertain and Time it redict p and track to need e w changes; rld ow The diagnosis vehicle vs management etes Diab step time each r fo riables va evidence and state y cop idea: Basic t time at riables va state unobservable of set =t X ar ug oodS l B e.g., t ontents tomachC S, t etc. , t time at riables va evidence observable of set =t E ar ug oodS l edB easur M e.g., t ate seR ul P, t aten oodE F, t roblem p on ends dep size step ; time discrete assumes This a X Notation: a X =b: X, . . . , +1 a X, 1 −b X, b 3 1–5 Sections 15, Chapter
pg-I suonoos'gt e oy paxy (XHd lapow josuas pue (T-XX)d pow uonsue :ssaood Keuones (d=()d :uondwnsse Aoyew Josuas +4 -1 lepJo-puooas 乙+1 1 JapJo-1sJl (I-X-)d=(1-10xX)d:ssaood noyeW Japo-puoas (1-XX)d=(IXx)d :ssaood AoxeW Jpo-1s! I-F0X Jo 1asqns papunoq uo spuadap 'X :uondunsse Aoyew isquaed :selqeuen asay woyj au saKeg e ansuo) surey5 AoyIe) sossoood AoyIeI
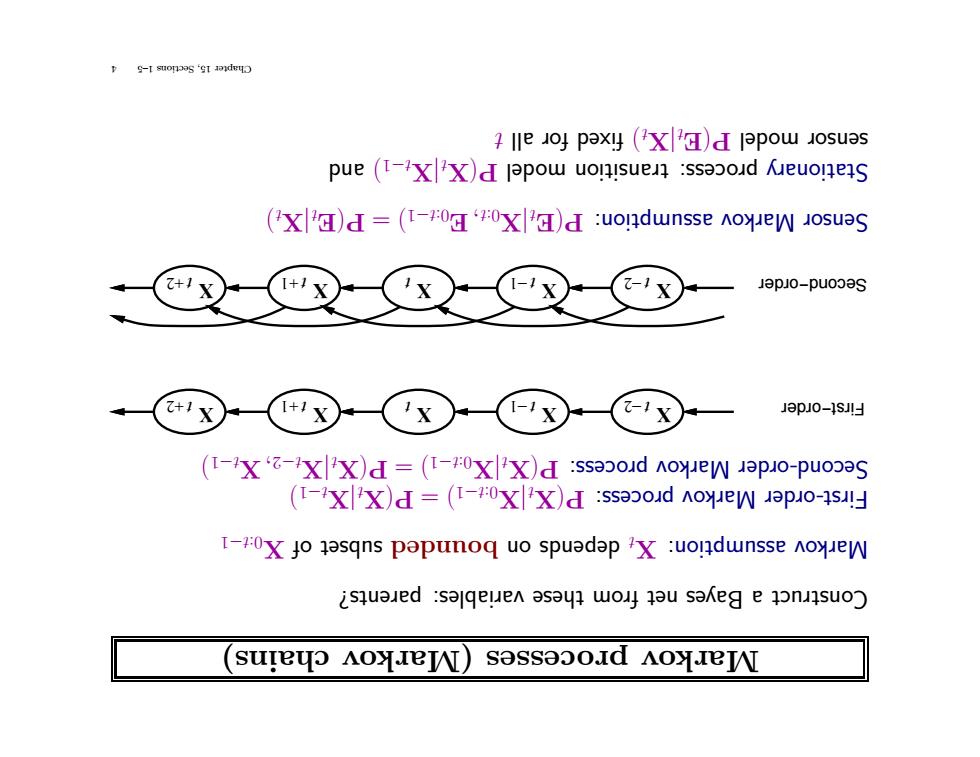
hains) c vo (Mark cesses pro vo Mark rents? pa riables: va these from net es y Ba a Construct 1 −t 0: X of subset ounded b on ends dep t X: assumption ov rk Ma )1 −t X|t X( P =)1 −t 0: X|t X( P: cess ro p ov rk Ma rder First-o )1 −t X, 2 −t X|t X( P =)1 −t 0: X|t X( P: cess ro p ov rk Ma rder Second-o +2 t X +1 t X t X −1 t X −2 t X +2 t X +1 t X t X −1 t X −2 t X First−order Second−order )t X|t E( P =)1 −t 0: E,t 0: X|t E( P: assumption ov rk Ma r Senso and )1 −t X|t X( P del mo transition cess: ro p ry Stationa t all r fo fixed )t X|t E( P del mo r senso 4 1–5 Sections 15, Chapter
g9-I suonos'gI todo f.ang yIM Ao pue uonsod quaw3ny uo14 ou noqo.13 dwex妇 lauinssa.ld "dua I ppe "3a 'anens quowsny 't ssaood Aoyuew Jo op.Io asea.IouI' s3X刈∂9Iss0d ipJom lea u!an Kpexe nou uondwnsse noyueW Japo-1s!y 1+1p1a1qu2 pllaiqwn 1-1pmaxqwn 0 (n)d +luind uind 1-luid L01 (Wd 1-4 odwexH
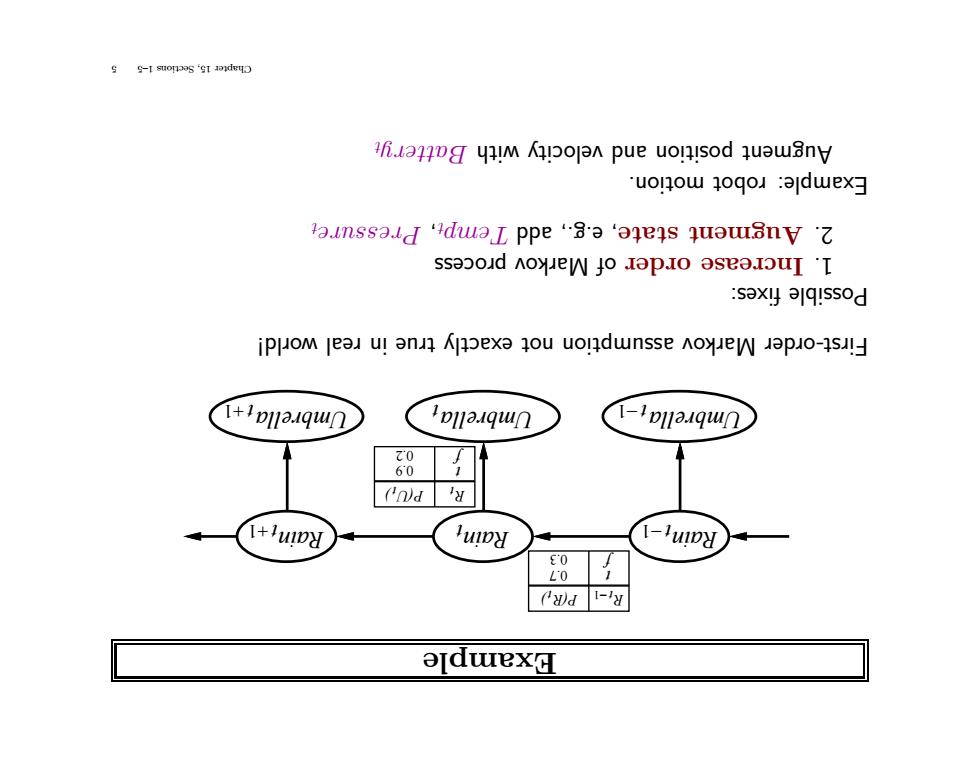
Example t Rain t Umbrella Rain −1 t Umbrella −1 t Rain +1 t Umbrella +1 t t P(R ) −1 t R 0.3 f 0.7 t t P(U ) t R 0.9 t 0.2 f rld! ow real in true exactly not assumption ov rk Ma rder First-o fixes: ossible P cess ro p ov rk Ma of order Increase 1. emp T add e.g., , state t Augmen 2. t e essur r P, t motion. ot rob Example: t y atter B with y cit velo and osition p Augment 5 1–5 Sections 15, Chapter

9 g-I suonoos'gt lauueyp Ksiou e yiIM Sulpooap 'uollugoa ypaads (xxxee:uoneueldx!soW Sulujeal oj jenuassa 'sanens ised jo anewnsa janaq >00 ()d :Bulyoows aouapIna ay1 inoy Im gualyay!l :saouanbas uonpe ajqissod jo uolenjene 0<y0 (x)d :uonp!pald quage jeuone e yo ssaood uoisipap ayn on indul-anes jaljaq (oX)d:auua」 syse aouelojul
tasks Inference )t 1: e|t X( P: Filtering agent rational a of cess ro p decision the to —input state elief b 0 >kr fo )t 1: e| k +t X( P: Prediction sequences; action ossible p of evaluation evidence the without filtering e lik t <k ≤0 r fo )t 1: e| k X( P: othing Smo rning lea r fo essential states, past of estimate etter b x max arg : explanation ely lik Most Pt 1: )t 1: e|t 1: x( channel noisy a with ding deco recognition, eech sp 6 1–5 Sections 15, Chapter

L g-I suopos'gI dodeyo go quapuadepu!)queasuoo aeds pue aw!L ()d=]yM (1+J)CHVMHO=1+] (Fx)d(x 1+X)dx(1+Xta)do (1ax)d(a4x+X)dx☒(+X1+约)do=(+a|+X)d :X ino Bulwwns Kq uonpipald 'uonewnsa uonplpaud"' (F1+x)d(1+X|+)do (6|I+X)d(6T+X|+)do= (1++X)d=(1++x)d ((x)d'+)f=(1++x)d u叫Iμo31euoI1euIs331 ens aArs.In0a,Ie3s1 ap :wly uIO!H
Filtering rithm: algo estimation state e recursiv a devise Aim: )) t 1: e|t X( P, +1 t e( f =) +1 t 1: e| +1 t X( P ) +1 t e,t 1: e| +1 t X( P =) +1 t 1: e| +1 t X( P )t 1: e| +1 t X( P)t 1: e, +1 t X| +1 t e( Pα = )t 1: e| +1 t X( P) +1 t X| +1 t e( Pα = X out summing yb Prediction . estimation + rediction p I.e., t: )t 1: e|t x( P)t 1: e,t x| +1 t X( Pt x Σ) +1 t X| +1 t e( Pα =) +1 t 1: e| +1 t X( P )t 1: e|t x( P)t x| +1 t X( Pt x Σ) +1 t X| +1 t e( Pα = )t 1: e|t X( P=t 1: f where ) +1 t e,t 1: f( ard w or F = +1 t 1: f )t of endent (indep t constan space and Time 7 1–5 Sections 15, Chapter
8 g-I suonoos'gt ℃p11a.qun Ipllaiqun 乙u1DH luiy Ouiy LLLO Z8L0 0090 3se」 e88^0 8L8^0 0090 anJL 、 ELE0 0090。 LZ9^0 0090 odwexo 3uI1!H
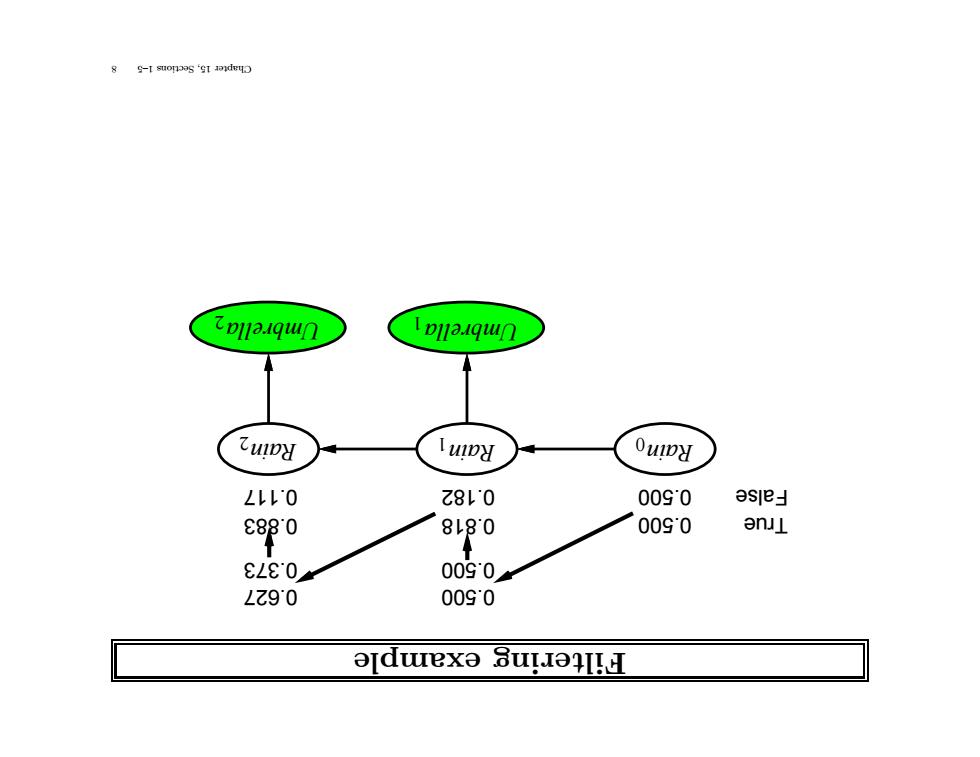
example Filtering Rain1 Umbrella1 Rain2 Umbrella2 Rain0 0.818 0.182 0.627 0.373 0.883 0.117 True False 0.500 0.500 0.500 0.500 8 1–5 Sections 15, Chapter

6S-1so19S‘gT4dw3 (X+x)d(+x+)d(1+xI+)d= (X+x)d(+x+d= (Xx)d(1+xX)d=(X+)d uolsuna spiemypeq e Kq paindwoo agessew puemypeg EI+YqYIJO (X|1+)d(x)do (X+)d(x)do= (T+治wolX)d=(oYX)d :1:1+Ya:Ta oul FTa aouapina pIA! Suryloows
othing Smo 1 X 0 X t E k E 1 E t X k X :t +1: k e, k 1: e into t 1: e evidence Divide )t +1: k e, k 1: e| k X( P =)t 1: e| k X( P )k 1: e, k X|t +1: k e( P)k 1: e| k X( Pα = )k X|t +1: k e( P)k 1: e| k X( Pα = t +1: k bk 1: f α = recursion: rds a backw a yb computed message rd a Backw )k X| +1 k x( P) +1 k x, k X|t +1: k e( P+1 k x Σ =)k X|t +1: k e( P )k X| +1 k x( P) +1 k x|t +1: k e( P +1 k x Σ = )k X| +1 k x( P) +1 k x|t +2: k e( P) +1 k x| +1 k e( P +1 k x Σ = 9 1–5 Sections 15, Chapter
(J2)Oeds‘(uu!3Kod)?u!eu川uL Kem ay1 Buoje saBessaw puemuoy aypeo wynloe piemypeq-puemoy 乙112.qun Ipllaqun 乙u1DH luny OuIy piemyoeq 0001 0L0 0001 0690 payoows ∠↓0 LLL'O e880 8880 pieMoy LLL'O Z8L0 0090 asjey c880 8L80 0090 ELE0 0090 LZ901 0090 alduexa
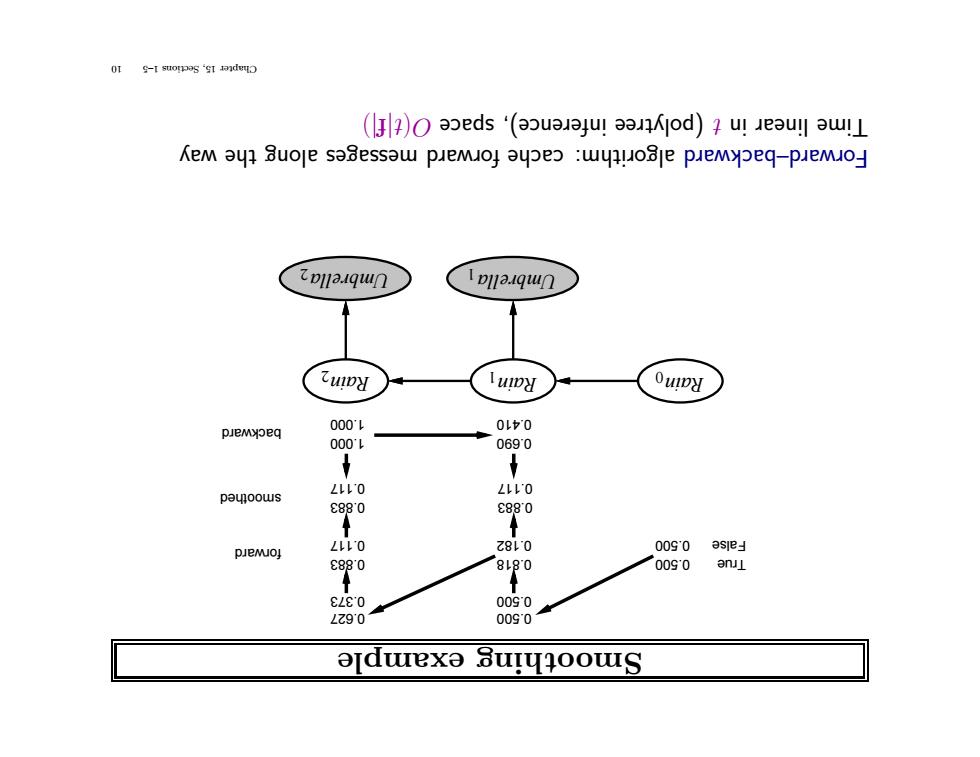
example othing Smo Rain1 Umbrella1 Rain2 Umbrella2 Rain0 True False 0.818 0.182 0.627 0.373 0.883 0.117 0.500 0.500 0.500 0.500 1.000 1.000 0.690 0.410 0.883 0.117 forward backward smoothed 0.883 0.117 ya w the along messages rd a rw fo cache rithm: algo rd a rd–backw a rwoF )|f|t( O space inference), olytree (p t in r linea Time 10 1–5 Sections 15, Chapter