
Manipulators ROBOTICS CHAPTER 25 C( umbers 6is the minimum number required to position end-effector arbitrarily. For dynamical systems,add velocity for each DOF. Outline Non-holonomic robots Robots,Effectors,and Sensors Localization and Mapping Motion Planning Motor Control annot generally transitio Mobile Robots Sensors nts wheels).inertials force sensors,torque sensors
Robotics Chapter 25 Chapter 25 1 Outline Robots, Effectors, and Sensors Localization and Mapping Motion Planning Motor Control Chapter 25 2 Mobile Robots Chapter 25 3 Manipulators R R R P R R Configuration of robot specified by 6 numbers ⇒ 6 degrees of freedom (DOF) 6 is the minimum number required to position end-effector arbitrarily. For dynamical systems, add velocity for each DOF. Chapter 25 4 Non-holonomic robots θ (x, y) A car has more DOF (3) than controls (2), so is non-holonomic; cannot generally transition between two infinitesimally close configurations Chapter 25 5 Sensors Range finders: sonar (land, underwater), laser range finder, radar (aircraft), tactile sensors, GPS Imaging sensors: cameras (visual, infrared) Proprioceptive sensors: shaft decoders (joints, wheels), inertial sensors, force sensors, torque sensors Chapter 25 6

Localization-Where am I? Localization contd. Compute cu rrent location ando(ivbrations Canausextended Kalmanfilter or simple cases: -40009e0 Localization contd Mapping SLAM:given observed landmarks,update pose and map distribution Probabilistic formulation of SLAM- to the state vector Localization contd. Mapping contd. 57囊 回而
Localization—Where Am I? Compute current location and orientation (pose) given observations: Xt Xt+1 At−2 At−1 At Zt−1 Xt−1 Zt Zt+1 Chapter 25 7 Localization contd. xi, yi vt ∆t t ∆t t+1 xt+1 h(xt ) xt θt θ ω Z1 Z2 Z3 Z4 Assume Gaussian noise in motion prediction, sensor range measurements Chapter 25 8 Localization contd. Can use particle filtering to produce approximate position estimate Robot position Robot position Robot position Chapter 25 9 Localization contd. Can also use extended Kalman filter for simple cases: robot landmark Assumes that landmarks are identifiable—otherwise, posterior is multimodal Chapter 25 10 Mapping Localization: given map and observed landmarks, update pose distribution Mapping: given pose and observed landmarks, update map distribution SLAM: given observed landmarks, update pose and map distribution Probabilistic formulation of SLAM: add landmark locations L1, . . . , Lk to the state vector, proceed as for localization Chapter 25 11 Mapping contd. Chapter 25 12

3D Mapping example Cell decomposition example Motion Planning Skeletonization:Voronoi diagram plan in configuratio space define y th ot's DOF Problem:doesn'ale well to Configuration space planning Skeletonization:Probabilistic Roadmap Basic problem:states!Convert to finite state space
3D Mapping example Chapter 25 13 Motion Planning Idea: plan in configuration space defined by the robot’s DOFs conf-3 conf-1 conf-2 conf-3 conf-2 conf-1 w w elb shou Solution is a point trajectory in free C-space Chapter 25 14 Configuration space planning Basic problem: ∞d states! Convert to finite state space. Cell decomposition: divide up space into simple cells, each of which can be traversed “easily” (e.g., convex) Skeletonization: identify finite number of easily connected points/lines that form a graph such that any two points are connected by a path on the graph Chapter 25 15 Cell decomposition example start goal start goal Problem: may be no path in pure freespace cells Solution: recursive decomposition of mixed (free+obstacle) cells Chapter 25 16 Skeletonization: Voronoi diagram Voronoi diagram: locus of points equidistant from obstacles Problem: doesn’t scale well to higher dimensions Chapter 25 17 Skeletonization: Probabilistic Roadmap A probabilistic roadmap is generated by generating random points in C-space and keeping those in freespace; create graph by joining pairs by straight lines Problem: need to generate enough points to ensure that every start/goal pair is connected through the graph Chapter 25 18

Motor control Simple learning algorithm:Stochastic gradient Minimize Eby gradient descent 0ercaeeckmat Given samples ().j=1.....N.we haw drd Biological motor control What the algorithm is doing Motor control systems are characterized by massive redundanc XX ldea:if the arm is noisy.only "one"optimal policy minimizes error at target no-toerancemightmotor behaviour Setup Results for 2-D controller Output (distance from target)F(0) ● 004
Motor control Can view the motor control problem as a search problem in the dynamic rather than kinematic state space: – state space defined by x1, x2, . . . , x˙1, x˙2, . . . – continuous, high-dimensional (Sarcos humanoid: 162 dimensions) Deterministic control: many problems are exactly solvable esp. if linear, low-dimensional, exactly known, observable Simple regulatory control laws are effective for specified motions Stochastic optimal control: very few problems exactly solvable ⇒ approximate/adaptive methods Chapter 25 19 Biological motor control Motor control systems are characterized by massive redundancy Infinitely many trajectories achieve any given task E.g., 3-link arm moving in plane throwing at a target simple 12-parameter controller, one degree of freedom at target 11-dimensional continuous space of optimal controllers Idea: if the arm is noisy, only “one” optimal policy minimizes error at target I.e., noise-tolerance might explain actual motor behaviour Harris & Wolpert (Nature, 1998): signal-dependent noise explains eye saccade velocity profile perfectly Chapter 25 20 Setup Suppose a controller has “intended” control parameters θ0 which are corrupted by noise, giving θ drawn from Pθ0 Output (e.g., distance from target) y = F(θ); y Chapter 25 21 Simple learning algorithm: Stochastic gradient Minimize Eθ[y 2 ] by gradient descent: ∇θ0Eθ[y 2 ] = ∇θ0 Z Pθ0 (θ)F(θ) 2 dθ = Z ∇θ0Pθ0 (θ) Pθ0 (θ) F(θ) 2Pθ0 (θ)dθ = Eθ[ ∇θ0Pθ0 (θ) Pθ0 (θ) y 2 ] Given samples (θj , yj), j = 1, . . . , N, we have ∇ ˆ θ0Eθ[y 2 ] = 1 N XN j=1 ∇θ0Pθ0 (θj) Pθ0 (θj) y 2 j For Gaussian noise with covariance Σ, i.e., Pθ0 (θ) = N(θ0,Σ), we obtain ∇ ˆ θ0Eθ[y 2 ] = 1 N XN j=1 Σ −1 (θj − θ0)y 2 j Chapter 25 22 What the algorithm is doing x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x Chapter 25 23 Results for 2–D controller 4 5 6 7 8 9 10 0.2 0.4 0.6 0.8 1 1.2 Velocity v Angle phi Chapter 25 24
Results for 2-D controller 06 Results for 2-D controller 0075 Summary The rubber hits the road Mobile robots and manipulators mh
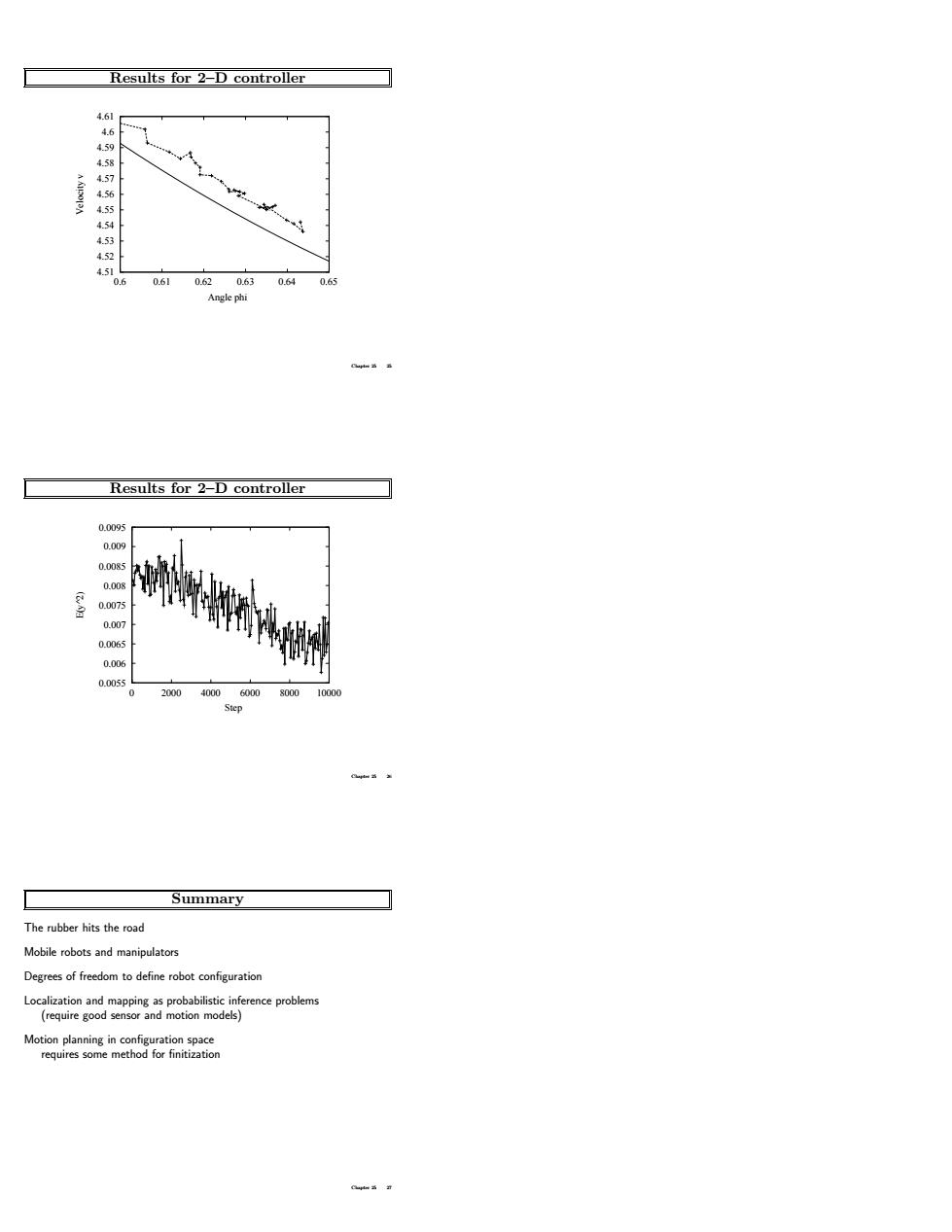
Results for 2–D controller 4.51 4.52 4.53 4.54 4.55 4.56 4.57 4.58 4.59 4.6 4.61 0.6 0.61 0.62 0.63 0.64 0.65 Velocity v Angle phi Chapter 25 25 Results for 2–D controller 0.0055 0.006 0.0065 0.007 0.0075 0.008 0.0085 0.009 0.0095 0 2000 4000 6000 8000 10000 E(y^2) Step Chapter 25 26 Summary The rubber hits the road Mobile robots and manipulators Degrees of freedom to define robot configuration Localization and mapping as probabilistic inference problems (require good sensor and motion models) Motion planning in configuration space requires some method for finitization Chapter 25 27