
Game Playing 吉建民 USTC jianminOustc.edu.cn 2022年3月28日 口◆4日1三1,是90C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Game Playing 吉建民 USTC jianmin@ustc.edu.cn 2022 年 3 月 28 日

Used Materials Disclaimer:本课件采用了S.Russell and P.Norvig's Artificial Intelligence-A modern approach slides,徐林莉老师课件和其他网 络课程课件,也采用了GitHub中开源代码,以及部分网络博客 内容 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Used Materials Disclaimer: 本课件采用了 S. Russell and P. Norvig’s Artificial Intelligence –A modern approach slides, 徐林莉老师课件和其他网 络课程课件,也采用了 GitHub 中开源代码,以及部分网络博客 内容

Table of Contents Games Perfect play(最优策略 minimax decisions a-B Pruning Resource limits and approximate evaluation Games of chance(包含几率因素的游戏 Games of imperfect information 4口◆464三+1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Table of Contents Games Perfect play(最优策略) minimax decisions α − β Pruning Resource limits and approximate evaluation Games of chance (包含几率因素的游戏) Games of imperfect information

Game Playing Game playing was thought to be a good problem for Al research: game playing is non-trivial ~Perfect play(最优策略) ,players need“human--like”intelligence games can be very complex (e.g.,Chess,Go) requires decision making within limited time games usually are: well-defined and repeatable fully observable and limited environments can directly compare humans and computers 口卡·三4色,是分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Game Playing Game playing was thought to be a good problem for AI research: ▶ game playing is non-trivial ▶ Perfect play(最优策略) ▶ players need “human-like”intelligence ▶ games can be very complex (e.g., Chess, Go) ▶ requires decision making within limited time ▶ games usually are: ▶ well-defined and repeatable ▶ fully observable and limited environments ▶ can directly compare humans and computers

Computers Playing Chess 4口卡404三·1=生0C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Computers Playing Chess

Computers Playing Go KBA Google DeepMind o:AlphaGo Challenge Match 口·三4,进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Computers Playing Go

Games vs.search problems “Unpredictable”opponent(不可预测的对手)→solution is a strategy specifying a move for every possible opponent reply Time limits=unlikely to find goal,must approximate 游戏对于低效率有严厉的惩罚 Plan of attack: Computer considers possible lines of play (Babbage,1846) Algorithm for perfect play (Zermelo,1912;Von Neumann, 1944) Finite horizon,approximate evaluation(Zuse,1945;Wiener, 1948:Shannon,1950) First chess program(Turing,1951) Machine learning to improve evaluation accuracy (Samuel, 1952-57) Pruning (to allow deeper search(McCarthy,1956)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Games vs. search problems “Unpredictable”opponent(不可预测的对手)⇒ solution is a strategy specifying a move for every possible opponent reply Time limits ⇒ unlikely to find goal, must approximate 游戏对于低效率有严厉的惩罚 Plan of attack: ▶ Computer considers possible lines of play (Babbage, 1846) ▶ Algorithm for perfect play (Zermelo, 1912; Von Neumann, 1944) ▶ Finite horizon, approximate evaluation (Zuse, 1945; Wiener, 1948;Shannon, 1950) ▶ First chess program (Turing, 1951) ▶ Machine learning to improve evaluation accuracy (Samuel, 1952-57) ▶ Pruning(剪枝)to allow deeper search (McCarthy, 1956)
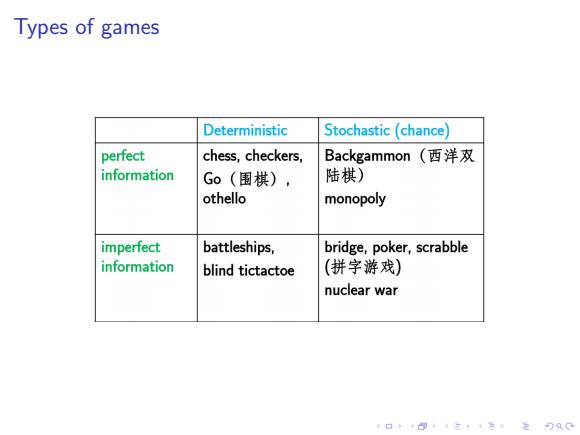
Types of games Deterministic Stochastic (chance perfect chess,checkers, Backgammon(西洋双 information G0(围棋), 陆棋) othello monopoly imperfect battleships, bridge,poker,scrabble information blind tictactoe (拼字游戏) nuclear war 口卡回·三4色是分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Types of games

Game Theory Models strategic interactions as games In normal-form games(matrix games),all players simultaneously select an action,and their joint action determines their individual payoff One-shot interaction Can be represented as an n-dimensional payoff matrix,for n players A player's strategy is defined as a probability distribution over his possible actions Stochastic games is an extension of normal-form games and MDPs in the sense that they deal with multiple agents in a multiple state situation. 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Game Theory ▶ Models strategic interactions as games ▶ In normal-form games (matrix games), all players simultaneously select an action, and their joint action determines their individual payoff ▶ One-shot interaction ▶ Can be represented as an n-dimensional payoff matrix, for n players ▶ A player’s strategy is defined as a probability distribution over his possible actions ▶ Stochastic games is an extension of normal-form games and MDPs in the sense that they deal with multiple agents in a multiple state situation

Normal-Form Game A normal-form game can be defined as a tuple (n,A1...n:R1..)where: n is the number of agents A;is the action set for player i A=A1 x...x An is the joint action set Ri:A-R is the reward function of player i Each agent i selects policyπi:Ai→[0,l刂(πi∈PD(A), takes action ai E A;with probability i(ai),and receives utility Ri(a1,...,an) Given policy profile(πi,,πn),expected utility to iis R(m1,....)=>R(a)IIm(aj) =1 Agents want to maximise their expected utilities 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Normal-Form Game ▶ A normal-form game can be defined as a tuple (n, A1...n, R1...n) where: ▶ n is the number of agents ▶ Ai is the action set for player i ▶ A = A1 × · · · × An is the joint action set ▶ Ri : A → R is the reward function of player i ▶ Each agent i selects policy πi : Ai → [0, 1] (πi ∈ PD(Ai)), takes action ai ∈ Ai with probability πi(ai), and receives utility Ri(a1, . . . , an) ▶ Given policy profile ⟨π1, . . . , πn⟩, expected utility to i is Ri(π1, . . . , πn) = ∑ a∈A Ri(a) ∏n j=1 πj(aj) ▶ Agents want to maximise their expected utilities