
Reinforcement Learning 吉建民 USTC jianminOustc.edu.cn 2021年6月11日 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Reinforcement Learning 吉建民 USTC jianmin@ustc.edu.cn 2021 年 6 月 11 日

Used Materials Disclaimer:本课件采用了Rich Sutton's RL class,David Silver's Deep RL tutorial和其他网络课程课件,也采用了GitHub中开源 代码,以及部分网络博客内容 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Used Materials Disclaimer: 本课件采用了 Rich Sutton’s RL class, David Silver’s Deep RL tutorial 和其他网络课程课件,也采用了 GitHub 中开源 代码,以及部分网络博客内容

Table of Contents 背景 MDPs 强化学习问题 蒙特卡洛方法(Monte Carlo Methods 蒙特卡洛预测(Monte Carlo Prediction) 蒙特卡洛控制(Monte Carlo Control) 时序差分学习(Temporal-Difference Learning 时序差分预测(TD Prediction 时序差分控制(TD Control) Sarsa:on-policy Q-learning off-policy 策略梯度(Policy Gradient Monte-Carlo Policy Gradient Actor-Critic Policy Gradient 深度强化学习 Deep Q-Networks (DQN) Policy Gradients for Deep Reinforcement Learning 4口卡404三·1=生0C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Table of Contents 背景 MDPs 强化学习问题 蒙特卡洛方法 (Monte Carlo Methods) 蒙特卡洛预测(Monte Carlo Prediction) 蒙特卡洛控制(Monte Carlo Control) 时序差分学习 (Temporal-Difference Learning) 时序差分预测(TD Prediction) 时序差分控制(TD Control) Sarsa:on-policy Q-learning : off-policy 策略梯度 (Policy Gradient) Monte-Carlo Policy Gradient Actor-Critic Policy Gradient 深度强化学习 Deep Q-Networks (DQN) Policy Gradients for Deep Reinforcement Learning

Markov Decision Processes MDP模型是一个四元组(S,A,T,R) Markov Property:P(s:+1 51,...,st)=P(st+1 st) ·Tsa,s)=P(s|s,a ~Policy:T:S×A→[0,1],T(a|s) ·已知MDP模型 ~Prediction::给定MDP和policy,计算值函数Vn或Qn -Control::给定MDP,计算最优策略π*或最优值函数V*或 Q* 019 0.4 05 06 人 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Markov Decision Processes ▶ MDP 模型是一个四元组 ⟨S, A,T, R⟩ ▶ Markov Property: P(st+1 | s1, . . . ,st) = P(st+1 | st) ▶ T(s, a,s ′ ) = P(s ′ | s, a) ▶ Policy: π : S × A → [0, 1], π(a | s) ▶ 已知 MDP 模型 ▶ Prediction: 给定 MDP 和 policy π,计算值函数 Vπ 或 Qπ ▶ Control: 给定 MDP,计算最优策略 π ∗ 或最优值函数 V ∗ 或 Q∗

State-Value Function and Action-Value Function ~回报(return):回报Gt是从时刻t开始的总折扣奖励: 00 G=R+1+R+2+…=∑)R+k1 k=1 ~状态值函数(state-value function):状态值函数V.(s是从 状态s出发,按照策略π采取行为得到的期望回报: Vx(s=Eπ(Gt|St=s) =E(Rt+1+7Gt+1St=s) =E(Rt+1+YV(St+1)ISt=s) 行动值函数(action-value function,action-state-value function):行为值函数Qπ(s,a)是从状态s出发,采取行为 a后,然后按照策略π采取行为得到的期望回报: Q(s,a)=E (Gt St=s,At=a) =ET(Rt+1+yQr(St+1,At+1)St=s,At=a) 4口卡404三·1怎生0C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . State-Value Function and Action-Value Function ▶ 回报(return):回报 Gt 是从时刻 t 开始的总折扣奖励: Gt = Rt+1 + γRt+2 + · · · = ∑∞ k=1 γ kRt+k+1 ▶ 状态值函数(state-value function):状态值函数 Vπ(s) 是从 状态 s 出发,按照策略 π 采取行为得到的期望回报: Vπ(s) = Eπ (Gt | St = s) = Eπ (Rt+1 + γGt+1 | St = s) = Eπ (Rt+1 + γVπ(St+1) | St = s) ▶ 行动值函数(action-value function, action-state-value function):行为值函数 Qπ(s, a) 是从状态 s 出发,采取行为 a 后,然后按照策略 π 采取行为得到的期望回报: Qπ(s, a) = Eπ (Gt | St = s, At = a) = Eπ (Rt+1 + γQπ(St+1, At+1) | St = s, At = a)
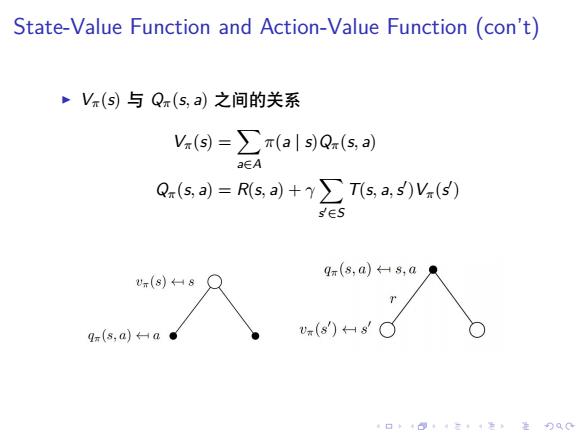
State-Value Function and Action-Value Function (con't) V(s)与Q(s,a)之间的关系 V.(s=∑π(als)Qx(s,a) aEA Q(s,a)=Rs,a)+∑Ts,a,s)V.(⑤) sES qr(s,a)8,a U(s)←Hs qm(s,a)←-a● u(s)HsC 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . State-Value Function and Action-Value Function (con’t) ▶ Vπ(s) 与 Qπ(s, a) 之间的关系 Vπ(s) = ∑ a∈A π(a | s)Qπ(s, a) Qπ(s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ )
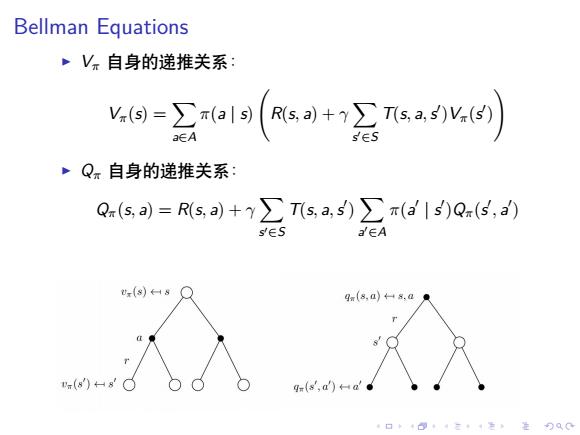
Bellman Equations ~Vπ自身的递推关系 -ga19(so+会sa网) a∈A ·Q。自身的递推关系: Q(s,)=Rs,a)+y∑Tsa,s)∑π(a'1s)Q(5,a) s∈S a∈A gm(8,a)8,a .(88 q(s,d)a 4口◆4⊙t4三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations ▶ Vπ 自身的递推关系: Vπ(s) = ∑ a∈A π(a | s) ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ ) ) ▶ Qπ 自身的递推关系: Qπ(s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ ) ∑ a ′∈A π(a ′ | s ′ )Qπ(s ′ , a ′ )

Bellman Equations(con't) ,最优状态值函数:最优值函数V(S)是在所有策略上的最大 值函数: V(s)=max V(s) 最优行为值函数:最优行为值函数Q*(s,a)是在所有策略上 的最大行为值函数 Q*(s,a)=max Q(s,a) V(s与Q*(s,a)之间的关系 V(s)=max V(s) =max∑x(als)Q.(s,a) aEA =max Q*(s,a) aEA 因为:MDP的optimal policy是deterministic policy,i.e, π*(S)=a 口◆4日1三1=,是90C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations (con’t) ▶ 最优状态值函数:最优值函数 V ∗ (s) 是在所有策略上的最大 值函数: V ∗ (s) = max π Vπ(s) ▶ 最优行为值函数:最优行为值函数 Q∗ (s, a) 是在所有策略上 的最大行为值函数 Q ∗ (s, a) = max π Qπ(s, a) ▶ V ∗ (s) 与 Q∗ (s, a) 之间的关系 V ∗ (s) = max π Vπ(s) = max π ∑ a∈A π(a | s)Qπ(s, a) = max a∈A Q ∗ (s, a) 因为:MDP 的 optimal policy 是 deterministic policy, i.e., π ∗ (s) = a

Bellman Equations(con't) V(s)与Q(s,a)之间的关系 Q*(s,a)=max Qr(s,a) =(风s+头sa) =Rs,a)+y∑Ts,a,s)V(s ·V(S)自身的递推关系 V(s)=max a∈A )+2.(4) E Q*(s,a)自身的递推关系 Q"(s,a)=R(s,a)+(s.a.5)mxs) a∈A sES
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations (con’t) ▶ V ∗ (s) 与 Q∗ (s, a) 之间的关系 Q ∗ (s, a) = max π Qπ(s, a) = max π ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ ) ) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )V ∗ (s ′ ) ▶ V ∗ (s) 自身的递推关系 V ∗ (s) = max a∈A ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )V ∗ (s ′ ) ) ▶ Q∗ (s, a) 自身的递推关系 Q ∗ (s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ ) max a ′∈A Q ∗ (s ′ , a ′ )

Dynamic Programming Algorithm Iterative Policy Evaluation Policy Iteration Value lteraton iHa○ n)。 8 Bellman Beliman Expectation Bellman Expectation Bellman Optimality E中uation Equation Equation Policy Iteration+ Equation Greedy Policy Improvement Problem Prediction Control Control 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Dynamic Programming