
NC&IS Link Analysis The CCF Advanced Disciplines Lectures 彭波 pb@net.pku.edu.cn 北京大学信息科学技术学院 6/27/2010
Link Analysis The CCF Advanced Disciplines Lectures 彭波 pb@net.pku.edu.cn 北京大学信息科学技术学院 6/27/2010
ANS I BBN/GTE CERFnet Ebone MCI Netcom Verlo

Web Graph Apple-Products SMC Ne 4 A ©2003 TouchGraph LLC http://www.touchgraph.com/TGGoogleBrowser.html
Web Graph http://www.touchgraph.com/TGGoogleBrowser.html
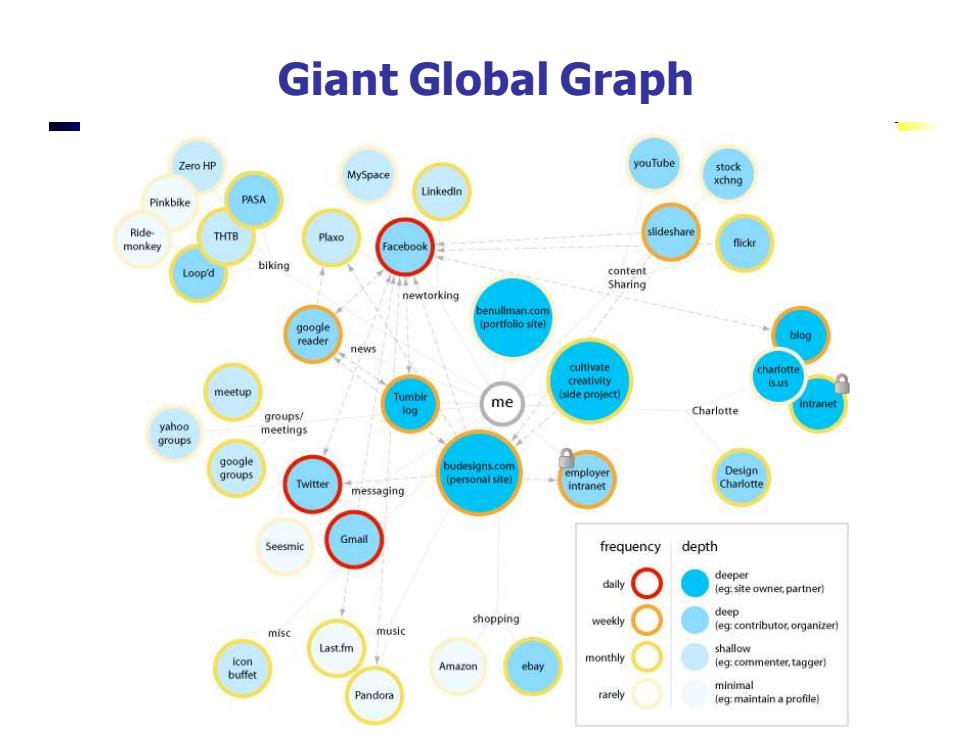
Giant Global Graph Zero HP stock MySpace xchng Pinkbike PASA Ride THTB monkey biking Loop'd content Sharing ng 9oogl (portiolio site) reader news cultivate creativity neetup side broject me gro Charlotte yahoo meetings Twitter messaging tran Charlotte Seesmic Gmail frequency depth deeper (eg:site owner.partner) shopping weekly deep (eg:contributor,organizer Last.fm shallow monthly Amazon ebay eg:commenter.tagger) minimal Pandora rarely (eg:maintain a profile】
Giant Global Graph

重要度的度量 刘翔 Paul Erdδs 一阶指标(“入度”) ·知晓关系:社会知名度 ·引用关系:认可程度 ● “高阶指标” ■和一个著名人物“共同发表”论文的“距离”:越短似 乎显得越“有荣誉”(例如,Erdos number,)
重要度的度量 ◼ 一阶指标(“入度”) ◼ 知晓关系:社会知名度 ◼ 引用关系:认可程度 ◼ “高阶指标” ◼ 和一个著名人物“共同发表”论文的“距离”:越短似 乎显得越“有荣誉”(例如,Erdos number,) 刘翔 Paul Erdös

对网页重要性的评价 PageRank算法,HITS(Hyperlink Induced Topic Search)算法 ■都是为了利用HTML网页的链接特 点,改善查询的效果 Larry Page Sergey Brin ,当Spam页面淹没了search enginel的 搜索结果页面时,除了页面内容与 查询的相关性以外,页面本身的质 量/重要性的作用就显现出来 Jon Kleinberg
对网页重要性的评价 ◼ PageRank算法,HITS(Hyperlink Induced Topic Search)算法 ◼ 都是为了利用HTML网页的链接特 点,改善查询的效果 ◼ 当Spam页面淹没了search engine的 搜索结果页面时,除了页面内容与 查询的相关性以外,页面本身的质 量/重要性的作用就显现出来 Larry Page & Sergey Brin Jon Kleinberg

PageRank B 34.3% 39 38.4% 8.1% Why and how it works? +d(PR(B) L(B) +0+)
PageRank Why and how it works?

谁重要一些? 如何用一个模型来刻画这种 感觉,使算出来的“重要性” 反映这种感觉? 0010 E= 1001 0100 认识甲的人可能和认识乙的人一样多,但认识乙的 人都是些“重要人物”,于是通常会认为乙比甲重 要 ■不仅是人,论文也是一样,被重要的文章引用的文 章可能就比较重要些
◼ 认识甲的人可能和认识乙的人一样多,但认识乙的 人都是些“重要人物”,于是通常会认为乙比甲重 要 ◼ 不仅是人,论文也是一样,被重要的文章引用的文 章可能就比较重要些 谁重要一些? 如何用一个模型来刻画这种 感觉,使算出来的“重要性” 反映这种感觉?

声望模型Reputation Model ■给定一个群体S,及其在上面的一个“知晓”关系 R,于是定义了一个有问“关系图”G。用邻接矩 阵E表示,E(,j)=1,当且仅当i听说过”j'(注意这 里没有程度之分,)。我们希望确定():所有个体 i∈S的“声望 模型=:p(=[k,k=1红n 即i在G上的 “入度”,亦即正的第列的1的个数 ·清楚、好计算;但是“不够好” 攀手晓盟人}望第k=1小,即的声望 ·清楚、显得要更“精确些”;但是,好计算吗?
声望模型Reputation Model ◼ 给定一个群体S,及其在上面的一个“知晓”关系 R,于是定义了一个有向“关系图”G。用邻接矩 阵E表示,E(i,j)=1,当且仅当i “听说过” j(注意这 里没有程度之分)。我们希望确定p(i):所有个体 i∈S的“声望” ◼ 模型一:p(i) = ∑E[k,i],k=1,…,n,即i在G上的 “入度”,亦即E的第i列的1的个数 ◼ 清楚、好计算;但是“不够好” ◼ 模型二:p(i) = ∑E[k,i]p(k),k=1,…,n,即i的声望 等于知晓他的人的声望之和 ◼ 清楚、显得要更“精确些” ;但是,好计算吗?

声望模型二 对于所有i,p()=∑E[k,i门p(k),k=1,,n 也就是,记p=(p(1),p(2),,p(n), p=Ep ■问题是: ■这个方程存在解吗? 般来讲:这 ·如果存在,如何得到? 个方程的非0解 ■如果不存在,该怎么办? 是不存在的!
声望模型二 ◼ 对于所有i,p(i) = ∑E[k,i]p(k),k=1,…,n ◼ 也就是,记p = (p(1), p(2), …, p(n))T , p = ETp ◼ 问题是: ◼ 这个方程存在解吗? ◼ 如果存在,如何得到? ◼ 如果不存在,该怎么办? 一般来讲:这 个方程的非0解 是不存在的!