中国科学技术大学：《数据结构及算法》课程教学资源（PPT课件讲稿）第2章 线性表

第2章线性表 2.1线性表的基本概念 2.2线性表的顺序表示 2.3线性表的链式表示 2.4线性结构的深入 ypb@ustc.edu.cn 中国科学技术大学

ypb@ustc.edu.cn 1 中国科学技术大学 第2章 线性表 2.1 线性表的基本概念 2.2 线性表的顺序表示 2.3线性表的链式表示 2.4线性结构的深入

2.1线性表的基本概念 ·线性表的定义 线性表是n(n>=O)个数据元素的有限序列，表中 各个元素具有相同地属性，表中相邻元素间存 在“序偶”关系。 记做：(a1,a2,…a-1a,a+1…,n-1,an） a1称为a的直接前驱元素，a+l是a的直接后继 元素 线性表的长度：表中的元素个数n 位序：称元素ai在线性表中的位序 ypb@ustc.edu.cn 中国科学技术大学

ypb@ustc.edu.cn 2 中国科学技术大学 2.1线性表的基本概念 • 线性表的定义 线性表是n(n>=0)个数据元素的有限序列，表中 各个元素具有相同地属性，表中相邻元素间存 在“序偶”关系。 记做：(a1 ,a2 ,…….ai-1 ,ai ,ai+1 ,…,an-1 ,an ) ai-1称为ai 的直接前驱元素，ai+1是ai的直接后继 元素 线性表的长度：表中的元素个数 n 位序：i称元素ai在线性表中的位序

S 线性表的基本操作 ADT List 数据对象：D={aa∈ElemSet,i=l,2,,n,n20} 数据结构：R={a-1,a>a-1,a1∈D,F2,3,, 基本操作： InitList(&L) Destroy(&L) ClearList(&L) ListEmpty(L) ListLength(L) GetElem(L,i,&e) 1<=i<=ListLength (L) LocateItem(L,e) PriorElem(L,Cur_e,&pre_e) NextElem(L,cur_e,&next_e) ListInsert(&L,i,e) 1<=i<=ListLength (L)+1 ListDelete(&L,i,&e) 1<=i长=ListLength(L) ListTraverse(L) End ADT List ypb@ustc.edu.cn 3 中国科学技术大学

ypb@ustc.edu.cn 3 中国科学技术大学 ADT List{ 数据对象:D={ ai |aiElemSet,i=1,2,…,n,n0} 数据结构:R={|ai-1 ,aiD,i=2,3,...,n} 基本操作： InitList(&L) Destroy(&L) ClearList(&L) ListEmpty(L) ListLength(L) GetElem(L,i,&e) 1<=i<= ListLength (L) LocateItem(L,e) PriorElem(L,Cur_e,&pre_e) NextElem(L,cur_e,&next_e) ListInsert(&L,i,e) 1<=i<= ListLength (L)+1 ListDelete(&L,i,&e) 1<=i<= ListLength (L) ListTraverse(L) }End ADT List 线性表的基本操作

【例】对两个线性表La、Lb表示的集合A和B,求一个 新集合A=AUB 算法2.1 > a)从Lb中取一个元素，并删除 b)在La中查询 c)若La中不存在，则将其插入La,重复直至Lb空 【例】对两个线性表La、Lb表示的集合A和B,求 A=A-B算法2.2☑ a)从Lb中取一个元素，并删除 b)在La中查询 c)若La中存在，则将从La删除，重复直至Lb空 3 ypb@ustc.edu.cn 中国科学技术大学

ypb@ustc.edu.cn 4 中国科学技术大学 【例】对两个线性表La、Lb表示的集合A和B，求一个 新集合A＝AUB 算法2.1 a) 从Lb中取一个元素，并删除 b) 在La中查询 c) 若La中不存在，则将其插入La，重复直至Lb空 【例】对两个线性表La、Lb表示的集合A和B ，求 A=A-B 算法2.2 a) 从Lb中取一个元素，并删除 b) 在La中查询 c) 若La中存在，则将从La删除，重复直至Lb空

2.2线性表的顺序表示 顺序表—线性表的顺序存储表示 Const LIST INIT SIZE=100: (C++规范) Const LISTINCREMENT=10: #define LIST INIT SIZE 100 (C规范) typedef struct{ Elemtype elem; int length; int listsize; int incrementsize: }SqList; ypb@ustc.edu.cn 5 中国科学技术大学

ypb@ustc.edu.cn 5 中国科学技术大学 2.2线性表的顺序表示 • 顺序表——线性表的顺序存储表示 Const LIST_INIT_SIZE=100; (C++规范) Const LISTINCREMENT=10; #define LIST_INIT_SIZE 100 (C规范) typedef struct { Elemtype * elem; int length; int listsize; int incrementsize; }SqList;

顺序表中基本操作的实现 初始化操作InitList Sq 算法2.3D 销毁操作DestroyList_Sq 算法2.4 是否为空ListEmpy_Sq 算法2.5D 是否满ListFull Sq 算法2.6 求长度ListLength_sq 算法2.7 查找元素操作LocateElem_Sq 算法2.8 获取元素操作GetItem Sq 算法2.9 插入元素操作ListInsert_Sq算法2.I0时间复杂度O(n) 删除元素操作ListDelete Sq算法2.I1时间复杂度O(n) 。 插入和删除操作的时间分析： Ein=>pi(n-i+1)=n/2 Edl=qi(n-i)=(n-1)/2 ypb@ustc.edu.cn 6 中国科学技术大学

ypb@ustc.edu.cn 6 中国科学技术大学 • 顺序表中基本操作的实现 初始化操作 InitList_Sq 算法2.3 销毁操作 DestroyList_Sq 算法2.4 是否为空 ListEmpy_Sq 算法2.5 是否满 ListFull_Sq 算法2.6 求长度 ListLength_sq 算法2.7 查找元素操作 LocateElem_Sq 算法2.8 获取元素操作 GetItem_Sq 算法2.9 插入元素操作 ListInsert_Sq 算法2.10 时间复杂度O(n) 删除元素操作 ListDelete_Sq 算法2.11时间复杂度O(n) • 插入和删除操作的时间分析： Ein=Σpi(n-i+1)=n/2 Edl=Σqi(n-i)=(n-1)/2

查找元素操作 算法2.8时间复杂度On) 例如：顺序表 L.elem L.listsize 23754138546217 L.length =7 e=38 返回值=4 e=50 返回值=0 ypb@ustc.edu.cn 中国科学技术大学

ypb@ustc.edu.cn 7 中国科学技术大学 查找元素操作 算法2.8 时间复杂度O(n) 例如：顺序表 23 75 41 38 54 62 17 L.elem L.length = 7 L.listsize e = 38 p p p p p i 12348 e = 50 p 返回值 = 4 返回值 = 0

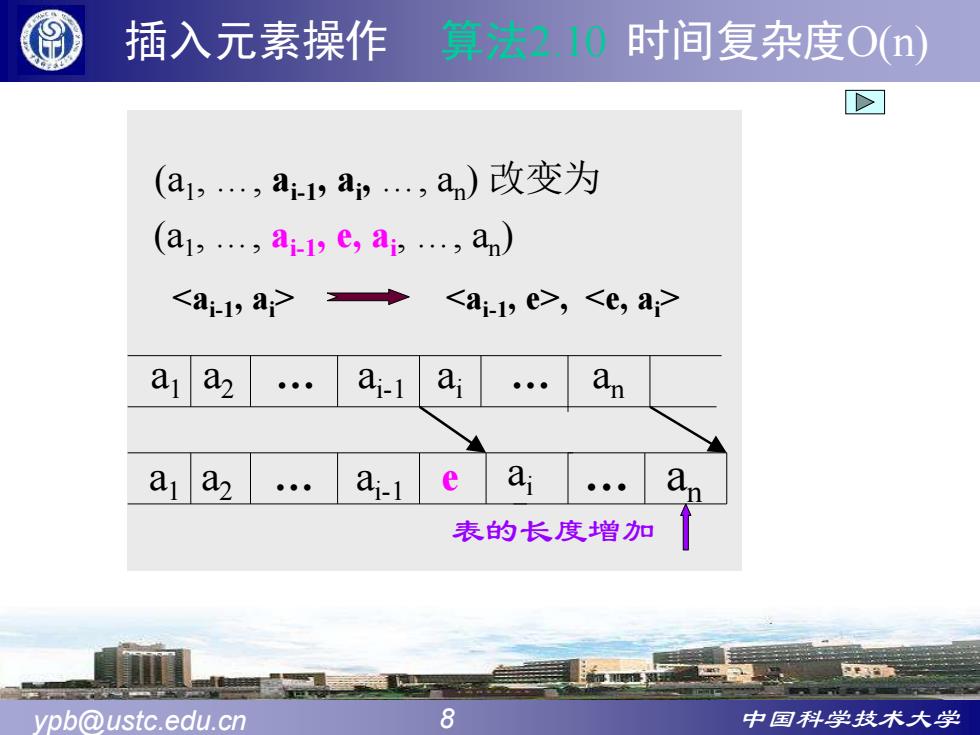
插入元素操作 算法2.10时间复杂度On) (a1,,a1,a,…,an)改变为 (a1,…,a-1ye,ab,an) ,<e,ap al a2 a-1 a a aa ai-1 e a a 表的长度增加 ypb@ustc.edu.cn 8 中国科学技术大学

ypb@ustc.edu.cn 8 中国科学技术大学 (a1 , …, ai-1 , ai , …, an ) 改变为 a1 a2 … ai-1 ai … an a1 a2 … ai-1 e ai … an , 表的长度增加 (a1 , …, ai-1 , e, ai , …, an ) 插入元素操作 算法2.10 时间复杂度O(n)

删除元素操作算法2,12时间复杂度On) >☒ (a1,…,a1,a,a+1,…,an)改变为 (a1,,a-wa+1,,an) ◆ <ai-p aitl a a ai-1 a at…am a 02 ai-1 aitl... An 表的长度减少 3 ypb@ustc.edu.cn 9 中国科学技术大学

ypb@ustc.edu.cn 9 中国科学技术大学 删除元素操作 算法2.12 时间复杂度O(n) (a1 , …, ai-1 , ai , ai+1, …, an ) 改变为 ai+1 … an , 表的长度减少 a1 a2 … ai-1 ai ai+1 … an a1 a2 … ai-1 (a1 , …, ai-1 , ai+1, …, an )

顺序表其它算法举例 例2.6用顺序表表示集合，完成例2.4。 算法2.13时间复杂度O(n2)>习 例2.10用尽量少得辅助空间将前m个元素和后n 个元素互换 -算法2.25 exchange1时间复杂度：O(m×n)> -算法2.26 invert时间复杂度：O(t-s+1)D -算法2.27 exchange2时间复杂度：O(m+n)☑ 23 ypb@ustc.edu.cn 10 中国科学技术大学

ypb@ustc.edu.cn 10 中国科学技术大学 例2.6 用顺序表表示集合，完成例2.4。 算法2.13 时间复杂度O(n2 ) 例2.10 用尽量少得辅助空间将前m个元素和后n 个元素互换 – 算法2.25 exchange1 时间复杂度：O(m×n) – 算法2.26 invert 时间复杂度：O(t-s+1) – 算法2.27 exchange2 时间复杂度：O(m+n) 顺序表其它算法举例