
《数据结构》习题集 第二章数据结构导论 思考题: 1.1简述下列术语:数据、数据元素、数据对象、数据结构、存储结构、数据 类型、抽象数据类型 作业题: 1.2设有数据结构(D,R),其中 D={d1,d2,d3,d4} R=(rl,r2) rl={,,,,,} r2={(d1,d2),(d1,d3),(d1,d4),(d2,d4),(d2,d3)} 试绘出其逻辑结构示意图。 1.3设n是正整数。试写出下列程序段中用记号“△”标注的语句的频度: (1)i=1;k=0: while(i<=n-1){ △k+=10*i: i+: (2)i=1;k=0: do △k+=10*i: i++: }while(i<=n-1) (3)i=1:k=0 do{ △k+=10*i:i+: }while(i==n); (4) 1=1:j0: while(i+j≤n){ △if(i<j)i+:else j++: 第1页
第 1 页 《数据结构》习题集 第二章 数据结构导论 思考题: 1.1 简述下列术 语:数据、数据元素、数据对象、数据结构、存储结构、数据 类型、抽象数据类型 作业题: 1.2 设有数据结构(D,R),其中 D={d1, d2, d3, d4 } R={r1, r2} r1={ , , , , , } r2={ (d1, d2), (d1, d3), (d1, d4), (d2, d4), (d2, d3) } 试绘出其逻辑结构示意图。 1.3 设 n 是正整数。试写出下列程序段中用记号“△”标注的语句的频度: (1) i=1; k=0; while(i<=n-1) { △ k+=10*i; i++; } (2) i=1; k=0; do { △ k+=10*i; i++; }while(i<=n-1) (3) i=1; k=0; do { △ k+ = 10*i; i++; }while(i==n); (4) i=1; j=0; while(i+j≤n) { △ if(i<j) i++; else j++; }

(⑤)x=n:y=0:/m是不小于1的常数 hi1e(x>=(y+1)*(y+1){ △y+ (6)x=91:y=100: while(y>0》 △if(x>100){x-=10:y-:} else x++; (7)for(i=0;i<n;i++) for(j=i;j<n:j++) for(k=j;k<n;k++) △x+=2: 第三章线性表 思考题: 2.1描述以下三个概念的区别:头指针、头结点、首元结点。 2.2描述以下几个概念:顺序存储结构、链式存储结构、顺序表、有序表。 作业题: 2.3已知顺序表La中数据元素按非递减有序排列。试写一个算法,将元素x插 到La的合适位置上,保持该表的有序性。 2.4己知单链表L中数据元素按非递减有序排列。按两种不同情况,分别写出 算法,将元素x插到La的合适位置上,保持该表的有序性:(l)La带头结点: (2)La不带头结点。 2.5试写一个算法,实现顺序表的就地逆置,即在原表的存储空间将线性表 (a,a,,ar,an)逆置为(a,a-,,a,a) 2.6试写一个算法,对带头结点的单链表实现就地逆置。 2.7己知线性表L采用顺序存储结构存放。对两种不同情况分别写出算法,删除 L中值相同的多余元素,使得L中没有重复元素:(1)L中数据元素无序排列:(②)L 第2页
第 2 页 (5) x=n; y=0; //n 是不小于 1 的常数 while(x>=(y+1)*(y+1)){ △ y++; } (6) x=91; y=100; while ( y>0 ) △ if(x>100) { x-=10; y--; } else x++ ; } (7) for( i=0; i<n; i++) for( j=i; j<n; j++) for( k=j; k<n; k++) △ x+=2; 第三章 线性表 思考题: 2.1 描述以下三个概念的区别:头指针、头结点、首元结点。 2.2 描述以下几个概念:顺序存储结构、链式存储结构、顺序表、有序表。 作业题: 2.3 已知顺序表 La 中数据元素按非递减有序排列。试写一个算法,将元素 x 插 到 La 的合适位置上,保持该表的有序性。 2.4 已知单链表 La 中数据元素按非递减有序排列。按两种不同情况,分别写出 算法,将元素 x 插到 La 的合适位置上,保持该表的有序性:(1)La 带头结点; (2)La 不带头结点。 2.5 试写一个算法,实现顺序表的就地逆置,即在原表的存储空间将线性表 (a1,a2, ..., an-1,an)逆置为(an,an-1, ..., a2,a1) 2.6 试写一个算法,对带头结点的单链表实现就地逆置。 2.7 已知线性表 L 采用顺序存储结构存放。对两种不同情况分别写出算法,删除 L 中值相同的多余元素,使得 L 中没有重复元素:(1)L 中数据元素无序排列;(2)L

中数据元素非递减有序排列。 2.8将2.7题中L的存储结构改为单链表,写出相应的实现算法。 2.9设有两个非递减有序的单链表A和B。请写出算法,将A和B“就地”归并 成一个按元素值非递增有序的单链表C。 2.10设有一个长度大于1的单向循环链表,表中既无头结点,也无头指针,s 为指向表中某个结点的指针,如图2-1所示。试编写一个算法,别除链表中指针 s所指结点的直接前驱。 待删结点3个 图2-1 2.11已知线性表用带头结点的单链表表示,表中结点由三类字符组成:字母、 数字和其他字符。试编写算法,将该线性链表分割成三个循环单链表,每个循环 单链表中均只含有一类字符。 2.12已知线性表用顺序存储结构表示,表中数据元素为个正整数。试写一算 法,分离该表中的奇数和偶数,使得所有奇数集中放在左侧,偶数集中放在右侧。 要求:(1)不借助辅助数组:(2)时间复杂度为0()。 2.13设以带头结点的双向循环链表表示的线性表L=(a,a,a,,a。试写 时间复杂度为0(m)的算法,将L改造为L=(a,as,,a,,a4,a)。 第四章栈和队列 思考题: 3.1简述栈和线性表的差别。 3.2如果进栈序列为A、B、C、D,写出所有可能的出栈序列。 3.3简述栈和队列的相同点和差异。 第3页
中数据元素非递减有序排列。 2.8 将 2.7 题中 L 的存储结构改为单链表,写出相应的实现算法。 2.9 设有两个非递减有序的单链表 A 和 B。请写出算法,将A和B“就地”归并 成一个按元素值非递增有序的单链表 C。 2.10 设有一个长度大于 1 的单向循环链表,表中既无头结点,也无头指针,s 为指向表中某个结点的指针,如图 2-1 所示。试编写一个算法,删除链表中指针 s 所指结点的直接前驱。 待删结点 s 图 2-1 2.11 已知线性表用带头结点的单链表表示,表中结点由三类字符组成:字母、 数字和其他字符。试编写算法,将该线性链表分割成三个循环单链表,每个循环 单链表中均只含有一类字符。 2.12 已知线性表用顺序存储结构表示,表中数据元素为 n 个正整数。试写一算 法,分离该表中的奇数和偶数,使得所有奇数集中放在左侧,偶数集中放在右侧。 要求:(1)不借助辅助数组;(2)时间复杂度为 O(n)。 2.13 设以带头结点的双向循环链表表示的线性表L=(a1,a2,a3,...,an)。试写一 时间复杂度为O(n)的算法,将L改造为L=(a1,a3,...,an,...,a4,a2)。 第四章 栈和队列 思考题: 3.1 简述栈和线性表的差别。 3.2 如果进栈序列为 A、B、C、D,写出所有可能的出栈序列。 3.3 简述栈和队列的相同点和差异。 第 3 页

3.4己知栈S中存放了8个数据元素,自栈底至栈顶依次为(1,2,3,4,5,6,7,8)。 (1)写出在执行了函数调用algol(S)后,S中的元素序列。 (2)在(1)的基础上,又执行了函数调用algo2(S,5),写出此时S中的元素 序列。 void algol(Stack &S){ int a[l0],i,n=0; while(!StackEmpty(S)){n++:Pop(S,a[n]): for(i=1;i<=n:i++)Push(S,a[i]) void algo2(Stack &S,int e){ Stack T: int d; InitStack(T): while(!EmptyStack(S)){ Pop(S,d); if(d!=e)Push(T,d); } while(!StackEmpty(T))( Pop(T,d); Push(S,d): 3.5已知队列Q中自队头至队尾依次存放者(1,2,3,4,5,6,7,8)。写出在执行了 函数调用algo3(Q)后,Q中的元素序列。 void algo3(Queue &Q) Stack S; int d; InitStack(S); while(!QueueEmpty(Q)){ 第4页
第 4 页 3.4 已知栈 S 中存放了 8 个数据元素,自栈底至栈顶依次为(1,2,3,4,5,6,7,8)。 (1)写出在执行了函数调用 algo1(S)后,S 中的元素序列。 (2)在(1)的基础上,又执行了函数调用 algo2(S,5),写出此时 S 中的元素 序列。 void algo1(Stack &S){ int a[10], i, n=0; while(!StackEmpty(S)){ n++; Pop(S, a[n]); } for(i=1; i<=n; i++) Push(S, a[i]); } void algo2(Stack &S, int e){ Stack T; int d; InitStack(T); while(!EmptyStack(S)){ Pop(S,d); if(d!=e) Push(T,d); } while(!StackEmpty(T)){ Pop(T,d); Push(S,d); } } 3.5 已知队列 Q 中自队头至队尾依次存放着(1,2,3,4,5,6,7,8)。写出在执行了 函数调用 algo3(Q)后,Q 中的元素序列。 void algo3(Queue &Q){ Stack S; int d; InitStack(S); while(!QueueEmpty(Q)){

DeQueue(Q,d):Push(S,d): while(!StackEmpty(S)){ Pop(S,d);EnQueue(Q,d); } 作业题: 3.6试写一个算法,识别依次读入的一个以@为结束符的字符序列是否为形如“序 列&序列2”模式的字符序列。其中,序列和序列中都不包含字符‘&',且序列 2是序列的逆序。例如,“a+bb+a”是属于该模式的字符序列,而“1+33一1” 则不是。 3.7假设一个算术表达式中可以包含三种符号:圆括号“(”和“)”、方括号“[” 和“门”、花括号“{”和“}”,且这三种括号可按任意次序嵌套使用。编写判别 给定表达式中所含的括号是否正确配对的算法(已知表达式已存入数据元素为字 符的顺序表中)。 3.8设表达式由单字母变量、双目运算符和圆括号组成(如:“(a*(b+c)-d)/e)”。 试写一个算法,将一个书写正确的表达式转换为逆波兰式。 3.9试用类C写一个算法,对逆波兰式求值。 3.10假设以带头结点的单循环链表表示队列,只设一个尾指针指向队尾元素, 不设头指针。试编写相应的队列初始化、入队和出队的算法。 3.11假设将循环队列定义为:以rear和length分别指示队尾元素和队列长度。 试给出此循环队列的队满条件,并写出相应的入队和出队算法(在出队算法中要 传递回队头元素的值)。 3.12试写一个算法:判别读入的一个以‘@'为结束符的字符序列是否是“回文” (所谓“回文”是指正读和反读都相同的字符序列,如“XXYZyXX”是回文,而 “abcab”则不是回文)。 第5页
第 5 页 DeQueue(Q,d); Push(S,d); } while(!StackEmpty(S)){ Pop(S,d); EnQueue(Q,d); } } 作业题: 3.6 试写一个算法,识别依次读入的一个以@为结束符的字符序列是否为形如“序 列1&序列2”模式的字符序列。其中,序列1和序列2中都不包含字符‘&’,且序列 2是序列1的逆序。例如,“a+b&b+a”是属于该模式的字符序列,而“1+3&3-1” 则不是。 3.7 假设一个算术表达式中可以包含三种符号:圆括号“(”和“)”、方括号“[” 和“]”、花括号“{”和“}”,且这三种括号可按任意次序嵌套使用。编写判别 给定表达式中所含的括号是否正确配对的算法(已知表达式已存入数据元素为字 符的顺序表中)。 3.8 设表达式由单字母变量、双目运算符和圆括号组成(如:“(a*(b+c)-d)/e)”。 试写一个算法,将一个书写正确的表达式转换为逆波兰式。 3.9 试用类 C 写一个算法,对逆波兰式求值。 3.10 假设以带头结点的单循环链表表示队列,只设一个尾指针指向队尾元素, 不设头指针。试编写相应的队列初始化、入队和出队的算法。 3.11 假设将循环队列定义为:以 rear 和 length 分别指示队尾元素和队列长度。 试给出此循环队列的队满条件,并写出相应的入队和出队算法(在出队算法中要 传递回队头元素的值)。 3.12 试写一个算法:判别读入的一个以‘@’为结束符的字符序列是否是“回文” (所谓“回文”是指正读和反读都相同的字符序列,如“xxyzyxx”是回文,而 “abcab”则不是回文)

第五章串和数组 5.1已知多维数组A[2][2][3][3]按行优先方式存储。试按存储位置的先后次 序,列出所有数组元素A[i][][k][1]序列(为了简化表达,可以只列出形如 “i,j,k,1”的序列,如元素A[0][0][2][1]可表示为“0,0,2,1”)。 5.2假设有一个二维数组A[0.5][0.7],每个元素占6个字节,首元素A[0][0] 的地址为1000,求: (1)A的体积: (2)最后一个元素A[5][7]的地址: (③)按行主序方式存储时,A[2][4]的地址: (4)按列主序方式存储时,A[2][4]的地址: 5.3设有上三角矩阵An×n, 0223. an 将其上三角的元素逐行存于数组B[0.m-l]中(m充分大),使得B[k]=且k= f(i)+f(j》+c。试推导出函数f1、f和常数c(要求f和f,中不含常数项)。 5.4设有一个准对角矩阵 aa a21422 a43a4 d2 d2m-2 22-42m2 按以下方式存于一维数组B[4如]中: 0123456 4m-24-1 a11 a12 821 a22 a33 a34 843...ajj...82a-1,2a 828.2a 第6页
第五章 串和数组 5.1 已知多维数组 A[2][2][3][3]按行优先方式存储。试按存储位置的先后次 序,列出所有数组元素 A[i][j][k][l]序列(为了简化表达,可以只列出形如 “i,j,k,l”的序列,如元素 A[0][0][2][1]可表示为“0,0,2,1” )。 5.2 假设有一个二维数组 A[0..5][0..7],每个元素占 6 个字节,首元素 A[0][0] 的地址为 1000,求: (1)A 的体积; (2)最后一个元素 A[5][7]的地址; (3)按行主序方式存储时,A[2][4]的地址; (4)按列主序方式存储时,A[2][4]的地址; 5.3 设有上三角矩阵 An×n, ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ nn n n n a C aa aaa aaaa ...... ... ... ... 33 3 2322 2 131211 1 将其上三角的元素逐行存于数组B[0..m-1]中(m充分大),使得B[k]=aij且k= f1(i)+f2(j)+c。试推导出函数f1、f2和常数c(要求f1和f2中不含常数项)。 5.4 设有一个准对角矩阵 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − −− − mm mm mm mm a aa aa aa aa a aa 2,212,2 2,1212,12 4443 3433 21 22 1211 ...... ...... 按以下方式存于一维数组 B[4m]中: 0 1 2 3 4 5 6 k 4m-2 4m-1 a11 a12 a21 a22 a33 a34 a43 ... aij ... a2m-1,2m a2m,2m 第 6 页

写出由一对下标(i,)求k的转换公式。 5.5己知稀疏矩阵A4×5如下: 「01005] 4=23060 00000 04007 (1)用三元组表作为存储结构,绘出相应的三元组表示意图: (2)用十字链表作为存储结构,绘出相应的十字链表示意图。 5.6设稀疏矩阵A和B均以三元组顺序表作为存储结构。试写出计算矩阵相加C =A十B的算法,其中,C是另设的、存放结果的三元组表(提示:可用类似于两 个有序顺序表归并的处理方法)。 5.7试编写一个算法,实现以三元组的形式打印用十字链表表示的稀疏矩阵中所 有非零元素及其下标。 5.8试编写一个算法,实现以矩形阵列的形式打印用十字链表表示的稀疏矩阵。 第六章树和二叉树 6.1试分别绘出具有3个结点的树和3个结点的二叉树的所有不同形态。 6.2设结点X是二叉树上一个度为1的结点,X有几个子树? 6.3描述满足下列条件的二叉树形态。 (1)先序遍历序列与中序遍历序列相同: (②)后序遍历序列与中序遍历序列相同: (3)先序遍历序列与后序遍历序列相同: 6.4一个深度为H的满k叉树有如下性质:第H层上所有结点都是叶子结点,其 余各层上每个结点都有k棵非空子树。如果从1开始按自上而下、自左向右的次 序对全部结点编号,问: (1)各层的结点数目是多少? (②)编号为1的结点的父结点(若存在)的编号是多少? (3)编号为i的结点的第j个孩子(若存在)的编号是多少? (④)编号为1的结点有右兄弟的条件是什么?其右兄弟的编号是多少? 第7页
写出由一对下标(i,j)求 k 的转换公式。 5.5 已知稀疏矩阵 A4×5 如下: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 70040 00000 06032 50010 A (1)用三元组表作为存储结构,绘出相应的三元组表示意图; (2)用十字链表作为存储结构,绘出相应的十字链表示意图。 5.6 设稀疏矩阵A和B 均以三元组顺序表作为存储结构。试写出计算矩阵相加 C =A+B 的算法,其中,C 是另设的、存放结果的三元组表(提示:可用类似于两 个有序顺序表归并的处理方法)。 5.7 试编写一个算法,实现以三元组的形式打印用十字链表表示的稀疏矩阵中所 有非零元素及其下标。 5.8 试编写一个算法,实现以矩形阵列的形式打印用十字链表表示的稀疏矩阵。 第六章 树和二叉树 6.1 试分别绘出具有 3 个结点的树和 3 个结点的二叉树的所有不同形态。 6.2 设结点 X 是二叉树上一个度为 1 的结点,X 有几个子树? 6.3 描述满足下列条件的二叉树形态: (1) 先序遍历序列与中序遍历序列相同; (2) 后序遍历序列与中序遍历序列相同; (3) 先序遍历序列与后序遍历序列相同; 6.4 一个深度为 H 的满 k 叉树有如下性质:第 H 层上所有结点都是叶子结点,其 余各层上每个结点都有 k 棵非空子树。如果从 1 开始按自上而下、自左向右的次 序对全部结点编号,问: (1) 各层的结点数目是多少? (2) 编号为 i 的结点的父结点(若存在)的编号是多少? (3) 编号为 i 的结点的第 j 个孩子(若存在)的编号是多少? (4) 编号为 i 的结点有右兄弟的条件是什么?其右兄弟的编号是多少? 第 7 页
6.5己知一棵度为k的树中有l个度为1的结点,n2个度为2的结点,, k个度为k的结点,问该树中有多少个叶子结点? 6.6已知在一棵含有个结点的树中,只有度为k的分支结点和度为0的叶子结 点。试求该树含有的叶子结点的数目。 6.7设n和m为二叉树中两个结点,用“1”、“0”、和“0”(分别表示肯定,否 定和不一定)填写下表: 已知 问 先序遍历时 中序遍历时 后序遍历时 n在m之前? n在m之前? n在m之前? n在m左方 n在m右方 n是m祖先 n是m子孙 (注:如果离n和m的最近的共同祖先X存在,且位于X的左子树中,m位于X的右子树 中,则称“n在m的左方”或“m在n的右方”) 6.8己知一棵树如图6-1所示,画出与该树对应的二叉树,并写出该树的先根遍 历序列和后根遍历序列。 G 图6-1 6.9将如图6-2所示的森林转化为对应的二叉树。 第8页
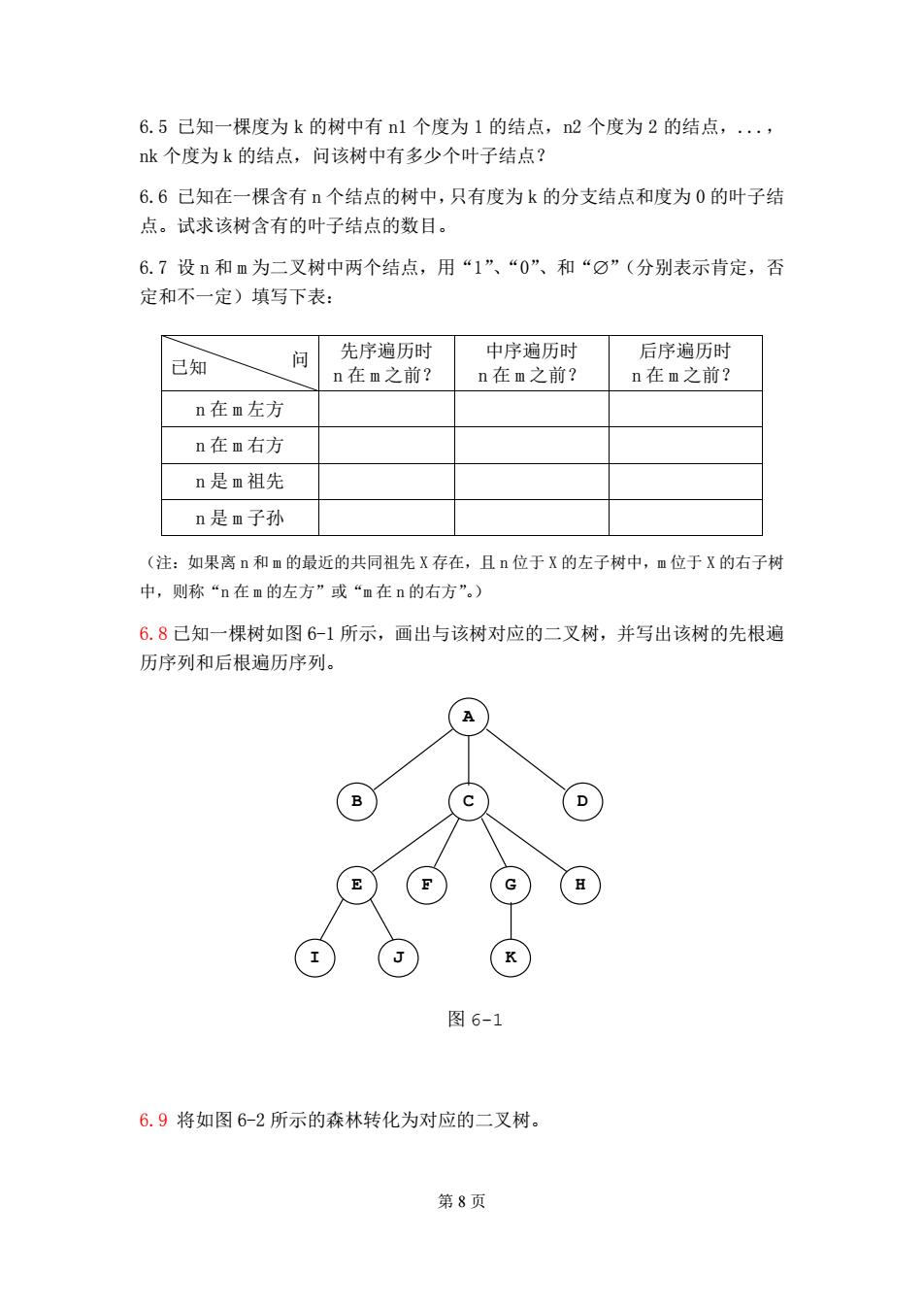
第 8 页 6.5 已知一棵度为 k 的树中有 n1 个度为 1 的结点,n2 个度为 2 的结点,..., nk 个度为 k 的结点,问该树中有多少个叶子结点? 6.6 已知在一棵含有 n 个结点的树中,只有度为 k 的分支结点和度为 0 的叶子结 点。试求该树含有的叶子结点的数目。 6.7 设n和m 为二叉树中两个结点,用“1”、“0”、和“∅”(分别表示肯定,否 定和不一定)填写下表: 已知 问 先序遍历时 n 在 m 之前? 中序遍历时 n 在 m 之前? 后序遍历时 n 在 m 之前? n 在 m 左方 n 在 m 右方 n 是 m 祖先 n 是 m 子孙 (注:如果离 n 和 m 的最近的共同祖先 X 存在,且 n 位于 X 的左子树中,m 位于 X 的右子树 中,则称“n 在 m 的左方”或“m 在 n 的右方”。) 6.8 已知一棵树如图 6-1 所示,画出与该树对应的二叉树,并写出该树的先根遍 历序列和后根遍历序列。 6.9 将如图 6-2 所示的森林转化为对应的二叉树。 A B C D E F G H I J K 图 6-1
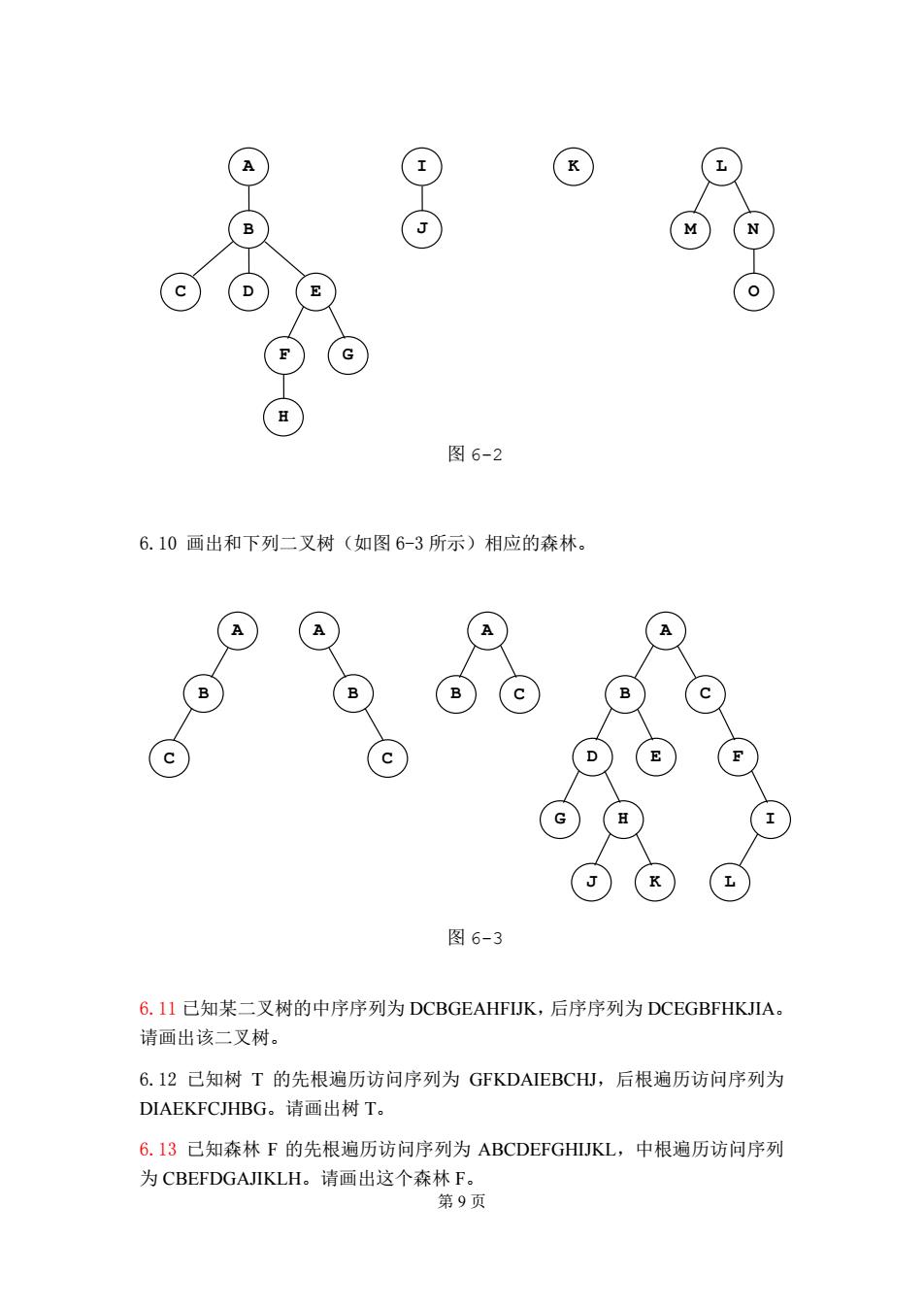
B (D)(E B 图6-2 6.10画出和下列二叉树(如图6-3所示)相应的森林。 A B ⑧⊙ c c D E (H ⊙R 图6-3 6,11己知某二叉树的中序序列为DCBGEAHFIJK,后序序列为DCEGBFHKJIA。 请画出该二叉树。 6.12已知树T的先根遍历访问序列为GFKDAIEBCH,后根遍历访问序列为 DIAEKFCJHBG。请画出树T。 6.13已知森林F的先根遍历访问序列为ABCDEFGHIJKL,中根遍历访问序列 为CBEFDGAJIKLH。请画出这个森林F。 第9页
K 图 6-2 A C D E B F G H J I L M N O 6.10 画出和下列二叉树(如图 6-3 所示)相应的森林。 图 6-3 A B C C A B C A B A D E B C F G H J K L I 6.11 已知某二叉树的中序序列为 DCBGEAHFIJK,后序序列为 DCEGBFHKJIA。 请画出该二叉树。 6.12 已知树 T 的先根遍历访问序列为 GFKDAIEBCHJ,后根遍历访问序列为 DIAEKFCJHBG。请画出树 T。 6.13 已知森林 F 的先根遍历访问序列为 ABCDEFGHIJKL,中根遍历访问序列 为 CBEFDGAJIKLH。请画出这个森林 F。 第 9 页

6.14假设某个电文由(a,b,c,d,e,E,g,h)8个字母组成,每个字母在电文中出现 的次数分别为(7,19,2,6,32,3,21,10),试解答下列问题: (1)画出出huffman树: (②)写出每个字母的huffman编码: (3)在对该电文进行最优二进制编码处理后,电文的二进制位数。 6.15写出复制一棵二叉树的算法。 6.16试编写算法,实现将二叉树所有结点的左右子树互换。 6.17写出按层次遍历二叉树的算法. 6.18写出判断给定二叉树是否为完全二叉树的算法。 6.19写出判断两棵给定二叉树是否相似的算法。 (注:两棵二叉树B1和B2相似是指:B1和B2皆空,或者皆不空且B1的左、右 子树和B2的左、右子树分别相似。) 6.20利用栈的基本操作,写出二叉树先序遍历的非递归算法。 6.21写出统计树中叶子结点个数的算法,树用孩子兄弟链表表示。 6.22写出计算树的深度的算法,树用孩子兄弟链表表示。 6.23写出计算二叉树第K层结点数的算法。 6.24写出计算二叉树宽度的算法。 第七章图 (v1) 7.1已知有向图如图7-1所示, 请给出该图的 (1)邻接矩阵示意图 (2)邻接表示意图 V2 (3)逆邻接表 (4)所有强连通分量 第10页 图7-1
第 10 页 图 7-1 V5 V2 V4 V3 V1 V6 6.14 假设某个电文由(a,b,c,d,e,f,g,h)8 个字母组成,每个字母在电文中出现 的次数分别为(7,19,2,6,32,3,21,10),试解答下列问题: (1) 画出出 huffman 树; (2) 写出每个字母的 huffman 编码; (3) 在对该电文进行最优二进制编码处理后,电文的二进制位数。 6.15 写出复制一棵二叉树的算法。 6.16 试编写算法,实现将二叉树所有结点的左右子树互换。 6.17 写出按层次遍历二叉树的算法。 6.18 写出判断给定二叉树是否为完全二叉树的算法。 6.19 写出判断两棵给定二叉树是否相似的算法。 (注:两棵二叉树 B1 和 B2 相似是指:B1 和 B2 皆空,或者皆不空且 B1 的左、右 子树和 B2 的左、右子树分别相似。) 6.20 利用栈的基本操作,写出二叉树先序遍历的非递归算法。 6.21 写出统计树中叶子结点个数的算法,树用孩子兄弟链表表示。 6.22 写出计算树的深度的算法,树用孩子兄弟链表表示。 6.23 写出计算二叉树第 K 层结点数的算法。 6.24 写出计算二叉树宽度的算法。 第七章 图 7.1 已知有向图如图 7-1 所示, 请给出该图的 (1)邻接矩阵示意图 (2)邻接表示意图 (3)逆邻接表 (4)所有强连通分量