
第6章图 6.1图的基本概念 6.2图的表示与实现 6.3图的遍历 6.4最小生成树 6.5拓扑排序 6.6关键路径 6.7最短路径 6.8最大流问题* ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 1 中国科学技术大学 第6章 图 6.1图的基本概念 6.2图的表示与实现 6.3图的遍历 6.4最小生成树 6.5拓扑排序 6.6关键路径 6.7最短路径 6.8最大流问题*

6.1图的基本概念 图(graph): 一个顶点(vertex)的有穷集V(G)和一个弧(arc)的 集合E(G)组成。记做:G=(V,E)。V是数据结构中 的数据元素,E是集合上的关系 ·弧(arc)、弧头(终点)、弧尾(起点) -表从v到w的弧 。1 有向图(digraph)、无向图(undigraph)、边: -(V,w)代表和 。 有向网、无向网: 一带权的有向图和无向图 。 完全图(complete graph):边e为n(n-l)/2 ·有向完全图:弧e为n(n-l) ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 2 中国科学技术大学 6.1图的基本概念 • 图(graph): – 一个顶点(vertex)的有穷集V(G)和一个弧(arc)的 集合E(G)组成。记做:G=(V,E)。V是数据结构中 的数据元素,E是集合上的关系 • 弧(arc)、弧头(终点)、弧尾(起点): – 表从v到w的弧 • 有向图(digraph) 、无向图(undigraph) 、边: – (v,w)代表和 • 有向网、无向网: – 带权的有向图和无向图 • 完全图(complete graph):边e为n(n-1)/2 • 有向完全图:弧e为n(n-1)
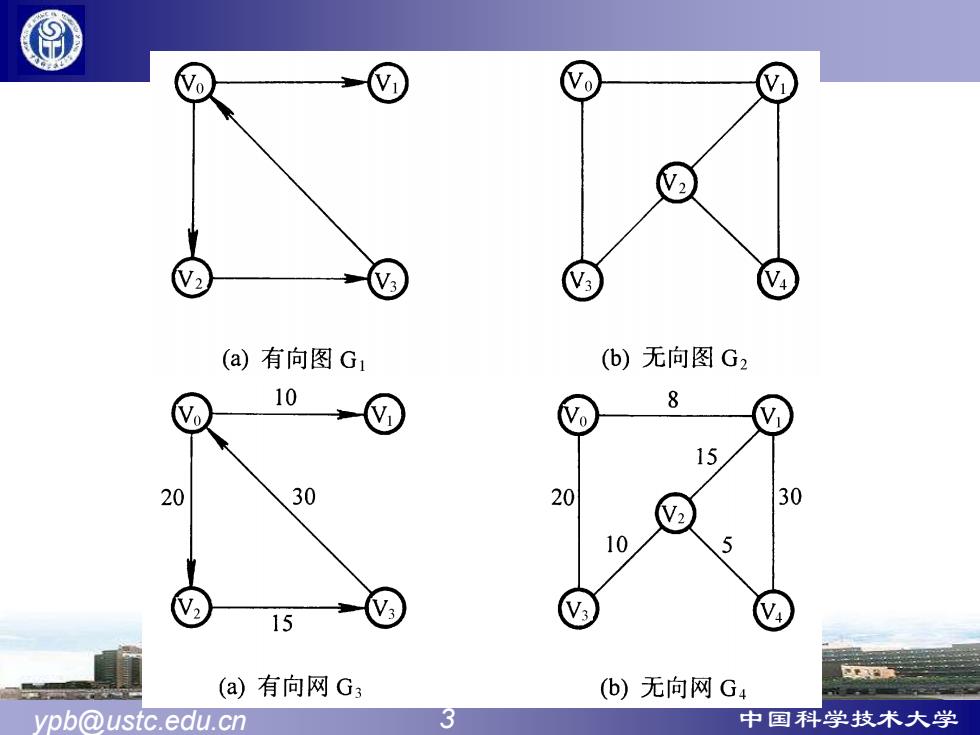
N3 V (a)有向图G1 (b)无向图G2 10 8 Vo 15 20 30 20 30 10 15 (a)有向网G3 (b)无向网G4 ypb@ustc.edu.cn 3 中国科学技术大学
ypb@ustc.edu.cn 3 中国科学技术大学

稀疏图(sparse graph):有向图enlogn 。 子图(subgraph): G=(V,E),G'=(V”,E),如V”≤V且E≤E',则称G是G的子图 度(degree)、出度(OutDegree)、入度(ndegree): - 称u邻接到v,或v邻接自u。邻接到某顶点的弧的数目称该顶 点的入度D(v);邻接自某顶点的弧的数目称该顶点的出度OD(u); 某顶点的入度、出度之和为该顶点的度TD() ·路径和回路: 一有向路径无向路径,路径长度、回路或环 ·连通图和连通分量: - 连通图(无向),强连通图(有向),连通分量 生成树和生成森林(所有顶点/连通图/无回路) ypb@ustc.edu.cn 4 中国科学技术大学
ypb@ustc.edu.cn 4 中国科学技术大学 • 稀疏图(sparse graph):有向图enlogn • 子图(subgraph): – G=(V,E),G’=(V’,E’),如V’≦V且E≦E’,则称G’是G的子图 • 度(degree)、出度(OutDegree)、入度(Indegree): – 称u邻接到v,或v邻接自u。邻接到某顶点的弧的数目称该顶 点的入度ID(v);邻接自某顶点的弧的数目称该顶点的出度OD(u); 某顶点的入度、出度之和为该顶点的度TD(v) • 路径和回路: – 有向路径/无向路径,路径长度、回路或环 • 连通图和连通分量: – 连通图(无向),强连通图(有向),连通分量 • 生成树和生成森林(所有顶点/连通图/无回路)

图的ADT描述 ADT Graph{ 数据对象V: V是同类型数据元素的非空有限集,称为顶点集。 数据关系R: R={Kv,v>vi,v;∈V且Path(vi,v),vi,v>表示从v 到v的弧,谓词Path(v,v)定义了弧的意义和信 息} 基本操作 CreateGraph(&G,V,E) DestroyGraph(&G) ypb@ustc.edu.cn 5 中国科学技术大学
ypb@ustc.edu.cn 5 中国科学技术大学 图的ADT描述 ADT Graph{ 数据对象V: V是同类型数据元素的非空有限集,称为顶点集。 数据关系R: R={|vi,vj∈V且Path(vi,vj),表示从vi 到vj的弧,谓词Path(vi,vj)定义了弧的意义和信 息} 基本操作: – CreateGraph(&G, V, E) – DestroyGraph(&G)

LocateVex(G,u) -GetVex(G,v) PutVex(&G,v,value) FirstAdjVex(G,v) -NextAdjVex(G,v,w) -InsertVex(&G,v) Delete Vex(&G,v) InsertArc(&G,v,w) -DeleteArc(&G,v,w) -DFSTraverse(G,v,visit()) -BFSTraverse(G,v,visit()) end ADT Graph ypb@ustc.edu.cn 6 中国科学技术大学
ypb@ustc.edu.cn 6 中国科学技术大学 – LocateVex(G,u) – GetVex(G,v) – PutVex(&G,v,value) – FirstAdjVex(G,v) – NextAdjVex(G,v,w) – InsertVex(&G,v) – DeleteVex(&G,v) – InsertArc(&G,v,w) – DeleteArc(&G,v,w) – DFSTraverse(G,v,visit()) – BFSTraverse(G,v,visit()) } end ADT Graph

6.2图的表示与实现 图的数组(邻接矩阵)存储表示 typedef enum(DG,DN,AG,AN}GraphKind typedef int ArcType typedef struct{ VertexType vexs[MAX_V_NUM]; ArcType arcs [MAX V NUM][MAX V NUM]; int vexnum arcnum; GraphKind kind; }MGraph; ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 7 中国科学技术大学 6.2图的表示与实现 ➢ 图的数组(邻接矩阵)存储表示 typedef enum{DG,DN,AG,AN} GraphKind; typedef int ArcType; typedef struct{ VertexType vexs[MAX_V_NUM]; ArcType arcs [MAX_V_NUM][ MAX_V_NUM]; int vexnum,arcnum; GraphKind kind; }MGraph;

0 1 1 0 ∞ P ∞ 20 ∞ 8 o∞ 15 00 0 0 0 30 0 A1= A2= ∞ 15 ∞ 10 5 0 0 0 20 ∞ 10 ∞ O∞ 0 30 5 (a)G,的邻接矩阵 (b)G4的邻接矩阵 ypb@ustc.edu.cn 8 中国科学技术大学
ypb@ustc.edu.cn 8 中国科学技术大学

部分操作的实现 void CreateGraph(MGraph &G) int LocateVex(MGraph G,VertexType v) void InsertArc(MGraph &G,VertexType vi, VertexType vj) int FirstAdjVex(MGraph G,int v) int NextAdiVex(MGraph G,int v,int w) ypb@ustc.edu.cn 9 中国科学技术大学
ypb@ustc.edu.cn 9 中国科学技术大学 部分操作的实现 • void CreateGraph(MGraph &G) • int LocateVex(MGraph G, VertexType v) • void InsertArc(MGraph &G, VertexType vi, VertexType vj) • int FirstAdjVex(MGraph G, int v) • int NextAdjVex(MGraph G, int v, int w)

void CreateGraph(MGraph &G){ ∥从键盘输入图顶点和边集,创建用邻接矩阵表示的图G cin>>G.vexnum>>G.arcnum>>G.kind; for(i=0;i>G.vexs[i];/输入顶点集 for(i=0;i>vi>>j;1/输入弧 i=LocateVex(G,vi);/求顶点vi的存储位置下标 j=LocateVex(G,);l/求顶点vj的存储位置下标 G.arcs[i]]=1; /置弧 if(G.kind==2)G.arcs][叮=1;l无向图,置对称弧 }//CreateGraph
void CreateGraph(MGraph &G){ //从键盘输入图顶点和边集,创建用邻接矩阵表示的图G cin>>G.vexnum>>G.arcnum>>G.kind; for(i=0;i>G.vexs[i]; //输入顶点集 for(i=0;i>vi>>vj; //输入弧 i=LocateVex(G,vi); //求顶点vi的存储位置下标 j=LocateVex(G,vj); //求顶点vj的存储位置下标 G.arcs[i][j]=1; //置弧 if(G.kind==2) G.arcs[j][i]=1; //无向图,置对称弧 } } //CreateGraph