
第5章二叉树和树 5.1树的基本概念 5.2二叉树的概念 5.3二叉树的遍历及应用 5.4线索二叉树 5.5树和森林 5.6哈夫曼树和哈夫曼编码 是 ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 1 中国科学技术大学 第5章 二叉树和树 5.1树的基本概念 5.2二叉树的概念 5.3二叉树的遍历及应用 5.4线索二叉树 5.5树和森林 5.6哈夫曼树和哈夫曼编码

5.1树的基本概念 B H ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 2 中国科学技术大学 5.1树的基本概念 • 树的定义(无序树) – n(n>=0)个数据元素(结点)的有限集D,若D为 空集,则为空树。否则: – 在D中存在唯一的称为根的数据元素 – 当n>1时,其余结点可分为m(m>0)个互不相交 的有限子集T1,T2,......,Tm,其中每个子集本 身又是一颗树,并成为根的子树

树的ADT描述 ADT Tree 数据对象D:D是同类型数据元素的集合。 数据关系R:若D=O,则称为空树; 否则R是满足下列条件的二元关系: (I)D中存在唯一的称为根的元素root,它在R下无直接前驱。 (2)若D-{root}=0,则R=☑;否则存在D-{root}的一个划分 D1,D2,.Dm(m>0),对任意的jk(1,k≤m),有DinDk=0, 且对任意的i(I≤ism),存在唯一的数据元素xi∈Di,有∈R; (3)对应于D-{root}的划分,R-{,}有 唯一的一个划分R1,.,Rm(m>0),对任意的j(1j,k≤m) 有RjORk=☑,且对任意的i(I≤ism),Ri是Di上的二元关系。 (Di,Ri是一棵符合本定义的树,称为根root的子树。 ypb@ustc.edu.cn 3 中国科学技术大学
ypb@ustc.edu.cn 3 中国科学技术大学 树的ADT描述 ADT Tree{ 数据对象D:D是同类型数据元素的集合。 数据关系R:若D=,则称为空树; 否则R是满足下列条件的二元关系: (1)D中存在唯一的称为根的元素root,它在R下无直接前驱。 (2)若D-{root}=,则R=;否则存在D-{root}的一个划分 D1,D2,...Dm(m>0),对任意的j≠k(1≤j,k≤m),有Dj∩Dk=, 且对任意的i(1≤i≤m),存在唯一的数据元素xi∈Di,有∈R; (3)对应于D-{root}的划分,R-{,...}有 唯一的一个划分R1,...,Rm(m>0),对任意的j≠k(1≤j,k≤m) 有Rj∩Rk=,且对任意的i(1≤i≤m),Ri是Di上的二元关系。 (Di,Ri)是一棵符合本定义的树,称为根root的子树

S 基本操作: -nitTree(&T) -DestroyTree (&T) CreateTree(&T.definition) TreeEmpty(T) TreeDepth(T) Root(T) - Parent(T,x) FirstChild (T,x) Nextsibling(T,x) - InsertChild (&T,x,i,p) - DeleteChild (&T,x,i 一 Traverse(T,visit()) }End ADT Tree ypb@ustc.edu.cn 4 中国科学技术大学
ypb@ustc.edu.cn 4 中国科学技术大学 基本操作: – InitTree(&T) – DestroyTree(&T) – CreateTree(&T,definition) – TreeEmpty(T) – TreeDepth(T) – Root(T) – Parent(T, x) – FirstChild(T,x) – Nextsibling(T,x) – InsertChild(&T,x,i,p) – DeleteChild(&T,x,i) – Traverse(T,visit()) }End ADT Tree

树的相关术语 。 结点:树的数据元素及指向子树的分支。 ·结点的度:子树的个数。 ·树的度:树中结点度的最大值。 分支结点、叶子结点:度不为0、为0的结点。 。 孩子:结点子树的根(后继)称为该结点孩子。 ·双亲: 结点前驱称该结点双亲。 。 兄弟、祖先、子孙: ·结点层次:根结点层次是1,其他结点层次是双 亲层次+1。 。 树深度:结点层次的最大值。 无序树:交互子树不是不同的树。 。 森林:m(m>0)个不相交的树构成森林。 ypb@ustc.edu.cn 5 中国科学技术大学
ypb@ustc.edu.cn 5 中国科学技术大学 树的相关术语 • 结点:树的数据元素及指向子树的分支。 • 结点的度:子树的个数。 • 树的度:树中结点度的最大值。 • 分支结点、叶子结点:度不为0、为0的结点。 • 孩子:结点子树的根(后继)称为该结点孩子。 • 双亲:结点前驱称该结点双亲。 • 兄弟、祖先、子孙: • 结点层次:根结点层次是1,其他结点层次是双 亲层次+1。 • 树深度:结点层次的最大值。 • 无序树:交互子树不是不同的树。 • 森林:m(m>=0)个不相交的树构成森林

树的性质 性质1n个结点,每个结点度d,则:n=∑d,+1 性质2:度为k的树第层的结点个数最多k() ·性质3:深度为h的k叉树,最多结点数为 k-1 k-1 ·性质4:具有n个结点的k叉树深度最小为 1ogk(n(k-1)+1)] ypb@ustc.edu.cn 6 中国科学技术大学
ypb@ustc.edu.cn 6 中国科学技术大学 树的性质 • 性质1:n个结点,每个结点度di ,则: • 性质2:度为k的树第i层的结点个数最多 k (i-1) • 性质3:深度为h的k叉树,最多结点数为 • 性质4:具有n个结点的k叉树深度最小为 • 1 1 = + = n i n di 1 1 − − k k h logk (n(k −1) +1)

5.2二叉树(binary Tree) 二叉树的定义和基本术语 是n(n≥0)个元素的有限集,或为空集(n=0),或含有唯 一的根元素,其余元素分成两个互不相交的子集,每 个子集本身也是一颗二叉树。分别称为根的左子树、 右子树。 -空树集合为空的二叉树 一结点的度:非空子树的个数 一左孩子,右孩子 -叶子结点:左右子树均空的结点;度为零 二叉树的深度:二叉树中叶子结点的最大层次数 ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 7 中国科学技术大学 ➢ 二叉树的定义和基本术语 – 是n(n0)个元素的有限集,或为空集(n=0) ,或含有唯 一的根元素,其余元素分成两个互不相交的子集,每 个子集本身也是一颗二叉树。分别称为根的左子树、 右子树。 – 空树:集合为空的二叉树 – 结点的度:非空子树的个数 – 左孩子,右孩子 – 叶子结点:左右子树均空的结点;度为零 – 二叉树的深度:二叉树中叶子结点的最大层次数 5.2二叉树(binary Tree)
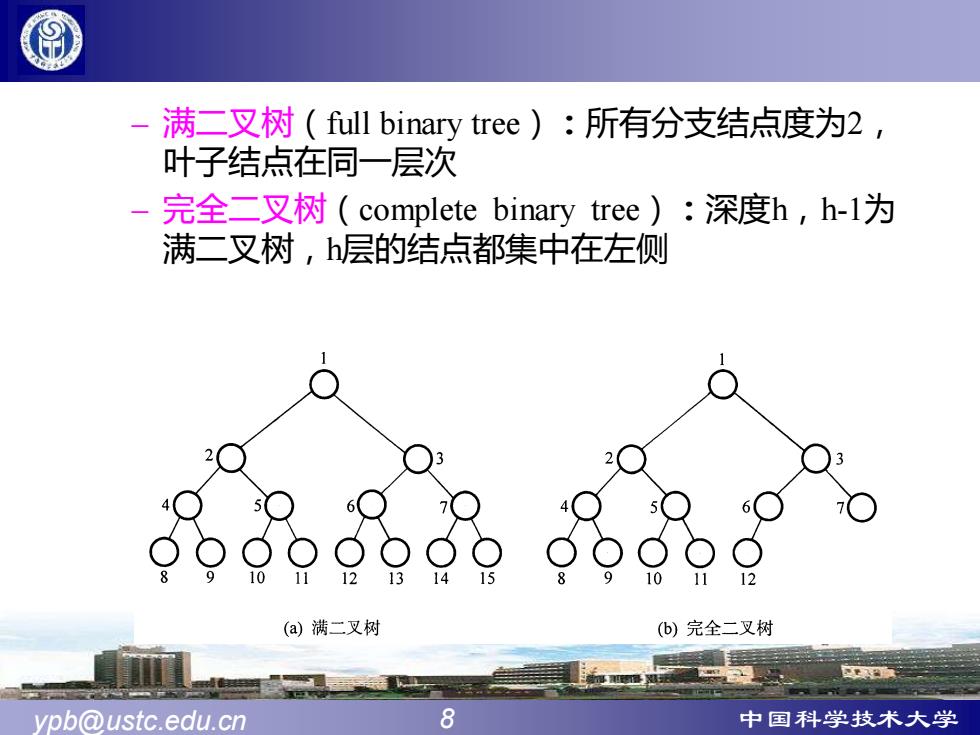
满二叉树(full binary tree):所有分支结点度为2, 叶子结点在同一层次 -完全二叉树(complete binary tree):深度h,h-l为 满二叉树,h层的结点都集中在左侧 o品o品品品o品%。 (a)满二又树 (b)完全二叉树 ypb@ustc.edu.cn 8 中国科学技术大学
ypb@ustc.edu.cn 8 中国科学技术大学 – 满二叉树(full binary tree):所有分支结点度为2, 叶子结点在同一层次 – 完全二叉树(complete binary tree):深度h,h-1为 满二叉树,h层的结点都集中在左侧

二叉树ADT描述 ADT BinaryTreef 数据对象D:D是同类型数据元素的集合。 数据关系R:若D=O,则称BinaryTree:为空二叉树; 否则R是满足下列条件的二元关系: (1)在D中存在唯一的称为根的元素root,它在R下无直接前驱; (2)若D-{root}=☑,则R=O;否则存在D-{root}={DI,Dr}, 且DInDr=-O; (3)若Dl≠O,则DI中存在唯一的元素xl,∈R,且存在 DI上的关系RlcR;若Dr≠☑,则Dr中存在唯一的元素xr, ∈R,且存在Dr上的关系RrCR;R={, ,Rl,Rr}i (4)D1,)是一棵符合本定义的二叉树,称为根的左子树; (Dr,R)是一棵符合本定义的二叉树,称为根的右子树。 ypb@ustc.edu.cn 9 中国科学技术大学
ypb@ustc.edu.cn 9 中国科学技术大学 二叉树ADT描述 ADT BinaryTree{ 数据对象D:D是同类型数据元素的集合。 数据关系R:若D=,则称BinaryTree为空二叉树; 否则R是满足下列条件的二元关系: (1)在D中存在唯一的称为根的元素root,它在R下无直接前驱; (2)若D-{root}=,则R=;否则存在D-{root}={Dl,Dr}, 且Dl∩Dr=; (3)若Dl≠,则Dl中存在唯一的元素xl,∈R,且存在 Dl上的关系RlR;若Dr≠,则Dr中存在唯一的元素xr, ∈R,且存在Dr上的关系RrR;R={, ,Rl,Rr}; (4)(Dl,Rl)是一棵符合本定义的二叉树,称为根的左子树; (Dr,Rr)是一棵符合本定义的二叉树,称为根的右子树

S 基本操作P: .InitBiTree(&T) .RightChild(T,e) .DestroyBiTree(&T) .LeftSibling(T,e) .CreateBiTree(&T,definition) RightSibling(T,e) .BiTreeEmpty(T) .InsertChild(&T,p,LR,C) .BiTreeDepth(T) DeleteChild(&T,p,LR) .Parent(T,e) .Traverse(T) .LeftChild(T,e) }//End ADT BinaryTree ypb@ustc.edu.cn 10 中国科学技术大学
ypb@ustc.edu.cn 10 中国科学技术大学 •InitBiTree(&T) •DestroyBiTree(&T) •CreateBiTree(&T,definition) •BiTreeEmpty(T) •BiTreeDepth(T) •Parent(T,e) •LeftChild(T,e) •RightChild(T,e) •LeftSibling(T,e) •RightSibling(T,e) •InsertChild(&T,p,LR,C) •DeleteChild(&T,p,LR) •Traverse(T) 基本操作P: }//End ADT BinaryTree