
第九章查找表 。9.1静态查找表 。9.2动态查找表 ·9.3哈希表及其查找 ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 1 中国科学技术大学 第九章 查找表 • 9.1静态查找表 • 9.2动态查找表 • 9.3哈希表及其查找

查找表: - 由同一类元素或记录构成的集合。对数据元素间的关系未作限定。 对查找表的操作有 查找某个“特定”【 的元素是否在表中。 一查找某个“特点”的元素的各种属性。 - 在查找表中插入一个元素。 一在查找表中删除一个元素 ·静态查找表、动态查找表 。 关键字 数据元素中的某个数据项值。可以表示一个数据元素,如可以唯一 表示,则为主关键字(primary key)。 。 查找 一根据给定的某个值,在查找表中确定一个关键字等于给定值的数据 元素。若找到表示查找成功,返回该元素详细信息或在查找表中的 位置;否则返回NULL ypb@ustc.edu.cn 2 中国科学技术大学
ypb@ustc.edu.cn 2 中国科学技术大学 • 查找表: – 由同一类元素或记录构成的集合。对数据元素间的关系未作限定。 • 对查找表的操作有 – 查找某个“特定”的元素是否在表中。 – 查找某个“特点”的元素的各种属性。 – 在查找表中插入一个元素。 – 在查找表中删除一个元素 • 静态查找表、动态查找表 • 关键字 – 数据元素中的某个数据项值。可以表示一个数据元素,如可以唯一 表示,则为主关键字(primary key)。 • 查找 – 根据给定的某个值,在查找表中确定一个关键字等于给定值的数据 元素。若找到表示查找成功,返回该元素详细信息或在查找表中的 位置;否则返回NULL

9.1静态查找表 9.1.1顺序查找 typdef struct ElemType*elem,/元素存储空间,0单元保留 int length;/表长度 }SSTable; 。 查找成功和失败 。平均查找长度 一查找过程中先后和给定值进行比较的关键字的个数 的期望值 ASL=>P;Ci Pi=1 i=1,2,......n C:=n-i+1P:=1/n ASLss=1/nΣ(n-i+1)=(n+1)/2 ypb@ustc.edu.cn 3 中国科学技术大学
ypb@ustc.edu.cn 3 中国科学技术大学 9.1静态查找表 9.1.1顺序查找 typdef struct{ ElemType *elem; //元素存储空间,0单元保留 int length; //表长度 }SSTable; • 查找成功和失败 • 平均查找长度 – 查找过程中先后和给定值进行比较的关键字的个数 的期望值 ASL=∑PiCi ∑Pi=1 i=1,2,……n Ci=n-i+1 Pi=1/n ASLss=1/n∑(n-i+1)=(n+1)/2

9.1.2折半查找 ·折半查找(binary Search):二分查找。 ·例8.2利用二分查找在顺序有序表中查找。 -8.2 Int Search Bin(SStable ST,KeyType kval) ASLbs (n+1)/nlog (n+1)-1 ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 4 中国科学技术大学 9.1.2折半查找 • 折半查找(binary Search):二分查找。 • 例8.2 利用二分查找在顺序有序表中查找。 – 算法8.2 Int Search_Bin(SStable ST,KeyType kval) –ASLbs=(n+1)/nlog(n+1)-1

二分查找平均查找长度(假设满二叉树) ASLos=(n+1)/nlog(n+1)-1 ASLs-(2+21*2+.+2.1*h)Pi-是7i*21-1(=2h-1)) 令:S-1*2-1=-2211*2-2t+2骆-1(t+1)2t-1 =2∑0-1t*2t-1+2∑0-12t-1 =2(∑7t*2t-1-h*2h-1)+∑b-12 =2(S-h*2h-1)+2h-1 所以:S=h*2h-2h+1=(n+1)log2(n+1)-n ASLo-1s=+110g2(n+1)-1 ypb@ustc.edu.cn 5 中国科学技术大学
ypb@ustc.edu.cn 5 中国科学技术大学 二分查找平均查找长度(假设满二叉树) ASLbs=(n+1)/nlog(n+1)-1 ASLbs=(2 0+2 1*2+…+2 h-1*h)Pi=

9.1.3分块查找 又称索引顺序查找 一介于顺序查和折半查找之间。适合于关键字分块有序 typedefstruct{ KeyType key; int stadr; indexltem; typedefstruct{ indexItem *elem; int length; }indexTable; -Search Idx(SSTable ST,indexTable ID,KeyT kval) -设索引长度b,顺序表长度为n,则: ASLidx=ASL(b)+ASL(n/b)~log2(b+1)-1+(n/b+1)/2 ypb@ustc.edu.cn 6 中国科学技术大学
ypb@ustc.edu.cn 6 中国科学技术大学 • 又称索引顺序查找 – 介于顺序查和折半查找之间。适合于关键字分块有序 typedefstruct { KeyType key; int stadr; }indexItem; typedefstruct{ indexItem *elem; int length; }indexTable; – 算法Search_Idx(SSTable ST,indexTable ID, KeyT kval) – 设索引长度b,顺序表长度为n,则: ASLidx=ASL(b)+ASL(n/b)≈log2 (b+1)-1+(n/b+1)/2 9.1.3分块查找
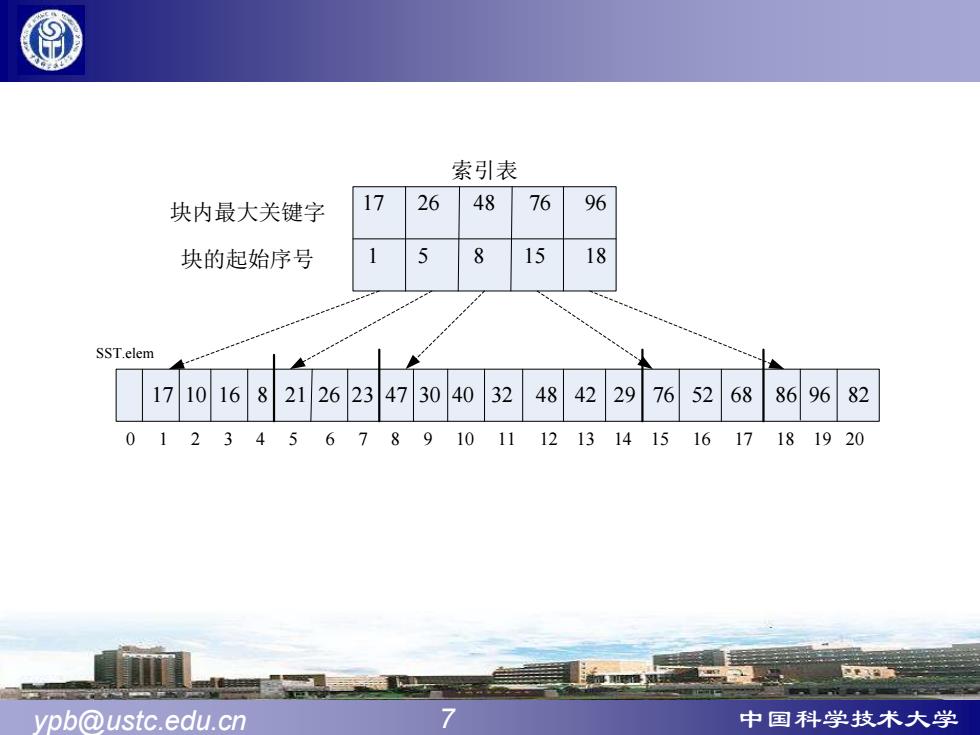
索引表 块内最大关键字 17 26 48 76 96 块的起始序号 8 15 18 SST.elem 171016 8 212623473040 32 48422976 5268 8696 82 01234567891011121314151617181920 ypb@ustc.edu.cn 中国科学技术大学
ypb@ustc.edu.cn 7 中国科学技术大学 索引表 17 26 48 76 96 1 5 8 15 18 块内最大关键字 块的起始序号 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 17 10 16 8 21 26 23 47 30 40 32 48 42 29 76 52 68 86 96 82 SST.elem

9.2动态查找表 ADT DynamicSearchTable 数据对象:D是具有相同特性的元素集合。 数据关系:同属集合关系。 基本操作: InitDSTable (&DT DestroyDSTable (&DT -SearchDSTable DT,kval InsertDSTable &DT,e DeleteDSTable (&DT,kval ) TraverseDSTable (DT,Visit()) ADT DynamicSearchTable; ypb@ustc.edu.cn 8 中国科学技术大学
ypb@ustc.edu.cn 8 中国科学技术大学 9.2动态查找表 ADT DynamicSearchTable{ 数据对象:D是具有相同特性的元素集合。 数据关系:同属集合关系。 基本操作: – InitDSTable(&DT) – DestroyDSTable(&DT) – SearchDSTable(DT,kval) – InsertDSTable(&DT,e) * – DeleteDSTable(&DT,kval) * – TraverseDSTable(DT,Visit()) }ADT DynamicSearchTable;

9.2.1二叉查找树 ·查找树、二叉查找树 -通过和根结点的关键字进行比较可以将继续查找的范 围缩小到某一颗子树中,具有该特性的树称查找树。 二叉查找树又称二叉排序树。 ·例:二叉查找树的查询过程。 Status Search BST(BiTree T,KeyType kval,BiTree f. BiTree &p) ·例二叉查找树的插入算法 Status Insert BST(BiTree &T,ElemType e) ypb@ustc.edu.cn 9 中国科学技术大学
ypb@ustc.edu.cn 9 中国科学技术大学 9.2.1二叉查找树 • 查找树、二叉查找树 – 通过和根结点的关键字进行比较可以将继续查找的范 围缩小到某一颗子树中,具有该特性的树称查找树。 二叉查找树又称二叉排序树。 • 例:二叉查找树的查询过程。 Status Search_BST(BiTree T,KeyType kval,BiTree f, BiTree &p) • 例:二叉查找树的插入算法 Status Insert_BST(BiTree &T, ElemType e)

删除结点的处理方法 1)若是叶子结点,直接删除 2)只有一个孩子,则将其孩子直接挂到其双亲上。 3)有两个孩子,找左孩子中最大的一个元素,代替被 删除结点,最大元素肯定只有一个孩子,按2)处 理删除最大元素 Status Delete BST(BiTree &T,KeyType kval) ·二叉查找树的平均查找长度 p (n)=2 (n+1)/n *logn+C 二叉平衡(查找)树 - 树中每个结点的左、右子树深度之差的绝对值不大 于1,这种平衡状态的二叉查找树。实现方法:平 衡旋转技术 ypb@ustc.edu.cn 10 中国科学技术大学
ypb@ustc.edu.cn 10 中国科学技术大学 • 删除结点的处理方法 1)若是叶子结点,直接删除 2)只有一个孩子,则将其孩子直接挂到其双亲上。 3)有两个孩子,找左孩子中最大的一个元素,代替被 删除结点,最大元素肯定只有一个孩子,按2)处 理删除最大元素 – Status Delete_BST(BiTree &T, KeyType kval) • 二叉查找树的平均查找长度 p(n)=2(n+1)/n *logn+C • 二叉平衡(查找)树 – 树中每个结点的左、右子树深度之差的绝对值不大 于1,这种平衡状态的二叉查找树。实现方法:平 衡旋转技术