
Constraint Satisfaction Problems 吉建民 USTC jianminQustc.edu.cn 2022年3月21日 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint Satisfaction Problems 吉建民 USTC jianmin@ustc.edu.cn 2022 年 3 月 21 日

Used Materials Disclaimer:本课件采用了S.Russell and P.Norvig's Artificial Intelligence-A modern approach slides,徐林莉老师课件和其他网 络课程课件,也采用了GitHub中开源代码,以及部分网络博客 内容 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Used Materials Disclaimer: 本课件采用了 S. Russell and P. Norvig’s Artificial Intelligence –A modern approach slides, 徐林莉老师课件和其他网 络课程课件,也采用了 GitHub 中开源代码,以及部分网络博客 内容

课程回顾 Best-first search Heuristic functions estimate costs of shortest paths Good heuristics can dramatically reduce search cost Greedy best-first search expands lowest h incomplete and not always optimal A*search expands lowest g+h complete and optimal also optimally efficient(up to tie-breaks,for forward search) Admissible heuristics can be derived from exact solution of relaxed problems 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 课程回顾 Best-first search ▶ Heuristic functions estimate costs of shortest paths ▶ Good heuristics can dramatically reduce search cost ▶ Greedy best-first search expands lowest h ▶ incomplete and not always optimal ▶ A* search expands lowest g + h ▶ complete and optimal ▶ also optimally efficient (up to tie-breaks, for forward search) ▶ Admissible heuristics can be derived from exact solution of relaxed problems

课程回顾 Local search algorithms the path to the goal is irrelevant;the goal state itself is the solution keep a single "current"state,try to improve it Hill-climbing search depending on initial state,can get stuck in local maxima Simulated annealing search escape local maxima by allowing some "bad"moves but gradually decrease their frequency Local beam search Keep track of k states rather than just one Genetic algorithms 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 课程回顾 Local search algorithms ▶ the path to the goal is irrelevant; the goal state itself is the solution ▶ keep a single “current” state, try to improve it ▶ Hill-climbing search ▶ depending on initial state, can get stuck in local maxima ▶ Simulated annealing search ▶ escape local maxima by allowing some “bad” moves but gradually decrease their frequency ▶ Local beam search ▶ Keep track of k states rather than just one ▶ Genetic algorithms

Table of Contents CSP examples Backtracking search for CSPs Problem structure and problem decomposition Local search for CSPs 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Table of Contents CSP examples Backtracking search for CSPs Problem structure and problem decomposition Local search for CSPs

Constraint satisfaction problems(CSPs) Standard search problem: state is a "black box"-any old data structure that supports goal test,eval,successor 任何可以由目标测试、评价函数、后继函数访问的数据结构 CSP: state is defined by Xi with values from domain (Di goal test is a set of constraints specifying allowable combinations of values for subsets of variables 每个约束包括一些变量的子集,并指定这些子集的值之间允 许进行的合并 Simple example of a formal representation language(形式化 表示方法) ~Allows useful general-purpose(通用的,而不是问题特定 algorithms with more power than standard search algorithms 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) ▶ Standard search problem: ▶ state is a “black box” –– any old data structure that supports goal test, eval, successor 任何可以由目标测试、评价函数、后继函数访问的数据结构 ▶ CSP: ▶ state is defined by Xi with values from domain(值域) Di ▶ goal test is a set of constraints specifying allowable combinations of values for subsets of variables 每个约束包括一些变量的子集,并指定这些子集的值之间允 许进行的合并 ▶ Simple example of a formal representation language (形式化 表示方法) ▶ Allows useful general-purpose (通用的,而不是问题特定 的) algorithms with more power than standard search algorithms

Constraint satisfaction problems(CSPs) A constraint satisfaction problem(CSP)consists of three components,&D,and C: is a set of variables,{X1,...,Xn} D is a set of domains,[D1,...,Dn},one for each variable Each domain D;consists of a set of allowable values, [v1,...,vk}for variable Xi. C is a set of constraints that specify allowable combinations of values Each constraint Ci consists of a pair(scope,rel,where scope is a tuple of variables that participate in the constraint and rel is a relation that defines the values that those variables can take on A relation can be represented as an explicit list of all tuples of values that satisfy the constraint,or as an abstract relation that supports two operations:testing if a tuple is a member of the relation and enumerating the members of the relation 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) A constraint satisfaction problem (CSP) consists of three components, X , D, and C: ▶ X is a set of variables, {X1, . . . , Xn} ▶ D is a set of domains, {D1, . . . , Dn}, one for each variable ▶ Each domain Di consists of a set of allowable values, {v1, . . . , vk} for variable Xi . ▶ C is a set of constraints that specify allowable combinations of values ▶ Each constraint Ci consists of a pair ⟨scope,rel⟩, where scope is a tuple of variables that participate in the constraint and rel is a relation that defines the values that those variables can take on ▶ A relation can be represented as an explicit list of all tuples of values that satisfy the constraint, or as an abstract relation that supports two operations: testing if a tuple is a member of the relation and enumerating the members of the relation

Constraint satisfaction problems(CSPs) To solve a CSP,we need to define a state space and the notion of a solution Each state in a CSP is defined by an assignment of values to some or all of the variables,Xi=vi,Xj=vj,... An assignment that does not violate any constraints is called a consistent or legal assignment A complete assignment is one in which every variable is assigned A partial assignment is one that assigns values to only some of the variables A solution to a CSP is a consistent,complete assignment 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) To solve a CSP, we need to define a state space and the notion of a solution ▶ Each state in a CSP is defined by an assignment of values to some or all of the variables, {Xi = vi , Xj = vj , . . .} ▶ An assignment that does not violate any constraints is called a consistent or legal assignment ▶ A complete assignment is one in which every variable is assigned ▶ A partial assignment is one that assigns values to only some of the variables ▶ A solution to a CSP is a consistent, complete assignment
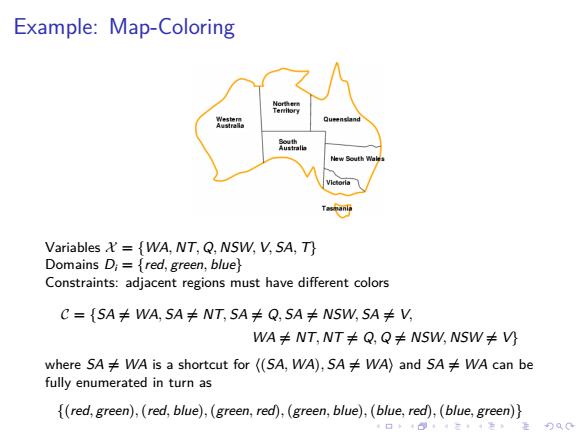
Example:Map-Coloring unne Variables={WA,NT,Q,NSW,V,SA,T} Domains D;=red,green,blue Constraints:adjacent regions must have different colors C={SA≠WA,5A≠NT,SA≠Q,5A≠NSW,SA≠V, WA≠NT,NT≠Q,Q≠NSw,NSW≠ where SA≠WA is a shortcut for(SA,WA),SA≠WA)and SA≠WA can be fully enumerated in turn as (red,green),(red,blue),(green,red),(green,blue),(blue,red),(blue,green)) 2ac
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Map-Coloring Variables X = {WA, NT, Q, NSW, V, SA, T} Domains Di = {red, green, blue} Constraints: adjacent regions must have different colors C = {SA ̸= WA, SA ̸= NT, SA ̸= Q, SA ̸= NSW, SA ̸= V, WA ̸= NT, NT ̸= Q, Q ̸= NSW, NSW ̸= V} where SA ̸= WA is a shortcut for ⟨(SA, WA), SA ̸= WA⟩ and SA ̸= WA can be fully enumerated in turn as {(red, green),(red, blue),(green,red),(green, blue),(blue,red),(blue, green)}

Example:Map-Coloring Ta呼 Solutions are assignments satisfying all constraints,e.g., {WA=red,NT=green,Q=red,NSW=green,V=red, SA=blue,T=green} 口·三色,进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Map-Coloring Solutions are assignments satisfying all constraints, e.g., {WA = red, NT = green, Q = red, NSW = green, V = red, SA = blue,T = green}