
Logical Agents 吉建民 USTC jianminOustc.edu.cn 2022年4月5日 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logical Agents 吉建民 USTC jianmin@ustc.edu.cn 2022 年 4 月 5 日

Used Materials Disclaimer:本课件采用了S.Russell and P.Norvig's Artificial Intelligence-A modern approach slides,徐林莉老师课件和其他网 络课程课件,也采用了GitHub中开源代码,以及部分网络博客 内容 口卡4三4色进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Used Materials Disclaimer: 本课件采用了 S. Russell and P. Norvig’s Artificial Intelligence –A modern approach slides, 徐林莉老师课件和其他网 络课程课件,也采用了 GitHub 中开源代码,以及部分网络博客 内容

Some modeling paradigms State-based models:search problems,MDPs,games Applications:routing finding,game playing,etc. Think in terms of states,actions,and costs Variable-based models:CSPs,Bayesian networks Applications:scheduling,medical diagnosis,etc. Think in terms of variables and factors Logic-based models:propositional logic,first-order logic Applications:theorem proving,verification,reasoning Think in terms of logical formulas and inference rules Search problems Constraint satisfaction problems Markov decision processes Markov networks Adversarial games Bayesian networks Reflex States Variables "Low-level intelligence' "High-level intelligence Machine learning
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Some modeling paradigms ▶ State-based models: search problems, MDPs, games ▶ Applications: routing finding, game playing, etc. ▶ Think in terms of states, actions, and costs ▶ Variable-based models: CSPs, Bayesian networks ▶ Applications: scheduling, medical diagnosis, etc. ▶ Think in terms of variables and factors ▶ Logic-based models: propositional logic, first-order logic ▶ Applications: theorem proving, verification, reasoning ▶ Think in terms of logical formulas and inference rules

Example Question:If X1+X2 10 and X1-X2 =4,what is X1? Think about how you solved this problem.You could treat it as a CSP with variables Xi and X2,and search through the set of candidate solutions,checking the constraints. However,more likely,you just added the two equations, divided both sides by 2 to easily find out that X1=7. This is the power of logical inference,where we apply a set of truth-preserving rules to arrive at the answer.This is in contrast to what is called model checking,which tries to directly find assignments. We'll see that logical inference allows you to perform very powerful manipulations in a very compact way.This allows us to vastly increase the representational power of our models. 口卡+四t4二老正)QG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example ▶ Question: If X1 + X2 = 10 and X1 − X2 = 4, what is X1? ▶ Think about how you solved this problem. You could treat it as a CSP with variables X1 and X2, and search through the set of candidate solutions, checking the constraints. ▶ However, more likely, you just added the two equations, divided both sides by 2 to easily find out that X1 = 7. ▶ This is the power of logical inference, where we apply a set of truth-preserving rules to arrive at the answer. This is in contrast to what is called model checking, which tries to directly find assignments. ▶ We’ll see that logical inference allows you to perform very powerful manipulations in a very compact way. This allows us to vastly increase the representational power of our models

A historical note Logic was dominant paradigm in Al before 1990s Problem 1:deterministic,didn't handle uncertainty (probability addresses this) Problem 2:rule-based,didn't allow fine tuning from data (machine learning addresses this) Strength:provides expressiveness in a compact way There is one strength of logic which has not quite yet been recouped by existing probability and machine learning methods,and that is expressivity of the model 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A historical note ▶ Logic was dominant paradigm in AI before 1990s ▶ Problem 1: deterministic, didn’t handle uncertainty (probability addresses this) ▶ Problem 2: rule-based, didn’t allow fine tuning from data (machine learning addresses this) ▶ Strength: provides expressiveness in a compact way ▶ There is one strength of logic which has not quite yet been recouped by existing probability and machine learning methods, and that is expressivity of the model

Motivation:smart personal assistant Tell information Ask questions Use natural language! How to build smart personal assistants? Systems like Apple's Siri,Microsoft Cortana,Amazon Echo (Alexa).and Google Now (Assistant) Smart speaker(current):Intent Detection Slot Filling Search Smart speaker(future):Semantic Parsing Reasoning Need to: Digest heterogenous information Reason deeply with that information
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Motivation: smart personal assistant ▶ How to build smart personal assistants? ▶ Systems like Apple’s Siri, Microsoft Cortana, Amazon Echo (Alexa), and Google Now (Assistant) ▶ Smart speaker (current): Intent Detection + Slot Filling + Search ▶ Smart speaker (future): Semantic Parsing + Reasoning ▶ Need to: ▶ Digest heterogenous information ▶ Reason deeply with that information

Language Language is a mechanism for expression Natural languages (informal): ·汉语:二能除偶数。 English:Two divides even numbers. Programming languages (formal): Python:def even(x):return x 2 ==0 C++:bool even(int x)return x 2 ==0; Logical languages (formal): First-order logic:Vx.Even(x)-Divides(x,2) 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Language ▶ Language is a mechanism for expression ▶ Natural languages (informal): ▶ 汉语:二能除偶数。 ▶ English: Two divides even numbers. ▶ Programming languages (formal): ▶ Python: def even(x): return x % 2 == 0 ▶ C++: bool even(int x) { return x % 2 == 0; } ▶ Logical languages (formal): ▶ First-order logic: ∀x. Even(x) → Divides(x, 2)

Two goals of logic Represent knowledge about the world Reason with that knowledge 口卡4三,4色,进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Two goals of logic

Elaboration Tolerance Elaboration Tolerance (McCarthy,1998) "A formalism is elaboration tolerant if]it is convenient to modify a set of facts expressed in the formalism to take into account new phenomena or changed circumstances." Uniform problem representation For solving a problem instance of a problem class C, I is represented as a set of facts P. C is represented as a set of rules Pc.and Pc can be used to solve all problem instances in C 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Elaboration Tolerance ▶ Elaboration Tolerance (McCarthy, 1998) “A formalism is elaboration tolerant [if] it is convenient to modify a set of facts expressed in the formalism to take into account new phenomena or changed circumstances.” ▶ Uniform problem representation For solving a problem instance I of a problem class C, ▶ I is represented as a set of facts PI , ▶ C is represented as a set of rules PC, and ▶ PC can be used to solve all problem instances in C
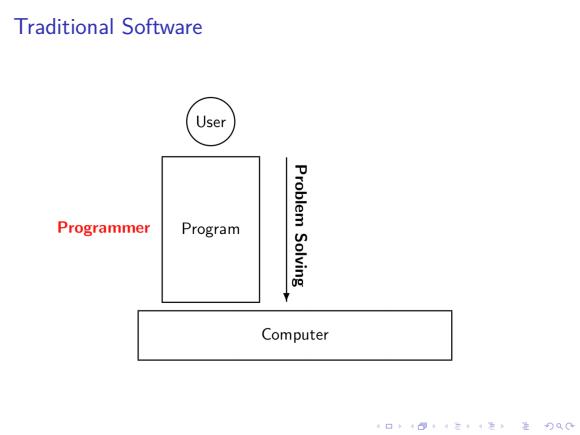
Traditional Software User Problem Programmer Program Solving Computer 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Traditional Software