
First-Order Logic Chapter 8
First-Order Logic Chapter 8

Outline ·Vhy FOL? Syntax and semantics of FOL ·Using FOL ·Vumpus world in FOL Knowledge engineering in FOL
Outline • Why FOL? • Syntax and semantics of FOL • Using FOL • Wumpus world in FOL • Knowledge engineering in FOL

Pros and cons of propositional logic Propositional logic is declarative Propositional logic allows partial/disjunctive/negated information -(unlike most data structures and databases) Propositional logic is compositional: © -meaning of B1.1A P12 is derived from meaning of B1.1 and of P1.2 Meaning in propositional logic is context-independent -(unlike natural language,where meaning depends on context) Propositional logic has very limited expressive power
Pros and cons of propositional logic ☺ Propositional logic is declarative ☺ Propositional logic allows partial/disjunctive/negated information – (unlike most data structures and databases) – ☺ Propositional logic is compositional: ☺ – meaning of B1,1 P1,2 is derived from meaning of B1,1 and of P1,2 – ☺ Meaning in propositional logic is context-independent – (unlike natural language, where meaning depends on context) – Propositional logic has very limited expressive power

First-order logic Whereas propositional logic assumes the world contains facts, first-order logic (like natural language) assumes the world contains ● -Objects:people,houses,numbers,colors, baseball games,wars,.. -Relations:red,round,prime,brother of, bigger than,part of,comes between,.. -Functions:father of,best friend,one more than nlue
First-order logic • Whereas propositional logic assumes the world contains facts, • first-order logic (like natural language) assumes the world contains • – Objects: people, houses, numbers, colors, baseball games, wars, … – – Relations: red, round, prime, brother of, bigger than, part of, comes between, … – Functions: father of, best friend, one more than, plus, …

Syntax of FOL:Basic elements ·Constants KingJohn,2,NUS,... ·Predicates Brother,>,.. 。Functions Sqrt,LeftLegof,... 。Variables X,y;a,b,... ·Connectives,→,入,V,→ ·Equality ·Quantifiers V,J
Syntax of FOL: Basic elements • Constants KingJohn, 2, NUS,... • Predicates Brother, >,... • Functions Sqrt, LeftLegOf,... • Variables x, y, a, b,... • Connectives , , , , • Equality = • Quantifiers ,

Atomic sentences Atomic sentence predicate (term,...,term) or term=term2 Term function (term,...,term) or constant or variable E.g.,Brother(KingJohn,RichardTheLionheart)> (Length(LeftLegOf(Richard)), Length(LeftLegOf(KingJohn)))
Atomic sentences Atomic sentence = predicate (term1 ,...,termn ) or term1 = term2 Term = function (term1 ,...,termn ) or constant or variable • E.g., Brother(KingJohn,RichardTheLionheart) > (Length(LeftLegOf(Richard)), Length(LeftLegOf(KingJohn)))

Complex sentences Complex sentences are made from atomic sentences using connectives S,S1ΛS2,S1VS2,S1→S2,S1台S2, E.g.Sibling(KingJohn,Richard) Sibling(Richard,KingJohn) >(1,2)V≤(1,2) >(1,2)Λ>(1,2)
Complex sentences • Complex sentences are made from atomic sentences using connectives • S, S1 S2 , S1 S2 , S1 S2 , S1 S2 , E.g. Sibling(KingJohn,Richard) Sibling(Richard,KingJohn) >(1,2) ≤ (1,2) >(1,2) >(1,2)

Truth in first-order logic Sentences are true with respect to a model and an interpretation Model contains objects(domain elements)and relations among them Interpretation specifies referents for constant symbols → objects predicate symbols → relations function symbols functional relations An atomic sentence predicate(termj,...,tem)is true iff the objects referred to by term,...,termn are in the relation referred to by predicate
Truth in first-order logic • Sentences are true with respect to a model and an interpretation • Model contains objects (domain elements) and relations among them • • Interpretation specifies referents for constant symbols → objects predicate symbols → relations function symbols → functional relations • An atomic sentence predicate(term1 ,...,termn ) is true iff the objects referred to by term1 ,...,termn are in the relation referred to by predicate
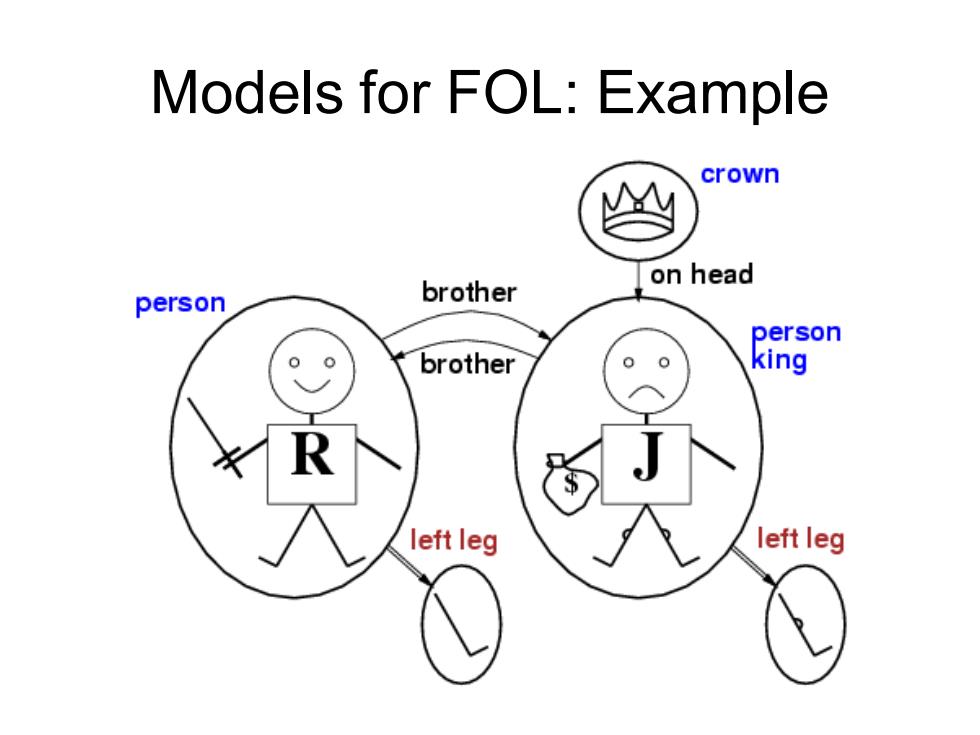
Models for FOL:Example crown on head person brother person brother king left leg left leg
Models for FOL: Example

Universal quantification V Everyone at NUS is smart: Vx At(X,NUS)Smart(x) Vx P is true in a model m iff P is true with x being each possible object in the model Roughly speaking,equivalent to the conjunction of instantiations of P At(KingJohn,NUS)Smart(KingJohn) At(Richard,NUS)=Smart(Richard)
Universal quantification • • Everyone at NUS is smart: x At(x,NUS) Smart(x) • x P is true in a model m iff P is true with x being each possible object in the model • • Roughly speaking, equivalent to the conjunction of instantiations of P • At(KingJohn,NUS) Smart(KingJohn) At(Richard,NUS) Smart(Richard) At(NUS,NUS) Smart(NUS)