
【8-I'PI d3 g-I'五HLdVHO SHHOMLHN NVISHAV
orks netw yesian Ba 14.1–3 Chapter 1 14.1–3 Chapter

石8-I'PI dD suolnquas!pp9zμooweled◇ SI4 uewaS◇ xenuKS◇ ourino
Outline Syntax ♦ Semantics ♦ distributions rameterized aP ♦ 2 14.1–3 Chapter

-I'PI d3 sanjen quaued jo uoneuiqwoo ypea joj'X Jano uolinquis!p ay 3un!(d)aqe Au!qeqoud jeuon!puo e se paquaseda uonnqunsip jeuon!puoo 'aseo nsejdwis ay ul ((xsquad xd :squaued shl uanI apou ypea joj uoinquasip leuoll!puoo e (saouanjju!1paP,≈u)4de83 !poe‘pp3pe eqeuen Jad auo 'sapou o nas e :xequ/S suonnq!as!p quiof llny jo uoneoyipads aedwo Joy aouay pue suolasse aouapuadapul jeuon!puoo joj uonenou jeolyde8 'ajdwls y SyIoMou ueisakeg
orks w net esian y Ba assertions endence indep conditional r fo notation graphical simple, A distributions joint full of ecification sp compact r fo hence and Syntax: riable va er p one des, no of set a influences”) “directly ≈ (link graph acyclic directed, a rents: pa its given de no each r fo distribution conditional a )) i X( ents ar P|i X( P as resented rep distribution conditional case, simplest the In the giving (CPT) table y robabilit p conditional a values rent pa of combination each r fo i X over distribution 3 14.1–3 Chapter

8-I'PI anduyD figzaD uanI quapuadapul Klleuon!puo aue y5100 pue ayo0ygooI sa]qeuen Jayno ayn jo quapuadapu!s!1ayaDa M yoje eyoeyooL 人4neO JayeaM :suo!asse aouapuadapu!leuo!!puo sapooua oMau jo 3oodoL aldwexH
Example assertions: endence indep conditional des enco rk ow net of ology op T Weather Cavity Catch Toothache riables va other the of endent indep is eather W ity av C given endent indep conditionally re a atch C and oothache T 4 14.1–3 Chapter

g8-I'VI duo lle on uyor asneo ueo wjeje ay- lle on Kew asneo ueo wJeje ay_- yo weje ayn ias ueo ayenbyuea uy- go wJeje ayn ias ues jejgunq y- :pajMouy .Jesne,,s3 KBolodo oM3N s11D,.lDN‘s1D,Ou40‘u.lDH‘3 yonby?lDg‘o16.lmg:so19eeΛ je3nq e aay sl 'sayenbyuea joulw Kq yo 1as s,sawnawos 'le 1,usaop Kiew uoqyBiau inq 'guiguu s!weje Kw Kes o1 slleo uyor joqyBiau 'yom ie w,l oduexH
Example r o neighb but ringing, is rm ala my y sa to calls John r o neighb rk, ow at I’m a there Is es. rthquak ea r mino yb off set it’s Sometimes call. esn’t do ry Ma r? burgla sl al Cy ar M, sl al ohnC J, mar Al , e uak thq ar E, ar l g ur B riables: aV wledge: kno “causal” reflects ology top rk ow Net off rm ala the set can r burgla A– off rm ala the set can e rthquak ea An – call to ry Ma cause can rm ala The – call to John cause can rm ala The – 5 14.1–3 Chapter
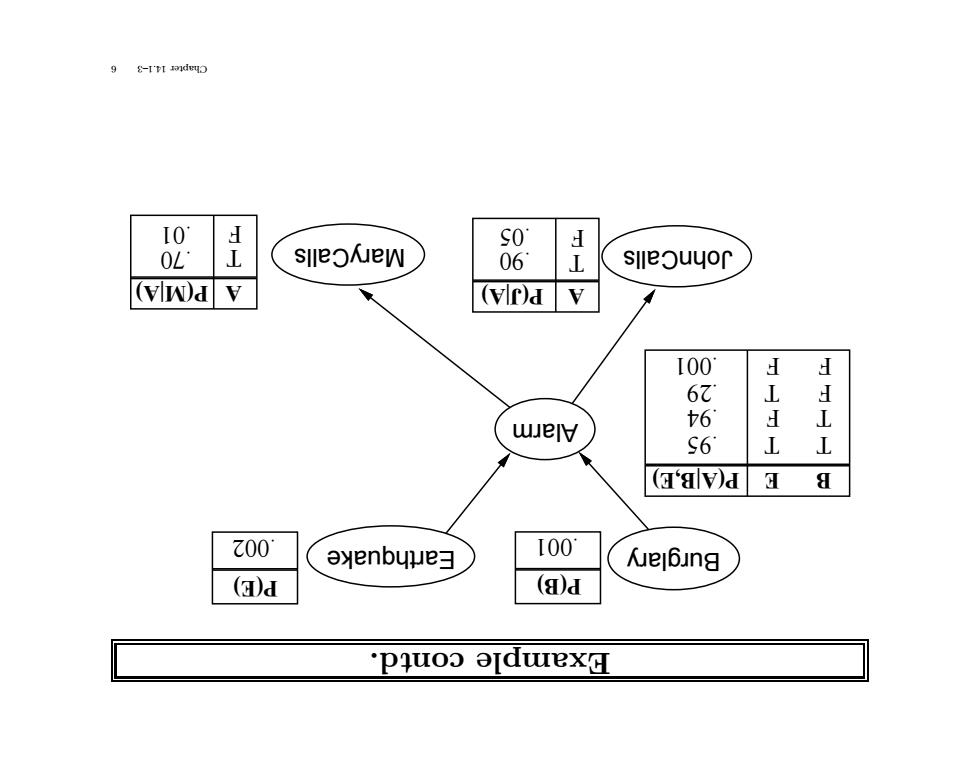
9 $-I'I anduD IO SO OL slleoeW 06 L slleouyor (vw)dv (vIr)av [00 d d 67 L d 6 wely L s6 L L (alvda a Z00 ayenbμe] I00 人ue6na (3a (aJ pquoo aldwexH
td. con Example .001 P(B) .002 P(E) Alarm Earthquake MaryCalls JohnCalls Burglary B T T F F E T F T F .95 .29 .001 .94 P(A|B,E) A T F .90 .05 A P(J|A) T F .70 .01 P(M|A) 6 14.1–3 Chapter
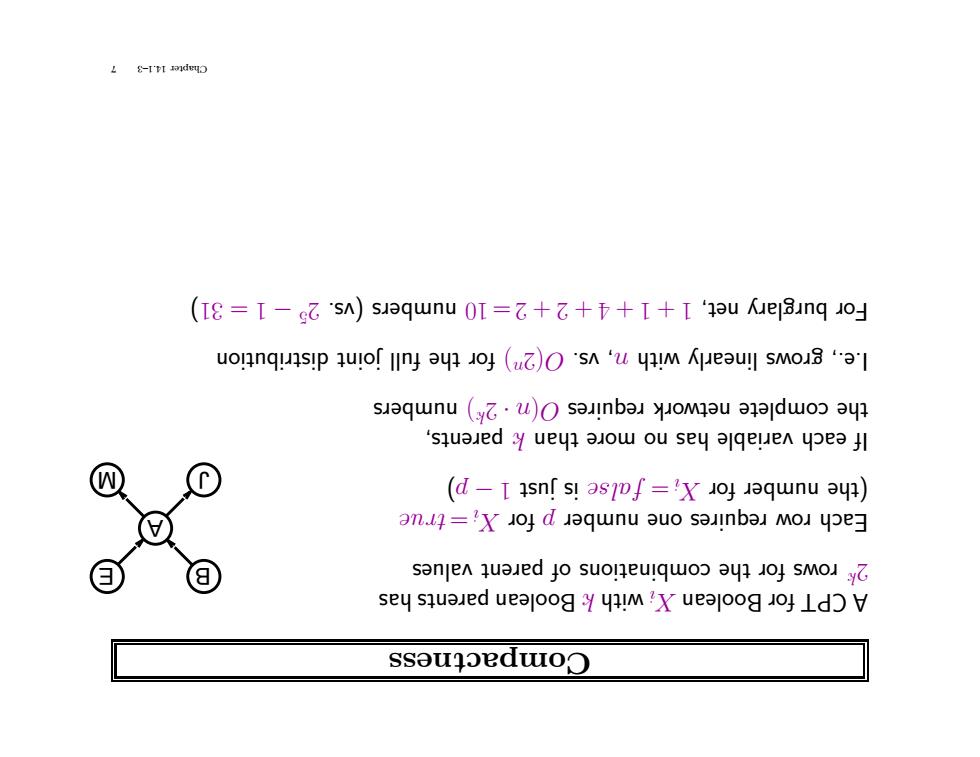
上8-I'PI d3 (I8=I-gZsA)sjeqwnu0I=乙+乙+币+I+I'au Ke]3unq Jo」 uonnquas!p quof lIng ayn oj 'sA 'u yim Kjeau!l sMo3 "l s3qunu(y乙·u)Os31nb31Ho4au341duoa44 'squaued y ueyn ajow ou sey ajqeuen yoea Jl (d-I isnf s!as of='x joj jaqwnu ay) an.l='x oj d jaqwnu auo sauinba mou ype S3 njen qualed0suoI4 eulqwo)∂y1 o]SMO1.y乙 sey squaed ueajoog y ylm'X ueajoog oj Ld)y ssouyoedwoD
Compactness has rents pa olean Bo k with i X olean Bo r fo CPT A E B J A M 2k values rent pa of combinations the r fo ws ro ue tr =i Xr fo p er numb one requires wro Each ) p −1 just is se al f =i Xr fo er numb (the rents, pa k than re mo no has riable va each If 2· n( O requires rk ow net complete the k ers numb ) (2 O vs. , n with rly linea ws gro I.e., n distribution joint full the r fo ) 2 (vs. ers numb 10 =2 +2 +4 +1 +1 net, ry burgla r oF −5 ) 31 =1 7 14.1–3 Chapter
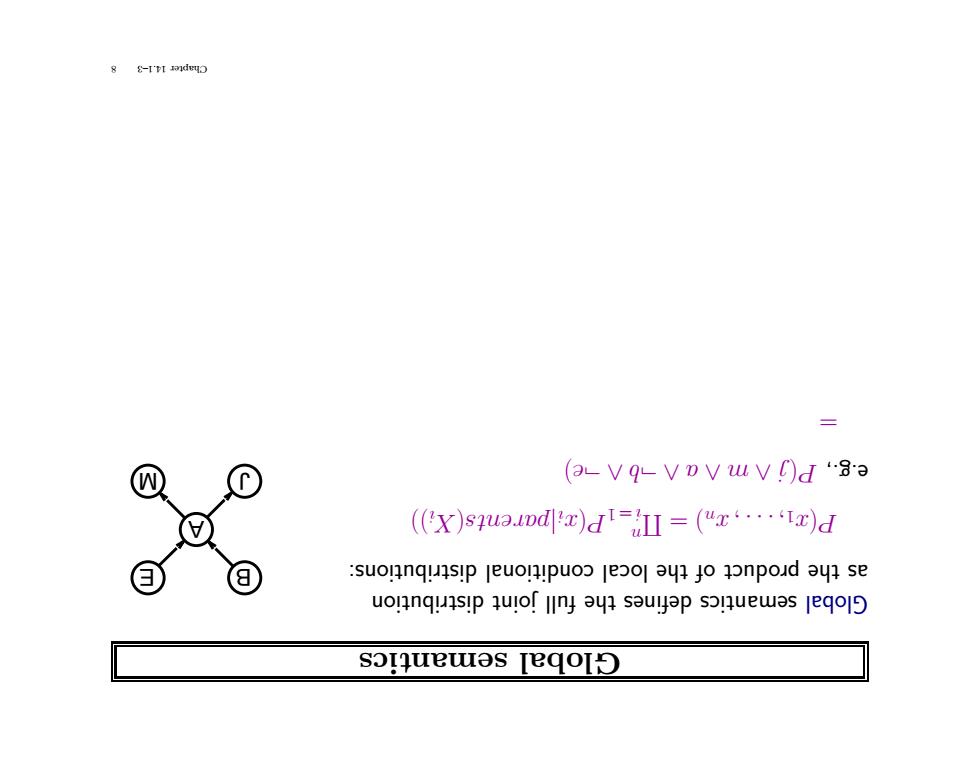
8 $-I'I anduyD = (aVq-vovwvr)da ((x)squaud)d=(ux)d :suolinq!sip jeuon!puoo jeool ay1 jo aonpod ayn se uolnqunsip quiof lIny ayn sauyap soluewas leqo]5 sorquewas jeqol
tics seman Global distribution joint full the defines semantics Global E B J A M distributions: conditional cal lo the of duct ro p the as Π =)n x, . . . , 1 x( P n P1 =i )) i X( ents par |i x( )e ¬ ∧b ¬ ∧a ∧ m∧j( P e.g., = 8 14.1–3 Chapter
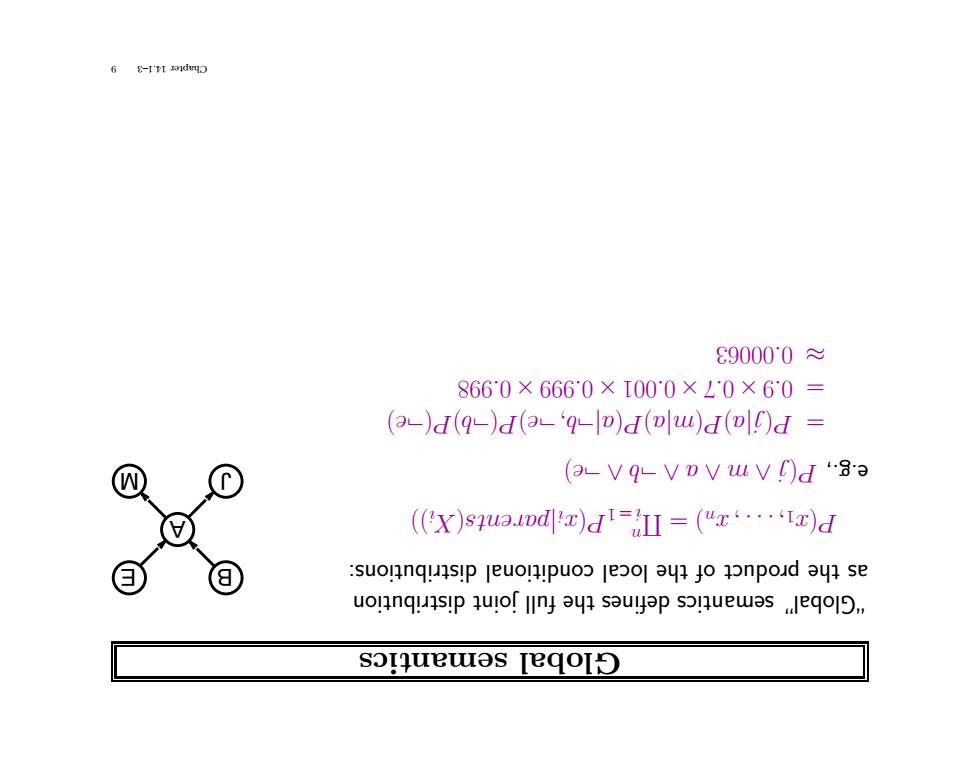
6 8-1'VI 890000≈ 8660×6660×I000×ㄥ0×60= (3)d(q-)d(aq-)d(w)d(!)d (a-Vq-vovwv)d "83 ((x)squaud)d==(")d :suolnq!sip leuon!puoo jeool ay]yo aonpoud ayl se uolnqunsip quiof lny ay sauyap sonuewas eqo]9, somquewas [eqol
tics seman Global distribution joint full the defines semantics “Global” E B J A M distributions: conditional cal lo the of duct ro p the as Π =)n x, . . . , 1 x( P n P1 =i )) i X( ents par |i x( )e ¬ ∧b ¬ ∧a ∧ m∧j( P e.g., )e ¬( P)b ¬( P)e ¬ b, |¬a( P) a| m( P) a| j( P = 998 . 0 × 999 . 0 × 001 . 0 ×7. 0 ×9. 0 = 00063 . 0 ≈ 9 14.1–3 Chapter
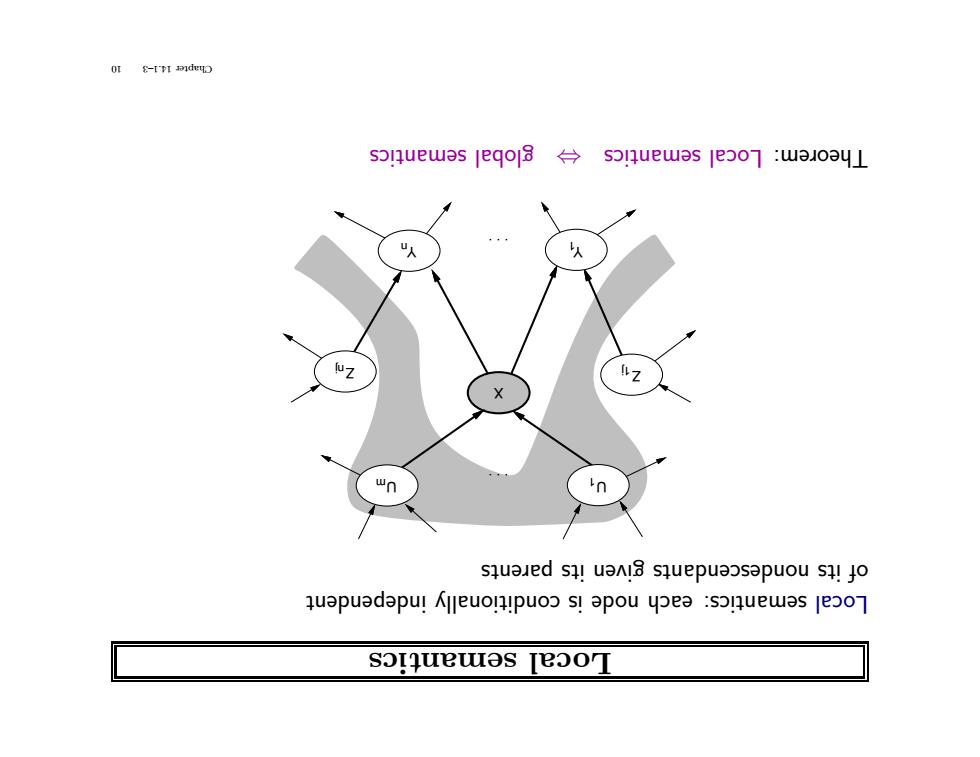
0I名-I'PI deD sonuewas eqo3 sonuewas jeo]:wajoay squaed sil uanlg squepuaosapuou si!jo quapuadapul Kjleuonlpuoo sl apou yoea soIuewas e5o] sorquewas jeoor
tics seman cal Lo endent indep conditionally is de no each semantics: cal Lo rents pa its given nondescendants its of . . . . . . 1 U X mU nY nj Z 1Y 1j Z semantics global ⇔ semantics cal Lo rem: Theo 10 14.1–3 Chapter