
【p-esom9 s'do 五-SNOILOHS‘五HHLdVHO SWHLIHOSTV HOHVHS IVOOT
algorithms ch sear Local 3–4 Sections 4, Chapter 1 3–4 Sections 4, Chapter
乙-tso9stmO (1μq人ua)s3 eds snonu!4uo)uI4 oueas jeoo7◇ (K9μq)swylo1eIn3u39◇ auIe3uuep34 ejnwlS◇ Suiqwip-HH◇ au!inO
Outline Hill-climbing ♦ annealing Simulated ♦ riefly) (b rithms algo Genetic ♦ riefly) b (very spaces continuous in rch sea cal Lo ♦ 2 3–4 Sections 4, Chapter

8 suonos'p ype3 s aulygo se Il3Mse∂ujuo oj∂1qe!ns‘3eds1 ue]suo 1 anoudw!on 'anens quauno,aBuis e daay :swylloe quawanodwl anneJanl asn ueo 'saseo yons ul alqeawn'squlensuo 3usies uoneunyuo puy o dSL 'uonein3yuo Tewrado puy :suoneinyuoadwo,,o as =aoeds aens uayL uolinjos ayl si gjasl!anens jeog ay :quena s!yed 'swalqod uoneziwndo Kuew ul swqqlIoSe quowanoidwr aalqeoI
algorithms t emen v impro e Iterativ irrelevant; is path roblems, p optimization many In solution the is itself state goal the configurations; “complete” of set = space state Then TSP e.g., configuration, optimal find timetable e.g., constraints, satisfying configuration find r, o rithms; algo rovement imp iterative use can cases, such In it rove imp to try state, “current” single a eep k rch sea offline as ell w as online r fo suitable space, Constant 3 3–4 Sections 4, Chapter
)-全so9 S'dmo sallo jo spues -noy yim Kpyinb Ken jewndo jo %I u!ylm 1 ypeoidde sy Jo squeue seBueyoxa asiMled wJojad 'non aajdwoo Kue yhIM jens walqoId uosIadsoles SurlleneIL :oldwexH
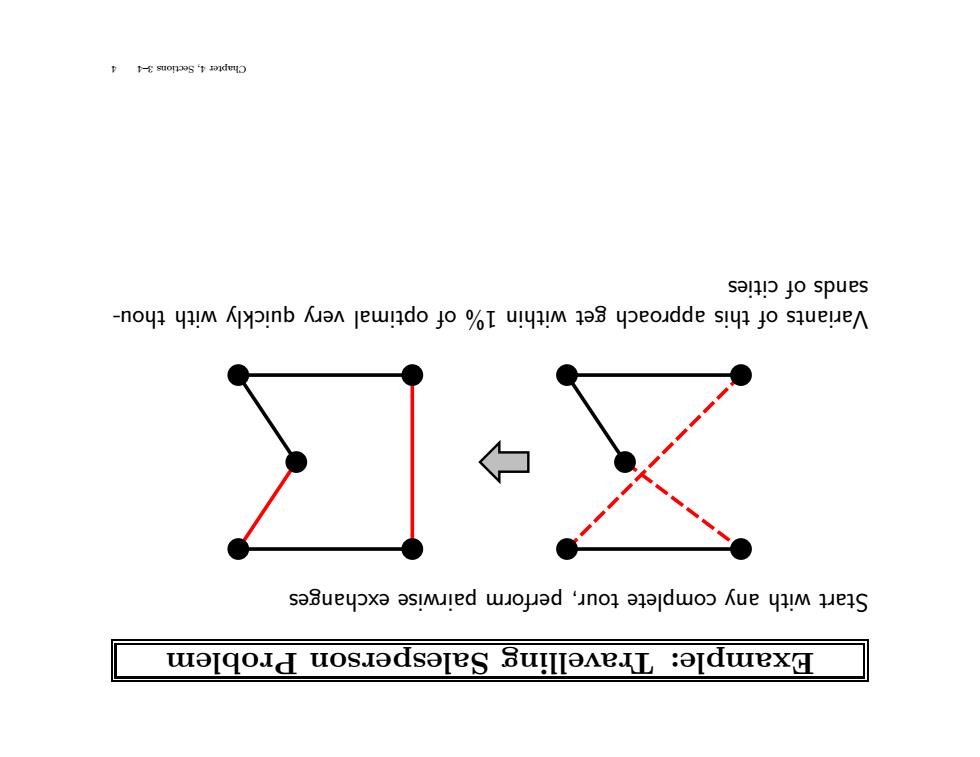
Problem erson Salesp elling v ra T Example: exchanges pairwise rm erfo p tour, complete any with rt Sta thou- with quickly very optimal of 1% within get roach app this of riants aV cities of sands 4 3–4 Sections 4, Chapter
g suonos't uonpput=u "8e 'u e Kon 10 Kjsnoauenuensul asowje swajqod suaanb-u sanjos sKemje nsowly 0=4 Z=4 9=4 不 不 不 不 不 不 不 sipIHuoo o Jaqunu aonpal on uaanb e anoW leuoelp o 'uwnjoo 'Mo awes ayi uo suaanb om ou yhm pueoq u x u ue uo suaanb u ind suoonb-u :oldwexH
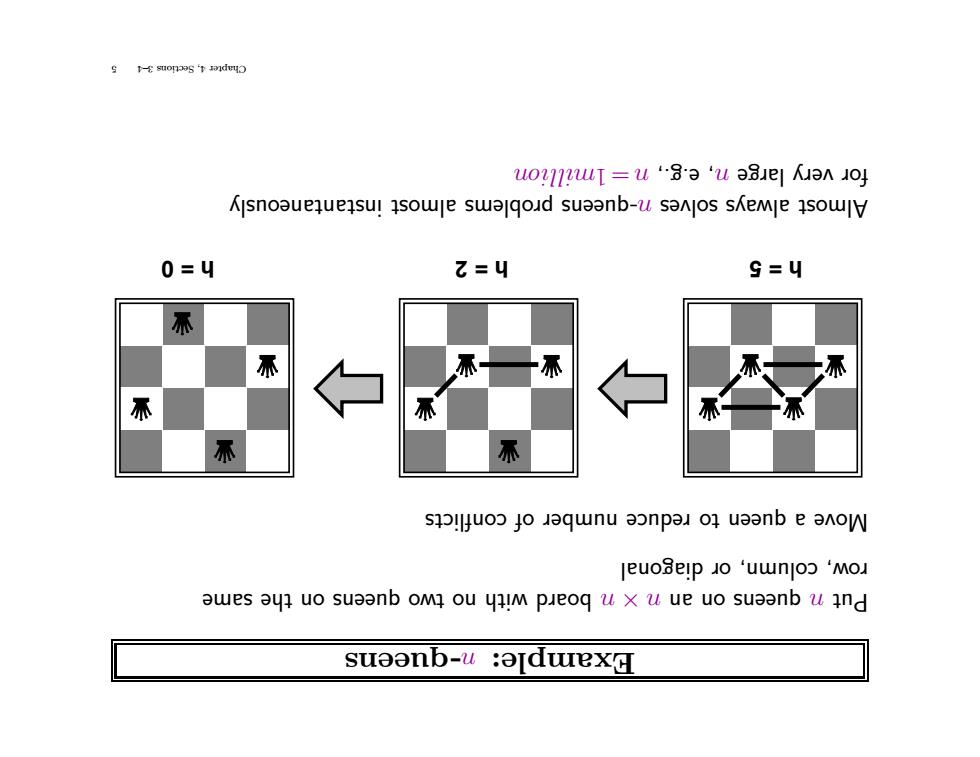
-queens n Example: same the on queens owt no with rd oa b n ×n an on queens n Put diagonal r o column, w, ro conflicts of er numb reduce to queen a Move h = 0 h = 2 h = 5 instantaneously almost roblems p -queens n solves ys a alw Almost ion l mil 1 =n e.g., , n rge la very r fo 5 3–4 Sections 4, Chapter

9£5uo195tmdO pua 0qy6au→7 ua.Lm3 uaLino]aLVIS uIngoI uoy huaun]anIVA>[oqy3!au]anIVA J! qua.Lino jo jossaoons panjen-1sayly e-ogybiau op dooL (Juangoid]aLVIS-IVILINI)CON-VW-UaLLno apou e ogybrau apou e 'qualino :salqerleA leool waqod e 'waqold :sandur wnwixew jeol e s!neyn aens e sumgoI (wapqold)SNIaNITO-TTIH uongounj .eIs3uue4HM8 o3 xo144uI1s3agu1quIp3X门, quoosop/quaose queipeI8 Io) 3uqw!-II!H
t) t/descen ascen t gradien (or bing Hill-clim amnesia” with fog thick in Everest climbing e “Lik maximum cal lo a is that state a returns ) oblem pr ( Hill-Climbing function roblem p a, oblem pr : inputs de no a , ent curr : ariables v cal lo de no a, or neighb ]) oblem pr [ te a Initial-St ( Make-Node ← ent curr do op lo ent curr of r successo highest-valued a ←or neighb ] ent curr [ te a St return then [current] alue V ≤r] o [neighb alue V if or neighb ← ent curr end 6 3–4 Sections 4, Chapter

L suopos't ewixew ey uo doo sapinoys woy ades sanow shemap!s wopuey adwo Klle-ewixew leol sawoJ3no 3uIqw!p !y Jesa-wopuey 01e1s juejjno eoeds ejejs wnwlxew leool .e.. wnwlxew jeool Japinoys wnwixew leqo]B uonouny ehnoelqo adeospuel aoeds anens Japisuoo o1 Injasn pquo 3urqw!-II!H
td. con bing Hill-clim e landscap space state consider to Useful current state objective function state space global maximum local maximum "flat" local maximum shoulder complete maxima—trivially cal lo overcomes climbing hill rt Random-resta maxima flat on op lo shoulders from e escap moves ys a sidew Random 7 3–4 Sections 4, Chapter

8-含so9StdD !qeqoid yim Ajuo prau-quaLn2 asTo 23u→?uam3uar90<☑VJ uaLino]anIVA-TOu]anTVA-V quaLino jo ossaoons palajas Kjwopuel e-yrau quaLino umngoI uay?0=I J! ]mp4ps→L opo04I→4IoJ (wa]qoid]LVLS-IVILINI)ON-VW-quaLin3 sdais puemumop jo 'qod 3ullouo neadwan e'L apou e xau apou e 'qualino :salqerreA Teool .aneadwan,,o1 awn woy Buiddew e amnpayos wajqoud e wangod :sandur aens uonnjos e suigoI (amnpayos 'wangoud )SNIIVaNNV-daLVInNIS uonoung Kouanba.y pue ozis noq]oseaop Allenpe3 inq sanow peq,,awos Suimolle Kq ewixew jeool adeosa :eap] Surleouue pazelnu!s
annealing ulated Sim moves “bad” some wing allo yb maxima cal lo e escap Idea: frequency and size their decrease gradually but state solution a returns ) dule sche oblem, pr ( ted-Annealing Simula function roblem p a, oblem pr : inputs erature” “temp to time from mapping a, dule sche de no a , ent curr : ariables v cal lo de no a, next steps rd a wnw do of rob. p controlling erature” “temp a , T ]) oblem pr [ te a Initial-St ( Make-Node ← ent curr do ∞ to 1 ←t for ]t[ dule sche ←T ent curr return then 0 = T if ent curr of r successo selected randomly a ← next ] ent curr [ alue V–] next [ alue V ←E∆ next ← ent curr then 0 > E∆ if e y robabilit p with only next ← ent curr else /T E ∆ 8 3–4 Sections 4, Chapter

6 suonos'p 198uInp3 yps aulμIe'noKel IS7∧u!p∂snp!M 3u!llepou ssaooud jesKyd o 'EG6T"Je sljodoW q pasin iuejen3 3unsaau ue Ajessaoau siys] I llews o I asneq x anens asaq ypeau sKemje ynoua KjMojs paseauap I 1=(x)d () uo4nqμ4 p uewz4Io9 saypea Kul!qeqoud uonednooo aens 'L aunejadwal,,paxy 1y Surleauue pazelnwrs Jo serqodoId
annealing ulated sim of erties Prop reaches y robabilit p ccupation o state , T erature” “temp fixed t A distribution Boltzman e α =) x( p ) x( E Tk x state est b reach ys a alw ⇒= enough wly slo decreased T ∗ e ecause b x( E ∗)/e Tk ) x( E e = Tk x( E ∗ ) x( E−) T small r fo 1 Tk ?? rantee gua interesting an rily necessa this Is delling mo cess ro p physical r fo 1953, al., et olis Metrop yb Devised etc. scheduling, airline out, y la VLSI in used Widely 9 3–4 Sections 4, Chapter

01-含so1p9S'pdgD juonoajas jeinieu o1 Kgojeue asojp ay1 anasqO sauo poog spueMon paselq 'juopue suossaoons asooyp :eapl ll!y jeo]awes uo dn pua saes y le 'uayo anb :walqold wayl uIof on saypueas jayho 1injal sanens poog puyy ieyl saypueas ilelleed u!un seypeas y se awes ay oN sJossaoons ayl lle jo y do]asooy 'I jo peensul salens daay :eapl yoleas weaq jeoor
h searc eam b cal Lo rs successo their all of k top ose cho 1; of instead states k eep k : Idea rallel! pa in run rches sea k as same the Not them join to rches sea other recruit states do go find that rches Sea hill cal lo same on up end states k all often, quite : Problem ones do go rds a wto biased , randomly rs successo k ose cho : Idea selection! natural to analogy close the Observe 10 3–4 Sections 4, Chapter