
I 9-I duyD S-五'五HLdVHO SHHOMLHN NVISHAV NI HONHHHINT
orks netw yesian Ba in Inference 14.4–5 Chapter 1 14.4–5 Chapter

oμeya4 uoW u!eyp AoyeW Kq3uau!1 ewIxoddv◇ uone nwls onseypons Kq aouaajul anewixoddy uoneulw!B∂I9 euen Kq3 ualajul 1ex3◇ uoneJawnua Kq aouajaju!ex ourino
Outline enumeration yb inference Exact ♦ elimination riable va yb inference Exact ♦ simulation chastic sto yb inference ximate ro App ♦ rlo Ca Monte chain ov rk Ma yb inference ximate ro App ♦ 2 14.4–5 Chapter

-I duyD jonow jauens Mau e paau op Kym :uoneuejdx ileasow aue sanjen Kqeqod yolym :sIsKjeue Ansuas Xaua∂so133upI34pI叫M:uoI1euou!03neA (aouapina'uoigon awooino)d oy paunbal aouelejul ons!!qeqoud :uonewjojul Kn apnpoul syuomnau uoisipap :suoisipap jewndO (=x)d(=)d==x)d :souanb announfuo) (asof=s1m1s 'uo=sqybvI'fdwa=a6nDDsDDoN)d" (=X)d leuew Joue sod andwo :sauanb adw!s sysel aouaojul
tasks Inference ) e = E|i X( P rginal ma r osterio p compute : queries Simple ) se al f = ts tar S on, = hts Lig , empty =e Gaug | oGas N( P e.g., ) e = E,i X|j X( P) e = E|i X( P =) e = E|j X,i X( P: queries Conjunctive rmation; info y utilit include rks ow net decision : decisions Optimal ) idence ev action, | outcome ( Pr fo required inference robabilistic p next? seek to evidence which : rmation info of alue V critical? most re a values y robabilit p which : analysis y Sensitivit r? moto rter sta new a need I do why : Explanation 3 14.4–5 Chapter

awn (up)O'aeds (u)O :uoneawnue asy-yndap anisiney (w)d()d(a'gl)d"(a)d (g)d= (olu)d(old(a‘alp)de)d(a)d〖o= (wtga :s3μuB⊥d)o npoud 3uisn s3μnu31 urof ing34μM3y (uo3a)d〖〖0= (u‘C‘a)d0= (u)d/(u‘f‘a)d= (u‘a)d :yHom4u人ue8nqy1uo人uanb1duIS uonequasada 1dxa sil unonsuo Ajlengpe inoyM qulof ay woy sajqeuen ino wns o3 Kem quauyS uoryelownua Aq oouolojul
umeration en yb Inference actually without joint the from riables va out sum to ya w intelligent Slightly resentation rep explicit its constructing rk: ow net ry burgla the on query Simple E B J A M ) mj, | B( P ) mj, ( /P ) mj, , B( P = ) mj, , B( Pα = ) mj, a, e, , B( Pa Σe Σα = entries: CPT of duct ro p using entries joint full Rewrite ) mj, | B( P ) a| m( P) a| j( P)e, B| a( P)e( P) B( Pa Σe Σα = ) a| m( P) a| j( P)e, B| a( Pa Σ)e( Pe Σ) B( Pα = d( O space, ) n( O enumeration: depth-first Recursive n time ) 4 14.4–5 Chapter

g-'I duy f=人4hMp9pu3X3as到33a4M ('(sia)Isad)v-alvuannNd x ((d )d umngo1 as1a ('(s.IDA)ISad)TIV-HLVHWNNG x (()d)d umngoI uoy uI fi anjen sey人JI (s.mn)LSHd→X O'I umgaI uaq?(s.ID0)ixLdNd J! Jaqwnu jeal e sumngol (o's.iDa)TIV-aLvHaNnNG uongoung ((X)6)aZIIVWHON uIn351 (uq]SHVA)TIV-aIVHaNON-()6 X oy anjen yim a puaixe op X jo 'x anjen yoea ioJ Aadwa Allenu!'X Jano uonnquasip e(X)6 天∩C∩{X}s319euen4HMHo4 u ueis3 Keg e 'uq d sajqeuen joy sanjen panasqo alqeuen Kanb ay 'x :sandur X Jno uoninq!sip e sumnga.I (ug''X)ySV-NOILVHNnNG uoIouny wyz!loSfe uorelownuH
algorithm umeration En X over distribution a returns ) bn , e, X( tion-Ask Enumera function riable va query the , X: inputs E riables va r fo values observed , e Y ∪ E ∪ } X{ riables va with rk ow net esian y Ba a , bn y empt initially , X over distribution a ←) X( Q do X of i x value h eac for Xr fo i x value with e extend ) e ], bn [ ars V( te-All Enumera ←)i x( Q )) X( Q( Normalize return er numb real a returns ) e, vars ( te-All Enumera function 1.0 return then ) vars ( Empty? if ) vars ( First ←Y e in y value has Y if ) e ), vars ( Rest ( te-All Enumera × )) Y( a P| y( P return then return else P )y e ), vars ( Rest ( te-All Enumera × )) Y( a P| y( P y y = Y with extended e is y e where 5 14.4–5 Chapter
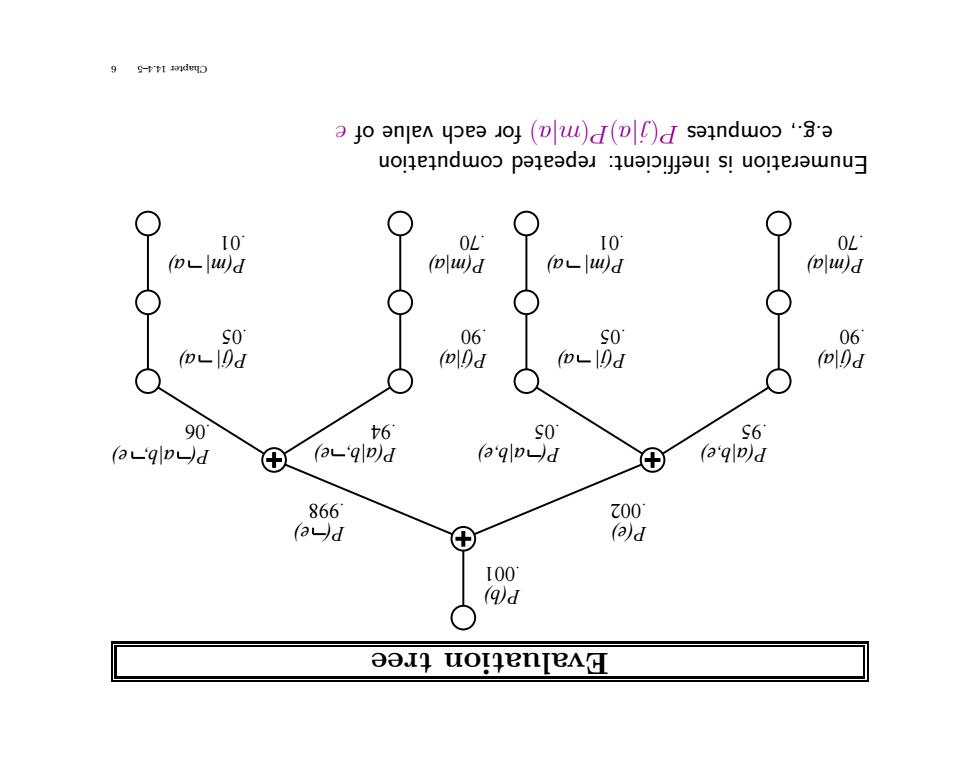
9 9-PPI a jo anjen ypea oj (w)d(D)d saindwo a uoneindwo paleadal :qualpiyaul si uonejawnu 10 OL IO OL oLl四d (ol四d (oLl四d (ou叫d SO 06 SO 06 DL9d Dd Ld ol9d Q 90 6 SO S6 (aLqloud (aL'ql)d a'qp→d ⊕ (a'ql)d 866 Z00 (aud ⊕ (a)d I00 Qd O a017 uorlenjeAH
tree aluation Ev P(j|a) .90 P(m|a) .01 .70 P(m| a) .05 P(j|a) P(j| a) .90 P(m|a) .01 .70 P(m| a) .05 P(j| a) P(b) .001 P(e) .002 P( e) .998 P(a|b,e) .06 .95 P( a|b, e) .05 P( a|b,e) .94 P(a|b, e) computation eated rep inefficient: is Enumeration e of value each r fo ) a| m( P) a| j( P computes e.g., 6 14.4–5 Chapter

L 9PI duD (q)NYr×(q)ao= (d ano wns)(q)nrYaf(g)do= (v ino wns)('q)wrYf(a)(g)do= (D)nf()rf(q')f()d(g)o= (o)wf(o)ff(a‘ap)d"☒(o)d☒(a)do= (o)mf(ol)d(3aD)d”☒e)dK(a)do= 8 (olu)d(ol)d(3‘alp)d☒(a)d(a)do= (u‘Cla)d uoleindwooa pIone o1 (siopej)sa]nsal azelpawaul Sulons 1aj-01-1y3u suonewwns ino Kue :uoneulwlja a]qeue uorzeurw!e alqerieA Aq aouolojul
elimination ariable v yb Inference right-to-left, summations out rry ca elimination: riable aV recomputation avoid to ) rs facto ( results intermediate ring sto ) mj, | B( P ) B( Pα = } {z | B )e( Pe Σ } {z | E )e, B| a( Pa Σ } {z | A ) a| j( P } {z | J ) a| m( P } {z | M ) a( Mf) a| j( P)e, B| a( Pa Σ)e( Pe Σ) B( Pα = ) a( Mf) a( J f)e, B| a( Pa Σ)e( Pe Σ) B( Pα = ) a( Mf) a( J f)e b, a, ( Afa Σ)e( Pe Σ) B( Pα = ) A out (sum )e b, ( MJ¯Af)e( Pe Σ) B( Pα = ) E out (sum )b( M ¯AJ ¯Ef) B( Pα = )b( M ¯AJ ¯Ef ×)b( Bfα = 7 14.4–5 Chapter

8 g-'PI duO (bqo)f=(bq)4×(9D)f:83 (Iz…Tzf.f..Ix)f= (1zTzf.f)对×(fTf5x…Tx) :f pue If soej jo npoud asIMqu!od X uo puadap aou op ff uiwnsse f×f×…×y=y×…×+y〖f×…×y=y×…×r区 sopey Bululewal jo onpod asiMquiod ul saouewqns dn ppe uolewwns ay]apisino sionpej quensuoo Kue anow :suonej jo ionpoud e wouy ajqeuen e ino gulwwns suorgelodo orseg :uoreuru!o olqeLie
erations op Basic elimination: ariable V rs: facto of duct ro p a from riable va a out Summing summation the outside rs facto constant any move rs facto remaining of duct ro p wise oint p in submatrices up add ¯ Xf ×i f ×· · · ×1 f =k f ×· · · × +1 i f x Σi f ×· · · ×1 f =k f ×· · · ×1 fx Σ X on end dep not do i f, . . . , 1 f assuming : 2 f and 1 f rs facto of duct ro p wise oint P )l z, . . . , 1 z, k y, . . . , 1 y(2 f ×)k y, . . . , 1 y, j x, . . . , 1 x(1 f )l z, . . . , 1 z, k y, . . . , 1 y, j x, . . . , 1 x( f = )c b, a, ( f =)c b, (2 f ×)b a, (1 f E.g., 8 14.4–5 Chapter

6 g-I duyD ((s10/)LondoHd-SIMLNIO)ZIIVNHON uIn30I (s.iogoof 'Da)Ino-wns-siogoof uou aqeuen uapply e s!ion J! [s0pDfl(白‘mn)HOLOVH-aMVW→slo4Df op son u son yoea ioj (uq]sHVA)asHaAay→slmn:[0→slo4D ("XX)d uonnqusip uo uds yomou jq e'uq quana ue se payloads aouapIna'a alqeuen Kanb ay'x :sandur X Jano uoninq!s!p e suInga.I(uq'a'X)SV-NOILVNINITH uonounJ wqqlloSte uoreurwe alqerle
algorithm elimination ariable V X over distribution a returns ) bn , e, X( tion-Ask Elimina function riable va query the , X: inputs event an as ecified sp evidence , e )n X, . . . , 1 X( P distribution joint ecifying sp rk ow net elief b a , bn ]) bn [ ars V( Reverse ← vars ;] [ ← factors do vars in var h eac for ] factors |) e, var ( ctor a Make-F [ ← factors ) factors , var ( Sum-Out ← factors then riable va hidden a is var if )) factors ( oduct Pointwise-Pr ( Normalize return 9 14.4–5 Chapter
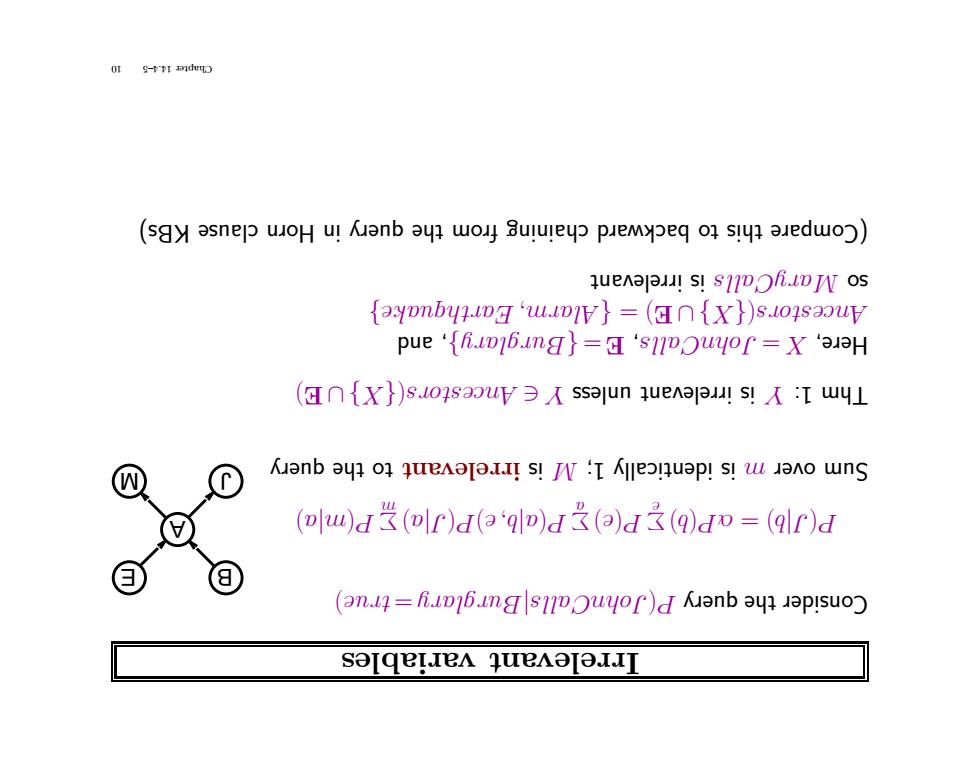
OI g-PI (sgy asne]woH u!Kanb ay woy 3ululeyp pemypeq o1 slya auedwo)) quenajaus!s1Dh.lDW os {3YDnb4?.lDa‘u.lDW}=(∩{X})s.04 saouy pue‘{i.lD16.uma}=‘s1DOu40r=X3H (C∩{X})s.04sa3uV3不ss3 jun que3 au s!天:Tw叫L 人uanb ayi o4 eAoJo.I.Is!JN‘I Klleonuap!s!u Jano wns (w)d(r)d(3'q)d()d(q)dv=(qlr)d (an.1=fI6.ing smouyor)d Kanb ayn Japisuo) salqelIeA queAOlaIIl
ariables v t an Irrelev ) ue tr =y ar l g ur B| sl al ohnC J( P query the Consider E B J A M )b( Pα =)b| J( P Xe )e( P Xa ) a| J( P)e b, | a( P Xm ) a| m( P query the to t an irrelev is M1; identically is m over Sum ) E∪} X{(s Ancestor ∈ Y unless irrelevant is Y 1: Thm and , }y ar l g ur B{ = E, sl al ohnC J = X Here, }e uak thq ar E m, ar Al { =) E∪} X{(s Ancestor irrelevant is sl al Cy ar M so KBs) clause rn Ho in query the from chaining rd a backw to this re (Compa 10 14.4–5 Chapter