
Semantics Syntax Bayesian networks CHAPTER 14.1- B AYESIAN NETWORK P(AB.E r can set the 目 Example ogy of network encodes conditional independence assertions Example 帼
Bayesian networks Chapter 14.1–3 Chapter 14.1–3 1 Outline ♦ Syntax ♦ Semantics ♦ Parameterized distributions Chapter 14.1–3 2 Bayesian networks A simple, graphical notation for conditional independence assertions and hence for compact specification of full joint distributions Syntax: a set of nodes, one per variable a directed, acyclic graph (link ≈ “directly influences”) a conditional distribution for each node given its parents: P(Xi |Parents(Xi)) In the simplest case, conditional distribution represented as a conditional probability table (CPT) giving the distribution over Xi for each combination of parent values Chapter 14.1–3 3 Example Topology of network encodes conditional independence assertions: Weather Cavity Toothache Catch Weather is independent of the other variables Toothache and Catch are conditionally independent given Cavity Chapter 14.1–3 4 Example I’m at work, neighbor John calls to say my alarm is ringing, but neighbor Mary doesn’t call. Sometimes it’s set off by minor earthquakes. Is there a burglar? Variables: Burglar, Earthquake, Alarm, JohnCalls, MaryCalls Network topology reflects “causal” knowledge: – A burglar can set the alarm off – An earthquake can set the alarm off – The alarm can cause Mary to call – The alarm can cause John to call Chapter 14.1–3 5 Example contd. .001 P(B) .002 P(E) Alarm Earthquake MaryCalls JohnCalls Burglary F F T T B F T F T E .001 .29 .94 .95 P(A|B,E) F T A .05 .90 P(J|A) F T A .01 .70 Chapter P(M|A) 14.1–3 6

-1X071018180046 e.g.PljAmAanA-e) Global semantics Global semantics For burglary net,++++2=10 numbers (vs.25-1 =31) glinearly()for the full joint distribution Compactness Q Q This chice of parents gurantees the: Constructing Bayesian networks Markoy blanket of its nondescendants given its paren Local semantics:each node is conditionally independen Local semantics P
Compactness A CPT for Boolean Xi with k Boolean parents has B E J A M 2 k rows for the combinations of parent values Each row requires one number p for Xi = true (the number for Xi = false is just 1 − p) If each variable has no more than k parents, the complete network requires O(n · 2 k ) numbers I.e., grows linearly with n, vs. O(2 n ) for the full joint distribution For burglary net, 1 + 1 + 4 + 2 + 2 = 10 numbers (vs. 2 5 − 1 = 31) Chapter 14.1–3 7 Global semantics Global semantics defines the full joint distribution B E J A M as the product of the local conditional distributions: P(x1, . . . , xn) = Πi n = 1P(xi |parents(Xi)) e.g., P(j ∧ m ∧ a ∧ ¬b ∧ ¬e) = Chapter 14.1–3 8 Global semantics “Global” semantics defines the full joint distribution B E J A M as the product of the local conditional distributions: P(x1, . . . , xn) = Πi n = 1P(xi |parents(Xi)) e.g., P(j ∧ m ∧ a ∧ ¬b ∧ ¬e) = P(j|a)P(m|a)P(a|¬b,¬e)P(¬b)P(¬e) = 0.9 × 0.7 × 0.001 × 0.999 × 0.998 ≈ 0.00063 Chapter 14.1–3 9 Local semantics Local semantics: each node is conditionally independent of its nondescendants given its parents . . . . . . U1 X Um Yn Znj Y1 Z1j Theorem: Local semantics ⇔ global semantics Chapter 14.1–3 10 Markov blanket Each node is conditionally independent of all others given its Markov blanket: parents + children + children’s parents . . . . . . U1 X Um Yn Znj Y1 Z1j Chapter 14.1–3 11 Constructing Bayesian networks Need a method such that a series of locally testable assertions of conditional independence guarantees the required global semantics 1. Choose an ordering of variables X1, . . . , Xn 2. For i = 1 to n add Xi to the network select parents from X1, . . . , Xi−1 such that P(Xi |Parents(Xi)) = P(Xi |X1, . . . , Xi−1) This choice of parents guarantees the global semantics: P(X1, . . . , Xn) = Πi n = 1P(Xi |X1, . . . , Xi−1) (chain rule) = Πi n = 1P(Xi |Parents(Xi)) (by construction) Chapter 14.1–3 12
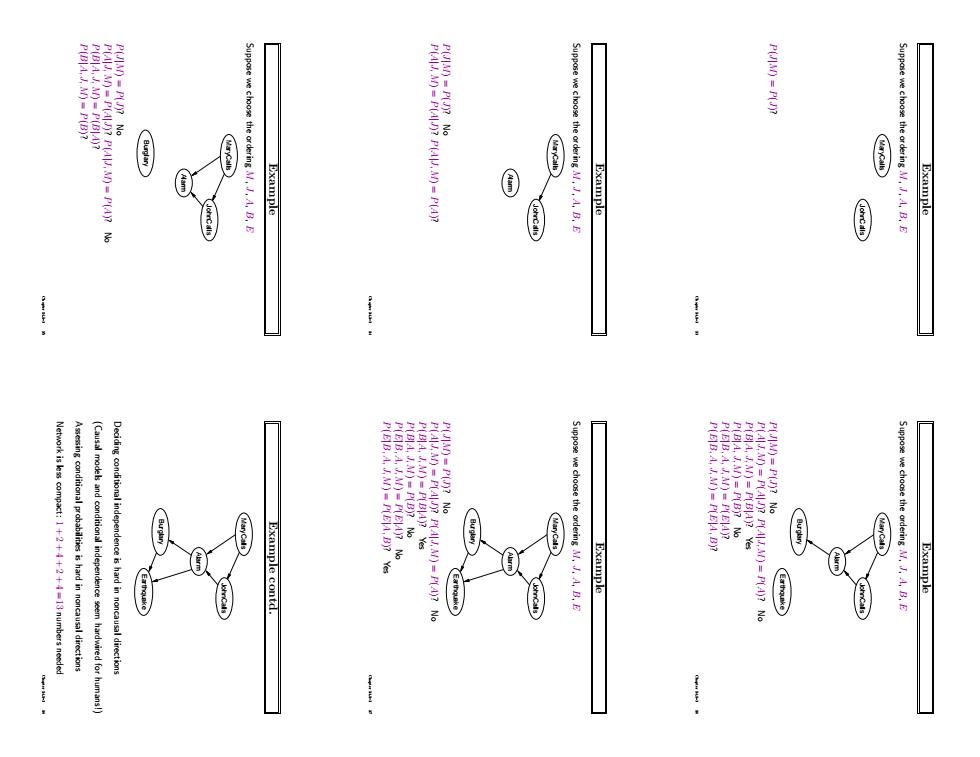
0 we choose the ordering M,A.B. uppase we choose the ordering ,A,B.E Example Network is kess compact:1+2+4+2+4-13 numbers neede Asingconditional probabilities is hard in noncausal directions (Causal models and conditiona independence seem hardwired for humans! Deciding conditional independence is hard in noncausal directions P(BA.J M)=P( Example contd we choose the ordering ,A, Example Suppose we choose the ordering A,.A,B.E Example 3R-3
Example Suppose we choose the ordering M, J, A, B, E MaryCalls JohnCalls P(J|M) = P(J)? Chapter 14.1–3 13 Example Suppose we choose the ordering M, J, A, B, E MaryCalls Alarm JohnCalls P(J|M) = P(J)? No P(A|J, M) = P(A|J)? P(A|J, M) = P(A)? Chapter 14.1–3 14 Example Suppose we choose the ordering M, J, A, B, E MaryCalls Alarm Burglary JohnCalls P(J|M) = P(J)? No P(A|J, M) = P(A|J)? P(A|J, M) = P(A)? No P(B|A, J, M) = P(B|A)? P(B|A, J, M) = P(B)? Chapter 14.1–3 15 Example Suppose we choose the ordering M, J, A, B, E MaryCalls Alarm Burglary Earthquake JohnCalls P(J|M) = P(J)? No P(A|J, M) = P(A|J)? P(A|J, M) = P(A)? No P(B|A, J, M) = P(B|A)? Yes P(B|A, J, M) = P(B)? No P(E|B, A, J, M) = P(E|A)? P(E|B, A, J, M) = P(E|A, B)? Chapter 14.1–3 16 Example Suppose we choose the ordering M, J, A, B, E MaryCalls Alarm Burglary Earthquake JohnCalls P(J|M) = P(J)? No P(A|J, M) = P(A|J)? P(A|J, M) = P(A)? No P(B|A, J, M) = P(B|A)? Yes P(B|A, J, M) = P(B)? No P(E|B, A, J, M) = P(E|A)? No P(E|B, A, J, M) = P(E|A, B)? Yes Chapter 14.1–3 17 Example contd. MaryCalls Alarm Burglary Earthquake JohnCalls Deciding conditional independence is hard in noncausal directions (Causal models and conditional independence seem hardwired for humans!) Assessing conditional probabilities is hard in noncausal directions Network is less compact: 1 + 2 + 4 + 2 + 4 = 13 numbers needed Chapter 14.1–3 18
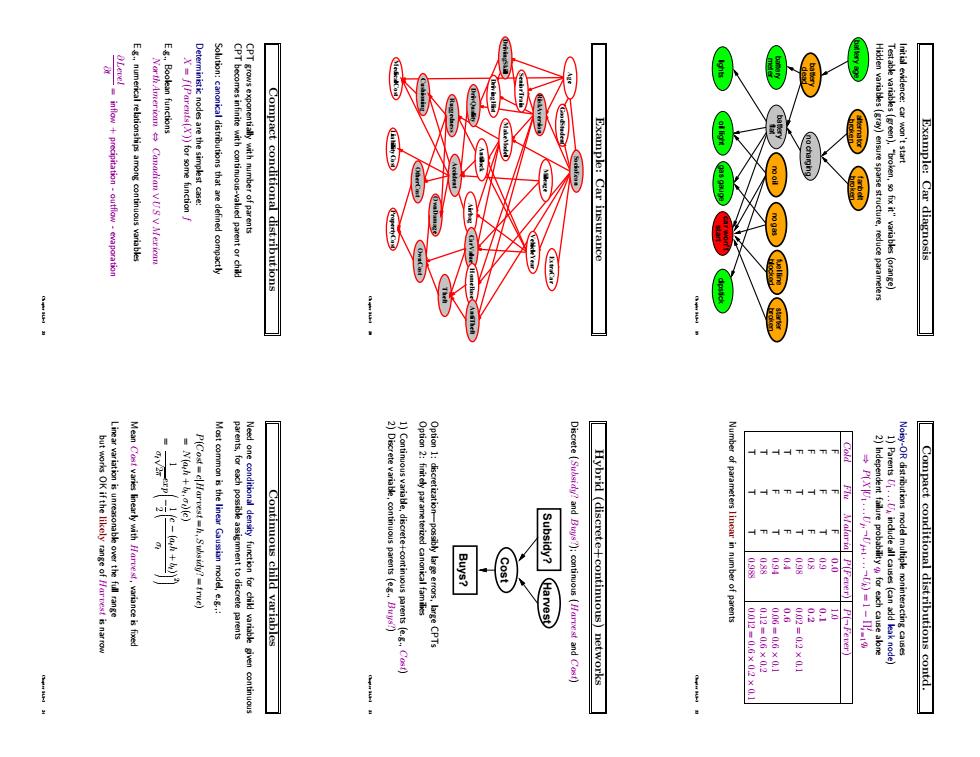
Eumerical relationshipmontinousvariable Compact conditional distributions Example:Car insurance Example:Car diagnosis Continuous child variables Buys? Subsidy?Harvest Discrete [?and Buts?):continuous [Harrest and Cosf) Hybrid (discrete+continuous)networks linear in number of par -02X0 Compact conditional distributions contd
Example: Car diagnosis Initial evidence: car won’t start Testable variables (green), “broken, so fix it” variables (orange) Hidden variables (gray) ensure sparse structure, reduce parameters lights no oil no gas broken starter battery age broken alternator broken fanbelt dead battery no charging flat battery gas gauge blocked fuel line oil light meter battery start car won’t dipstick Chapter 14.1–3 19 Example: Car insurance SocioEcon Age GoodStudent ExtraCar Mileage VehicleYear RiskAversion SeniorTrain DrivingSkill MakeModel DrivingHist DrivQuality Antilock Airbag CarValue HomeBase AntiTheft Theft OwnDamage PropertyCost LiabilityCost MedicalCost Cushioning Ruggedness Accident OtherCost OwnCost Chapter 14.1–3 20 Compact conditional distributions CPT grows exponentially with number of parents CPT becomes infinite with continuous-valued parent or child Solution: canonical distributions that are defined compactly Deterministic nodes are the simplest case: X = f(Parents(X)) for some function f E.g., Boolean functions NorthAmerican ⇔ Canadian ∨ US ∨ Mexican E.g., numerical relationships among continuous variables ∂Level ∂t = inflow + precipitation - outflow - evaporation Chapter 14.1–3 21 Compact conditional distributions contd. Noisy-OR distributions model multiple noninteracting causes 1) Parents U1 . . .Uk include all causes (can add leak node) 2) Independent failure probability qi for each cause alone ⇒ P(X|U1 . . .Uj , ¬Uj+1 . . . ¬Uk) = 1 − Πi j = 1 qi Cold Flu Malaria P(Fever) P(¬Fever) F F F 0.0 1.0 F F T 0.9 0.1 F T F 0.8 0.2 F T T 0.98 0.02 = 0.2 × 0.1 T F F 0.4 0.6 T F T 0.94 0.06 = 0.6 × 0.1 T T F 0.88 0.12 = 0.6 × 0.2 T T T 0.988 0.012 = 0.6 × 0.2 × 0.1 Number of parameters linear in number of parents Chapter 14.1–3 22 Hybrid (discrete+continuous) networks Discrete (Subsidy? and Buys?); continuous (Harvest and Cost) Buys? Harvest Subsidy? Cost Option 1: discretization—possibly large errors, large CPTs Option 2: finitely parameterized canonical families 1) Continuous variable, discrete+continuous parents (e.g., Cost) 2) Discrete variable, continuous parents (e.g., Buys?) Chapter 14.1–3 23 Continuous child variables Need one conditional density function for child variable given continuous parents, for each possible assignment to discrete parents Most common is the linear Gaussian model, e.g.,: P(Cost = c|Harvest = h, Subsidy? = true) = N(ath + bt , σt)(c) = 1 σt √ 2π exp − 2 1 c − (ath + bt) σt 2 Mean Cost varies linearly with Harvest, variance is fixed Linear variation is unreasonable over the full range but works OK if the likely range of Harvest is narrow Chapter 14.1–3 24

圓 1.t'sof the right shape P(Buys?-true Cos whose lcat Why the probit? 1)全T2+33 Continuous child variables > given Cost should be a soft"threshold Discrete variable w/continuous parents Summary shape to probit but much lnger ta Sigmoid (or git)distribution alo used in neural networks: Discrete variable contd
Continuous child variables 0 5 10 0 5 10 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 Cost Harvest P(Cost|Harvest,Subsidy?=true) All-continuous network with LG distributions ⇒ full joint distribution is a multivariate Gaussian Discrete+continuous LG network is a conditional Gaussian network i.e., a multivariate Gaussian over all continuous variables for each combination of discrete variable values Chapter 14.1–3 25 Discrete variable w/ continuous parents Probability of Buys? given Cost should be a “soft” threshold: 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 12 P(Buys?=false|Cost=c) Cost c Probit distribution uses integral of Gaussian: Φ(x) = R −∞ x N(0, 1)(x)dx P(Buys? = true | Cost = c) = Φ((−c + µ)/σ) Chapter 14.1–3 26 Why the probit? 1. It’s sort of the right shape 2. Can view as hard threshold whose location is subject to noise Buys? Cost Cost Noise Chapter 14.1–3 27 Discrete variable contd. Sigmoid (or logit) distribution also used in neural networks: P(Buys? = true | Cost = c) = 1 1 + exp(−2 −c+µ σ ) Sigmoid has similar shape to probit but much longer tails: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 12 P(Buys?=false|Cost=c) Cost c Chapter 14.1–3 28 Summary Bayes nets provide a natural representation for (causally induced) conditional independence Topology + CPTs = compact representation of joint distribution Generally easy for (non)experts to construct Canonical distributions (e.g., noisy-OR) = compact representation of CPTs Continuous variables ⇒ parameterized distributions (e.g., linear Chapter Gaussian) 14.1–3 29