
I 8 anduy 8 HLdVHO OIDOT HH(HO-LSHIH
logic First-order 8 Chapter 1 8 Chapter
TO」u!PJoM sndwnM◇ s3uus4Mung◇ 7O」Jo sonuewas pue xequks◇ 7O为4M◇ ourino
Outline OL? F Why ♦ OL F of semantics and Syntax ♦ sentences with un F ♦ OL F in rld ow umpus W ♦ 2 8 Chapter

g anduy auenbs ypea joy aouaquas auo gullm Kq qdaoxa saenbs quaoelpe ul sazaalq asneo sild,,Kes nouue (enuel lenneu ay!jun) Mod aA!ssaudxa palw!l Kan sey 1o leuo!sodold (nxenuoo uo spuadap Sulueaw aueyM'aBenguel jeunneu ay!jun) quopuadopu!-xoquo s!o Jeuonsodod u!BulueaW jo pue I'g yo 3ulueaw woy panuap s!VI'Ig yo 3ulueaw :Teuoyasodwo s!Jeuonsodold (saseqerep pue saungons erep asow ay!jun) uonewoju!paeau/anunfs!P/jemed sMolleo euosodold se0 puodsauo xeuks Jo saald :Aerelop s!o euosodold ol leuorqsodoId Jo suoo pue sod
logic ositional prop of cons and Pros facts to ond rresp co syntax of pieces : e declarativ is logic ositional Prop rmation info rtial/disjunctive/negated pa ws allo logic ositional Prop databases) and structures data most e (unlik : ositional comp is logic ositional Prop 2, 1 P of and 1, 1 B of meaning from derived is 2, 1 P ∧1, 1 B of meaning t enden text-indep con is logic ositional rop p in Meaning context) on ends dep meaning where language, natural e (unlik er wop ressive exp limited very has logic ositional Prop language) natural e (unlik res” squa adjacent in reezes b cause “pits y sa cannot E.g., re squa each r fo sentence one writing yb except 3 8 Chapter

0 pua'uet4H3ou∂uo'go 3uluu!ply 'pual13 q 'Jo jay4e:suoI4pun时● ·,‘u33M1qs3W0 sumo 'aye p3un0‘o1o)sey0μed3 pisul‘uey1881q0a41oq .·p31μo1s1nw3wud‘sn3oq‘puno1‘p3/:suo4eH● ·sa1 unqua3‘seM‘s3ue8 lleqaseq 'so1o)‘PleuogoW pleuoy‘s3lμoy1‘siaqwnu's3snoy1do9d:s1p3qO● sulenuoo puom ayn sewnsse (a3enguel leuneu ay!)13o]JepJo-is sqoe]sulequoo pjom sawnsse 513o jeuollsodod seajayM 51oI IopIo-SIIH
logic First-order , facts contains rld ow assumes logic ositional rop p Whereas contains rld ow the assumes language) natural e (lik logic rder first-o rs, colo McDonald, Ronald ries, theo ers, numb houses, eople, p : Objects • . . . centuries rs, a w games, baseball ,. . . ried multisto rime, p ogus, b round, red, : Relations • wns, o after, ccurred o r, colo has of, rt pa inside, than, bigger of, rother b . . . een, wet b comes of end than, re mo one of, inning third friend, est b of, father : unctions F • . . . 4 8 Chapter
g8 duo anjen enjaqul uMouy yin jo aagap spe I8o1人zznJ q0338p sipej 人uo3y1KI9eqo1d uMouyun/as]ej/an sau1suo14eIP‘s2p3fq0‘s1ey 51o jejodwaL uMouyun/as]ej/an suo11e1‘s2pafq0‘s1ey 18o1p0-1s1」 umouyun/asjej/an sioej 1o Jeuonsodod quewnlwwo) quawlwwo) 1e318o1oua1s1d与 le1ojouO aen3ue TeJoua8 uI SoIo
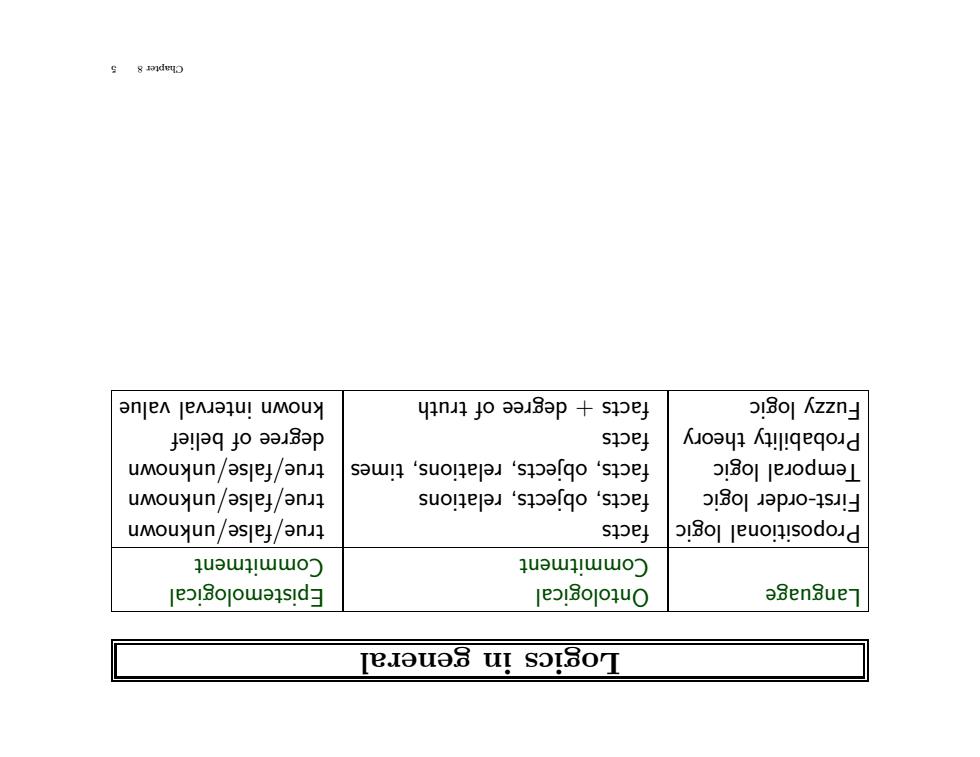
general in Logics Epistemological Ontological Language Commitment Commitment wn true/false/unkno facts logic ositional Prop wn true/false/unkno relations objects, facts, logic rder First-o wn true/false/unkno times relations, objects, facts, logic ral o emp T elief b of degree facts ry theo y Probabilit value interval wn kno truth of degree + facts logic uzzy F 5 8 Chapter

EA siay!uen = Kenb 台←L∧Vs3N1P3uu0) :…q‘D‘f‘x s31qeueΛ ··‘fO63If3T?bS suonoun ……‘<a叫0la saneoipald …‘aOn‘z‘uyor6uy squeisuo) squowal日pIs肥q:IOdJ0XeuS
ts elemen Basic OL: F of tax Syn . . . , BCU, 2 ohn, J ing K Constants . . . >, , other r B Predicates . . . , f O tLeg Lef t, rq S unctions F . . . b, a, , y x, riables aV ⇔ ⇒ ¬ ∨ ∧ Connectives = y Equalit ∃ ∀ Quantifiers 6 8 Chapter

&8md3 (((uyorbuy)fOb Tf T)ubuaT((pDy)fObTf T)ubuaT)< (qDayuoTay Ip.ior uyorbuy)3y01g3 ajqDiion io qungsuoo o (uu.la2‘.·[u.l3)u02pumf=uuBL tw.lag Iw.lag 1o ("w.iagIw.lag)anDopa.id aouaquas owoy seouaquas oiwo!y
tences sen tomic A )n m ter , . . . ,1 m ter ( edicate pr = sentence tomic A 2 m ter =1 m ter r o )n m ter , . . . , 1 m ter ( unction f = erm T e iabl ar v r o constant r o )t heLionhear dT ichar R ohn, J ing K( other r B E.g., ))) ohn J ing K( f O tLeg Lef ( th Leng , )) d ichar R( f O tLeg Lef ( th Leng ( > 7 8 Chapter

88 (亿)<LV(亿T)< (亿)5(亿‘)< (u40rbu2H‘plD4puH)6u1qS←(p.uo叫pH‘u40r6uH)6u1q2S:83 S台SS=ISS∧IS S VIS 'S sannpauuoo guisn saouaquas oiwone woyy apew aue seouequas xejdwo) soouaquas xeldwo
tences sen Complex connectives using sentences atomic from made re a sentences Complex 2 S ⇔1 S , 2 S ⇒1 S , 2 S ∨1 S , 2 S ∧1 S , S¬ ) ohn J ing Kd, ichar R( ing ibl S ⇒) d ichar R ohn, J ing K( ing ibl S E.g. 2) , (1 ≤∨ 2) , (1 > 2) , (1 >¬ ∧ 2) , (1 > 8 8 Chapter

68md0 agpoipa.id Kq o1 pajajal uonejal ay1 ul ale 4u.la1‘.…Tula4Kqo1p1sp3fqo叫4H an s!(ww.ian 'Iw.a)anDopa.d aouaquas olwone uy suonejal jeuonouny sjoqwks uonouny suonejasjoqwks aneoipad spafqo sjoqwks quensuo Joy squaajal sallpads uonenadJaqul wayn Suowe suoneja pue (squawaja ulewop)saoalqo I<suleuoo JepoW uonejadJalul ue pue japow e on adsal yim an ae saouanuas oI IopIo-sIy u yinIL
logic first-order in ruth T retation interp an and del mo a to ect resp with true re a Sentences them among relations and ) elements domain ( objects 1 ≥ contains del Mo r fo referents ecifies sp retation Interp objects → ols symb constant relations → ols symb redicate p relations functional → ols symb function true is )n m ter , . . . ,1 m ter ( edicate pr sentence atomic An n m ter , . . . , 1 m ter yb to referred objects the iff edicate pr yb to referred relation the in re a 9 8 Chapter
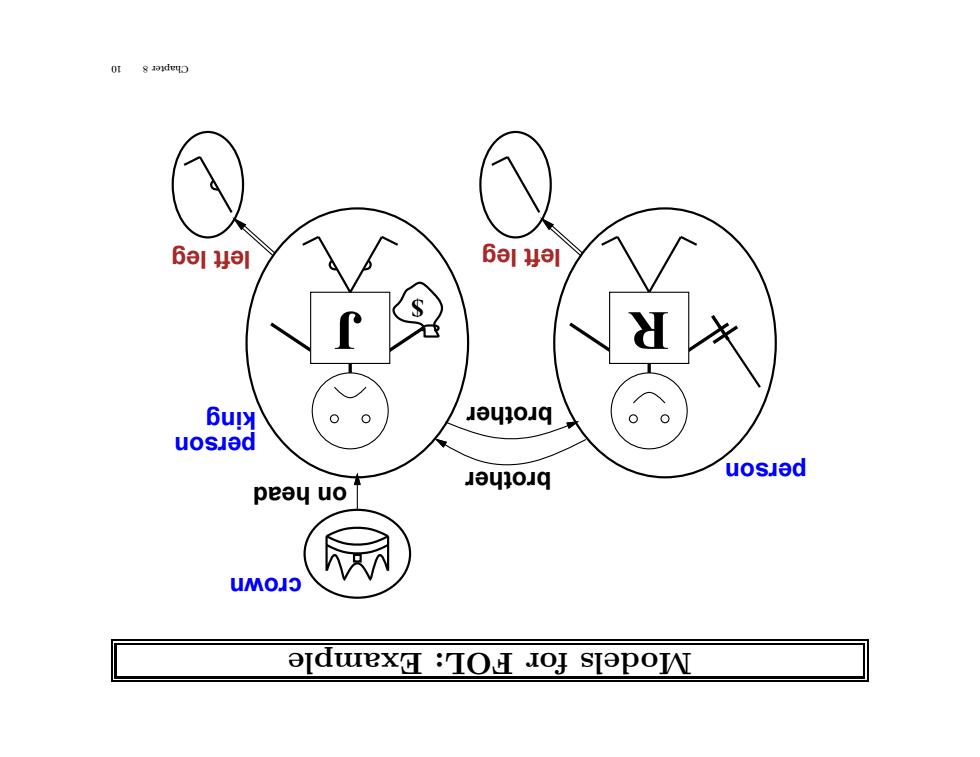
6a11 61 6ulx 0 1410q 00 uosled 叫10q uosJed peay uo UMO1O aldwexH :IOH IoJ SIOpoN
Example OL: F for dels Mo J $ R left leg left leg on head brother brother person person king crown 10 8 Chapter