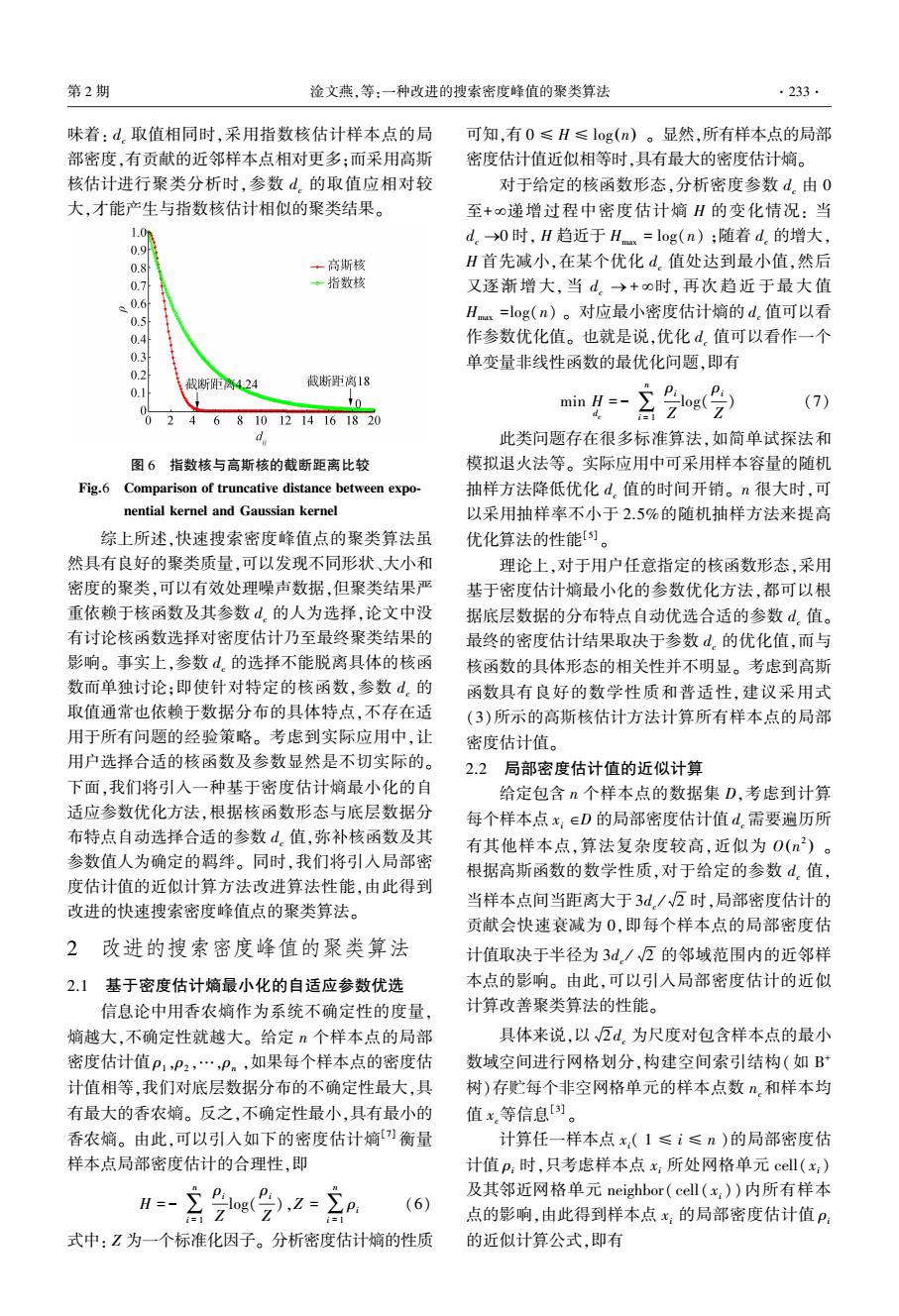
第2期 淦文燕，等：一种改进的搜索密度峰值的聚类算法 .233. 味着：d。取值相同时，采用指数核估计样本点的局 可知，有0≤H≤log(n)。显然，所有样本点的局部 部密度，有贡献的近邻样本点相对更多：而采用高斯 密度估计值近似相等时，具有最大的密度估计嫡。 核估计进行聚类分析时，参数d.的取值应相对较 对于给定的核函数形态，分析密度参数d。由0 大，才能产生与指数核估计相似的聚类结果。 至+0递增过程中密度估计嫡H的变化情况：当 1.0m d。→0时，H趋近于Hx=log(n);随着d.的增大， 0.9 0.8 +高斯核 H首先减小，在某个优化d.值处达到最小值，然后 0.7 ·指数核 又逐渐增大，当d。→+o时，再次趋近于最大值 0.6 0.5 Hx=log(n)。对应最小密度估计嫡的d.值可以看 0.4 作参数优化值。也就是说，优化d。值可以看作一个 0.3 单变量非线性函数的最优化问题，即有 0.2 截断距离4.24 截断距离18 0.1 min H=- (7) 0 2 4 6 8101214161820 d 此类问题存在很多标准算法，如简单试探法和 图6指数核与高斯核的截断距离比较 模拟退火法等。实际应用中可采用样本容量的随机 Fig.6 Comparison of truncative distance between expo- 抽样方法降低优化d。值的时间开销。n很大时，可 nential kernel and Gaussian kernel 以采用抽样率不小于2.5%的随机抽样方法来提高 综上所述，快速搜索密度峰值点的聚类算法虽 优化算法的性能)。 然具有良好的聚类质量，可以发现不同形状、大小和 理论上，对于用户任意指定的核函数形态，采用 密度的聚类，可以有效处理噪声数据，但聚类结果严 基于密度估计嫡最小化的参数优化方法，都可以根 重依赖于核函数及其参数d.的人为选择，论文中没 据底层数据的分布特点自动优选合适的参数d。值。 有讨论核函数选择对密度估计乃至最终聚类结果的 最终的密度估计结果取决于参数d.的优化值，而与 影响。事实上，参数d。的选择不能脱离具体的核函 核函数的具体形态的相关性并不明显。考虑到高斯 数而单独讨论：即使针对特定的核函数，参数d。的 函数具有良好的数学性质和普适性，建议采用式 取值通常也依赖于数据分布的具体特点，不存在适 (3)所示的高斯核估计方法计算所有样本点的局部 用于所有问题的经验策略。考虑到实际应用中，让 密度估计值。 用户选择合适的核函数及参数显然是不切实际的。 2.2局部密度估计值的近似计算 下面，我们将引入一种基于密度估计嫡最小化的自 给定包含n个样本点的数据集D,考虑到计算 适应参数优化方法，根据核函数形态与底层数据分 每个样本点x:∈D的局部密度估计值d.需要遍历所 布特点自动选择合适的参数d值，弥补核函数及其 有其他样本点，算法复杂度较高，近似为0(n2)。 参数值人为确定的羁绊。同时，我们将引入局部密 根据高斯函数的数学性质，对于给定的参数d,值， 度估计值的近似计算方法改进算法性能，由此得到 改进的快速搜索密度峰值点的聚类算法。 当样本点间当距离大于3d./2时，局部密度估计的 贡献会快速衰减为0，即每个样本点的局部密度估 2 改进的搜索密度峰值的聚类算法 计值取决于半径为3d/√万的邻域范围内的近邻样 2.1基于密度估计熵最小化的自适应参数优选 本点的影响。由此，可以引入局部密度估计的近似 信息论中用香农熵作为系统不确定性的度量， 计算改善聚类算法的性能。 熵越大，不确定性就越大。给定n个样本点的局部 具体来说，以√瓦d.为尺度对包含样本点的最小 密度估计值P1,P2,…,P。,如果每个样本点的密度估 数域空间进行网格划分，构建空间索引结构（如B 计值相等，我们对底层数据分布的不确定性最大，具 树)存贮每个非空网格单元的样本点数n,和样本均 有最大的香农嫡。反之，不确定性最小，具有最小的 值x等信息[)。 香农嫡。由此，可以引入如下的密度估计嫡)衡量 计算任一样本点x:(1≤i≤n)的局部密度估 样本点局部密度估计的合理性，即 计值p:时，只考虑样本点x:所处网格单元cell(x:) 及其邻近网格单元neighbor(cell(x:))内所有样本 (6) Z 点的影响，由此得到样本点x:的局部密度估计值P: 式中：Z为一个标准化因子。分析密度估计熵的性质 的近似计算公式，即有味着： ｄｃ 取值相同时，采用指数核估计样本点的局 部密度，有贡献的近邻样本点相对更多；而采用高斯 核估计进行聚类分析时，参数 ｄｃ 的取值应相对较 大，才能产生与指数核估计相似的聚类结果。 图 ６ 指数核与高斯核的截断距离比较 Ｆｉｇ．６ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ｔｒｕｎｃａｔｉｖｅ ｄｉｓｔａｎｃｅ ｂｅｔｗｅｅｎ ｅｘｐｏ⁃ ｎｅｎｔｉａｌ ｋｅｒｎｅｌ ａｎｄ Ｇａｕｓｓｉａｎ ｋｅｒｎｅｌ 综上所述，快速搜索密度峰值点的聚类算法虽 然具有良好的聚类质量，可以发现不同形状、大小和 密度的聚类，可以有效处理噪声数据，但聚类结果严 重依赖于核函数及其参数 ｄｃ 的人为选择，论文中没 有讨论核函数选择对密度估计乃至最终聚类结果的 影响。 事实上，参数 ｄｃ 的选择不能脱离具体的核函 数而单独讨论；即使针对特定的核函数，参数 ｄｃ 的 取值通常也依赖于数据分布的具体特点，不存在适 用于所有问题的经验策略。 考虑到实际应用中，让 用户选择合适的核函数及参数显然是不切实际的。 下面，我们将引入一种基于密度估计熵最小化的自 适应参数优化方法，根据核函数形态与底层数据分 布特点自动选择合适的参数 ｄｃ 值，弥补核函数及其 参数值人为确定的羁绊。 同时，我们将引入局部密 度估计值的近似计算方法改进算法性能，由此得到 改进的快速搜索密度峰值点的聚类算法。 ２ 改进的搜索密度峰值的聚类算法 ２．１ 基于密度估计熵最小化的自适应参数优选 信息论中用香农熵作为系统不确定性的度量， 熵越大，不确定性就越大。 给定 ｎ 个样本点的局部 密度估计值 ρ１ ，ρ２ ，…，ρｎ ，如果每个样本点的密度估 计值相等，我们对底层数据分布的不确定性最大，具 有最大的香农熵。 反之，不确定性最小，具有最小的 香农熵。 由此，可以引入如下的密度估计熵［７］ 衡量 样本点局部密度估计的合理性，即 Ｈ ＝ － ∑ ｎ ｉ ＝ １ ρｉ Ｚ ｌｏｇ（ ρｉ Ｚ ），Ｚ ＝ ∑ ｎ ｉ ＝ １ ρｉ （６） 式中： Ｚ 为一个标准化因子。 分析密度估计熵的性质 可知，有 ０ ≤ Ｈ ≤ ｌｏｇ(ｎ) 。 显然，所有样本点的局部 密度估计值近似相等时，具有最大的密度估计熵。 对于给定的核函数形态，分析密度参数 ｄｃ 由 ０ 至＋ ¥递增过程中密度估计熵 Ｈ 的变化情况： 当 ｄｃ ®０ 时， Ｈ 趋近于 Ｈｍａｘ ＝ ｌｏｇ（ｎ） ；随着 ｄｃ 的增大， Ｈ 首先减小，在某个优化 ｄｃ 值处达到最小值，然后 又逐渐增大， 当 ｄｃ ® ＋ ¥时， 再次趋近于最大值 Ｈｍａｘ ＝ｌｏｇ（ｎ） 。 对应最小密度估计熵的 ｄｃ 值可以看 作参数优化值。 也就是说，优化 ｄｃ 值可以看作一个 单变量非线性函数的最优化问题，即有 ｍｉｎ Ｈ ｄｃ ＝ － ∑ ｎ ｉ ＝ １ ρｉ Ｚ ｌｏｇ（ ρｉ Ｚ ） （７） 此类问题存在很多标准算法，如简单试探法和 模拟退火法等。 实际应用中可采用样本容量的随机 抽样方法降低优化 ｄｃ 值的时间开销。 ｎ 很大时，可 以采用抽样率不小于 ２．５％的随机抽样方法来提高 优化算法的性能［５］ 。 理论上，对于用户任意指定的核函数形态，采用 基于密度估计熵最小化的参数优化方法，都可以根 据底层数据的分布特点自动优选合适的参数 ｄｃ 值。 最终的密度估计结果取决于参数 ｄｃ 的优化值，而与 核函数的具体形态的相关性并不明显。 考虑到高斯 函数具有良好的数学性质和普适性，建议采用式 （３）所示的高斯核估计方法计算所有样本点的局部 密度估计值。 ２．２ 局部密度估计值的近似计算 给定包含 ｎ 个样本点的数据集 Ｄ，考虑到计算 每个样本点 ｘｉ ÎＤ 的局部密度估计值 ｄｃ 需要遍历所 有其他样本点，算法复杂度较高，近似为 Ｏ ｎ ２ ( ) 。 根据高斯函数的数学性质，对于给定的参数 ｄｃ 值， 当样本点间当距离大于 ３ｄｃ ／ ２ 时，局部密度估计的 贡献会快速衰减为 ０，即每个样本点的局部密度估 计值取决于半径为 ３ｄｃ ／ ２ 的邻域范围内的近邻样 本点的影响。 由此，可以引入局部密度估计的近似 计算改善聚类算法的性能。 具体来说，以 ２ ｄｃ 为尺度对包含样本点的最小 数域空间进行网格划分，构建空间索引结构（如 Ｂ + 树）存贮每个非空网格单元的样本点数 ｎｃ和样本均 值 ｘｃ等信息［３］ 。 计算任一样本点 ｘｉ（ １ ≤ ｉ ≤ ｎ ）的局部密度估 计值 ρｉ 时，只考虑样本点 ｘｉ 所处网格单元 ｃｅｌｌ（ ｘｉ） 及其邻近网格单元 ｎｅｉｇｈｂｏｒ（ ｃｅｌｌ（ ｘｉ ）） 内所有样本 点的影响，由此得到样本点 ｘｉ 的局部密度估计值 ρｉ 的近似计算公式，即有 第 ２ 期 淦文燕，等：一种改进的搜索密度峰值的聚类算法 ·２３３·