
第12卷第2期 智能系统学报 Vol.12 No.2 2017年4月 CAAI Transactions on Intelligent Systems Apr.2017 D0I:10.11992/is.201512036 一种改进的搜索密度峰值的聚类算法 淦文燕,刘冲 (解放军理工大学指挥信息系统学院,江苏南京210007) 摘要:聚类是大数据分析与数据挖掘的基础问题。刊登在2014年《Science》杂志上的文章《Clustering by fast search and find of density peaks》提出一种快速搜索密度峰值的聚类算法,算法简单实用,但聚类结果依赖于参数d.的经验 选择。论文提出一种改进的搜索密度峰值的聚类算法,引入密度估计嫡自适应优化算法参数。对比实验结果表明, 改进方法不仅可以较好地解决原算法的参数人为确定的不足,而且具有相对更好的聚类性能。 关键词:数据挖掘:聚类算法:核密度估计:熵 中图分类号:TP311文献标志码:A文章编号:1673-4785(2017)02-0229-07 中文引用格式:淦文燕,刘冲.一种改进的搜索密度峰值的聚类算法[J].智能系统学报,2017,12(2):229-236. 英文引用格式:GAN Wenyan,LIU Chong.An improved clustering algorithm that searches and finds density peaks[J].CAAI transactions on intelligent systems,2017,12(2):229-236. An improved clustering algorithm that searches and finds density peaks GAN Wenyan,LIU Chong College of Command Information System,PLA University of Science and Technology,Nanjing 210007,China) Abstract:Clustering is a fundamental issue for big data analysis and data mining.In July 2014,a paper in the Journal of Science proposed a simple yet effective clustering algorithm based on the idea that cluster centers are characterized by a higher density than their neighbors and having a relatively large distance from points with higher densities.The proposed algorithm can detect clusters of arbitrary shapes and differing densities but is very sensitive to tunable parameter d..In this paper,we propose an improved clustering algorithm that adaptively optimizes pa- rameter de.The time complexity of our algorithm was super-linear with respect to the size of the dataset.Further, our theoretical analysis and experimental results show the effectiveness and efficiency of our improved algorithm. Keywords:data mining;clustering algorithms;kernel density estimation;entropy 互联网时代,随着社交网络、电子商务与移动通 似性尽量大)。与分类不同,聚类无须明确的类标 信等技术的蓬勃发展,人类社会进入以PB级数据 记,无须区分训练集与测试集,是一种寻求数据自然 信息为特征的大数据时代。如何从海量复杂数据集 聚簇结构的非监督学习方法,可以产生问题中数据 中自动发现新知识、新规律,实现从数据到知识到决 的概括性描述,可以自动构建分类层次结构,具有更 策的挑战与跨越1-】,成为各行各业普遍面临的严 好的普适性:同时,聚类又具有不确定性。对于给定 峻技术挑战。 的数据集,聚类结果不仅依赖于实际的数据分布,而 所谓聚类,就是根据描述事物的某些属性,将 且取决于问题的应用背景与目标,不存在唯一正确 事物聚集成若干类,使得类间相似性尽量小,类内相 的聚类划分。正由于这种普适性与不确定性,使聚 类问题比分类问题更复杂、更具挑战性,被认为是大 收稿日期:2015-12-31. 基金项目:国家自然科学基金项目(60974086). 数据分析与数据挖掘的基础问题,也成为统计、模式 通信作者:刘冲.E-mail:c1368542460@126.com. 识别、机器学习、人工智能等诸多学科领域中一个非
第 12 卷第 2 期 智 能 系 统 学 报 Vol.12 №.2 2017 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2017 DOI:10.11992 / tis.201512036 一种改进的搜索密度峰值的聚类算法 淦文燕,刘冲 (解放军理工大学 指挥信息系统学院,江苏 南京 210007) 摘 要:聚类是大数据分析与数据挖掘的基础问题。 刊登在 2014 年《Science》杂志上的文章《Clustering by fast search and find of density peaks》提出一种快速搜索密度峰值的聚类算法,算法简单实用,但聚类结果依赖于参数 dc 的经验 选择。 论文提出一种改进的搜索密度峰值的聚类算法,引入密度估计熵自适应优化算法参数。 对比实验结果表明, 改进方法不仅可以较好地解决原算法的参数人为确定的不足,而且具有相对更好的聚类性能。 关键词:数据挖掘;聚类算法;核密度估计;熵 中图分类号: TP311 文献标志码:A 文章编号:1673-4785(2017)02-0229-07 中文引用格式:淦文燕,刘冲. 一种改进的搜索密度峰值的聚类算法[J]. 智能系统学报, 2017, 12(2): 229-236. 英文引用格式: GAN Wenyan, LIU Chong. An improved clustering algorithm that searches and finds density peaks[ J]. CAAI transactions on intelligent systems, 2017, 12(2): 229-236. An improved clustering algorithm that searches and finds density peaks GAN Wenyan, LIU Chong (College of Command Information System, PLA University of Science and Technology, Nanjing 210007, China) Abstract:Clustering is a fundamental issue for big data analysis and data mining. In July 2014, a paper in the Journal of Science proposed a simple yet effective clustering algorithm based on the idea that cluster centers are characterized by a higher density than their neighbors and having a relatively large distance from points with higher densities. The proposed algorithm can detect clusters of arbitrary shapes and differing densities but is very sensitive to tunable parameter dc . In this paper, we propose an improved clustering algorithm that adaptively optimizes pa⁃ rameter dc. The time complexity of our algorithm was super⁃linear with respect to the size of the dataset. Further, our theoretical analysis and experimental results show the effectiveness and efficiency of our improved algorithm. Keywords: data mining; clustering algorithms; kernel density estimation; entropy 收稿日期:2015-12-31. 基金项目:国家自然科学基金项目(60974086). 通信作者:刘冲. E⁃mail:lc1368542460@ 126.com. 互联网时代,随着社交网络、电子商务与移动通 信等技术的蓬勃发展,人类社会进入以 PB 级数据 信息为特征的大数据时代。 如何从海量复杂数据集 中自动发现新知识、新规律,实现从数据到知识到决 策的挑战与跨越[1-2] ,成为各行各业普遍面临的严 峻技术挑战。 所谓聚类,就是根据描述事物的某些属性, 将 事物聚集成若干类,使得类间相似性尽量小,类内相 似性尽量大[3] 。 与分类不同,聚类无须明确的类标 记,无须区分训练集与测试集,是一种寻求数据自然 聚簇结构的非监督学习方法,可以产生问题中数据 的概括性描述,可以自动构建分类层次结构,具有更 好的普适性;同时,聚类又具有不确定性。 对于给定 的数据集,聚类结果不仅依赖于实际的数据分布,而 且取决于问题的应用背景与目标,不存在唯一正确 的聚类划分。 正由于这种普适性与不确定性,使聚 类问题比分类问题更复杂、更具挑战性,被认为是大 数据分析与数据挖掘的基础问题,也成为统计、模式 识别、机器学习、人工智能等诸多学科领域中一个非

.230 智能系统学报 第12卷 常活跃且非常重要的研究热点[3-) 3)指数核估计 2014年《Science》杂志上刊登了一篇题为 p,= (4) 《Clustering by fast search and find of density peaks》)t的 ∑e() 论文口,论文提出一种快速搜索和发现密度峰值的 式中:d为样本点x:、x间的距离,采用满足三角不 聚类算法。算法将具有局部极大密度估计值的样本 等式的距离度量,如欧氏距离:d>0是预先指定的 点视为聚类中心,通过快速搜索聚类中心,将每一个 密度估计参数,相当于核函数的窗宽。 非中心样本点沿着密度递增的最近邻方向迭代划分 高密度最近邻距离6则定义为x到具有更大密 给相应的聚类中心,实现数据划分。算法思路新颖, 度估计值的最近邻样本点的距离,即 简单实用,具有良好的聚类质量,能够发现任意形 6=min (d) (5) jpi>PI 状、大小和密度的聚类,能够有效处理噪声和离群数 显然,具有全局最大密度估计值的样本点不存 据,对人脸等高维非结构化数据具有良好的适用性。 在高密度最近邻,可简单地令其高密度最近邻距离 虽然论文的局限性遭到众多读者的质疑,如聚类结 等于所有样本点间距离的最大值。 果严重依赖于密度参数d,的仔细选择,但整体上可 1.2基于决策图的聚类划分 以为聚类算法设计提供一种新思路。 通过计算每个样本点x,(1≤i≤n)的局部密度 本文深入探讨了快速搜索密度峰值点的聚类算 估计值d。和高密度最近邻距离6,算法将原始数据 法[)的局限性,引入基于密度估计嫡最小化的自适 集D映射到由局部密度估计p和高密度最近邻距离 应参数优化方法弥补其核函数及其参数值人为确定 6组成的二维特征空间中。直觉上,代表聚类中心的 的羁绊,提出一种改进的搜索密度峰值点的聚类算 样本点应同时具有较大的局部密度估计值p和较大 法。在重现论文算法并获得与原作者相同实验结果 的高密度最近邻距离P。由此,通过特征空间中决策 的基础上,用改进算法重新聚类。对比实验结果表 图的可视化,可以实现基于中心的聚类划分。 明,改进算法不仅能有效解决原算法的参数优选问 图1所示为论文实验采用的模拟测试数据集及 题,而且具有相对更好的聚类性能。 其聚类结果)。测试数据包含4000个样本点,分 别取自6个不同的二维正态分布,还有一些噪声数 1快速搜索密度峰值的聚类算法 据。图1(a)所示为采用式(2)所示的截断核估计 给定数据集D={x1,x2,…,x},快速搜索 且参数d.取最小2%的距离做截断时(即d.取值为 密度峰值点的聚类算法)。假设聚类中心对应 所有样本点间距离的最小2%的距离中的最大距 某些具有局部极大密度估计值的样本点,这些样 离),测试数据集投影到以局部密度估计P值为横 本点可以看作由低密度样本点所包围的“高密度 轴、以高密度最近邻距离δ为纵轴的二维空间中形 峰值点”,距离其他高密度近邻样本相对较远。 成的决策图):显然,图中虚线框选出的5个样本 算法通过快速搜索和发现代表聚类中心的“高密 点同时具有较大的局部密度估计值ρ和高密度最近 度峰值点”,将每个非中心样本点沿着密度估计 邻距离P,可以被选为5个聚类中心,相应聚类结果 值递增的最近邻方向迭代移动到相应的聚类中 如图1(b)所示。4000个样本点被划分为5个类和 心,实现数据划分。这里涉及两个基本概念:局 噪声数据,每个类用与中心样本点相同的数字来标 部密度估计和高密度最近邻距离。 记。其中,第五类最大,包含多于1500个样本点, 1.1局部密度估计与高密度最近邻距离 第一类最小,仅有200多个样本点。显然,算法具有 x:∈D,1≤i≤n,局部密度估计值d.定义为 良好的聚类质量,可以发现不同形状、大小和密度的 p,=∑x(dg,d) (1) 聚类,可以有效处理噪声数据。 1对i 但算法中存在一个重要参数,即密度参数d。。 式中:X(·)相当于核密度估计的核函数,论文给出 论文认为,参数d,的取值虽然会影响样本点的局部 3种可选的核函数形态,相应的密度估计公式如下: 密度估计与高密度最近邻距离,但不会严重影响最 1)截断核估计 终的聚类结果,通常选取所有样本点间距离的最小 p=a,-d),X)=,<0 (0,x≥0(2) 1%~2%做截断即可(即令d。取值为所有样本点间 距离的最小1%~2%的距离中的最大距离)。但重 2)高斯核估计 现论文算法及其实验结果时,我们发现,核函数的选 。£倒: (3) 择及其参数d的取值都会严重影响最终聚类结果
常活跃且非常重要的研究热点[3-5] 。 2014 年 《 Science 》 杂 志 上 刊 登 了 一 篇 题 为 《Clustering by fast search and find of density peaks》的 论文[1] ,论文提出一种快速搜索和发现密度峰值的 聚类算法。 算法将具有局部极大密度估计值的样本 点视为聚类中心,通过快速搜索聚类中心,将每一个 非中心样本点沿着密度递增的最近邻方向迭代划分 给相应的聚类中心,实现数据划分。 算法思路新颖, 简单实用,具有良好的聚类质量,能够发现任意形 状、大小和密度的聚类,能够有效处理噪声和离群数 据,对人脸等高维非结构化数据具有良好的适用性。 虽然论文的局限性遭到众多读者的质疑,如聚类结 果严重依赖于密度参数 dc 的仔细选择,但整体上可 以为聚类算法设计提供一种新思路。 本文深入探讨了快速搜索密度峰值点的聚类算 法[1]的局限性,引入基于密度估计熵最小化的自适 应参数优化方法弥补其核函数及其参数值人为确定 的羁绊,提出一种改进的搜索密度峰值点的聚类算 法。 在重现论文算法并获得与原作者相同实验结果 的基础上,用改进算法重新聚类。 对比实验结果表 明,改进算法不仅能有效解决原算法的参数优选问 题,而且具有相对更好的聚类性能。 1 快速搜索密度峰值的聚类算法 给定数据集 D = x1 ,x2 ,…,xn { } ,快速搜索 密度峰值点的聚类算法[ 1] 。 假设聚类中心对应 某些具有局部极大密度估计值的样本点,这些样 本点可以看作由低密度样本点所包围的“ 高密度 峰值点” ,距离其他高密度近邻样本相对较远。 算法通过快速搜索和发现代表聚类中心的“ 高密 度峰值点” ,将每个非中心样本点沿着密度估计 值递增的最近邻方向迭代移动到相应的聚类中 心,实现数据划分。 这里涉及两个基本概念:局 部密度估计和高密度最近邻距离。 1.1 局部密度估计与高密度最近邻距离 ∀xi ∈ D , 1 ≤ i ≤ n ,局部密度估计值 dc 定义为 ρi = 1≤∑ j≠i≤n χ dij,dc ( ) (1) 式中: χ (·) 相当于核密度估计的核函数,论文给出 3 种可选的核函数形态,相应的密度估计公式如下: 1)截断核估计 ρi = ∑ j≠i χ dij - dc ( ) , χ (x) = 1, x < 0 0, x ≥ 0 { (2) 2)高斯核估计 ρi = ∑ j≠i e - d ij d c ( ) 2 (3) 3)指数核估计 ρi = ∑ j≠i e - d ij d 2 c ( ) (4) 式中:dij为样本点 xi、xj间的距离,采用满足三角不 等式的距离度量,如欧氏距离;dc >0 是预先指定的 密度估计参数,相当于核函数的窗宽。 高密度最近邻距离 δi 则定义为 xi到具有更大密 度估计值的最近邻样本点的距离,即 δi = min j:ρj > ρi dij ( ) (5) 显然,具有全局最大密度估计值的样本点不存 在高密度最近邻,可简单地令其高密度最近邻距离 等于所有样本点间距离的最大值。 1.2 基于决策图的聚类划分 通过计算每个样本点 xi( 1 ≤i ≤n )的局部密度 估计值 dc 和高密度最近邻距离 δi,算法将原始数据 集 D 映射到由局部密度估计 ρ 和高密度最近邻距离 δ 组成的二维特征空间中。 直觉上,代表聚类中心的 样本点应同时具有较大的局部密度估计值 ρ 和较大 的高密度最近邻距离 ρ。 由此,通过特征空间中决策 图的可视化,可以实现基于中心的聚类划分。 图 1 所示为论文实验采用的模拟测试数据集及 其聚类结果[1] 。 测试数据包含 4 000 个样本点,分 别取自 6 个不同的二维正态分布,还有一些噪声数 据。 图 1(a) 所示为采用式(2) 所示的截断核估计 且参数 dc 取最小 2%的距离做截断时(即 dc 取值为 所有样本点间距离的最小 2% 的距离中的最大距 离),测试数据集投影到以局部密度估计 ρ 值为横 轴、以高密度最近邻距离 δ 为纵轴的二维空间中形 成的决策图[1] ;显然,图中虚线框选出的 5 个样本 点同时具有较大的局部密度估计值 ρ 和高密度最近 邻距离 ρ,可以被选为 5 个聚类中心,相应聚类结果 如图 1(b)所示。 4 000 个样本点被划分为 5 个类和 噪声数据,每个类用与中心样本点相同的数字来标 记。 其中,第五类最大,包含多于 1 500 个样本点, 第一类最小,仅有 200 多个样本点。 显然,算法具有 良好的聚类质量,可以发现不同形状、大小和密度的 聚类,可以有效处理噪声数据。 但算法中存在一个重要参数,即密度参数 dc 。 论文认为,参数 dc 的取值虽然会影响样本点的局部 密度估计与高密度最近邻距离,但不会严重影响最 终的聚类结果,通常选取所有样本点间距离的最小 1% ~2%做截断即可(即令 dc 取值为所有样本点间 距离的最小 1% ~ 2%的距离中的最大距离)。 但重 现论文算法及其实验结果时,我们发现,核函数的选 择及其参数 dc 的取值都会严重影响最终聚类结果。 ·230· 智 能 系 统 学 报 第 12 卷
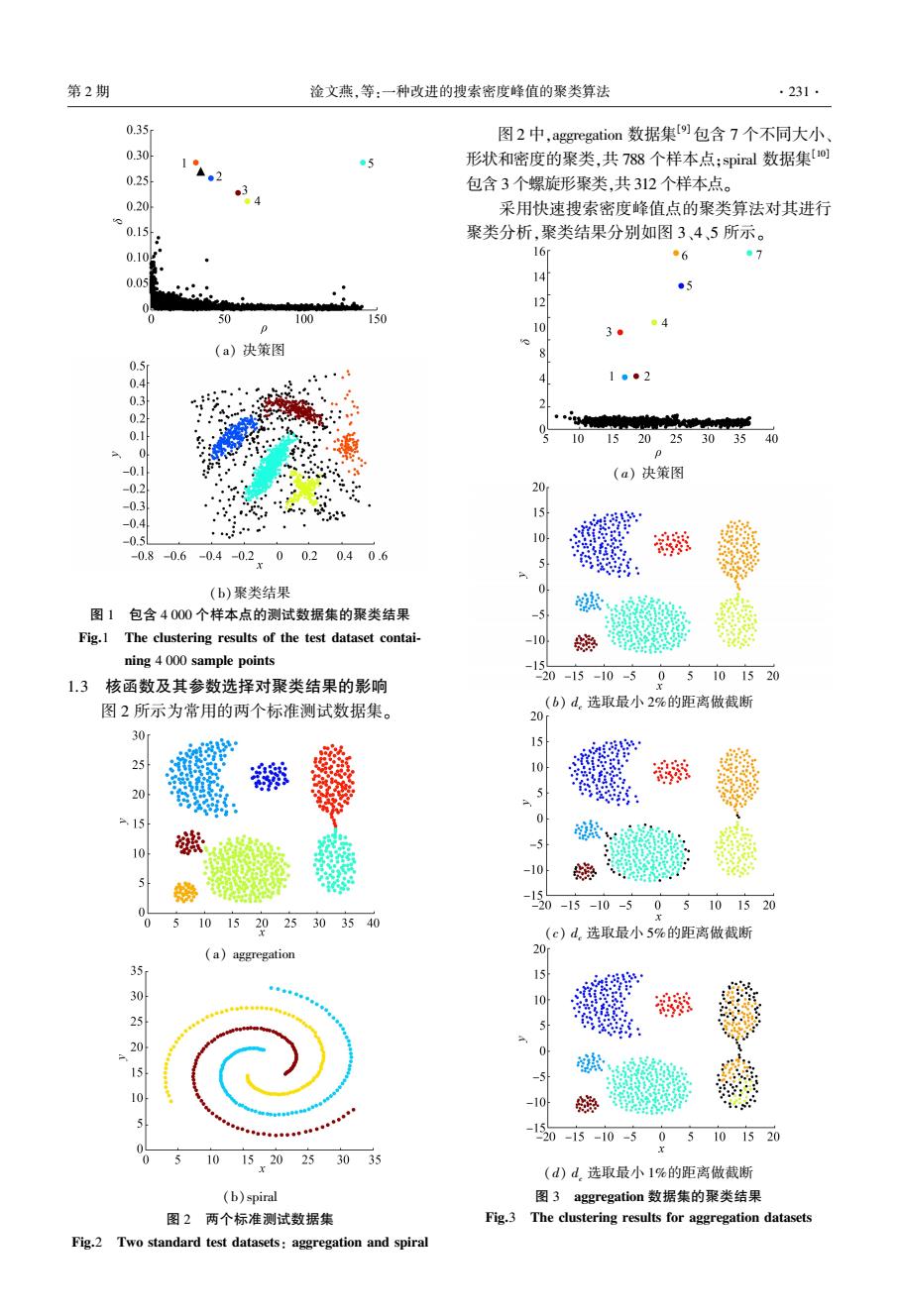
第2期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 ·231 0.35 图2中,aggregation数据集9包含7个不同大小 0.30 12 05 形状和密度的聚类,共788个样本点:spiral数据集o 0.25 包含3个螺旋形聚类,共312个样本点。 0.20 采用快速搜索密度峰值点的聚类算法对其进行 0.15 聚类分析,聚类结果分别如图3、4、5所示。 0.10g 16 ●6 7 0.05 14 ●5 0 50 100 150 ●4 3 (a)决策图 0.5 0.4 1●2 2 0.2 10152025303540 0 p -0. (a)决策图 -0.2 ” 20 -0.3 -04 0. 0.8-0.6-04-02x0020406 (b)聚类结果 图1包含4000个样本点的测试数据集的聚类结果 Fig.1 The clustering results of the test dataset contai- -10 嫩 ning 4 000 sample points -15 1.3 核函数及其参数选择对聚类结果的影响 20-15-10-505101520 图2所示为常用的两个标准测试数据集。 b)d选取最小2%的距离做截断 20 30 29 10 5 1 0 5 10 -10 5 15 -20-15-10-505101520 510152025303540 (c)d.选取最小5%的距离做截断 (a)aggregation 20 35 302520 15 10 -10 120-15-10-5 05101520 1015.20253035 (d)d选取最小1%的距离做截断 (b)spiral 图3 aggregation数据集的聚类结果 图2两个标准测试数据集 Fig.3 The clustering results for aggregation datasets Fig.2 Two standard test datasets:aggregation and spiral
(a) 决策图 (b)聚类结果 图 1 包含 4 000 个样本点的测试数据集的聚类结果 Fig.1 The clustering results of the test dataset contai⁃ ning 4 000 sample points 1.3 核函数及其参数选择对聚类结果的影响 图 2 所示为常用的两个标准测试数据集。 (a) aggregation (b)spiral 图 2 两个标准测试数据集 Fig.2 Two standard test datasets: aggregation and spiral 图 2 中,aggregation 数据集[9]包含 7 个不同大小、 形状和密度的聚类,共 788 个样本点;spiral 数据集[10] 包含 3 个螺旋形聚类,共 312 个样本点。 采用快速搜索密度峰值点的聚类算法对其进行 聚类分析,聚类结果分别如图 3、4、5 所示。 (a) 决策图 (b) dc 选取最小 2%的距离做截断 (c) dc 选取最小 5%的距离做截断 (d) dc 选取最小 1%的距离做截断 图 3 aggregation 数据集的聚类结果 Fig.3 The clustering results for aggregation datasets 第 2 期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 ·231·

.232 智能系统学报 第12卷 7 2.3 图3(a)、3(b)所示为采用式(4)的指数核估计 6 且参数d。取最小2%的距离做截断时,aggregation数 1。 据集得到的聚类决策图及相应聚类结果。由图3 (b)可知,聚类算法可以正确识别aggregation数据 集的7个不同大小、形状和密度的聚类。但如果采 用截断核,且令d.分别取最小5%或1%的距离做截 断,聚类结果如图3(c)、3(d)所示。图3(c)中,聚 类质量明显下降,很多样本点被误分噪声数据。由 10 15 20 25 此可见,聚类结果对参数d.的取值非常敏感,进一 (a)决策图 步分析核函数选择对聚类结果的影响。定性讨论核 函数及其参数d.的选择对聚类结果的影响。给定 20 包含n个样本点的数据集D,根据式(1),任一样本 15 点x,∈D处的局部密度估计值d.等价于以其他样本 点x∈D为中心的、n-1个核函数的叠加,其中j≠ i。这表示每个样本点的局部密度估计值等于所有 其他样本点在该处的“贡献”的叠加,“贡献”的大小 依赖于两点间的距离。 10 图4(a)、4(b)所示为采用指数核估计且d.选 -155-10 -5 0x5101520 取最小2%的距离做截断时,spiral数据集得到聚类 决策图及其聚类结果,显然聚类结果可以正确识别 (b)d选取最小3%的距离做截断 spiral数据集的3个螺旋形聚类。但如果采用式 图4 spiral数据集的聚类结果(采用指数核估计) (5)所示的高斯核估计,令d。分别选取最小1%或 Fig.4 The clustering results for aggregation datasets using exponential kernel estimation) 2%的距离做截断时,聚类结果如图5(a)、5(b)所 20 示。显然,当d。取值固定时,聚类结果对核函数的 选择也非常敏感。事实上,采用高斯核估计对spiral 数据集进行聚类分析,d。要选取大于2%的距离做 截断,才能得到相对较好的聚类结果。而不是简单 地令d。选取所有样本点间距离的最小1%-2%做截 断即可。 -10 采用式(2)所示的截断核估计时,每个样本点 5-10 x:处的密度估计值d为离散值,等价于x,的d邻域 -5 05101520 内近邻样本点的个数,密度估计具有局域性。这里 (a)d。选取最小1%的距离做截断 的密度参数d。表示截断距离,当样本点间距离超过 20 d.时,其贡献可以忽略不计:而采用式(3)所示的高 斯核估计时,每个样本点x,处的局部密度估计值d 10 为连续值,参数d,的作用也是控制密度估计的局域 性,但近邻样本点的贡献会随距离的增长而衰减。 根据高斯函数的数学性质,当距离大于3d。/2时, 样本点的贡献会快速衰减为0,指示着高斯核估计 -10 的截断距离近似为3d。/2;类似地,采用式(4)所 -15-10-50.5101520 示的指数核估计时,每个样本点x:处的局部密度估 计值d.虽然也是连续值,但相对于高斯核估计,近 (b)d选取最小2%的距离做截断 邻样本点对x:处密度估计的贡献随距离增长而衰 图5 spiral数据集的聚类结果(采用高斯核估计) Fig.5 The clustering results for aggregation datasets 减的速度相对较慢,指示着相对更大的截断距离。 (using gaussian kernel estimation)】 图6所示为d。=2时指数核与高斯核的截断距 离比较,图中指数核的截断距离远大于高斯核,这意
(a) 决策图 (b) dc 选取最小 3%的距离做截断 图 4 spiral 数据集的聚类结果(采用指数核估计) Fig. 4 The clustering results for aggregation datasets (using exponential kernel estimation) (a) dc 选取最小 1%的距离做截断 (b) dc 选取最小 2%的距离做截断 图 5 spiral 数据集的聚类结果(采用高斯核估计) Fig. 5 The clustering results for aggregation datasets (using gaussian kernel estimation) 图 3(a)、3(b)所示为采用式(4)的指数核估计 且参数 dc 取最小 2%的距离做截断时,aggregation 数 据集得到的聚类决策图及相应聚类结果。 由图 3 (b)可知,聚类算法可以正确识别 aggregation 数据 集的 7 个不同大小、形状和密度的聚类。 但如果采 用截断核,且令 dc 分别取最小 5%或 1%的距离做截 断,聚类结果如图 3(c)、3(d)所示。 图 3( c)中,聚 类质量明显下降,很多样本点被误分噪声数据。 由 此可见,聚类结果对参数 dc 的取值非常敏感,进一 步分析核函数选择对聚类结果的影响。 定性讨论核 函数及其参数 dc 的选择对聚类结果的影响。 给定 包含 n 个样本点的数据集 D,根据式(1),任一样本 点 xi ÎD 处的局部密度估计值 dc 等价于以其他样本 点 xjÎD 为中心的、n-1 个核函数的叠加,其中 j ≠ i 。 这表示每个样本点的局部密度估计值等于所有 其他样本点在该处的“贡献”的叠加,“贡献”的大小 依赖于两点间的距离。 图 4(a)、4( b)所示为采用指数核估计且 dc 选 取最小 2%的距离做截断时,spiral 数据集得到聚类 决策图及其聚类结果,显然聚类结果可以正确识别 spiral 数据集的 3 个螺旋形聚类。 但如果采用式 (5)所示的高斯核估计,令 dc 分别选取最小 1%或 2%的距离做截断时,聚类结果如图 5( a)、5( b) 所 示。 显然,当 dc 取值固定时,聚类结果对核函数的 选择也非常敏感。 事实上,采用高斯核估计对 spiral 数据集进行聚类分析, dc 要选取大于 2%的距离做 截断,才能得到相对较好的聚类结果。 而不是简单 地令 dc 选取所有样本点间距离的最小 1%-2%做截 断即可。 采用式(2)所示的截断核估计时,每个样本点 xi 处的密度估计值 dc 为离散值,等价于 xi 的 dc 邻域 内近邻样本点的个数,密度估计具有局域性。 这里 的密度参数 dc 表示截断距离,当样本点间距离超过 dc 时,其贡献可以忽略不计;而采用式(3)所示的高 斯核估计时,每个样本点 xi 处的局部密度估计值 dc 为连续值,参数 dc 的作用也是控制密度估计的局域 性,但近邻样本点的贡献会随距离的增长而衰减。 根据高斯函数的数学性质,当距离大于 3dc / 2 时, 样本点的贡献会快速衰减为 0,指示着高斯核估计 的截断距离近似为 3dc / 2 ;类似地,采用式(4) 所 示的指数核估计时,每个样本点 xi 处的局部密度估 计值 dc 虽然也是连续值,但相对于高斯核估计,近 邻样本点对 xi 处密度估计的贡献随距离增长而衰 减的速度相对较慢,指示着相对更大的截断距离。 图 6 所示为 dc = 2 时指数核与高斯核的截断距 离比较,图中指数核的截断距离远大于高斯核,这意 ·232· 智 能 系 统 学 报 第 12 卷
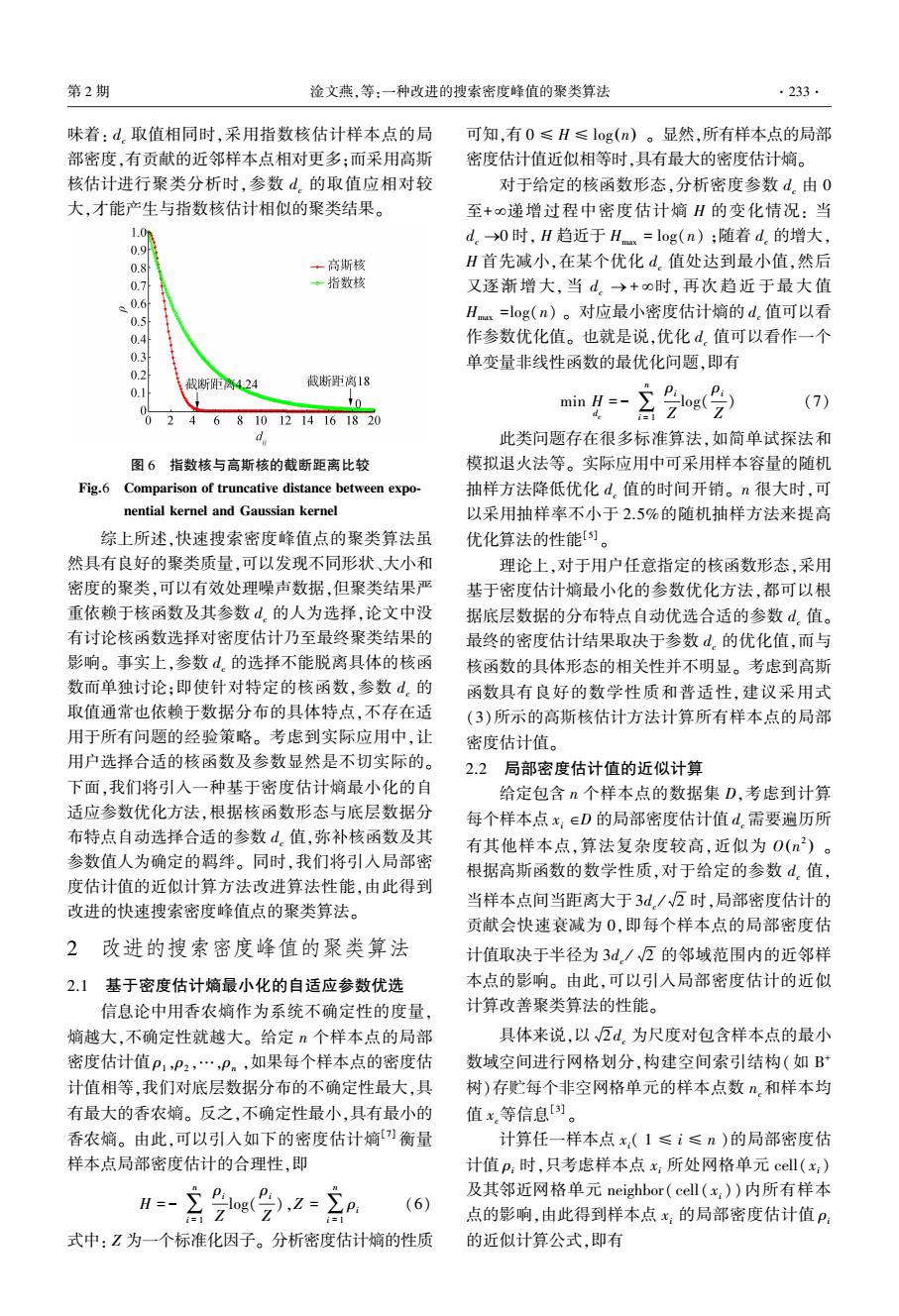
第2期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 .233. 味着:d。取值相同时,采用指数核估计样本点的局 可知,有0≤H≤log(n)。显然,所有样本点的局部 部密度,有贡献的近邻样本点相对更多:而采用高斯 密度估计值近似相等时,具有最大的密度估计嫡。 核估计进行聚类分析时,参数d.的取值应相对较 对于给定的核函数形态,分析密度参数d。由0 大,才能产生与指数核估计相似的聚类结果。 至+0递增过程中密度估计嫡H的变化情况:当 1.0m d。→0时,H趋近于Hx=log(n);随着d.的增大, 0.9 0.8 +高斯核 H首先减小,在某个优化d.值处达到最小值,然后 0.7 ·指数核 又逐渐增大,当d。→+o时,再次趋近于最大值 0.6 0.5 Hx=log(n)。对应最小密度估计嫡的d.值可以看 0.4 作参数优化值。也就是说,优化d。值可以看作一个 0.3 单变量非线性函数的最优化问题,即有 0.2 截断距离4.24 截断距离18 0.1 min H=- (7) 0 2 4 6 8101214161820 d 此类问题存在很多标准算法,如简单试探法和 图6指数核与高斯核的截断距离比较 模拟退火法等。实际应用中可采用样本容量的随机 Fig.6 Comparison of truncative distance between expo- 抽样方法降低优化d。值的时间开销。n很大时,可 nential kernel and Gaussian kernel 以采用抽样率不小于2.5%的随机抽样方法来提高 综上所述,快速搜索密度峰值点的聚类算法虽 优化算法的性能)。 然具有良好的聚类质量,可以发现不同形状、大小和 理论上,对于用户任意指定的核函数形态,采用 密度的聚类,可以有效处理噪声数据,但聚类结果严 基于密度估计嫡最小化的参数优化方法,都可以根 重依赖于核函数及其参数d.的人为选择,论文中没 据底层数据的分布特点自动优选合适的参数d。值。 有讨论核函数选择对密度估计乃至最终聚类结果的 最终的密度估计结果取决于参数d.的优化值,而与 影响。事实上,参数d。的选择不能脱离具体的核函 核函数的具体形态的相关性并不明显。考虑到高斯 数而单独讨论:即使针对特定的核函数,参数d。的 函数具有良好的数学性质和普适性,建议采用式 取值通常也依赖于数据分布的具体特点,不存在适 (3)所示的高斯核估计方法计算所有样本点的局部 用于所有问题的经验策略。考虑到实际应用中,让 密度估计值。 用户选择合适的核函数及参数显然是不切实际的。 2.2局部密度估计值的近似计算 下面,我们将引入一种基于密度估计嫡最小化的自 给定包含n个样本点的数据集D,考虑到计算 适应参数优化方法,根据核函数形态与底层数据分 每个样本点x:∈D的局部密度估计值d.需要遍历所 布特点自动选择合适的参数d值,弥补核函数及其 有其他样本点,算法复杂度较高,近似为0(n2)。 参数值人为确定的羁绊。同时,我们将引入局部密 根据高斯函数的数学性质,对于给定的参数d,值, 度估计值的近似计算方法改进算法性能,由此得到 改进的快速搜索密度峰值点的聚类算法。 当样本点间当距离大于3d./2时,局部密度估计的 贡献会快速衰减为0,即每个样本点的局部密度估 2 改进的搜索密度峰值的聚类算法 计值取决于半径为3d/√万的邻域范围内的近邻样 2.1基于密度估计熵最小化的自适应参数优选 本点的影响。由此,可以引入局部密度估计的近似 信息论中用香农熵作为系统不确定性的度量, 计算改善聚类算法的性能。 熵越大,不确定性就越大。给定n个样本点的局部 具体来说,以√瓦d.为尺度对包含样本点的最小 密度估计值P1,P2,…,P。,如果每个样本点的密度估 数域空间进行网格划分,构建空间索引结构(如B 计值相等,我们对底层数据分布的不确定性最大,具 树)存贮每个非空网格单元的样本点数n,和样本均 有最大的香农嫡。反之,不确定性最小,具有最小的 值x等信息[)。 香农嫡。由此,可以引入如下的密度估计嫡)衡量 计算任一样本点x:(1≤i≤n)的局部密度估 样本点局部密度估计的合理性,即 计值p:时,只考虑样本点x:所处网格单元cell(x:) 及其邻近网格单元neighbor(cell(x:))内所有样本 (6) Z 点的影响,由此得到样本点x:的局部密度估计值P: 式中:Z为一个标准化因子。分析密度估计熵的性质 的近似计算公式,即有
味着: dc 取值相同时,采用指数核估计样本点的局 部密度,有贡献的近邻样本点相对更多;而采用高斯 核估计进行聚类分析时,参数 dc 的取值应相对较 大,才能产生与指数核估计相似的聚类结果。 图 6 指数核与高斯核的截断距离比较 Fig.6 Comparison of truncative distance between expo⁃ nential kernel and Gaussian kernel 综上所述,快速搜索密度峰值点的聚类算法虽 然具有良好的聚类质量,可以发现不同形状、大小和 密度的聚类,可以有效处理噪声数据,但聚类结果严 重依赖于核函数及其参数 dc 的人为选择,论文中没 有讨论核函数选择对密度估计乃至最终聚类结果的 影响。 事实上,参数 dc 的选择不能脱离具体的核函 数而单独讨论;即使针对特定的核函数,参数 dc 的 取值通常也依赖于数据分布的具体特点,不存在适 用于所有问题的经验策略。 考虑到实际应用中,让 用户选择合适的核函数及参数显然是不切实际的。 下面,我们将引入一种基于密度估计熵最小化的自 适应参数优化方法,根据核函数形态与底层数据分 布特点自动选择合适的参数 dc 值,弥补核函数及其 参数值人为确定的羁绊。 同时,我们将引入局部密 度估计值的近似计算方法改进算法性能,由此得到 改进的快速搜索密度峰值点的聚类算法。 2 改进的搜索密度峰值的聚类算法 2.1 基于密度估计熵最小化的自适应参数优选 信息论中用香农熵作为系统不确定性的度量, 熵越大,不确定性就越大。 给定 n 个样本点的局部 密度估计值 ρ1 ,ρ2 ,…,ρn ,如果每个样本点的密度估 计值相等,我们对底层数据分布的不确定性最大,具 有最大的香农熵。 反之,不确定性最小,具有最小的 香农熵。 由此,可以引入如下的密度估计熵[7] 衡量 样本点局部密度估计的合理性,即 H = - ∑ n i = 1 ρi Z log( ρi Z ),Z = ∑ n i = 1 ρi (6) 式中: Z 为一个标准化因子。 分析密度估计熵的性质 可知,有 0 ≤ H ≤ log(n) 。 显然,所有样本点的局部 密度估计值近似相等时,具有最大的密度估计熵。 对于给定的核函数形态,分析密度参数 dc 由 0 至+ ¥递增过程中密度估计熵 H 的变化情况: 当 dc ®0 时, H 趋近于 Hmax = log(n) ;随着 dc 的增大, H 首先减小,在某个优化 dc 值处达到最小值,然后 又逐渐增大, 当 dc ® + ¥时, 再次趋近于最大值 Hmax =log(n) 。 对应最小密度估计熵的 dc 值可以看 作参数优化值。 也就是说,优化 dc 值可以看作一个 单变量非线性函数的最优化问题,即有 min H dc = - ∑ n i = 1 ρi Z log( ρi Z ) (7) 此类问题存在很多标准算法,如简单试探法和 模拟退火法等。 实际应用中可采用样本容量的随机 抽样方法降低优化 dc 值的时间开销。 n 很大时,可 以采用抽样率不小于 2.5%的随机抽样方法来提高 优化算法的性能[5] 。 理论上,对于用户任意指定的核函数形态,采用 基于密度估计熵最小化的参数优化方法,都可以根 据底层数据的分布特点自动优选合适的参数 dc 值。 最终的密度估计结果取决于参数 dc 的优化值,而与 核函数的具体形态的相关性并不明显。 考虑到高斯 函数具有良好的数学性质和普适性,建议采用式 (3)所示的高斯核估计方法计算所有样本点的局部 密度估计值。 2.2 局部密度估计值的近似计算 给定包含 n 个样本点的数据集 D,考虑到计算 每个样本点 xi ÎD 的局部密度估计值 dc 需要遍历所 有其他样本点,算法复杂度较高,近似为 O n 2 ( ) 。 根据高斯函数的数学性质,对于给定的参数 dc 值, 当样本点间当距离大于 3dc / 2 时,局部密度估计的 贡献会快速衰减为 0,即每个样本点的局部密度估 计值取决于半径为 3dc / 2 的邻域范围内的近邻样 本点的影响。 由此,可以引入局部密度估计的近似 计算改善聚类算法的性能。 具体来说,以 2 dc 为尺度对包含样本点的最小 数域空间进行网格划分,构建空间索引结构(如 B + 树)存贮每个非空网格单元的样本点数 nc和样本均 值 xc等信息[3] 。 计算任一样本点 xi( 1 ≤ i ≤ n )的局部密度估 计值 ρi 时,只考虑样本点 xi 所处网格单元 cell( xi) 及其邻近网格单元 neighbor( cell( xi )) 内所有样本 点的影响,由此得到样本点 xi 的局部密度估计值 ρi 的近似计算公式,即有 第 2 期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 ·233·

.234. 智能系统学报 第12卷 P:≈ ∑,e(自)产+Phc)(8) 000个样本点。图7(a)所示为原算法[]的聚类结 e cell(E)y≠i 果,其参数d.值是一个经验值0.03,即选取最小2% eigoe.(x;)= 的距离做截断:图7(b)所示为改进算法的聚类结 Ce neighbor(cell() 果,其参数d.值是通过密度估计嫡最小化得到的优 (9) 化值,略大于论文)实验采用的经验值,但聚类质 其中P恤.(x,)的计算公式代表邻近网格 量相对更好,而且抗噪声能力更好。 单元内的样本点对P:的贡献。此时计算任一样本 0.5 点的局部密度估计值所需时间开销仅为空间索引时 间,即O(log(na),nd<n为非空网格单元数, 而构造空间索引结构所需时间为O(og(n)),算 法总的时间复杂度近似为O(log(nd))。具体算法 描述如下: 2.3改进算法描述 给定数据集D={x1,x2,…,x},改进的快速搜 0.5 索密度峰值的聚类算法可以描述如下。 -0.8-0.6-0.4-0.200.20.40.6 算法改进的搜索密度峰值的聚类算法 (a)原算法(d.=0.03) (ICADEP) 0.5 输入数据集D={x1,x2,…,xn},抽样个数 nsample 输出数据划分Π。 算法步骤: I)随机抽取nap。个样本点组成抽样数据集 SampleSet; 2)d.=Optimal_Parameter(SampleSet);/用抽 样数据集优化估计密度参数d。; -08060402.002040.6 3)Map CreateMap(D,- );/以 为尺度 (b)ICADEP算法(d.=0.05) 图74000个随机样本点的聚类结果比较 对空间进行网格划分并构建索引树: Fig.7 Comparison of clustering results of 4000 random 4)p =Density_Estimation(D,Map,d);// sample points 算所有样本点的局部密度估计值P1,P2,…,Pn; 图8(a)所示为原算法聚类结果,参数d.选取 5)8=NN_Distance(D,Map,p);/按照局部 最小2%的距离做截断,即d.=2.23:而图8(b)所示 密度估从大到小的顺序,计算所有样本点的高密度 的改进算法聚类结果中,通过密度估计嫡最小化得 最所邻距离81,…,6n; 到的优化d。值虽然略小于论文实验的经验值,即 6)C=Decision_Graph(D,p,δ)://形成决策 d.=2.02,但聚类结果同样能够正确识别原始数据分 图,根据用户交互,确定代表聚类中心的样本子集: 布的7个内在的数据类。 7)Π=Partition(D,C);/将所有非中心样本 20 15 点沿着密度估计值递增的最近邻方向,迭代划分给 10 相应的聚类中心,实现数据划分。 - 3实验结果与比较 -5 这里采用图1、2所示的测试数据集检验改进算 法ICADEP的有效性。所有程序用软件Matlab2011 102势 -15 实现,测试在一台PC机(i5-3210MCPU、8GHz内 20-15-10-5 05101520 存、Win7)上进行,聚类结果如图7~9所示。图7所 (a)原算法(d。=2.23) 示的测试数据包含6个聚类和一些噪声数据,共4
ρi ≈ ∑ xj∈cell xi ( ) ∧j≠i e - d ij d c ( ) 2 + φneighbor_cells xi ( ) (8) φneighbor_cells(xi) = C∈neigh∑bor(cell(xi )) nc·e - d x i ,x c ( ) d c ( ) 2 (9) 其中 φneighbor_cells xi ( ) 的计算公式代表邻近网格 单元内的样本点对 ρi 的贡献。 此时计算任一样本 点的局部密度估计值所需时间开销仅为空间索引时 间,即 O( log( ngrid )),ngrid <<n 为非空网格单元数, 而构造空间索引结构所需时间为 O( log( ngrid )),算 法总的时间复杂度近似为 O(log(ngrid ))。 具体算法 描述如下: 2.3 改进算法描述 给定数据集 D = x1 ,x2 ,…,xn { } ,改进的快速搜 索密度峰值的聚类算法可以描述如下。 算法 改 进 的 搜 索 密 度 峰 值 的 聚 类 算 法 (ICADEP) 输入 数据集 D = x1 ,x2 ,…,xn { } ,抽样个数 nsample ; 输出 数据划分P。 算法步骤: 1)随机抽取 nsample 个样本点组成抽样数据集 SampleSet; 2) dc = Optimal_Parameter (SampleSet); / / 用抽 样数据集优化估计密度参数 dc ; 3)Map = CreateMap(D, dc 2 ); / / 以 dc 2 为尺度 对空间进行网格划分并构建索引树; 4) ρ = Density_Estimation(D, Map, dc ); / / 计 算所有样本点的局部密度估计值 ρ1 ,ρ2 ,…,ρn ; 5) δ = NN_Distance(D, Map, ρ ); / / 按照局部 密度估从大到小的顺序,计算所有样本点的高密度 最所邻距离 δ1 ,…,δn ; 6)C = Decision_Graph(D, ρ, δ ); / / 形成决策 图,根据用户交互,确定代表聚类中心的样本子集; 7)P= Partition (D, C); / / 将所有非中心样本 点沿着密度估计值递增的最近邻方向,迭代划分给 相应的聚类中心,实现数据划分。 3 实验结果与比较 这里采用图 1、2 所示的测试数据集检验改进算 法 ICADEP 的有效性。 所有程序用软件 Matlab2011 实现,测试在一台 PC 机( i5-3210M CPU、8GHz 内 存、Win7)上进行,聚类结果如图 7~9 所示。 图 7 所 示的测试数据包含 6 个聚类和一些噪声数据,共 4 000 个样本点。 图 7( a) 所示为原算法[1] 的聚类结 果,其参数 dc 值是一个经验值 0.03,即选取最小 2% 的距离做截断;图 7( b) 所示为改进算法的聚类结 果,其参数 dc 值是通过密度估计熵最小化得到的优 化值,略大于论文[1] 实验采用的经验值,但聚类质 量相对更好,而且抗噪声能力更好。 (a)原算法[1] ( dc = 0.03 ) (b)ICADEP 算法( dc = 0.05 ) 图 7 4 000 个随机样本点的聚类结果比较 Fig.7 Comparison of clustering results of 4 000 random sample points 图 8(a)所示为原算法聚类结果,参数 dc 选取 最小 2%的距离做截断,即 dc = 2.23;而图 8(b)所示 的改进算法聚类结果中,通过密度估计熵最小化得 到的优化 dc 值虽然略小于论文[1]实验的经验值,即 dc = 2.02,但聚类结果同样能够正确识别原始数据分 布的 7 个内在的数据类。 (a)原算法[1] ( dc = 2.23 ) ·234· 智 能 系 统 学 报 第 12 卷
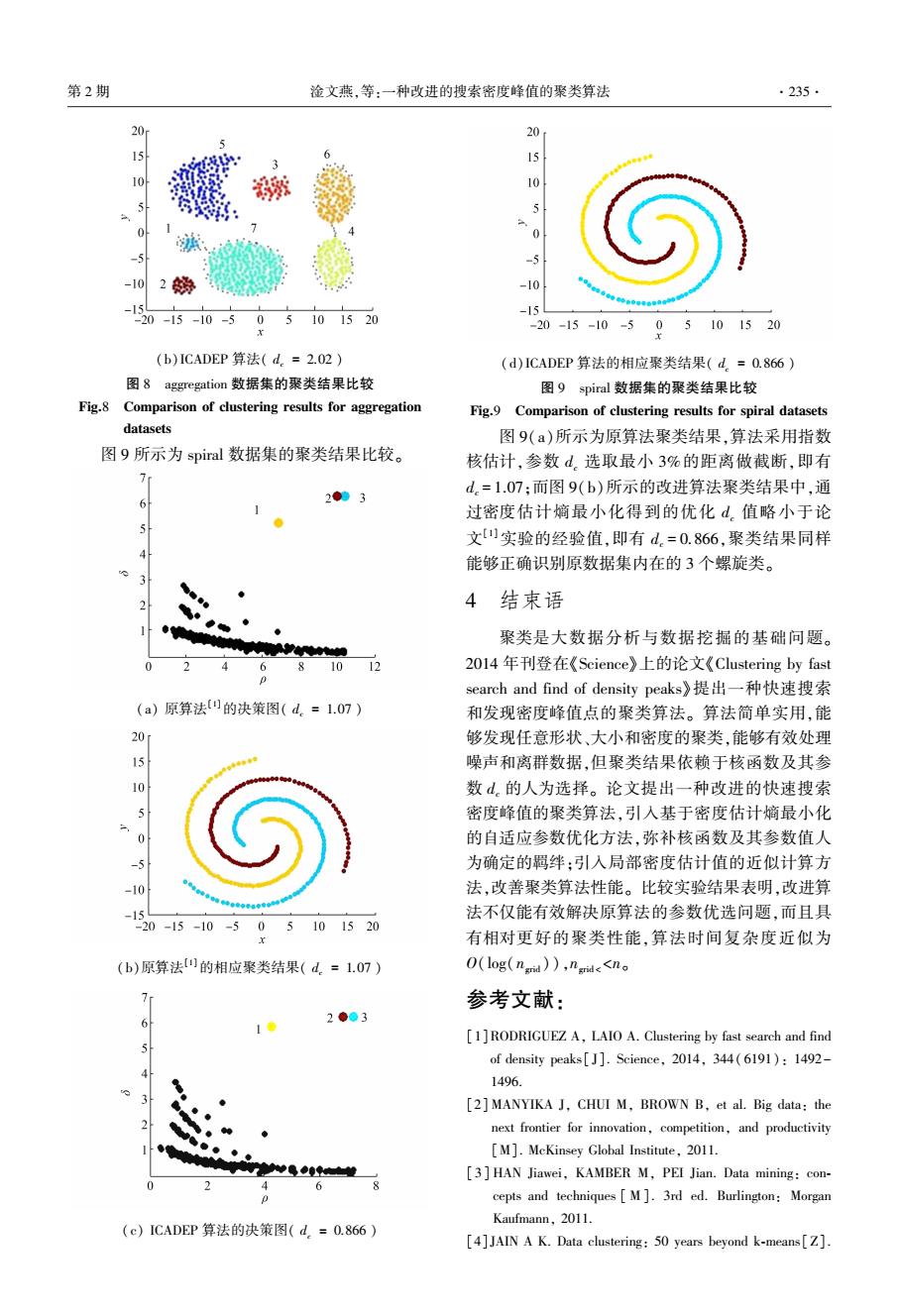
第2期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 .235. 20 20 15 15 10 0 -5 2妫 -10 -1 -15 20-15-10-505101520 -20-15-10-505101520 (b)ICADEP算法(d.=2.02) (d)ICADEP算法的相应聚类结果(d=O.866) 图8 aggregation数据集的聚类结果比较 图9 spiral数据集的聚类结果比较 Fig.8 Comparison of clustering results for aggregation Fig.9 Comparison of clustering results for spiral datasets datasets 图9(a)所示为原算法聚类结果,算法采用指数 图9所示为spiral数据集的聚类结果比较。 核估计,参数d.选取最小3%的距离做截断,即有 d.=1.07:而图9(b)所示的改进算法聚类结果中,通 2●3 过密度估计嫡最小化得到的优化d值略小于论 5 文实验的经验值,即有d.=0.866,聚类结果同样 能够正确识别原数据集内在的3个螺旋类。 4结束语 聚类是大数据分析与数据挖掘的基础问题。 6 81012 20l4年f刊登在《Science》上的论文《Clustering by fast 0 search and find of density peaks》提出一种快速搜索 (a)原算法0的决策图(d.=1.07) 和发现密度峰值点的聚类算法。算法简单实用,能 20 够发现任意形状、大小和密度的聚类,能够有效处理 噪声和离群数据,但聚类结果依赖于核函数及其参 10 数d。的人为选择。论文提出一种改进的快速搜索 密度峰值的聚类算法,引入基于密度估计熵最小化 的自适应参数优化方法,弥补核函数及其参数值人 为确定的羁绊:引入局部密度估计值的近似计算方 -10 法,改善聚类算法性能。比较实验结果表明,改进算 -15 法不仅能有效解决原算法的参数优选问题,而且具 20-15-10-505101520 有相对更好的聚类性能,算法时间复杂度近似为 (b)原算法山的相应聚类结果(d.=1.07) O(log(nad)),nid<<no 参考文献: 6 2●●3 [1]RODRIGUEZ A,LAIO A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492- 1496. [2]MANYIKA J,CHUI M,BROWN B,et al.Big data:the next frontier for innovation,competition,and productivity [M].McKinsey Global Institute,2011. [3]HAN Jiawei,KAMBER M,PEI Jian.Data mining:con- 6 cepts and techniques M].3rd ed.Burlington:Morgan Kaufmann,2011. (c)ICADEP算法的决策图(d,=O.866) [4]JAIN A K.Data clustering:50 years beyond k-means[Z]
(b)ICADEP 算法( dc = 2.02 ) 图 8 aggregation 数据集的聚类结果比较 Fig.8 Comparison of clustering results for aggregation datasets 图 9 所示为 spiral 数据集的聚类结果比较。 (a) 原算法[1]的决策图( dc = 1.07 ) (b)原算法[1]的相应聚类结果( dc = 1.07 ) (c) ICADEP 算法的决策图( dc = 0.866 ) (d)ICADEP 算法的相应聚类结果( dc = 0.866 ) 图 9 spiral 数据集的聚类结果比较 Fig.9 Comparison of clustering results for spiral datasets 图 9(a)所示为原算法聚类结果,算法采用指数 核估计,参数 dc 选取最小 3%的距离做截断,即有 dc = 1.07;而图 9(b)所示的改进算法聚类结果中,通 过密度估计熵最小化得到的优化 dc 值略小于论 文[1]实验的经验值,即有 dc = 0.866,聚类结果同样 能够正确识别原数据集内在的 3 个螺旋类。 4 结束语 聚类是大数据分析与数据挖掘的基础问题。 2014 年刊登在《Science》上的论文《Clustering by fast search and find of density peaks》提出一种快速搜索 和发现密度峰值点的聚类算法。 算法简单实用,能 够发现任意形状、大小和密度的聚类,能够有效处理 噪声和离群数据,但聚类结果依赖于核函数及其参 数 dc 的人为选择。 论文提出一种改进的快速搜索 密度峰值的聚类算法,引入基于密度估计熵最小化 的自适应参数优化方法,弥补核函数及其参数值人 为确定的羁绊;引入局部密度估计值的近似计算方 法,改善聚类算法性能。 比较实验结果表明,改进算 法不仅能有效解决原算法的参数优选问题,而且具 有相对更好的聚类性能,算法时间复杂度近似为 O(log(ngrid )),ngrid < <n。 参考文献: [1]RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[ J]. Science, 2014, 344( 6191): 1492- 1496. [2] MANYIKA J, CHUI M, BROWN B, et al. Big data: the next frontier for innovation, competition, and productivity [M]. McKinsey Global Institute, 2011. [ 3] HAN Jiawei, KAMBER M, PEI Jian. Data mining: con⁃ cepts and techniques [ M]. 3rd ed. Burlington: Morgan Kaufmann, 2011. [4]JAIN A K. Data clustering: 50 years beyond k⁃means[Z]. 第 2 期 淦文燕,等:一种改进的搜索密度峰值的聚类算法 ·235·

·236 智能系统学报 第12卷 Pattern Recognition Letters,2009. [9]GIONIS A,MANNILA H,TSAPARAS P.Clustering aggre- [5]唐杰,东昱晓,蒋朦,等.SIGKDD二十周年庆典[J].中 gation[J].ACM transactions on knowledge discovery from 国计算机学会通讯,2014,10(10):58-64. data,2007,1(1):Article No.4. [6]http://comments.sicencemag.org/content/10.1126/science. 作者简介: 1242072[0L/EB]. 淦文燕,女,副教授。主要研究方 [7]淦文燕,李德毅.基于核密度估计的层次聚类算法[J]· 向为人工智能,数据挖掘,机器学习。 系统仿真学报,2004,16(2):302-305. GAN Wenyan,LI Deyi.Hierarchical clustering based on kernel density estimation[J].Journal of System Simulation, 2004,16(2):302-305. [8]ESTER M,KRIEGEL H,SANDER J,et al.A density 刘冲,男,硕士研究生,主要研究方 based algorithm for discovering clusters in large spatial data- 向为大数据分析,数据挖掘。 bases with noise[C]//Proceedings of the 2nd international conference on knowledge discovery and data mining.Port- land.1996:226-231. 2017第二届群体智能和进化计算会议 2017 2nd Conference on Swarm Intelligence and Evolutionary Computation CSIEC) Optimization is at the heart of many real world problems in various fields ranging from scientific research to industry and commerce.To tackle complex real world problems,experts have been looking into natural processes and creatures for years.Over the last years,nature-inspired search techniques and optimization algorithms have been became the subject of many researches and currently are used in various field of science,ranging from scientific research to industry and com- merce.The two main families of algorithms that primarily constitute this field today are the evolutionary computing methods and the swarm intelligence algorithms.Many heuristic algorithms in each group are invented where each one has its own distinguishing features.Furthermore,encountering various problems,algorithms are enhanced by offering different strate- gies including inventing different variants,producing specialized operators,co-evolution,hybridization,dynamic control- ling,and so on.2nd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC2017)is an opportunity for researchers to share their contemporary knowledge in the field of nature-inspired intelligent computation based on the prin- ciples of swarm and evolutionary algorithms.The conference welcomes significant contributions in both English and Farsi languages. Topics of interest include but are not limited to: Search Domains Problem Domains Application Domains Website:http://csiec2017en.uk.ac.ir/App_Web/%28Guest%29/Default.aspx
Pattern Recognition Letters, 2009. [5]唐杰, 东昱晓, 蒋朦, 等. SIGKDD 二十周年庆典[J]. 中 国计算机学会通讯, 2014, 10(10): 58-64. [6]http: / / comments.sicencemag.org / content / 10.1126 / science. 1242072[OL/ EB]. [7]淦文燕, 李德毅. 基于核密度估计的层次聚类算法[ J]. 系统仿真学报, 2004, 16(2): 302-305. GAN Wenyan, LI Deyi. Hierarchical clustering based on kernel density estimation[J]. Journal of System Simulation, 2004, 16(2): 302-305. [8] ESTER M, KRIEGEL H, SANDER J, et al. A density based algorithm for discovering clusters in large spatial data⁃ bases with noise[C] / / Proceedings of the 2nd international conference on knowledge discovery and data mining. Port⁃ land, 1996: 226-231. [9]GIONIS A, MANNILA H, TSAPARAS P. Clustering aggre⁃ gation[ J]. ACM transactions on knowledge discovery from data, 2007, 1(1): Article No.4. 作者简介: 淦文燕,女,副教授。 主要研究方 向为人工智能,数据挖掘,机器学习。 刘冲,男,硕士研究生,主要研究方 向为大数据分析,数据挖掘。 2017 第二届群体智能和进化计算会议 2017 2nd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC) Optimization is at the heart of many real world problems in various fields ranging from scientific research to industry and commerce. To tackle complex real world problems, experts have been looking into natural processes and creatures for years. Over the last years, nature⁃inspired search techniques and optimization algorithms have been became the subject of many researches and currently are used in various field of science, ranging from scientific research to industry and com⁃ merce. The two main families of algorithms that primarily constitute this field today are the evolutionary computing methods and the swarm intelligence algorithms. Many heuristic algorithms in each group are invented where each one has its own distinguishing features. Furthermore, encountering various problems, algorithms are enhanced by offering different strate⁃ gies including inventing different variants, producing specialized operators, co⁃evolution, hybridization, dynamic control⁃ ling, and so on. 2nd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC2017) is an opportunity for researchers to share their contemporary knowledge in the field of nature⁃inspired intelligent computation based on the prin⁃ ciples of swarm and evolutionary algorithms. The conference welcomes significant contributions in both English and Farsi languages. Topics of interest include but are not limited to: Search Domains Problem Domains Application Domains Website:http: / / csiec2017en.uk.ac.ir/ App_Web / %28Guest%29 / Default.aspx ·236· 智 能 系 统 学 报 第 12 卷