
第11卷第1期 智能系统学报 Vol.11 No.1 2016年2月 CAAI Transactions on Intelligent Systems Feh.2016 D0I:10.11992/is.201506022 网络出版地址:htp://www.cmki.net/kcms/detail/23.1538.TP.20151229.0837.010.html 运用核聚类和偏最小二乘回归的歌唱声音转换 方鹏12,3,李贤13,汪增福12,3 (1.中国科学技术大学信息科学技术学院,安徽合肥230027:2.中国科学院合肥智能机械研究所,安徽合肥 230031:3.语音及语言信息处理国家工程实验室,安徽合肥230027) 摘要:语音转换是计算机听觉领域的热点问题之一,将歌声运用于语音转换是一种新的研究方向,同时拓宽了语 音转换的应用范围。经典的高斯混合模型的方法在少量训练数据时会出现过拟合的现象,而且在转换时并未有效 利用音乐信息。为此提出一种歌唱声音转换方法以实现少量训练数据时的音色转换,并且利用歌曲的基频信息提 高转换歌声的声音质量。该方法使用核聚类和偏最小二乘回归进行训练得到转换函数,采用梅尔对数频谱近似 (MLSA)滤波器对源歌唱声音的波形直接进行滤波来获得转换后的歌唱声音,以此提高转换歌声的声音质量。实验 结果表明,在少量训练数据时,该方法在相似度和音质方面都有更好的效果,说明在少量训练数据时该方法优于传 统的高斯混合模型的方法。 关键词:计算机视觉:语音转换;歌唱声音:核聚类:偏最小二乘回归:高斯混合模型:MLSA 中图分类号:TN912:TP37文献标志码:A文章编号:1673-4785(2016)01-0055-06 中文引用格式:方鹏,李贤,汪增福.运用核聚类和偏最小二乘回归的歌唱声音转换[J].智能系统学报,2016,11(1):55-60. 英文引用格式:FANG Peng,LI Xian,WANG Zengfu..Conversion of singing voice based on kernel clustering and partial least squares regression[J].CAAI Transactions on Intelligent Systems,2016,11(1):55-60. Conversion of singing voice based on kernel clustering and partial least squares regression FANG Peng'2.3,LI Xian'3,WANG Zengfu'.2.3 (1.Department of Automation,University of Science and Technology of China,Hefei 230027,China;2.Institute of Intelligent Ma- chines,Chinese Academy of Sciences,Hefei 230031,China;3.National Engineering Laboratory of Speech and Language Information Processing,Hefei 230027,China) Abstract:Voice conversion is a popular topic in the field of computer hearing,and the application of singing voices to voice conversion is a relatively new research direction,which widens the application scope of voice conversion. When a training dataset is small,the conventional Gaussian mixture model (GMM)method may cause overfitting and insufficient utilization of music information.In this study,we propose a method for converting the voice timbre of a source singer into that of a target singer and employ fundamental frequency to improve the converted singing voice quality.We use kernel clustering and partial least squares regression to train the dataset,thereby obtaining the conversion function.To improve the converted singing voice quality,we applied the Mel log spectrum approxi- mation (MLSA)filter,which synthesizes the converted singing voice by filtering the source singing waveform. Based on our experiment results,the proposed method demonstrates better voice similarity and quality,and there- fore is a better choice than the GMM-based method when the training dataset is small. Keywords:computer vision;voice conversion;singing voice;kernel clustering;partial least squares regression; Gaussian mixture model;Mel log spectrum approximation 语音转换是一项非常热门的技术,在近20年间 不改变语义信息的情况下,使其声音听起来像是另 开始涌现,它可以通过修饰一个源说话者的声音,在 一个特定的人所说的。由于每个人生理特征的限 制,使得我们在发音的时候不能自由的转换音色,只 收稿日期:2015-06-11.网络出版日期:2015-12-29. 基金项目:国家自然科学基金资助项目(61472393,613031350). 能在某种程度上轻微地改变自己的音色,但是当说 通信作者:汪增福.E-mail:zfwang(@ustc.cdu.cm
第 11 卷第 1 期 智 能 系 统 学 报 Vol.11 №.1 2016 年 2 月 CAAI Transactions on Intelligent Systems Feb. 2016 DOI:10.11992 / tis.201506022 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20151229.0837.010.html 运用核聚类和偏最小二乘回归的歌唱声音转换 方鹏1,2,3 ,李贤1,3 ,汪增福1,2,3 (1.中国科学技术大学 信息科学技术学院,安徽 合肥 230027; 2.中国科学院 合肥智能机械研究所,安徽 合肥 230031; 3.语音及语言信息处理国家工程实验室,安徽 合肥 230027) 摘 要:语音转换是计算机听觉领域的热点问题之一,将歌声运用于语音转换是一种新的研究方向,同时拓宽了语 音转换的应用范围。 经典的高斯混合模型的方法在少量训练数据时会出现过拟合的现象,而且在转换时并未有效 利用音乐信息。 为此提出一种歌唱声音转换方法以实现少量训练数据时的音色转换,并且利用歌曲的基频信息提 高转换歌声的声音质量。 该方法使用核聚类和偏最小二乘回归进行训练得到转换函数,采用梅尔对数频谱近似 (MLSA)滤波器对源歌唱声音的波形直接进行滤波来获得转换后的歌唱声音,以此提高转换歌声的声音质量。 实验 结果表明,在少量训练数据时,该方法在相似度和音质方面都有更好的效果,说明在少量训练数据时该方法优于传 统的高斯混合模型的方法。 关键词:计算机视觉;语音转换;歌唱声音;核聚类;偏最小二乘回归;高斯混合模型;MLSA 中图分类号:TN912;TP37 文献标志码:A 文章编号:1673⁃4785(2016)01⁃0055⁃06 中文引用格式:方鹏,李贤,汪增福.运用核聚类和偏最小二乘回归的歌唱声音转换[J]. 智能系统学报, 2016, 11(1): 55⁃60. 英文引用格式:FANG Peng, LI Xian, WANG Zengfu. Conversion of singing voice based on kernel clustering and partial least squares regression[J]. CAAI Transactions on Intelligent Systems, 2016, 11(1): 55⁃60. Conversion of singing voice based on kernel clustering and partial least squares regression FANG Peng 1,2,3 , LI Xian 1,3 , WANG Zengfu 1,2,3 (1. Department of Automation, University of Science and Technology of China, Hefei 230027, China; 2. Institute of Intelligent Ma⁃ chines, Chinese Academy of Sciences, Hefei 230031, China; 3. National Engineering Laboratory of Speech and Language Information Processing, Hefei 230027, China) Abstract:Voice conversion is a popular topic in the field of computer hearing, and the application of singing voices to voice conversion is a relatively new research direction, which widens the application scope of voice conversion. When a training dataset is small, the conventional Gaussian mixture model (GMM) method may cause overfitting and insufficient utilization of music information. In this study, we propose a method for converting the voice timbre of a source singer into that of a target singer and employ fundamental frequency to improve the converted singing voice quality. We use kernel clustering and partial least squares regression to train the dataset, thereby obtaining the conversion function. To improve the converted singing voice quality, we applied the Mel log spectrum approxi⁃ mation (MLSA) filter, which synthesizes the converted singing voice by filtering the source singing waveform. Based on our experiment results, the proposed method demonstrates better voice similarity and quality, and there⁃ fore is a better choice than the GMM⁃based method when the training dataset is small. Keywords:computer vision; voice conversion; singing voice; kernel clustering; partial least squares regression; Gaussian mixture model; Mel log spectrum approximation 收稿日期:2015⁃06⁃11. 网络出版日期:2015⁃12⁃29. 基金项目:国家自然科学基金资助项目(61472393,613031350). 通信作者:汪增福.E⁃mail:zfwang@ ustc.edu.cn. 语音转换是一项非常热门的技术,在近 20 年间 开始涌现,它可以通过修饰一个源说话者的声音,在 不改变语义信息的情况下,使其声音听起来像是另 一个特定的人所说的。 由于每个人生理特征的限 制,使得我们在发音的时候不能自由的转换音色,只 能在某种程度上轻微地改变自己的音色,但是当说

·56. 智能系统学报 第11卷 话者想要使其声音变成另一个人的音色时存在很大 训练数据的时将会得到比基于GMM方法具有更高 的难度。然而语音转换技术可以突破这一限制,实 的精确性。 现任意人之间的音色转换。在语音转换方面,科研 这两年随着神经网络的迅速崛起,也有一些 工作者已经做了大量的工作,因此很多人开始寻找 人开始使用神经网络相关方法来做语音转换[9。 新的研究方向,将歌唱声音运用到语音转换中将会 尽管这些方法都取得了比较好的成果,但是与To 成为一门热门课题,而且这也是和音乐相关技术运 da的方法相比并未有显著的提升,而且都较为复 用的一种创新)。本文针对歌唱声音提出了一种 杂,效率偏低。在歌唱声音转换的实际应用中,由 转换的方法,以实现不同歌唱者音色之间的转换。 于歌唱声音的数据相比普通语音数据会少很多 到目前为止,已经有了很多种语音转换的方法, (有时候只有一首歌),在很多情况下不能获得大 其中一个非常经典的方法就是码本匹配[)】,它通过 量的歌唱声音数据,因此针对歌唱声音转换的实 对源声音特征的码本中心进行线性加权来实现转 际应用,本文采用偏最小二乘法来计算转换函数。 换。可是由于码本中心的数量限制,这样转换得到 另一方面为了提高数据统计的精度,采用核模糊 的声音特征被限制在一定范围内,使得转换后的声 聚类来对歌唱声音特征进行聚类,以此来获得高 音特征缺少多样性。针对这一问题,很多人都提出 精度的聚类结果。 了解决方法,其中基于高斯混合模型(GMM)的统计 当语音的频谱被转换完成之后,下一步要进行 方法[3]是最为经典的方法,也是目前最前沿的方 的是对语音进行合成。传统的合成方法是使用一个 法。此方法通过使用GMM来对声音特征进行统计 声码器对转换后的频谱和基频进行合成,以此来合 建模,并使用多个局部回归函数的线性组合来作为 成转换后的声音。可是相对于普通的语音来说,歌 转换函数。不过这种方法存在2个问题:帧间的不 唱声音的音质是一个更为重要的指标,因此需要采 连续和过平滑,这是由于在这个模型中未对帧间的 用一些新的方法来提高歌唱声音的声音质量。为了 关联性进行建模,从而导致在转换时出现帧与帧之 减小合成的误差,提高歌唱声音的音质,本文使用差 间的不连续:另外由于统计模型经常会忽略频谱的 分频谱的方法进行歌唱合成0!,但不同于文献[10] 细节信息,细节信息的缺失就自然导致了过平滑的 中的方法,我们不使用差分频谱来进行训练,因为这 出现。为了解决高斯混合模型中出现的2个问题, 样可能会带来误差,本文将直接使用源声音频谱特 Todats)提出了频谱参数轨迹的最大似然估计法。一 征进行训练。 方面,通过增加帧间的动态变量来描述帧间的相关 1 歌唱声音转换框架 性,动态变量的引入成功地解决了帧间不连续的问 题:另一方面通过构建频谱包络的全局变量来缓和 图1给出了本文歌唱声音转换的框架图。我们 过平滑问题。 采用SPTK以及STRAIGHT[]作为语音信号处理 尽管基于GMM方法的帧间不连续以及过平滑 工具。由于歌唱声音的音色体现在频谱包络上,故 问题在某种程度上被解决了,但是此转换方法依然 在歌唱声音转换中采用频谱包络作为声音特征进行 存在过拟合的问题。过拟合的出现是由于系统过于 训练以及转换。 复杂而训练数据不足所导致的,在基于GMM的方 歌唱声音转换通常分为两部分:训练和转换。 法中过拟合是在计算协方差矩阵时被引入的。为了 在训练阶段,首先采用核模糊k-均值聚类算法[2] 在训练数据过少时避免过拟合问题,可以采用对角 对输入的源声音特征进行聚类,得到的聚类结果为 阵来计算协方差矩阵。可是对角阵的使用又使得输 一个隶属度矩阵。对隶属度矩阵和目标歌唱声音特 入矢量的各维之间相互独立,从而导致了语音质量 征向量使用偏最小二乘回归算法经行训练,从而得 的下降。为了克服对角阵导致的变量独立性和过拟 到转换函数。在转换阶段,对于输入源歌唱声音特 合问题,E.Helander提出了使用偏最小二乘回归 征,计算其隶属度矩阵,将隶属度矩阵代入求得的转 (PLS)[来计算转换函数的方法,这一方法在少量 换函数中,从而计算出目标歌唱声音特征
话者想要使其声音变成另一个人的音色时存在很大 的难度。 然而语音转换技术可以突破这一限制,实 现任意人之间的音色转换。 在语音转换方面,科研 工作者已经做了大量的工作,因此很多人开始寻找 新的研究方向,将歌唱声音运用到语音转换中将会 成为一门热门课题,而且这也是和音乐相关技术运 用的一种创新[1] 。 本文针对歌唱声音提出了一种 转换的方法,以实现不同歌唱者音色之间的转换。 到目前为止,已经有了很多种语音转换的方法, 其中一个非常经典的方法就是码本匹配[2] ,它通过 对源声音特征的码本中心进行线性加权来实现转 换。 可是由于码本中心的数量限制,这样转换得到 的声音特征被限制在一定范围内,使得转换后的声 音特征缺少多样性。 针对这一问题,很多人都提出 了解决方法,其中基于高斯混合模型(GMM)的统计 方法[3⁃4]是最为经典的方法,也是目前最前沿的方 法。 此方法通过使用 GMM 来对声音特征进行统计 建模,并使用多个局部回归函数的线性组合来作为 转换函数。 不过这种方法存在 2 个问题:帧间的不 连续和过平滑,这是由于在这个模型中未对帧间的 关联性进行建模,从而导致在转换时出现帧与帧之 间的不连续;另外由于统计模型经常会忽略频谱的 细节信息,细节信息的缺失就自然导致了过平滑的 出现。 为了解决高斯混合模型中出现的 2 个问题, Toda [5]提出了频谱参数轨迹的最大似然估计法。 一 方面,通过增加帧间的动态变量来描述帧间的相关 性,动态变量的引入成功地解决了帧间不连续的问 题;另一方面通过构建频谱包络的全局变量来缓和 过平滑问题。 尽管基于 GMM 方法的帧间不连续以及过平滑 问题在某种程度上被解决了,但是此转换方法依然 存在过拟合的问题。 过拟合的出现是由于系统过于 复杂而训练数据不足所导致的,在基于 GMM 的方 法中过拟合是在计算协方差矩阵时被引入的。 为了 在训练数据过少时避免过拟合问题,可以采用对角 阵来计算协方差矩阵。 可是对角阵的使用又使得输 入矢量的各维之间相互独立,从而导致了语音质量 的下降。 为了克服对角阵导致的变量独立性和过拟 合问题,E. Helander 提出了使用偏最小二乘回归 (PLS) [6]来计算转换函数的方法,这一方法在少量 训练数据的时将会得到比基于 GMM 方法具有更高 的精确性。 这两年随着神经网络的迅速崛起,也有一些 人开始使用神经网络相关方法来做语音转换[7⁃9] 。 尽管这些方法都取得了比较好的成果,但是与 To⁃ da 的方法相比并未有显著的提升,而且都较为复 杂,效率偏低。 在歌唱声音转换的实际应用中,由 于歌唱声音的数据相比普通语音数据会少很多 (有时候只有一首歌) ,在很多情况下不能获得大 量的歌唱声音数据,因此针对歌唱声音转换的实 际应用,本文采用偏最小二乘法来计算转换函数。 另一方面为了提高数据统计的精度,采用核模糊 聚类来对歌唱声音特征进行聚类,以此来获得高 精度的聚类结果。 当语音的频谱被转换完成之后,下一步要进行 的是对语音进行合成。 传统的合成方法是使用一个 声码器对转换后的频谱和基频进行合成,以此来合 成转换后的声音。 可是相对于普通的语音来说,歌 唱声音的音质是一个更为重要的指标,因此需要采 用一些新的方法来提高歌唱声音的声音质量。 为了 减小合成的误差,提高歌唱声音的音质,本文使用差 分频谱的方法进行歌唱合成[10] ,但不同于文献[10] 中的方法,我们不使用差分频谱来进行训练,因为这 样可能会带来误差,本文将直接使用源声音频谱特 征进行训练。 1 歌唱声音转换框架 图 1 给出了本文歌唱声音转换的框架图。 我们 采用 SPTK 以及 STRAIGHT [11] 作为语音信号处理 工具。 由于歌唱声音的音色体现在频谱包络上,故 在歌唱声音转换中采用频谱包络作为声音特征进行 训练以及转换。 歌唱声音转换通常分为两部分:训练和转换。 在训练阶段,首先采用核模糊 k⁃均值聚类算法[12⁃13] 对输入的源声音特征进行聚类,得到的聚类结果为 一个隶属度矩阵。 对隶属度矩阵和目标歌唱声音特 征向量使用偏最小二乘回归算法经行训练,从而得 到转换函数。 在转换阶段,对于输入源歌唱声音特 征,计算其隶属度矩阵,将隶属度矩阵代入求得的转 换函数中,从而计算出目标歌唱声音特征。 ·56· 智 能 系 统 学 报 第 11 卷
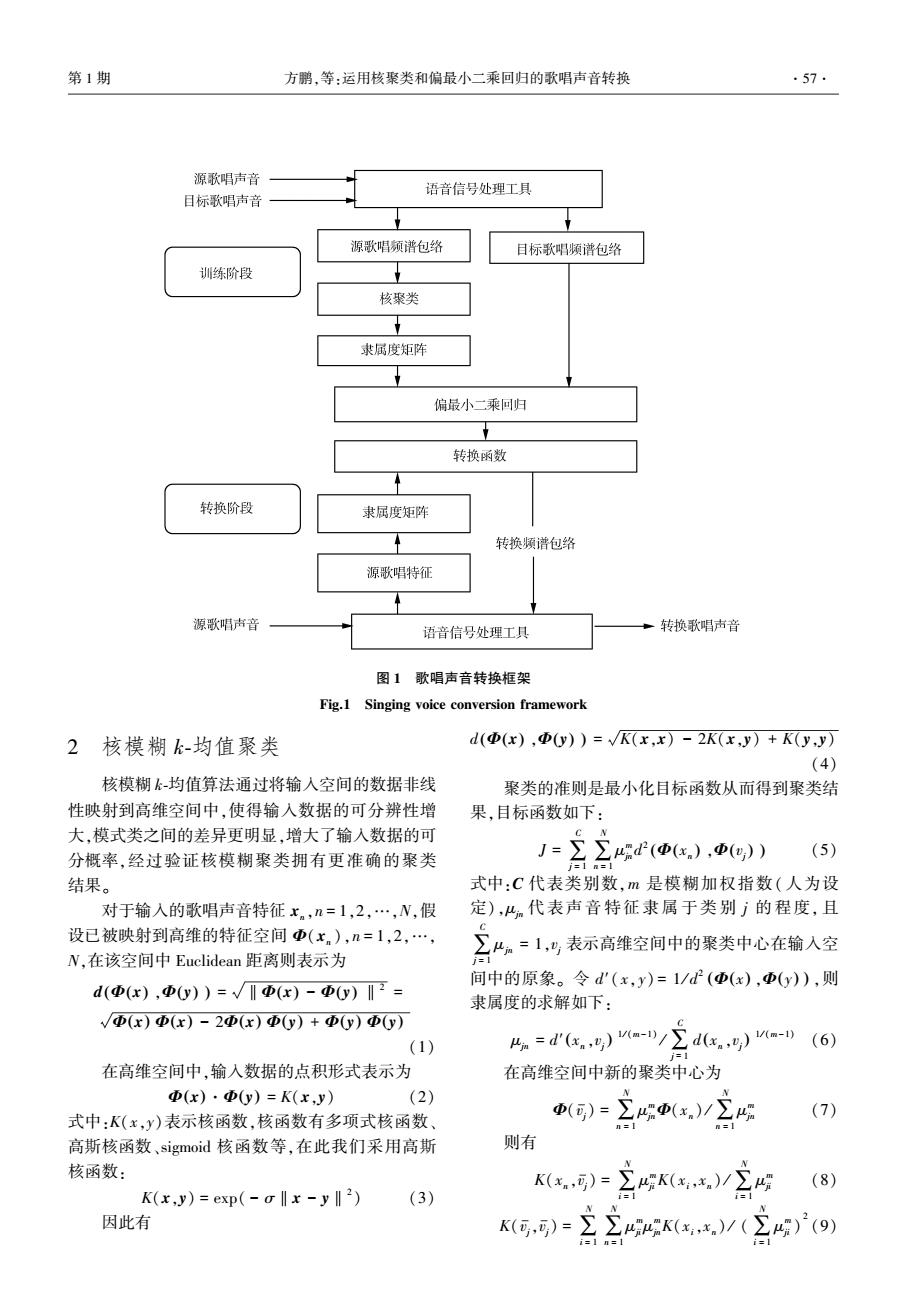
第1期 方鹏,等:运用核聚类和偏最小二乘回归的歌唱声音转换 ·57. 源歌唱声音 语音信号处理工具 目标歌唱声音 源歌唱颜谱包络 目标歌唱频谱包络 训练阶段 核聚类 隶属度矩阵 偏最小二乘回归 转换函数 转换阶段 隶属度矩阵 转换频谱包络 源歌唱特征 源歌唱声音 语音信号处理工具 转换歌唱声音 图1歌唱声音转换框架 Fig.1 Singing voice conversion framework 2核模糊k-均值聚类 d(④(x),Φy))=√K(x,x)-2K(x,y)+K(y,y) (4) 核模糊k-均值算法通过将输入空间的数据非线 聚类的准则是最小化目标函数从而得到聚类结 性映射到高维空间中,使得输入数据的可分辨性增 果,目标函数如下: 大,模式类之间的差异更明显,增大了输入数据的可 分概率,经过验证核模糊聚类拥有更准确的聚类 J=∑∑dP((x),(eg)) (5) =1 结果。 式中:C代表类别数,m是模糊加权指数(人为设 对于输入的歌唱声音特征x。,n=1,2,…,N,假 定),4n代表声音特征隶属于类别j的程度,且 设已被映射到高维的特征空间中(x),n=1,2,…, N,在该空间中Euclidean距离则表示为 三A,=1,表示高维空间中的聚类中心在输人空 间中的原象。令d'(x,y)=1/((x),(y)),则 d((x),心y))=√‖(x)-Dy)2= 隶属度的求解如下: √Φ(x)Φ(x)-2Φ(x)DGy)+DGy)Φy) (1) 4,=6.)-y2dkg)w(6 j=1 在高维空间中,输入数据的点积形式表示为 在高维空间中新的聚类中心为 (x)·Φ(y)=K(x,y) (2) 式中:K(x,y)表示核函数,核函数有多项式核函数、 (G)=立4(K,)/立 (7) 高斯核函数、sigmoid核函数等,在此我们采用高斯 则有 核函数: (8) K(x,y)=exp(-olx-yll2) (3) K)=25/g 因此有 K写》-言立AK(宫(9)
图 1 歌唱声音转换框架 Fig.1 Singing voice conversion framework 2 核模糊 k⁃均值聚类 核模糊 k⁃均值算法通过将输入空间的数据非线 性映射到高维空间中,使得输入数据的可分辨性增 大,模式类之间的差异更明显,增大了输入数据的可 分概率,经过验证核模糊聚类拥有更准确的聚类 结果。 对于输入的歌唱声音特征 xn ,n = 1,2,…,N,假 设已被映射到高维的特征空间 Φ( xn ),n = 1,2,…, N,在该空间中 Euclidean 距离则表示为 d(Φ(x) ,Φ(y) ) = ‖Φ(x) - Φ(y) ‖2 = Φ(x) Φ(x) - 2Φ(x) Φ(y) + Φ(y) Φ(y) (1) 在高维空间中,输入数据的点积形式表示为 Φ(x)·Φ(y) = K(x,y) (2) 式中:K(x,y)表示核函数,核函数有多项式核函数、 高斯核函数、sigmoid 核函数等,在此我们采用高斯 核函数: K(x,y) = exp( - σ‖x - y‖2 ) (3) 因此有 d(Φ(x) ,Φ(y) ) = K(x,x) - 2K(x,y) + K(y,y) (4) 聚类的准则是最小化目标函数从而得到聚类结 果,目标函数如下: J = ∑ C j = 1 ∑ N n = 1 μ m jn d 2 Φ xn ( ) ,Φ vj ( ( ) ) (5) 式中:C 代表类别数,m 是模糊加权指数(人为设 定),μjn 代表声音特征 隶 属 于 类 别 j 的 程 度, 且 ∑ C j = 1 μjn = 1,vj 表示高维空间中的聚类中心在输入空 间中的原象。 令 d′( x,y) = 1 / d 2 (Φ(x) ,Φ(y) ) ,则 隶属度的求解如下: μjn = d′ xn ,vj ( ) 1/ (m-1) /∑ C j = 1 d xn ,vj ( ) 1/ (m-1) (6) 在高维空间中新的聚类中心为 Φ(vj) = ∑ N n = 1 μ m jnΦ(xn ) /∑ N n = 1 μ m jn (7) 则有 K(xn ,vj) = ∑ N i = 1 μ m ji K(xi,xn ) /∑ N i = 1 μ m ji (8) K(vj,vj) = ∑ N i = 1 ∑ N n = 1 μ m ji μ m jnK(xi,xn ) / (∑ N i = 1 μ m ji ) 2 (9) 第 1 期 方鹏,等:运用核聚类和偏最小二乘回归的歌唱声音转换 ·57·

·58 智能系统学报 第11卷 更新隶属度: [k。kk+]T。那么根据偏最小二乘法有 y=Bk +e 通过对训练数据的训练则可以得到回归矩阵 (10) 循环迭代,直到maxl4n严nI<e或者迭代次数 B,对于任一输入歌唱声音特征,进行了核模糊k-均 值聚类后都可以通过B矩阵求得目标歌唱声音 等于预先设置的迭代次数。聚类结束后得到一个隶 特征。 属度矩阵K如下: K=[k:k2…kx] (11) 4 实验 式中:第n个列向量表示第n帧歌唱声音特征相对 4.1 客观实验 于C类的隶属度,即k=[h.he]T。对于求 对于客观实验的结果,我们使用转换后的Mcep 得的隶属度矩阵将要使用偏最小二乘法进行训练, 可是偏最小二乘法要求训练的对象是零均值的矩 (Mel-cepstral)系数与目标的Mcep系数的误差来描 述,具体计算公式如下所示: 阵,那么对于隶属度矩阵要进行零均值处理。 对K的每一行求均值,矩阵的每一行都减去该 10 24 S= 行的均值,这些行的均值保存在列向量”中。对于 n10 (c-c)2 (15) 每一列也进行相同的操作,但是不保存每一列的 式中:n表示任一帧,c。表示第n帧经转换得到的第 均值。 i个Mcep,对应的ci表示目标的第i个Mcep。 3偏最小二乘回归(PLS) 在这个实验中我们对比的是基于GMM模型的 方法,本文方法简称为KCPLS。对于GMM的方法 PLS(partial least squares regression)是一种结合 我们选择32个GMM,在KCPLS的方法中我们采用 了主成分分析和多元线性回归的技术,它非常适用 了具有400类的核聚类,核函数的σ参数值设为 于高维的数据,并且能够解决数据本身带来的共线 0.1。客观实验结果如表1所示。 性问题4。PLS有一个假设,源矢量x。是由一个 表1频谱平均误差 维度更低的矢量表示,并且这个矢量也可以生成目 Fig.1 The distortion of Mcep 标矢量y.。这个假设在歌唱声音转换中可以理解 dB 为:输入的源歌唱声音特征和输出的目标歌唱声音 方法 GMM KCPLS 特征可以由一个和说话者无关的歌唱声音特征所表 示。这个原理可以表示如下: 频谱误差 5.23 5.04 xn=Qr。+e (12) 如上表所示,基于KCPLS的方法相对于传统的 y=Pr +er (13) GMM方法能获得更准确的转换频谱,从而使得误差 式中:x。和y。分别表示源和目标的歌唱声音特征, 更小,转换的音色更相像。 ”.表示和说话者无关的向量,Q和P表示特定说话 4.2主观实验 人的转换矩阵,e和e表示残差项。由(12)、(13) 主观实验主要包括转换的相似度的主观实验和 可以看出,通过Q和P这两个矩阵可以得出x。和 转换合成后的歌唱声音质量的主观实验。由于传统 yn之间的一个关系式: 方法在声音合成上存在较大的误差,误差主要来自 y =Bx +e (14) 基频的提取、频谱的建模以及激励的合成,尤其是在 式中:B表示回归矩阵,是根据Q和P这两个矩阵 声音质量上可能会带来更大的误差。歌唱转换并不 求得的,en表示回归残差。 同于普通的语音转换,普通的语音转换要求在转换 由于单纯的线性回归转换的歌唱声音的相似性 频谱包络的同时也要转换基频,但是在歌唱声音的 以及质量都会下降,所以采用隶属度矩阵作为偏最 转换中却不需要,也不应该转换基频,这是由于每首 小二乘法的源数据特征,目标特征直接使用频谱特 歌都有其特定音高,而音高在某种程度上和基频有 征,从而间接建立了一个非线性转换,大大提高了转 着特定的关系,因此不建议转换基频。基频在提取 换的准确性。在歌唱声音转换中有一个很重要的一 以及用于合成声音时,会引起误差的存在,利用歌唱 项就是构建动态特征,我们通过拼接当前帧的前一 声音不需要转换基频的特性,用一种新的合成方法 帧和后一帧的隶属度来形成新的特征矢量k= 来提高歌唱声音的质量,即使用转换后的Mcep系
更新隶属度: ujn = d′ xn ,vj ( ) ) 1/ (m-1) /∑ C j = 1 d′ xn ,vj ( ) 1/ (m-1) (10) 循环迭代,直到max j,n | μjn -μjn | <ε 或者迭代次数 等于预先设置的迭代次数。 聚类结束后得到一个隶 属度矩阵 K 如下: K = k1 k2 … k [ N ] (11) 式中:第 n 个列向量表示第 n 帧歌唱声音特征相对 于 C 类的隶属度,即 kn = [μ1n μ2n… μCn ] Τ 。 对于求 得的隶属度矩阵将要使用偏最小二乘法进行训练, 可是偏最小二乘法要求训练的对象是零均值的矩 阵,那么对于隶属度矩阵要进行零均值处理。 对 K 的每一行求均值,矩阵的每一行都减去该 行的均值,这些行的均值保存在列向量 ν 中。 对于 每一列也进行相同的操作,但是不保存每一列的 均值。 3 偏最小二乘回归(PLS) PLS(partial least squares regression)是一种结合 了主成分分析和多元线性回归的技术,它非常适用 于高维的数据,并且能够解决数据本身带来的共线 性问题[14] 。 PLS 有一个假设,源矢量 xn 是由一个 维度更低的矢量表示,并且这个矢量也可以生成目 标矢量 yn 。 这个假设在歌唱声音转换中可以理解 为:输入的源歌唱声音特征和输出的目标歌唱声音 特征可以由一个和说话者无关的歌唱声音特征所表 示。 这个原理可以表示如下: xn = Qrn + e x n (12) yn = Prn + e y n (13) 式中:xn 和 yn 分别表示源和目标的歌唱声音特征, rn 表示和说话者无关的向量,Q 和 P 表示特定说话 人的转换矩阵,e x n 和 e y n 表示残差项。 由(12)、(13) 可以看出,通过 Q 和 P 这两个矩阵可以得出 xn 和 yn 之间的一个关系式: yn = βxn + en (14) 式中:β 表示回归矩阵,是根据 Q 和 P 这两个矩阵 求得的, en 表示回归残差。 由于单纯的线性回归转换的歌唱声音的相似性 以及质量都会下降, 所以采用隶属度矩阵作为偏最 小二乘法的源数据特征,目标特征直接使用频谱特 征,从而间接建立了一个非线性转换,大大提高了转 换的准确性。 在歌唱声音转换中有一个很重要的一 项就是构建动态特征,我们通过拼接当前帧的前一 帧和后一帧的隶属度来形成新的特征矢量 kn = [kn- kn kn+ ] Τ 。 那么根据偏最小二乘法有 yn = β kn + en 通过对训练数据的训练则可以得到回归矩阵 β,对于任一输入歌唱声音特征,进行了核模糊 k-均 值聚类后都可以通过 β 矩阵求得目标歌唱声音 特征。 4 实验 4.1 客观实验 对于客观实验的结果,我们使用转换后的 Mcep (Mel⁃cepstral)系数与目标的 Mcep 系数的误差来描 述,具体计算公式如下所示: S = 10 ln10 2∑ 24 i = 1 (c i n - c ~ i n ) 2 (15) 式中:n 表示任一帧,c ~ i n 表示第 n 帧经转换得到的第 i 个 Mcep,对应的 c i n 表示目标的第 i 个 Mcep。 在这个实验中我们对比的是基于 GMM 模型的 方法,本文方法简称为 KCPLS。 对于 GMM 的方法 我们选择 32 个 GMM,在 KCPLS 的方法中我们采用 了具有 400 类的核聚类,核函数的 σ 参数值设为 0.1。 客观实验结果如表 1 所示。 表 1 频谱平均误差 Fig.1 The distortion of Mcep dB 方法 GMM KCPLS 频谱误差 5.23 5.04 如上表所示,基于 KCPLS 的方法相对于传统的 GMM 方法能获得更准确的转换频谱,从而使得误差 更小,转换的音色更相像。 4.2 主观实验 主观实验主要包括转换的相似度的主观实验和 转换合成后的歌唱声音质量的主观实验。 由于传统 方法在声音合成上存在较大的误差,误差主要来自 基频的提取、频谱的建模以及激励的合成,尤其是在 声音质量上可能会带来更大的误差。 歌唱转换并不 同于普通的语音转换,普通的语音转换要求在转换 频谱包络的同时也要转换基频,但是在歌唱声音的 转换中却不需要,也不应该转换基频,这是由于每首 歌都有其特定音高,而音高在某种程度上和基频有 着特定的关系,因此不建议转换基频。 基频在提取 以及用于合成声音时,会引起误差的存在,利用歌唱 声音不需要转换基频的特性,用一种新的合成方法 来提高歌唱声音的质量,即使用转换后的 Mcep 系 ·58· 智 能 系 统 学 报 第 11 卷

第1期 方鹏,等:运用核聚类和偏最小二乘回归的歌唱声音转换 ·59 数与源Mcep系数的差值构建一个梅尔对数频谱 斯混合模型的方法中,由于协方差矩阵的使用,在训 (Mel log spectrum approximation)滤波器[],并且使 练数据不足的情况下,会出现过拟合的现象,严重影 用这个滤波器直接对源歌唱声音信号进行滤波,从 响声音的相似度和声音的质量,而偏最小二乘法却 而得到质量更高的歌唱声音。 没有这个缺点,客观实验的结果很大程度上说明了 主观实验要求实验人员听力等方面正常,无听 这个问题。 力相关方面的疾病,且对音乐有一定的鉴赏能力。 测试数据为10句中文歌唱声音,我们采用平均意见 5结束语 分(mean opinion score)为我们的统计指标,实验人 本文提出了一种基于核模糊k-均值聚类和偏最 员对歌曲进行打分,分数为1~5分,1分最差,5分 小二乘的歌唱声音转换方法。该方法避免了传统基 最好。所有打分结束后,对每种方法的分数进行统 于高斯混合模型方法的过拟合问题。同时,基于差 计,求均值及95%的置信区间。所得结果如图2 值的MLSA滤波器,大大提高了合成的歌唱声音质 所示。 量。实验采用中文歌唱声音进行转换,结果表明,新 5.0 方法在相似度以及声音质量上都要优于传统的基于 45 GWM 高斯混合模型的方法。尽管该方法目前取得了不错 4.0 KCPLS 的效果,但未来还会对该方法进行完善,下一步工作 3.0 是研究如何用完整的频谱包络代替梅尔倒谱系数进 2.5 行歌唱声音转换,期望未来能够取得更好的结果。 2.0 15 参考文献: 1.0 0.5 [1]VILLAVICENCIO F,BONADA J.Applying voice conver- 0 相似度 声音质量 sion to concatenative singing-voice synthesis[C//Proceed- ings of Interspeech.Chiba,Japan,2010:2162-2165. 图2相似度和声音质量的平均意见分及95%置信区间 [2]ABE M,NAKAMURA S.SHIKANO K,et al.Voice con- Fig.2 MOS(95%CIs)for similarity and quality version through vector quantization[].Journal of the acous- tical society japan (E),1990,11(2):71-76. 从图2的主观实验可以看出,在主观的相似度 [3]KAIN A,MACON M W.Spectral voice conversion for text- 实验方面,基于核模糊k-均值聚类和偏最小二乘法 to-speech synthesis[C]//Proceedings of the 1998 IEEE In- 的实验结果在听觉上获得了更高的相似度,MOS得 ternational Conference on Acoustics,Speech and Signal Pro- 分高了1.8分。在声音质量的主观实验上,基于频 cessing.Seattle,WA,USA.1998.1:285-288. 谱差值构建MLSA滤波器的方法能够合成质量更高 [4]STYLIANOU Y,CAPPE,O,MOULINES E.Continuous 的歌唱声音,MOS得分高出了1分。 probabilistic transform for voice conversion[J].IEEE trans- 4.3实验结果分析 actions on speech and audio processing,1998.6(2):131- 142. 客观实验和主观实验表明,相对于传统的基于 [5]TODA T,BLACK A W,TOKUDA K.Voice conversion 高斯混合模型的转换方法,基于核聚类和偏最小二 based on maximum-likelihood estimation of spectral parame- 乘法对歌唱声音的转换能够取得更高的准确度,实 ter trajectory[].IEEE transactions on audio,speech,and 验也证明了基于频谱差值构建MLSA滤波器的方 language processing,2007,15(8):2222-2235. 法,在提高合成的歌唱声音质量上有明显的优势。 [6]HELANDER E,VIRTANEN T,NURMINEN J,et al. 此外,相对于普通的语音来说,歌唱声音对声音的要 Voice conversion using partial least squares regression[J]. 求更高,而且某种程度上歌唱声音质量可能也会影 IEEE transactions on audio,speech,and language process- 响听者对于转换相似度的分辨。 ing,2010,18(5):912-921. 基于核模糊k-均值聚类和偏最小二乘回归的方 [7LIU Lijuan,CHEN Linghui,LING Zhenhua,et al.Using 法,通过使用核模糊k-均值聚类的方式引入了概率 bidirectional associative memories for joint spectral envelope modeling in voice conversion[C]//Proceedings of IEEE In- 隶属度矩阵,使得非线性转换在某种程度上以线性 ternational Conference on Acoustics,Speech and Signal Pro- 转换的形式实现,提高声音转换的准确性。在整个 cessing (ICASSP).Florence,Italy,2014:7884-7888. 算法的介绍中明显看出算法相比于传统的GMM模 [8]CHEN Linghui,LING Zhenhua,LIU Lijuan,et al.Voice 型复杂度低,以线性的形式实现非线性的形式。高 conversion using deep neural networks with layer-wise gener-
数与源 Mcep 系数的差值构建一个梅尔对数频谱 (Mel log spectrum approximation)滤波器[15] ,并且使 用这个滤波器直接对源歌唱声音信号进行滤波,从 而得到质量更高的歌唱声音。 主观实验要求实验人员听力等方面正常,无听 力相关方面的疾病,且对音乐有一定的鉴赏能力。 测试数据为 10 句中文歌唱声音,我们采用平均意见 分(mean opinion score)为我们的统计指标,实验人 员对歌曲进行打分,分数为 1 ~ 5 分,1 分最差,5 分 最好。 所有打分结束后,对每种方法的分数进行统 计,求均值及 95% 的置信区间。 所得结果如图 2 所示。 图 2 相似度和声音质量的平均意见分及 95%置信区间 Fig.2 MOS(95% CIs) for similarity and quality 从图 2 的主观实验可以看出,在主观的相似度 实验方面,基于核模糊 k⁃均值聚类和偏最小二乘法 的实验结果在听觉上获得了更高的相似度,MOS 得 分高了 1.8 分。 在声音质量的主观实验上,基于频 谱差值构建 MLSA 滤波器的方法能够合成质量更高 的歌唱声音,MOS 得分高出了 1 分。 4.3 实验结果分析 客观实验和主观实验表明,相对于传统的基于 高斯混合模型的转换方法,基于核聚类和偏最小二 乘法对歌唱声音的转换能够取得更高的准确度,实 验也证明了基于频谱差值构建 MLSA 滤波器的方 法,在提高合成的歌唱声音质量上有明显的优势。 此外,相对于普通的语音来说,歌唱声音对声音的要 求更高,而且某种程度上歌唱声音质量可能也会影 响听者对于转换相似度的分辨。 基于核模糊 k⁃均值聚类和偏最小二乘回归的方 法,通过使用核模糊 k⁃均值聚类的方式引入了概率 隶属度矩阵,使得非线性转换在某种程度上以线性 转换的形式实现,提高声音转换的准确性。 在整个 算法的介绍中明显看出算法相比于传统的 GMM 模 型复杂度低,以线性的形式实现非线性的形式。 高 斯混合模型的方法中,由于协方差矩阵的使用,在训 练数据不足的情况下,会出现过拟合的现象,严重影 响声音的相似度和声音的质量,而偏最小二乘法却 没有这个缺点,客观实验的结果很大程度上说明了 这个问题。 5 结束语 本文提出了一种基于核模糊 k⁃均值聚类和偏最 小二乘的歌唱声音转换方法。 该方法避免了传统基 于高斯混合模型方法的过拟合问题。 同时,基于差 值的 MLSA 滤波器,大大提高了合成的歌唱声音质 量。 实验采用中文歌唱声音进行转换,结果表明,新 方法在相似度以及声音质量上都要优于传统的基于 高斯混合模型的方法。 尽管该方法目前取得了不错 的效果,但未来还会对该方法进行完善,下一步工作 是研究如何用完整的频谱包络代替梅尔倒谱系数进 行歌唱声音转换,期望未来能够取得更好的结果。 参考文献: [1] VILLAVICENCIO F, BONADA J. Applying voice conver⁃ sion to concatenative singing⁃voice synthesis[C] / / Proceed⁃ ings of Interspeech. Chiba, Japan, 2010: 2162⁃2165. [2]ABE M, NAKAMURA S, SHIKANO K, et al. Voice con⁃ version through vector quantization[J]. Journal of the acous⁃ tical society japan (E), 1990, 11(2): 71⁃76. [3]KAIN A, MACON M W. Spectral voice conversion for text⁃ to⁃speech synthesis[C] / / Proceedings of the 1998 IEEE In⁃ ternational Conference on Acoustics, Speech and Signal Pro⁃ cessing. Seattle, WA, USA, 1998, 1: 285⁃288. [4] STYLIANOU Y, CAPPE, O, MOULINES E. Continuous probabilistic transform for voice conversion[J]. IEEE trans⁃ actions on speech and audio processing, 1998, 6(2): 131⁃ 142. [5] TODA T, BLACK A W, TOKUDA K. Voice conversion based on maximum⁃likelihood estimation of spectral parame⁃ ter trajectory[J]. IEEE transactions on audio, speech, and language processing, 2007, 15(8): 2222⁃2235. [ 6 ] HELANDER E, VIRTANEN T, NURMINEN J, et al. Voice conversion using partial least squares regression[J]. IEEE transactions on audio, speech, and language process⁃ ing, 2010, 18(5): 912⁃921. [7]LIU Lijuan, CHEN Linghui, LING Zhenhua, et al. Using bidirectional associative memories for joint spectral envelope modeling in voice conversion[C] / / Proceedings of IEEE In⁃ ternational Conference on Acoustics, Speech and Signal Pro⁃ cessing (ICASSP). Florence, Italy, 2014: 7884⁃7888. [8]CHEN Linghui, LING Zhenhua, LIU Lijuan, et al. Voice conversion using deep neural networks with layer⁃wise gener⁃ 第 1 期 方鹏,等:运用核聚类和偏最小二乘回归的歌唱声音转换 ·59·

·60 智能系统学报 第11卷 ative training [J ]IEEE/ACM Transactions on audio, [15]IMAI S,SUMITA K,FURUICHI C.Mel log spectrum ap- speech,and language processing,2014,22(12):1859- proximation (MISA)filter for speech synthesis[J].Elec- 1872. tronics and communications in Japan (Part I:Communica- [9]DESAI S,BLACK A W,YEGNANARAYANA B,et al. tions),1983,66(2):10-18 Spectral mapping using artificial neural networks for voice 作者简介: conversion[J].IEEE transactions on audio,speech,and 方鹏,男,1990年生,硕士研究生 language processing,2010,18(5):954-964. 主要研究方向为歌唱声音转换。 [10]KOBAYASHI K,TODA T,NEUBIG G,et al.Statistical singing voice conversion with direct waveform modification based on the spectrum differential[C]//Proceedings of In- terspeech.Singapore,2014. [11]KAWAHARA H,MORISE M,TAKAHASHI T,et al. Tandem-STRAIGHT:A temporally stable power spectral representation for periodic signals and applications to in- 李贤,男,1988年生,博士研究生, terference-free spectrum,F0,and aperiodicity estimation 主要研究方向为情感语音、语音转换、 [C]//Proceedings of IEEE International Conference on 歌唱合成等。 Acoustics,Speech and Signal Processing,ICASSP.Las Vegas,.NV,USA,2008:3933-3936. [12]WU Zhongdong,XIE Weixin,YU Jianping.Fuzzy C- means clustering algorithm based on kernel method[C]/ Proceedings of the 5"International Conference on Compu- tational Intelligence and Multimedia Applications.ICCI- 汪增福,男,1960年生,教授、博士 MA.Xi'an,China,2003:49-54. 生导师,现任《模式识别与人工智能》编 [13]GRAVES D,PEDRYCZ W.Kernel-based fuzzy clustering 委、International Journal of Information and fuzzy clustering:a comparative experimental study[J]. Acquisition副主编。获ACM Multimedia Fuzzy Sets Systems,2010,161(4):522-543. 2009最佳论文奖。主要研究方向为计 [14]DE JONG S.SIMPLS:An alternative approach to partial 算机视觉、计算机听觉、人机交互和智 least squares regression[J].Chemometrics and intelligent 能机器人等,发表学术论文180余篇。 laboratory systems,1993,18(3):251-263
ative training [ J ]. IEEE/ ACM Transactions on audio, speech, and language processing, 2014, 22 ( 12): 1859⁃ 1872. [9] DESAI S, BLACK A W, YEGNANARAYANA B, et al. Spectral mapping using artificial neural networks for voice conversion[ J]. IEEE transactions on audio, speech, and language processing, 2010, 18(5): 954⁃964. [10]KOBAYASHI K, TODA T, NEUBIG G, et al. Statistical singing voice conversion with direct waveform modification based on the spectrum differential[C] / / Proceedings of In⁃ terspeech. Singapore, 2014. [11] KAWAHARA H, MORISE M, TAKAHASHI T, et al. Tandem⁃STRAIGHT: A temporally stable power spectral representation for periodic signals and applications to in⁃ terference⁃free spectrum, F0, and aperiodicity estimation [C] / / Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP. Las Vegas, NV, USA, 2008: 3933⁃3936. [12] WU Zhongdong, XIE Weixin, YU Jianping. Fuzzy C - means clustering algorithm based on kernel method[C] / / Proceedings of the 5 th International Conference on Compu⁃ tational Intelligence and Multimedia Applications. ICCI⁃ MA. Xian, China, 2003: 49⁃54. [13]GRAVES D, PEDRYCZ W. Kernel⁃based fuzzy clustering and fuzzy clustering: a comparative experimental study[J]. Fuzzy Sets Systems, 2010, 161(4): 522⁃543. [14]DE JONG S. SIMPLS: An alternative approach to partial least squares regression[ J]. Chemometrics and intelligent laboratory systems, 1993, 18(3): 251⁃263. [15]IMAI S, SUMITA K, FURUICHI C. Mel log spectrum ap⁃ proximation (MLSA) filter for speech synthesis[ J]. Elec⁃ tronics and communications in Japan (Part I: Communica⁃ tions), 1983, 66(2): 10⁃18. 作者简介: 方鹏,男,1990 年生,硕士研究生, 主要研究方向为歌唱声音转换。 李贤,男,1988 年生,博士研究生, 主要研究方向为情感语音、语音转换、 歌唱合成等。 汪增福,男,1960 年生,教授、博士 生导师,现任《模式识别与人工智能》编 委、 International Journal of Information Acquisition 副主编。 获 ACM Multimedia 2009 最佳论文奖。 主要研究方向为计 算机视觉、计算机听觉、人机交互和智 能机器人等,发表学术论文 180 余篇。 ·60· 智 能 系 统 学 报 第 11 卷