
第11卷第2期 智能系统学报 Vol.11 No.2 2016年4月 CAAI Transactions on Intelligent Systems Apr.2016 D0I:10.11992/is.201507064 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160315.1239.012.html 分段聚合近似和数值导数的动态时间弯曲方法 李海林,梁叶 (华侨大学信息管理系,福建泉州362021)》 摘要:针对动态弯曲方法对时间序列数据相似性度量的质量和效率的局限性,本文提出一种基于分段聚合近似和 数值导数的动态时间弯曲方法。该方法通过分段聚合近似将时间序列数据进行有效地降维,再结合数值导数对降 维后的特征序列构建新特征序列,并且设计符合该特征序列相似性度量方法。实验结果分析表明,与传统动态弯曲 方法相比,新方法具有较好的度量质量,能在时间序列数据挖掘中得到较好的分类效果,且在低维空间具有较高的 分类效率,具有一定的优越性。 关键词:动态时间弯曲;时间序列:分段聚合近似;数值导数:相似性度量:分类:数据降维:特征表示 中图分类号:TP301文献标志码:A文章编号:1673-4785(2016)02-0249-08 中文引用格式:李海林,梁叶.分段聚合近似和数值导数的动态时间弯曲方法[J】.智能系统学报,2016,11(2):249-256. 英文引用格式:LI Hailin,LIANG Ye.Dynamic time warping based on piecewise aggregate approximation and data derivatives[J]. CAAI transactions on intelligent systems,2016,11(2):249-256. Dynamic time warping based on piecewise aggregate approximation and data derivatives LI Hailin,LIANG Ye (Department of Information Management,Huaqiao University,Quanzhou 362021,China) Abstract:Dynamic time warping(DTW)is often used to measure the similarity of time series data;however,it has efficiency and quality limitations.In this study,a novel DTW method combining piecewise aggregate approximation (PAA)and derivatives is proposed to measure the similarity of time series.The dimensionality of the time series data was effectively reduced by PAA,and the feature sequence was transformed into new sequences by combining the numerical derivatives after the dimensionality reduction.Furthermore,the DTW design corresponded to the sim- ilarity measurement method of the feature sequence.The experimental results demonstrate that the proposed method is superior because it has better measurement quality,obtains a better classification effect in time series data min- ing,and has high efficiency in lower dimensional spaces. Keywords:dynamic time warping;time series;piecewise aggregate approximation;numerical derivative;similari- ty measure;classification;dimensionality reduction;feature representation 近年来,时间序列成为了数据挖掘研究领域中 极其关键的工作之一,很多挖掘任务的结果易受其 的热点,其研究成果已被广泛地应用在工业、金融、 相似性度量质量和效率的影响。目前,动态时间弯 气象、航天、生物医学等各种领域]。然而,相似 曲(dynamic time warping,DTW)是一种鲁棒性较强 性度量方法成为时间序列数据挖掘领域中基础而又的方法之一,其最早应用于语音识别6,如今已被 广泛应用于时间序列相似性的度量[]。欧氏距离 收稿日期:2015-07-24.网络出版日期:2016-03-15. 基金项目:国家自然科学基金项目(61300139):福建省中青年教育科研 虽能快速度量时间序列之间的相似性,但其限于相 基金项目(JAS14024):华侨大学中青年教师科研提升计划项 同时间点上的数据匹配,而且对异常数据点较为敏 目(ZQN-PY220). 通信作者:李海林.E-mail:hailin(@hqu.cdu.cn 感。DTW不仅可以弯曲度量不等长时间序列之间
第 11 卷第 2 期 智 能 系 统 学 报 Vol.11 №.2 2016 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2016 DOI:10.11992 / tis.201507064 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160315.1239.012.html 分段聚合近似和数值导数的动态时间弯曲方法 李海林,梁叶 (华侨大学 信息管理系, 福建 泉州 362021) 摘 要:针对动态弯曲方法对时间序列数据相似性度量的质量和效率的局限性,本文提出一种基于分段聚合近似和 数值导数的动态时间弯曲方法。 该方法通过分段聚合近似将时间序列数据进行有效地降维,再结合数值导数对降 维后的特征序列构建新特征序列,并且设计符合该特征序列相似性度量方法。 实验结果分析表明,与传统动态弯曲 方法相比,新方法具有较好的度量质量,能在时间序列数据挖掘中得到较好的分类效果,且在低维空间具有较高的 分类效率,具有一定的优越性。 关键词:动态时间弯曲;时间序列;分段聚合近似;数值导数;相似性度量;分类;数据降维;特征表示 中图分类号: TP301 文献标志码:A 文章编号:1673⁃4785(2016)02⁃0249⁃08 中文引用格式:李海林,梁叶. 分段聚合近似和数值导数的动态时间弯曲方法[J]. 智能系统学报, 2016, 11(2): 249⁃256. 英文引用格式:LI Hailin, LIANG Ye. Dynamic time warping based on piecewise aggregate approximation and data derivatives[J]. CAAI transactions on intelligent systems, 2016, 11(2): 249⁃256. Dynamic time warping based on piecewise aggregate approximation and data derivatives LI Hailin, LIANG Ye (Department of Information Management, Huaqiao University, Quanzhou 362021, China) Abstract:Dynamic time warping (DTW) is often used to measure the similarity of time series data; however, it has efficiency and quality limitations. In this study, a novel DTW method combining piecewise aggregate approximation (PAA) and derivatives is proposed to measure the similarity of time series. The dimensionality of the time series data was effectively reduced by PAA, and the feature sequence was transformed into new sequences by combining the numerical derivatives after the dimensionality reduction. Furthermore, the DTW design corresponded to the sim⁃ ilarity measurement method of the feature sequence. The experimental results demonstrate that the proposed method is superior because it has better measurement quality, obtains a better classification effect in time series data min⁃ ing, and has high efficiency in lower dimensional spaces. Keywords: dynamic time warping; time series; piecewise aggregate approximation; numerical derivative; similari⁃ ty measure; classification;dimensionality reduction; feature representation 收稿日期:2015⁃07⁃24. 网络出版日期:2016⁃03⁃15. 基金项目:国家自然科学基金项目(61300139);福建省中青年教育科研 基金项目(JAS14024);华侨大学中青年教师科研提升计划项 目(ZQN⁃PY220). 通信作者:李海林. E⁃mail:hailin@ hqu.edu.cn. 近年来,时间序列成为了数据挖掘研究领域中 的热点,其研究成果已被广泛地应用在工业、金融、 气象、航天、生物医学等各种领域[1⁃5] 。 然而,相似 性度量方法成为时间序列数据挖掘领域中基础而又 极其关键的工作之一,很多挖掘任务的结果易受其 相似性度量质量和效率的影响。 目前,动态时间弯 曲(dynamic time warping, DTW)是一种鲁棒性较强 的方法之一,其最早应用于语音识别[6] ,如今已被 广泛应用于时间序列相似性的度量[7⁃9] 。 欧氏距离 虽能快速度量时间序列之间的相似性,但其限于相 同时间点上的数据匹配,而且对异常数据点较为敏 感。 DTW 不仅可以弯曲度量不等长时间序列之间

·250· 智能系统学报 第11卷 的相似性,其度量质量能较好地反映数据之间的异 在减小数据存储和提高计算效率方面起到了很大的 步关系[o]。然而,由于DTW需要在代价矩阵中计 作用。通过对长度为n的序列S=(s1,s2,…,sn)转 算最优弯曲路径,使其具有较高的时间复杂度或较 化为另一条长度为m的序列Q=(q1,92,…,9m), 好的度量精度[)。 实现时间序列的数据降维和特征表示,其中n>m, 时间序列降维表示是通过某种方法将原始序列 且令k=n/m。新序列中任意元素q:满足: 进行转换或者特征提取,以达到将原始时间序列在 低维度表示的目的。由于直接使用和计算原始时间 1≤i≤m(1) 序列可能需要付出较大的代价,如消耗较多存储空 对序列S进行分段后求出每段的均值,每段均值 间,运行效率低等问题,加上原始时间序列包含很多 形成序列Q,进而达到序列S数据降维的目的。如图 “噪音点”,容易导致相似性度量结果不准确。因 1,子图(a)显示了长度为60的时间序列S通过PAA 此,为简化数据模型和算法的复杂性,提高数据挖掘 被平均分成10段,每段均值代表相应片段的特征:子 技术的性能,有必要对原始时间序列进行降维处理, 图(b)显示由10个均值组成的新序列Q。 达到效率和准确性的平衡。目前,针对时间序列降 2 1.0 维的方法已有很多且较为成熟,如分段聚合近似 (piecewise aggregate approximation,PAA)【],该方 法通过将时间序列进行平均分段,并以分段均值反 映分段信息,最终达到数据降维的目的:分段线性近 似(piecewise liner approximation,PLA)【I利用线性 -1.0 模型对时间序列进行分割,根据不同的分割策略可 2040 60 246810 时间戳/s 时间戳/s 以得到不同的时间序列降维效果:基于域变换的离 (a)时间序列及其分段均值 (b)时间序列的特征表示 散傅里叶变换(discrete fourier transform,DFT)【u6和 图1基于PAA的时间序列数据降维和特征表示 离散小波变换(discrete wavelet transform, Fig.1 Dimensionality reduction and feature represen- DWT)【1),利用变换后的系数对时间序列进行特征 tation of time series based on PAA 表示;奇异值分解(singular value decomposition, 分段聚合近似方法通过均值来表示序列片段的 SVD)[1),利用数值计算将高维数据转换到低维空 特征,容易忽略数据的局部形态变化情况。然而,在 间,不仅应用在时间序列数据降维及索引,而且也被 实际运用中,时间序列的整体形态通常是关注和研 广泛地应用于模式识别、图像压缩等等。由于降维 究的重点。PAA得到的序列特征不仅能够很好地 方法对整个研究过程起着十分关键的作用,不仅要 反映较长时间序列数据形态的整体变化趋势,而且 求算法能够尽可能简单快速,以降低时间消耗,也要 还能对时间序列数据进行数据降维,起到提高相关 尽量充分反映时间序列的信息。因此研究过程中应 数据挖掘算法效率的作用。 选择合适的降维方法来解决问题。 1.2动态时间弯曲 鉴于传统DTW方法在度量时间序列相似性时 动态时间弯曲最初被应用于语音识别中,常被 具有计算时间效率较低和缺少考虑序列的形态(即 运用到比较2条时间序列的相似性。针对2条时间 凹凸性)等问题,并且从使用较为简单的数据降维 方法以简化模型的角度出发,本文提出通过利用分 序列S=(s1s2,…,sn)和Q=(91,92,…,9m),对任 意两点之间的距离构建一个n×m的距离矩阵D, 段聚合近似(PAA)方法对时间序列进行数据降维, 获得保持原始序列主要特征的数据序列,再构造基 其中d(i,)表示时间序列数据点s:和g之间的距 于数据点的一阶导数的新特征序列,结合动态时间 离,即d(i,)=(s:-g)。DTW的基本思想就是从 弯曲提出一种新的距离度量方法,即近似导数动态 距离矩阵中寻找一条使得2条序列之间的累计距离 时间弯曲方法。数值实验分类结果和效率分析表 最小的路径,其最小累积距离值为 明,该方法能从形态视角出发,较好地从数据集中找 DTw(s.)=min() (2) 出相似序列,提高数据挖掘领域中分类算法的质量, 具有一定的优越性。 弯曲路径是一条具有连续K个距离矩阵元素 的集合W=(01,w2,…,0x),第k个元素为0g= 1 相关理论基础 (i,j)k且max(n,m)≤K≤n+m-1。与此同时, 1.1分段聚合近似(PAA) 弯曲路径通常要遵循着3个条件: 分段聚合近似是一种有效的数据降维方法,其 1)边界性:w1=(1,1),0k=(n,m);
的相似性,其度量质量能较好地反映数据之间的异 步关系[10] 。 然而,由于 DTW 需要在代价矩阵中计 算最优弯曲路径,使其具有较高的时间复杂度或较 好的度量精度[11⁃13] 。 时间序列降维表示是通过某种方法将原始序列 进行转换或者特征提取,以达到将原始时间序列在 低维度表示的目的。 由于直接使用和计算原始时间 序列可能需要付出较大的代价,如消耗较多存储空 间,运行效率低等问题,加上原始时间序列包含很多 “噪音点”,容易导致相似性度量结果不准确。 因 此,为简化数据模型和算法的复杂性,提高数据挖掘 技术的性能,有必要对原始时间序列进行降维处理, 达到效率和准确性的平衡。 目前,针对时间序列降 维的方法已有很多且较为成熟,如分段聚合近似 (piecewise aggregate approximation, PAA) [14] ,该方 法通过将时间序列进行平均分段,并以分段均值反 映分段信息,最终达到数据降维的目的;分段线性近 似(piecewise liner approximation, PLA) [15]利用线性 模型对时间序列进行分割,根据不同的分割策略可 以得到不同的时间序列降维效果;基于域变换的离 散傅里叶变换(discrete fourier transform, DFT) [16]和 离 散 小 波 变 换 ( discrete wavelet transform, DWT) [17] ,利用变换后的系数对时间序列进行特征 表示; 奇 异 值 分 解 ( singular value decomposition, SVD) [18] ,利用数值计算将高维数据转换到低维空 间,不仅应用在时间序列数据降维及索引,而且也被 广泛地应用于模式识别、图像压缩等等。 由于降维 方法对整个研究过程起着十分关键的作用,不仅要 求算法能够尽可能简单快速,以降低时间消耗,也要 尽量充分反映时间序列的信息。 因此研究过程中应 选择合适的降维方法来解决问题。 鉴于传统 DTW 方法在度量时间序列相似性时 具有计算时间效率较低和缺少考虑序列的形态(即 凹凸性)等问题,并且从使用较为简单的数据降维 方法以简化模型的角度出发,本文提出通过利用分 段聚合近似(PAA)方法对时间序列进行数据降维, 获得保持原始序列主要特征的数据序列,再构造基 于数据点的一阶导数的新特征序列,结合动态时间 弯曲提出一种新的距离度量方法,即近似导数动态 时间弯曲方法。 数值实验分类结果和效率分析表 明,该方法能从形态视角出发,较好地从数据集中找 出相似序列,提高数据挖掘领域中分类算法的质量, 具有一定的优越性。 1 相关理论基础 1.1 分段聚合近似(PAA) 分段聚合近似是一种有效的数据降维方法,其 在减小数据存储和提高计算效率方面起到了很大的 作用。 通过对长度为 n 的序列 S = (s1 ,s2 ,…,sn ) 转 化为另一条长度为 m 的序列 Q = (q1 ,q2 ,…,qm ) , 实现时间序列的数据降维和特征表示,其中 n > m , 且令 k = n / m 。 新序列中任意元素 qi 满足: qi = 1 k ∑ k∗i j = k∗(i-1) +1 si, 1 ≤ i ≤ m (1) 对序列 S 进行分段后求出每段的均值,每段均值 形成序列 Q ,进而达到序列 S 数据降维的目的。 如图 1,子图(a)显示了长度为 60 的时间序列 S 通过 PAA 被平均分成 10 段,每段均值代表相应片段的特征;子 图(b)显示由 10 个均值组成的新序列 Q 。 图 1 基于 PAA 的时间序列数据降维和特征表示 Fig.1 Dimensionality reduction and feature represen⁃ tation of time series based on PAA 分段聚合近似方法通过均值来表示序列片段的 特征,容易忽略数据的局部形态变化情况。 然而,在 实际运用中,时间序列的整体形态通常是关注和研 究的重点。 PAA 得到的序列特征不仅能够很好地 反映较长时间序列数据形态的整体变化趋势,而且 还能对时间序列数据进行数据降维,起到提高相关 数据挖掘算法效率的作用。 1.2 动态时间弯曲 动态时间弯曲最初被应用于语音识别中,常被 运用到比较 2 条时间序列的相似性。 针对 2 条时间 序列 S = (s1 ,s2 ,…,sn ) 和 Q = (q1 ,q2 ,…,qm ) ,对任 意两点之间的距离构建一个 n × m 的距离矩阵 D , 其中 d(i,j) 表示时间序列数据点 si 和 qj 之间的距 离,即 d(i,j) = (si - qj) 2 。 DTW 的基本思想就是从 距离矩阵中寻找一条使得 2 条序列之间的累计距离 最小的路径,其最小累积距离值为 DTW(S,Q) = min W (∑ K k = 1 wk) (2) 弯曲路径是一条具有连续 K 个距离矩阵元素 的集合 W = (w1 ,w2 ,…,wK ) ,第 k 个元素为 wk = (i,j)k 且 max(n,m) ≤ K ≤ n + m - 1。 与此同时, 弯曲路径通常要遵循着 3 个条件: 1)边界性: w1 = (1,1) , wk = (n,m) ; ·250· 智 能 系 统 学 报 第 11 卷

第2期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 ·251· 2)连续性:0g=(a,b),Wg-1=(a',b'),则 (s:-g)?;DDTW距离矩阵元素的距离值为对应导 a-a'≤1,b-b'≤1; 数之间的距离,即d(i,》=(s'-g)之,且数值导数 3)单调性:w4=(a,b),0x-1=(a',b'),则 s':为 a-a'≥0,b-b'≥0: 最优弯曲路径的求解可以通过动态规划来找出 ,=-5-)+(1-1)2 (4) 2 最小累积距离,即 [y(i-1,j-1) 2近似导数动态时间弯曲方法 y(i,j)=d(i,j)+miny(i-1,j) (3) 若直接使用动态时间弯曲方法对时间序列进行 y(i,j-1) 相似性度量,则时间消耗太大,并且也会造成时间过 式(3)说明当前元素的累积距离(i,)是当前 度弯曲等问题,不利于大规模的长度较长的时间序 元素距离值与邻近3个元素累积距离的最小值之 列数据挖掘。为此,在使用动态时间弯曲度量相似 和,且y(n,m)表示DTW度量时间序列S和Q的最 性之前,通常先对时间序列数据进行数据降维,不仅 小距离DTW(S,Q)=y(n,m)。 可以得到反映时间序列大部分信息的低维特征表 如图2(a)所示,动态时间弯曲方法可以很好地 示,而且还能近似表示原始时间序列的整体性信息。 匹配不同时间点但具有相似形态的序列特征,使得 除此之外,在分类过程中,针对低频时间序列数据缺 时间序列的相似性特征能够较好地得到体现。另 少具体局部信息的状况,序列被归为哪一类通常可 外,通过累积矩阵的构建可以获取其最优弯曲路径 能取决于其整体形状,而不是局限于严格的数值比 和最小度量距离,如图2(b)所示。 较。因此,相似性度量的结果不仅需要充分考虑序 列的具体数值,也要考虑序列整体形态(凹凸性)。 传统研究方法是对时间序列进行数据降维,然 后使用传统距离公式直接进行相似性度量。由于数 据降维会损耗时间序列的部分信息,实验效果也就 46 10 12 相当于以准确性来换取时间效率。鉴于时间序列具 时间戳/s 体数据值的重要性、形态的特殊性、度量准确性以及 (a)动态时间弯曲 高运行效率的必要性,结合分段聚合近似以及数值 导数,提出一种基于分段聚合近似和数值导数的动 态时间弯曲方法,称为分段聚合导数距离(piecewise approximation derivative distance,PADD)。该方法 主要综合考虑时间序列的具体数值信息和形态特 征,以获得更好的度量效果,提高运行效率,减少异 常点对度量的影响为目标,同时从时间序列的整体 (b)最优路径 数据匹配和形态的凸凹性出发,更为完善地度量时 图2动态时间弯曲及其最优路径 间序列异步相关性。 Fig.2 Dynamic time warping and the best path 时间序列S=(s1,52,…,5n)和Q=(91,92,…, DTW在很多领域的应用中都有着很好的效果, 9m),通过分段聚合近似方法对它们进行数据降维 然而较高的时间复杂度成为了该方法的瓶颈问题。 并进行整体数据的特征表示,即S=PAA(S,w,)和 目前也有部分学者对其进行了改进,使其具有较好 Q=PAA(Q,D,),其中0,和w,为降维后维度,也是 的度量效率。另外,由于DTW有时也存在过度“变 分段数目。另外,为了反映原始时间序列整体形态 态”弯曲的状况,即一条时间序列的一个值对应着 的特征,利用数据导数来反映PAA对原始时间序列 另一条序列的较长子序列,进而造成计算结果不精 降维后的序列进行整体形态特征描述。利用式(4) 确的问题。针对该问题,Keogh和Pazzani提出了导 数动态时间弯曲(DDTW),有效地克服了DTW对时 对S和Q进行数据导数计算,以反映原始时间序列 间轴的过度弯曲时造成的影响。 的整体形态特征,即S”和Q'。最后,利用动态时间 DDTW与DTW两种方法基本算法相似,DTW 弯曲方法分别对(S,Q)和(S”,Q')进行距离度 中距离矩阵元素(i,)的距离值为d(i,)= 量,并综合两者的加权平均作为新方法的距离度量
2)连续性: wk = (a,b) , wK - 1 = (a′,b′) ,则 a -a′ ≤ 1, b - b′ ≤ 1; 3)单调性: wk = (a,b) , wK - 1 = (a′,b′) ,则 a -a′ ≥ 0, b - b′ ≥ 0; 最优弯曲路径的求解可以通过动态规划来找出 最小累积距离,即 γ(i,j) = d(i,j) + min γ(i - 1,j - 1) γ(i - 1,j) γ(i,j - 1) ì î í ïï ïï (3) 式(3)说明当前元素的累积距离 (i,j) 是当前 元素距离值与邻近 3 个元素累积距离的最小值之 和,且 γ(n,m) 表示 DTW 度量时间序列 S 和 Q 的最 小距离 DTW(S,Q) = γ(n,m) 。 如图 2(a)所示,动态时间弯曲方法可以很好地 匹配不同时间点但具有相似形态的序列特征,使得 时间序列的相似性特征能够较好地得到体现。 另 外,通过累积矩阵的构建可以获取其最优弯曲路径 和最小度量距离,如图 2(b)所示。 图 2 动态时间弯曲及其最优路径 Fig.2 Dynamic time warping and the best path DTW 在很多领域的应用中都有着很好的效果, 然而较高的时间复杂度成为了该方法的瓶颈问题。 目前也有部分学者对其进行了改进,使其具有较好 的度量效率。 另外,由于 DTW 有时也存在过度“变 态”弯曲的状况,即一条时间序列的一个值对应着 另一条序列的较长子序列,进而造成计算结果不精 确的问题。 针对该问题,Keogh 和 Pazzani 提出了导 数动态时间弯曲(DDTW),有效地克服了 DTW 对时 间轴的过度弯曲时造成的影响。 DDTW 与 DTW 两种方法基本算法相似,DTW 中距 离 矩 阵 元 素 (i,j) 的 距 离 值 为 d(i,j) = (si - qj) 2 ;DDTW 距离矩阵元素的距离值为对应导 数之间的距离,即 d(i,j) = (si ′ - qj ′) 2 ,且数值导数 s′i 为 s′i = (si - si-1 ) + (si+1 - si-1 ) / 2 2 (4) 2 近似导数动态时间弯曲方法 若直接使用动态时间弯曲方法对时间序列进行 相似性度量,则时间消耗太大,并且也会造成时间过 度弯曲等问题,不利于大规模的长度较长的时间序 列数据挖掘。 为此,在使用动态时间弯曲度量相似 性之前,通常先对时间序列数据进行数据降维,不仅 可以得到反映时间序列大部分信息的低维特征表 示,而且还能近似表示原始时间序列的整体性信息。 除此之外,在分类过程中,针对低频时间序列数据缺 少具体局部信息的状况,序列被归为哪一类通常可 能取决于其整体形状,而不是局限于严格的数值比 较。 因此,相似性度量的结果不仅需要充分考虑序 列的具体数值,也要考虑序列整体形态(凹凸性)。 传统研究方法是对时间序列进行数据降维,然 后使用传统距离公式直接进行相似性度量。 由于数 据降维会损耗时间序列的部分信息,实验效果也就 相当于以准确性来换取时间效率。 鉴于时间序列具 体数据值的重要性、形态的特殊性、度量准确性以及 高运行效率的必要性,结合分段聚合近似以及数值 导数,提出一种基于分段聚合近似和数值导数的动 态时间弯曲方法,称为分段聚合导数距离(piecewise approximation derivative distance, PADD)。 该方法 主要综合考虑时间序列的具体数值信息和形态特 征,以获得更好的度量效果,提高运行效率,减少异 常点对度量的影响为目标,同时从时间序列的整体 数据匹配和形态的凸凹性出发,更为完善地度量时 间序列异步相关性。 时间序列 S = (s1 ,s2 ,…,sn ) 和 Q = (q1 ,q2 ,…, qm ) ,通过分段聚合近似方法对它们进行数据降维 并进行整体数据的特征表示,即 S = PAA(S,ws) 和 Q = PAA(Q,wq) ,其中 ws 和 wq 为降维后维度,也是 分段数目。 另外,为了反映原始时间序列整体形态 的特征,利用数据导数来反映 PAA 对原始时间序列 降维后的序列进行整体形态特征描述。 利用式(4) 对 S - 和 Q - 进行数据导数计算,以反映原始时间序列 的整体形态特征,即 S′ 和 Q′ 。 最后,利用动态时间 弯曲方法分别对( S - , Q - )和( S′ , Q′ )进行距离度 量,并综合两者的加权平均作为新方法的距离度量 第 2 期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 ·251·

.252. 智能系统学报 第11卷 函数,即 的波动形态:3)实现均值特征序列的导数表示,以 DpADD(S,Q)=aDTW(S,Q)+BDTW(S',Q') 便更好地反映特征序列的形态变化情况。最后,利 (5) 用式(6)同时从均值特征序列和导数特征序列来反 式中:aB是通过 映原始时间序列的数据信息,以确保距离度量函数 (a cos20 能够较好地通过特征序列之间的数值关系来反映原 (6) (B=sin20' 0c[0.] 始时间序列之间的数值和形态变化关系。 求解得到。如图3所示,参数αB可以通过三角公 另外,从算法的整个描述过程,容易分析得到新 方法的计算时间效率。长度为n的时间序列进行分 式求解得到,两者取值范围均在[0,1],且式(6)确 保了两者之和为1,使其特征序列的动态时间弯曲 段聚合近似时,其时间复杂度为O(n),计算一阶导 距离是线性组合关系。为方便起见,系数αB可由 数的时间复杂度也为O(n)。另外,对PAA特征序 参数0来确定。 列和导数序列进行DTW距离度量所需要的时间复 杂度分别为0(w,0,)和0((0,-2)(0,-2),故 PADD整个算法过程的时间复杂度近似为 sin0 0(210,0。+4n)。由于分段数目心,和0,通常远小 于原始时间序列的长度,即心,≤n和W,≤n,故 PADD的时间复杂度O(2w,",+4n)要低于与传统 0 DTW和DDTW的时间复杂度O(n2)。特别地,数 值实验的分类结果和时间计算效率分析表明, cos PADD能够较好地度量时间序列的相似性,反映数 图3参数aB选取原理 Fig.3 The principle of selecting parameters a and B 据形态之间的变化关系,进而提高时间序列数据挖 掘算法的分类结果,还能在低维特征空间下获得较 结合上述思想,本文提出的分段聚合导数距离 高的时间效率。 (PADD)算法步骤如下: 输入时间序列S=(s1,52,…,5n)和Q=(91, 3数值实验 92,…,9m),分段数目心,和心,以及参数日: 为了更好地理解和检验PADD方法的性能,实 输出度量距离DPADD(S,Q)。 验通过对时间序列数据集进行分类实验,与传统 1)分别对时间序列进行平均分段,每个子序列 DTW和DDTW方法进行比较,验证新方法在不同时 长度分别为k,=n/w,和k。=m/0,。 间序列数据集中的距离度量质量和时间计算效率。 2)根据PAA思想,对每个子序列进行均值表 3.1分类实验 示,获得PAA序列S=(s1,52,…,5,)和Q=(91, 实验一共进行两个阶段,1)训练模型,使用“留 2,…,4,),其中两组特征序列的元素分别为5:= 一法”(leave-one-out)求出合适的参数0构建度量距 离:2)测试模型,得到分类效果。由于时间序列取 。1 和9,石之 值范围差距较大,度量相似性结果可能会出现很大 j) 4° 偏差,因此有必要对所有时间序列数据进行归一化 3)利用式(4)分别对PAA序列进行数据导数 处理,消除量纲。 求解,得到基于导数的特征序列S”=(s'1,s'2,…, 使用训练集训练模型过程中,给定时间序列分 s'-2)和Q'=(q'1,9'2,…,9'4-2)。 段数目w以及范围为[0,π/2]且步长为0.01的0, 4)利用DTW分别对上述两种特征序列进行度 利用分段聚合近似以及一阶求导分别得到新的特征 量距离,并实现线性组合,即DPADD(S,Q)= 序列。训练阶段结合“枚举法”测试在地情况下每 aDTW(S,Q)+BDTW(S',Q') 个0的分类情况,选择错误率最小的0作为该心情 在上述算法中,1)实现了时间序列的分段,使 况下的最优参数。一旦求得参数立即构建度量距离 用等划分的方法实现数据划分并获得相应的子序列 公式(5),进入2)利用最近邻(1-NN)分类方法检测 片段:2)中方法对子序列段的均值特征表示,而且 该距离公式分类效果。 大量研究结果表明[9],对于高维时间序列来说, 图4给出了数据集ECG在不同w取值下的最 PAA方法可以保留足够的数据信息来反映原序列 佳参数0。根据式(5)与式(6)易知,9取值越大
函数,即 DPADD(S,Q) = αDTW(S,Q) + βDTW(S′,Q′) (5) 式中: α、β 是通过 α = cos 2 θ β = sin 2 θ { , θ ⊂ [0, π 2 ] (6) 求解得到。 如图 3 所示,参数 α、β 可以通过三角公 式求解得到,两者取值范围均在[0,1],且式(6)确 保了两者之和为 1,使其特征序列的动态时间弯曲 距离是线性组合关系。 为方便起见,系数 α、β 可由 参数 θ 来确定。 图 3 参数 α、β 选取原理 Fig.3 The principle of selecting parameters α and β 结合上述思想,本文提出的分段聚合导数距离 (PADD)算法步骤如下: 输入 时间序列 S = (s1 ,s2 ,…,sn ) 和 Q = (q1 , q2 ,…,qm ) ,分段数目 ws 和 wq 以及参数 θ ; 输出 度量距离 DPADD(S,Q) 。 1)分别对时间序列进行平均分段,每个子序列 长度分别为 ks = n / ws 和 kq = m / wq 。 2)根据 PAA 思想,对每个子序列进行均值表 示,获得 PAA 序列 S = ( s - 1 ,s - 2 ,…,s - ws ) 和 Q = ( q - 1 , q - 2 ,…,q - wq ) ,其中两组特征序列的元素分别为 s - i = 1 ks ∑ iks j = ks (i-1) +1 sj 和 q - i = 1 kq ∑ ikq j = ks (i-1) +1 qj 。 3)利用式(4) 分别对 PAA 序列进行数据导数 求解,得到基于导数的特征序列 S′ = (s′1 ,s′2 ,…, s′ws -2 ) 和 Q′ = (q′1 ,q′2 ,…,q′wq -2 ) 。 4)利用 DTW 分别对上述两种特征序列进行度 量 距 离, 并 实 现 线 性 组 合, 即 DPADD(S,Q) = αDTW(S,Q) + βDTW(S′,Q′) 。 在上述算法中,1) 实现了时间序列的分段,使 用等划分的方法实现数据划分并获得相应的子序列 片段;2)中方法对子序列段的均值特征表示,而且 大量研究结果表明[19] ,对于高维时间序列来说, PAA 方法可以保留足够的数据信息来反映原序列 的波动形态;3) 实现均值特征序列的导数表示,以 便更好地反映特征序列的形态变化情况。 最后,利 用式(6)同时从均值特征序列和导数特征序列来反 映原始时间序列的数据信息,以确保距离度量函数 能够较好地通过特征序列之间的数值关系来反映原 始时间序列之间的数值和形态变化关系。 另外,从算法的整个描述过程,容易分析得到新 方法的计算时间效率。 长度为 n 的时间序列进行分 段聚合近似时,其时间复杂度为 O(n) ,计算一阶导 数的时间复杂度也为 O(n) 。 另外,对 PAA 特征序 列和导数序列进行 DTW 距离度量所需要的时间复 杂度分别为 O(wswq) 和 O((ws - 2)(wq - 2)) ,故 PADD 整 个 算 法 过 程 的 时 间 复 杂 度 近 似 为 O(2wswq +4n) 。 由于分段数目 ws 和 wq 通常远小 于原始时间序列的长度,即 ws ≪ n 和 wq ≪ n ,故 PADD 的时间复杂度 O(2wswq + 4n) 要低于与传统 DTW 和 DDTW 的时间复杂度 O(n 2 ) 。 特别地,数 值实验 的 分 类 结 果 和 时 间 计 算 效 率 分 析 表 明, PADD 能够较好地度量时间序列的相似性,反映数 据形态之间的变化关系,进而提高时间序列数据挖 掘算法的分类结果,还能在低维特征空间下获得较 高的时间效率。 3 数值实验 为了更好地理解和检验 PADD 方法的性能,实 验通过对时间序列数据集进行分类实验,与传统 DTW 和 DDTW 方法进行比较,验证新方法在不同时 间序列数据集中的距离度量质量和时间计算效率。 3.1 分类实验 实验一共进行两个阶段,1)训练模型,使用“留 一法”(leave⁃one⁃out)求出合适的参数 θ 构建度量距 离;2)测试模型,得到分类效果。 由于时间序列取 值范围差距较大,度量相似性结果可能会出现很大 偏差,因此有必要对所有时间序列数据进行归一化 处理,消除量纲。 使用训练集训练模型过程中,给定时间序列分 段数目 w 以及范围为 [0,π/ 2] 且步长为 0.01 的 θ, 利用分段聚合近似以及一阶求导分别得到新的特征 序列。 训练阶段结合“枚举法”测试在 w 情况下每 个 θ 的分类情况,选择错误率最小的 θ 作为该 w 情 况下的最优参数。 一旦求得参数立即构建度量距离 公式(5),进入 2)利用最近邻(1⁃NN)分类方法检测 该距离公式分类效果。 图 4 给出了数据集 ECG 在不同 w 取值下的最 佳参数 θ 。 根据式(5)与式(6)易知, θ 取值越大, ·252· 智 能 系 统 学 报 第 11 卷
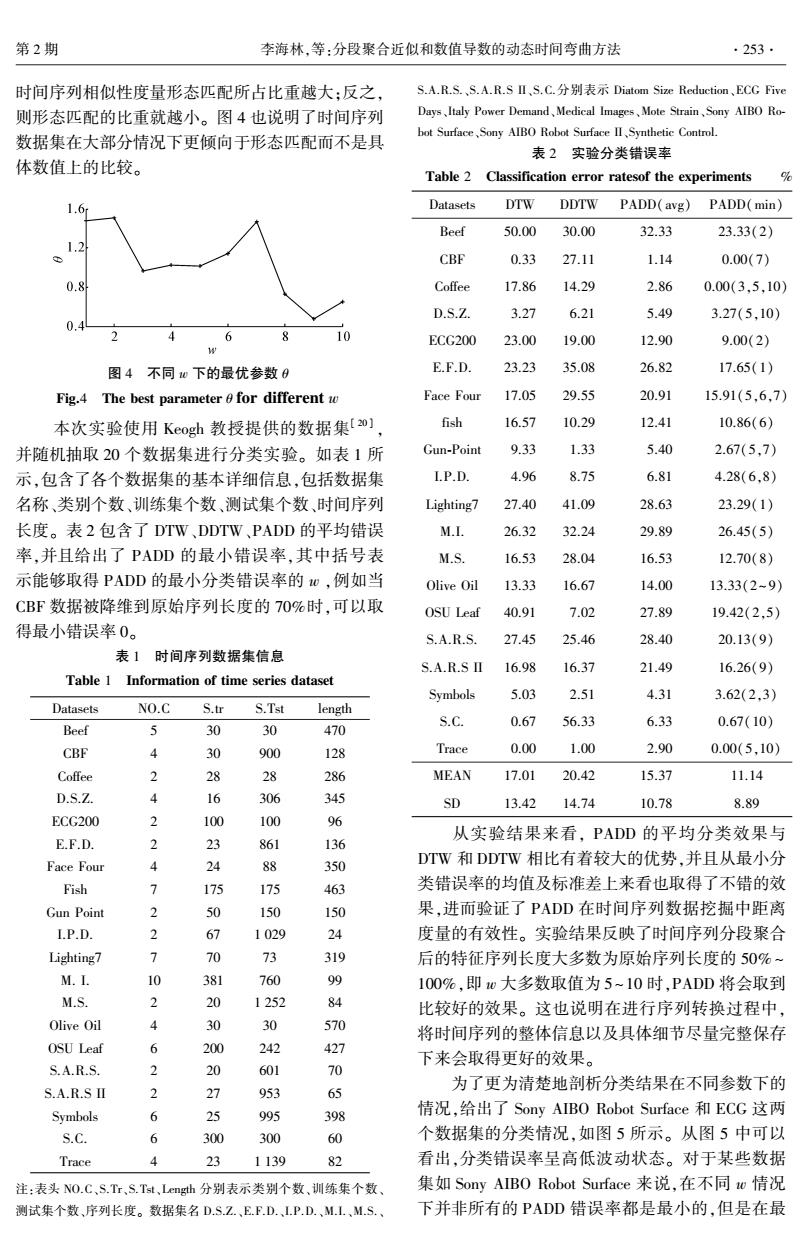
第2期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 .253. 时间序列相似性度量形态匹配所占比重越大:反之 S.A.R.S.、S.A.R.SⅡ、S.C.分别表示Diatom Size Reduction、ECG Five 则形态匹配的比重就越小。图4也说明了时间序列 Days、Italy Power Demand、Medical Images、Mote Strain,Sony AIBO Ro-- bot Surface,Sony AlBO Robot Surface II,Synthetic Control. 数据集在大部分情况下更倾向于形态匹配而不是具 表2实验分类错误率 体数值上的比较。 Table 2 Classification error ratesof the experiments Datasets DTW DDTW PADD(avg) PADD(min) Beef 50.00 30.00 32.33 23.33(2) CBF 0.33 27.11 1.14 0.00(7) Coffee 17.86 14.29 2.86 0.00(3,5,10) D.S.Z. 3.27 6.21 5.49 3.27(5.10) 6 10 ECG200 23.00 19.00 12.90 9.00(2) 图4不同w下的最优参数0 E.F.D. 23.23 35.08 26.82 17.65(1) Fig.4 The best parameter for different w Face Four 17.05 29.55 20.91 15.91(5,6,7) 本次实验使用Keogh教授提供的数据集[0] fish 16.57 10.29 12.41 10.86(6) 并随机抽取20个数据集进行分类实验。如表1所 Gun-Point 9.33 1.33 5.40 2.67(5,7) 示,包含了各个数据集的基本详细信息,包括数据集 I.P.D. 4.96 8.75 6.81 4.28(6,8) 名称、类别个数、训练集个数、测试集个数、时间序列 Lighting7 27.40 41.09 28.63 23.29(1) 长度。表2包含了DTW、DDTW、PADD的平均错误 M.I. 26.32 32.24 29.89 26.45(5) 率,并且给出了PADD的最小错误率,其中括号表 M.S. 16.53 28.04 16.53 12.70(8) 示能够取得PADD的最小分类错误率的w,例如当 Olive Oil 13.33 16.67 14.00 13.33(2-9) CBF数据被降维到原始序列长度的70%时,可以取 OSU Leaf 40.91 7.02 27.89 19.42(2,5) 得最小错误率0。 S.A.R.S. 27.45 25.46 28.40 20.13(9) 表1时间序列数据集信息 S.A.R.SΠ 16.98 16.37 21.49 16.26(9) Table 1 Information of time series dataset Symbols 5.03 2.51 4.31 3.62(2,3) Datasets NO.C S.tr S.Tst length 5 S.C. 0.67 56.33 6.33 0.67(10) Beef 30 30 470 CBF 4 30 900 128 Trace 0.00 1.00 2.90 0.00(5,10) Coffee 2 28 28 286 MEAN 17.01 20.42 15.37 11.14 D.S.Z. 4 16 306 345 SD 13.42 14.74 10.78 8.89 ECG200 2 100 100 96 从实验结果来看,PADD的平均分类效果与 E.F.D. 2 23 861 136 Face Four 4 24 88 350 DTW和DDTW相比有着较大的优势,并且从最小分 Fish 7 175 175 463 类错误率的均值及标准差上来看也取得了不错的效 Gun Point 2 150 150 果,进而验证了PADD在时间序列数据挖掘中距离 I.P.D. 2 67 1029 24 度量的有效性。实验结果反映了时间序列分段聚合 Lighting7 7 70 13 319 后的特征序列长度大多数为原始序列长度的50%~ M.I. 10 381 760 99 100%,即0大多数取值为5~10时,PADD将会取到 M.S. 2 20 1252 84 比较好的效果。这也说明在进行序列转换过程中, Olive Oil 4 30 30 570 将时间序列的整体信息以及具体细节尽量完整保存 OSU Leaf 6 200 242 427 下来会取得更好的效果。 S.A.R.S. 2 20 601 70 S.A.R.SΠ 2 27 为了更为清楚地剖析分类结果在不同参数下的 953 65 Symbols 情况,给出了Sony AIBO Robot Surface和ECG这两 6 3 995 398 S.C. 6 300 300 60 个数据集的分类情况,如图5所示。从图5中可以 Trace 23 1139 82 看出,分类错误率呈高低波动状态。对于某些数据 注:表头NO.C、S.Tr,S.Tst、Length分别表示类别个数、训练集个数 集如Sony AIB0 Robot Surface来说,在不同w情况 测试集个数、序列长度。数据集名D.S.Z.、EFD.、LP.D.、ML.、M.S.、 下并非所有的PADD错误率都是最小的,但是在最
时间序列相似性度量形态匹配所占比重越大;反之, 则形态匹配的比重就越小。 图 4 也说明了时间序列 数据集在大部分情况下更倾向于形态匹配而不是具 体数值上的比较。 图 4 不同 w 下的最优参数 θ Fig.4 The best parameter θ for different w 本次实验使用 Keogh 教授提供的数据集[ 20 ] , 并随机抽取 20 个数据集进行分类实验。 如表 1 所 示,包含了各个数据集的基本详细信息,包括数据集 名称、类别个数、训练集个数、测试集个数、时间序列 长度。 表 2 包含了 DTW、DDTW、PADD 的平均错误 率,并且给出了 PADD 的最小错误率,其中括号表 示能够取得 PADD 的最小分类错误率的 w ,例如当 CBF 数据被降维到原始序列长度的 70%时,可以取 得最小错误率 0。 表 1 时间序列数据集信息 Table 1 Information of time series dataset Datasets NO.C S.tr S.Tst length Beef 5 30 30 470 CBF 4 30 900 128 Coffee 2 28 28 286 D.S.Z. 4 16 306 345 ECG200 2 100 100 96 E.F.D. 2 23 861 136 Face Four 4 24 88 350 Fish 7 175 175 463 Gun Point 2 50 150 150 I.P.D. 2 67 1 029 24 Lighting7 7 70 73 319 M. I. 10 381 760 99 M.S. 2 20 1 252 84 Olive Oil 4 30 30 570 OSU Leaf 6 200 242 427 S.A.R.S. 2 20 601 70 S.A.R.S II 2 27 953 65 Symbols 6 25 995 398 S.C. 6 300 300 60 Trace 4 23 1 139 82 注:表头 NO.C、S.Tr、S.Tst、Length 分别表示类别个数、训练集个数、 测试集个数、序列长度。 数据集名 D.S.Z.、E.F.D.、I.P.D.、M.I.、M.S.、 S.A.R.S.、S.A.R.S II、S.C.分别表示 Diatom Size Reduction、ECG Five Days、Italy Power Demand、Medical Images、Mote Strain、Sony AIBO Ro⁃ bot Surface、Sony AIBO Robot Surface II、Synthetic Control. 表 2 实验分类错误率 Table 2 Classification error ratesof the experiments % Datasets DTW DDTW PADD(avg) PADD(min) Beef 50.00 30.00 32.33 23.33(2) CBF 0.33 27.11 1.14 0.00(7) Coffee 17.86 14.29 2.86 0.00(3,5,10) D.S.Z. 3.27 6.21 5.49 3.27(5,10) ECG200 23.00 19.00 12.90 9.00(2) E.F.D. 23.23 35.08 26.82 17.65(1) Face Four 17.05 29.55 20.91 15.91(5,6,7) fish 16.57 10.29 12.41 10.86(6) Gun⁃Point 9.33 1.33 5.40 2.67(5,7) I.P.D. 4.96 8.75 6.81 4.28(6,8) Lighting7 27.40 41.09 28.63 23.29(1) M.I. 26.32 32.24 29.89 26.45(5) M.S. 16.53 28.04 16.53 12.70(8) Olive Oil 13.33 16.67 14.00 13.33(2~ 9) OSU Leaf 40.91 7.02 27.89 19.42(2,5) S.A.R.S. 27.45 25.46 28.40 20.13(9) S.A.R.S II 16.98 16.37 21.49 16.26(9) Symbols 5.03 2.51 4.31 3.62(2,3) S.C. 0.67 56.33 6.33 0.67(10) Trace 0.00 1.00 2.90 0.00(5,10) MEAN 17.01 20.42 15.37 11.14 SD 13.42 14.74 10.78 8.89 从实验结果来看, PADD 的平均分类效果与 DTW 和 DDTW 相比有着较大的优势,并且从最小分 类错误率的均值及标准差上来看也取得了不错的效 果,进而验证了 PADD 在时间序列数据挖掘中距离 度量的有效性。 实验结果反映了时间序列分段聚合 后的特征序列长度大多数为原始序列长度的 50% ~ 100%,即 w 大多数取值为 5~10 时,PADD 将会取到 比较好的效果。 这也说明在进行序列转换过程中, 将时间序列的整体信息以及具体细节尽量完整保存 下来会取得更好的效果。 为了更为清楚地剖析分类结果在不同参数下的 情况,给出了 Sony AIBO Robot Surface 和 ECG 这两 个数据集的分类情况,如图 5 所示。 从图 5 中可以 看出,分类错误率呈高低波动状态。 对于某些数据 集如 Sony AIBO Robot Surface 来说,在不同 w 情况 下并非所有的 PADD 错误率都是最小的,但是在最 第 2 期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 ·253·

·254. 智能系统学报 第11卷 小错误率上却能够优于DTW和DDTW的错误率。 290.5 90.5 然而,在有些数据集如ECG,不管0取何值,新方法 0.4 解0.4 飞 的分类错误率都是低于另外两者的错误率。 =0.3 誓0.3 罕 0.35-PADD-DTW 0.25 0.2 DDTW --PADD-DTW S01 0.1 03 0.20 aavd DDTW 0 0.1 0.20.30.40.5 0 0.10.20.30.40.5 张 DTW错误率I% DDTW错误率/% 0.25 彩 (a)PADD平均错误率vs (b)PADD平均错误率vs 0.10 DTW错误率 DDTW错误率 0.5 0.5t 0.20 0.05 246 810 6 8 10 卧0.4 解0.4 (a)Sony AlBO RobotSurface (b)ECG 0.3 点 +++ 把0.3 + 图5分类错误率和时间序列分段聚合长度的关系 Fig.5 The relationship of classification and the length 0.1 十 of time series piecewise aggregation 0 0.10.20.30.40.5 0 0.10.20.30.40.5 从图5中发现,不同数据集呈现出来的性能不 DTW错误率/% DDTW错误率/% 一样。由于分段聚合近似采用的是均值作为替代 (c)PADD最小错误率vs (d)PADD最小错误率vs DTW错误率 DDTW错误率 值,这并非最佳的降维方法,因此,若数据集中的序 图7分类错误率的比较 列数据波动较多、振幅较大,会对降维效果造成一定 Fig.7 Comparison of classification error rates 的影响。如图6所示。 图7中子图(a)、(b)分别描述PADD的平均错 误率与DTW、DDTW的错误率比较,子图(c)、(d) 分别描述PADD最小错误率与DTW、DDTW错误率 比较。结果分析表明,不管从平均错误率还是最小 错误率角度来比较,PADD错误率所对应的坐标纵 10203040506070 轴值相对较小,使其偏向于DTW和DDTW所代表 时间戳/s (a)Sony AIBO Robot Surface 的横轴值较大,大多散点都偏向于DTW和DDTW, 故说明PADD具有较小的分类错误率,进行验证了 本文新方法在时间序列度量中的有效性和优越性。 3.2时间效率分析 本实验使用“留一法”(leave-one-out)求解参 20 4060 80 100 数,参数确定后立即构建度量距离公式。特征序列 时间戰/s 长度越长,计算所要消耗的时间越大,且成数量级增 (b)ECG 图6实验数据集序列示例 长。如图8所示,描述了数据集Sony AIB0 Robot Fig.6 The example of datasets Surface和ECG在不同o条件下PADD时间效率与 图6分别给出的是训练集Sony AIBO Robot DTW、DDTW的时间效率比较。 Surface和ECG的3条时间序列,可以观察到子图 由于DDTW需要利用式(4)预先对时间序列数 (a)的序列在整体波动上比子图(b)的多。因此, 据进行求导,因此DDTW时间效率略高于DTW时 影响了序列降维的效果,给后续的相似性度量造成 间效率。另外,随着特征序列长度0的增长,PADD 了一定的影响。由于数据集的特性会给本方法造成 消耗的时间也随之增长。当分段数目增长到 一定的影响,因此,本方法适合波动较为平缓的数据 定程度时,PADD的计算时间消耗会大于传统DTW 集,并会取得较好的效果。 和DDTW方法。理论上结合时间复杂度的分析可 图7描述的是PADD的平均分类错误率以及最 知,PADD的时间复杂度近似为O(202+4n),DTW 小分类错误率与DTW、DDTW的错误率的比较,为 和DDTW的时间复杂度为O(n2),当且仅当0< 了便于直观比较,数值均经过归一化后取值范围为 (n-2)2-4 时,PADD的时间效率要低于DTW [0,0.5],数值偏向方表示对应方法的错误率较大
小错误率上却能够优于 DTW 和 DDTW 的错误率。 然而,在有些数据集如 ECG,不管 w 取何值,新方法 的分类错误率都是低于另外两者的错误率。 图 5 分类错误率和时间序列分段聚合长度的关系 Fig.5 The relationship of classification and the length of time series piecewise aggregation 从图 5 中发现,不同数据集呈现出来的性能不 一样。 由于分段聚合近似采用的是均值作为替代 值,这并非最佳的降维方法,因此,若数据集中的序 列数据波动较多、振幅较大,会对降维效果造成一定 的影响。 如图 6 所示。 图 6 实验数据集序列示例 Fig.6 The example of datasets 图 6 分别给出的是训练集 Sony AIBO Robot Surface 和 ECG 的 3 条时间序列,可以观察到子图 (a) 的序列在整体波动上比子图( b)的多。 因此, 影响了序列降维的效果,给后续的相似性度量造成 了一定的影响。 由于数据集的特性会给本方法造成 一定的影响,因此,本方法适合波动较为平缓的数据 集,并会取得较好的效果。 图 7 描述的是 PADD 的平均分类错误率以及最 小分类错误率与 DTW、DDTW 的错误率的比较,为 了便于直观比较,数值均经过归一化后取值范围为 [0,0.5],数值偏向方表示对应方法的错误率较大。 图 7 分类错误率的比较 Fig.7 Comparison of classification error rates 图 7 中子图(a)、(b)分别描述 PADD 的平均错 误率与 DTW、DDTW 的错误率比较,子图( c)、( d) 分别描述 PADD 最小错误率与 DTW、DDTW 错误率 比较。 结果分析表明,不管从平均错误率还是最小 错误率角度来比较,PADD 错误率所对应的坐标纵 轴值相对较小,使其偏向于 DTW 和 DDTW 所代表 的横轴值较大,大多散点都偏向于 DTW 和 DDTW, 故说明 PADD 具有较小的分类错误率,进行验证了 本文新方法在时间序列度量中的有效性和优越性。 3.2 时间效率分析 本实验使用“留一法” ( leave⁃one⁃out) 求解参 数,参数确定后立即构建度量距离公式。 特征序列 长度越长,计算所要消耗的时间越大,且成数量级增 长。 如图 8 所示,描述了数据集 Sony AIBO Robot Surface 和 ECG 在不同 w 条件下 PADD 时间效率与 DTW、DDTW 的时间效率比较。 由于 DDTW 需要利用式(4)预先对时间序列数 据进行求导,因此 DDTW 时间效率略高于 DTW 时 间效率。 另外,随着特征序列长度 w 的增长,PADD 消耗的时间也随之增长。 当分段数目 w 增长到一 定程度时,PADD 的计算时间消耗会大于传统 DTW 和 DDTW 方法。 理论上结合时间复杂度的分析可 知,PADD 的时间复杂度近似为 O(2w 2 + 4n) ,DTW 和 DDTW 的时间复杂度为 O(n 2 ) ,当且仅当 w < (n - 2) 2 - 4 2 时,PADD 的时间效率要低于 DTW ·254· 智 能 系 统 学 报 第 11 卷

第2期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 ·255. 和 DDTW。因此,在分段比例超过约 2268-2275. /(n-2)2-4 /n= 一2时,时间效率便开始降 [2]MARSZA EK A,BURCZY SKI T.Modeling and forecasting n financial time series with ordered fuzzy candlesticks[J].In- formation sciences,2014,273:144-155. 低。可以发现,n为任意值,该比例均约为70%,从 [3]ZAMORA M,LAMBERT A,MONTERO G.Effect of some 图中也清楚地看到,DTW、DDTW、PADD三者在分 meteorological phenomena on the wind potential of Baja Cal- 段比例约为70%的地方相交。另外,在PADD过程 ifornia[].Energy procedia,2014,57:1327-1336. 中会涉及到一些辅助计算,故若大于某一特定降维 [4]GRAVIO G D,MANCINI M,PATRIARCA R,et al.Over- 之后的维度时,PADD将会消耗更多的计算时间。 all safety performance of air traffic management system: 然而,如图8所示,在数据降维后的低维空间中, forecasting and monitoring[J].Safety science,2015,72: PADD可以取得较好的时间效率,具有一定的计算 351-362. 性能优势。 [5]李海林,郭韧万校基.基于特征矩阵的多元时间序列最 0.08 小距离度量方法[J].智能系统学报,2015,10(3):442- 0.04 447. 0.03 m0.06 LI Hailin,GUO Ren,WAN Xiaoji.A minimum distance 这0.02 蒸0.04 measurement method for multivariate time series based on the feature matrix[J.CAAI transactions on intelligent sys- 0.01 0.02 tems,2015,10(3):442-447. [6]SAKOE H,CHIBA S.Dynamic programming algorithm opti- 2 4 6 810 4 6 8 10 mization for spoken word recognition[J].IEEE transactions (a)Sony AIBO Robot Surface (b)ECG on acoustics,speech,and signal processing,1978,26 图83种方法的时间效率 (1):43-49. Fig.8 Time efficiency of the three methods [7]IZAKIAN H,PEDRYCZ W,JAMAL I.Fuzzy clustering of time series data using dynamic time warping distance[J. 4 结束语 Engineering applications of artificial intelligence,2015,39: 235-244. 针对动态弯曲方法对时间序列数据相似性 [8 ]ZHANG Zheng,TANG Ping,DUAN Rubing.Dynamic time 度量质量和效率的局限性,以及从简化模型的角 warping under pointwise shape context[J].Information sci- 度考虑,本文提出一种基于分段聚合近似和数值 ences,.2015,315:88-101. 导数的动态时间弯曲方法,结合分段聚合近似算 [9]李正欣,张凤鸣,李克武.基于DTW的多元时间序列模 法以及数值求导将时间序列进行转换,得到符合 式匹配方法[J].模式识别与人工智能,2011,24(3): 要求的特征序列,构建新的距离公式对新的特征 425-430. 序列进行相似性度量。数值实验结果表明,与传 LI Zhengxin,ZHANG Fengming,LI Kewu.DTW based pat- 统的动态时间弯曲度量方法相比,在分类效果和 tern matching method for multivariate time series[J].Pat- 计算性能上具有一定的优势。通过实验发现,针 tern recognition and artificial intelligence,2011,24(3): 425-430. 对波动较为平缓的数据进行挖掘,将会取得更好的 效果。特别地,在数据压缩量较大的低维空间下,新 [10]LI Hailin.Asynchronism-based principal component analy- sis for time series data mining[J].Expert systems with ap- 方法在保证分类质量的前提下,能够获得较好的时 plications,2014,41(6):2842-2850. 间效率。另外,参数选择是一个至关重要的步骤,不 [11]KEOGH E,PAZZANI M J.Derivative dynamic time war- 同参数对实验结果具有一定的影响,将来需要对参 ping[C]//Proceedings of the 1st SIAM International Con- 数选择做进一步探讨和研究。 ference on Data Mining.Chicago,IL,USA,2001:1-11. 参考文献: [12]JEONG Y S,JAYARAMAN R.Support vector-based algo- rithms with weighted dynamic time warping kernel function [1]韩敏,许美玲,王新迎.多元时间序列的子空间回声状 for time series classification [J].Knowledge-based sys- 态网络预测模型[J].计算机学报,2014,37(11):2268- tems,2015,75:184-191. 2275. [13]GORECKI T,LUCZAK M.Using derivatives in time series HAN Min,XU Meiling,WANG Xinying.A multivariate classification[].Data mining and knowledge discovery, time series prediction model based on subspace echo state 2013,26(2):310-331. network[J].Chinese journal of computers,2014,37(11): [14]李海林,杨丽彬.时间序列数据降维和特征表示方法
和 DDTW。 因 此, 在 分 段 比 例 超 过 约 (n - 2) 2 - 4 2 / n = n - 2 n 时,时间效率便开始降 低。 可以发现, n 为任意值,该比例均约为 70%,从 图中也清楚地看到,DTW、DDTW、PADD 三者在分 段比例约为 70%的地方相交。 另外,在 PADD 过程 中会涉及到一些辅助计算,故若大于某一特定降维 之后的维度时,PADD 将会消耗更多的计算时间。 然而,如图 8 所示,在数据降维后的低维空间中, PADD 可以取得较好的时间效率,具有一定的计算 性能优势。 图 8 3 种方法的时间效率 Fig.8 Time efficiency of the three methods 4 结束语 针对动态弯曲方法对时间序列数据相似性 度量质量和效率的局限性,以及从简化模型的角 度考虑,本文提出一种基于分段聚合近似和数值 导数的动态时间弯曲方法,结合分段聚合近似算 法以及数值求导将时间序列进行转换,得到符合 要求的特征序列,构建新的距离公式对新的特征 序列进行相似性度量。 数值实验结果表明,与传 统的动态时间弯曲度量方法相比,在分类效果和 计算性能上具有一定的优势。 通过实验发现,针 对波动较为平缓的数据进行挖掘,将会取得更好的 效果。 特别地,在数据压缩量较大的低维空间下,新 方法在保证分类质量的前提下,能够获得较好的时 间效率。 另外,参数选择是一个至关重要的步骤,不 同参数对实验结果具有一定的影响,将来需要对参 数选择做进一步探讨和研究。 参考文献: [1]韩敏, 许美玲, 王新迎. 多元时间序列的子空间回声状 态网络预测模型[J]. 计算机学报, 2014, 37(11): 2268⁃ 2275. HAN Min, XU Meiling, WANG Xinying. A multivariate time series prediction model based on subspace echo state network[J]. Chinese journal of computers, 2014, 37(11): 2268⁃2275. [2]MARSZA EK A, BURCZY SKI T. Modeling and forecasting financial time series with ordered fuzzy candlesticks[J]. In⁃ formation sciences, 2014, 273: 144⁃155. [3]ZAMORA M, LAMBERT A, MONTERO G. Effect of some meteorological phenomena on the wind potential of Baja Cal⁃ ifornia[J]. Energy procedia, 2014, 57: 1327⁃1336. [4]GRAVIO G D, MANCINI M, PATRIARCA R, et al. Over⁃ all safety performance of air traffic management system: forecasting and monitoring[ J]. Safety science, 2015, 72: 351⁃362. [5]李海林, 郭韧 万校基. 基于特征矩阵的多元时间序列最 小距离度量方法[J]. 智能系统学报, 2015, 10(3): 442⁃ 447. LI Hailin, GUO Ren, WAN Xiaoji. A minimum distance measurement method for multivariate time series based on the feature matrix[J]. CAAI transactions on intelligent sys⁃ tems, 2015, 10(3): 442⁃447. [6]SAKOE H, CHIBA S. Dynamic programming algorithm opti⁃ mization for spoken word recognition[J]. IEEE transactions on acoustics, speech, and signal processing, 1978, 26 (1): 43⁃49. [7]IZAKIAN H, PEDRYCZ W, JAMAL I. Fuzzy clustering of time series data using dynamic time warping distance [ J]. Engineering applications of artificial intelligence, 2015, 39: 235⁃244. [8]ZHANG Zheng, TANG Ping, DUAN Rubing. Dynamic time warping under pointwise shape context[ J]. Information sci⁃ ences, 2015, 315: 88⁃101. [9]李正欣, 张凤鸣, 李克武. 基于 DTW 的多元时间序列模 式匹配方法[ J]. 模式识别与人工智能, 2011, 24( 3): 425⁃430. LI Zhengxin, ZHANG Fengming, LI Kewu. DTW based pat⁃ tern matching method for multivariate time series[ J]. Pat⁃ tern recognition and artificial intelligence, 2011, 24 ( 3): 425⁃430. [10]LI Hailin. Asynchronism⁃based principal component analy⁃ sis for time series data mining[J]. Expert systems with ap⁃ plications, 2014, 41(6): 2842⁃2850. [11]KEOGH E, PAZZANI M J. Derivative dynamic time war⁃ ping[C] / / Proceedings of the 1st SIAM International Con⁃ ference on Data Mining. Chicago, IL, USA, 2001: 1⁃11. [12]JEONG Y S, JAYARAMAN R. Support vector⁃based algo⁃ rithms with weighted dynamic time warping kernel function for time series classification [ J ]. Knowledge⁃based sys⁃ tems, 2015, 75: 184⁃191. [13]GÓRECKI T, ŁUCZAK M. Using derivatives in time series classification[ J]. Data mining and knowledge discovery, 2013, 26(2): 310⁃331. [14]李海林, 杨丽彬. 时间序列数据降维和特征表示方法 第 2 期 李海林,等:分段聚合近似和数值导数的动态时间弯曲方法 ·255·

.256· 智能系统学报 第11卷 [J].控制与决策,2013,28(11):1718-1722. [19]LIN J,KEOGH E,WEI Li,et al.Experiencing SAX:a LI Hailin,YANG Libin.Method of dimensionality reduc- novel symbolic representation of time series[J].Data min- tion and feature representation for time series[J].Control ing and knowledge discovery,2008,15(2):107-144. and decision,.2013,28(11):1718-1722. [20]KEOGH E,XI X,WEI L,et al.The UCR time series [15]BANKO Z,ABONYI J.Mixed dissimilarity measure for classification/clustering homepage EB/OL].2007.ht- piecewise linear approximation based time series applica- tp://www.cs.ucr.edu/~eamonn/time_series_data/. tions[J].Expert systems with applications,2015,42 作者简介: (21):7664-7675. 李海林.男,1982年生,副教授,博 [16]AGRAWAL R,FALOUTSOS C,SWAMI A.Efficient sim- 士,主要研究方向为数据挖掘与决策支 ilarity search in sequence databases[C]//Proceedings of 持,主持国家自然科学基金、省部级基 the 4th International Conference on Foundations of Data 金多项,发表学术论文30余篇,其中被 Organization and Algorithms.Berlin Heidelberg:Springer, SCI检索11篇,EI检索10余篇。 1993.730:69-84. [17]WANG Hongfa.Clustering of hydrological time series based on discrete wavelet transform[J].Physics procedia,2012, 25:1966-1972. 梁叶,女,1992年生,硕士研究生, [18]WENG Xiaoqing,SHEN Junyi.Classification of multivari- 主要研究方向为数据挖掘与金融数据 ate time series using two-dimensional singular value decom- 分析。 position[J].Knowledge-based systems,2008,21(7): 535-539. 2016年第11届EEE国际应用计算智能和信息研讨会 2016 IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI) Authors are welcome to submit original and unpublished papers and attend the IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI 2016)to be held on May 12-14,2016 in Timisoara,Romania. TOPICS include but not limited to Computational Intelligence Intelligent Mechatronics Systems Engineering Intelligent Manufacturing Systems Intelligent Control Intelligent Robotics Informatics Website:http://conf.uni-obuda.hu/saci2016/
[J]. 控制与决策, 2013, 28(11): 1718⁃1722. LI Hailin, YANG Libin. Method of dimensionality reduc⁃ tion and feature representation for time series[ J]. Control and decision, 2013, 28(11): 1718⁃1722. [15] BANKÓ Z, ABONYI J. Mixed dissimilarity measure for piecewise linear approximation based time series applica⁃ tions [ J ]. Expert systems with applications, 2015, 42 (21): 7664⁃7675. [16]AGRAWAL R, FALOUTSOS C, SWAMI A. Efficient sim⁃ ilarity search in sequence databases [ C] / / Proceedings of the 4th International Conference on Foundations of Data Organization and Algorithms. Berlin Heidelberg: Springer, 1993, 730: 69⁃84. [ 17]WANG Hongfa. Clustering of hydrological time series based on discrete wavelet transform[J]. Physics procedia, 2012, 25: 1966⁃1972. [18]WENG Xiaoqing, SHEN Junyi. Classification of multivari⁃ ate time series using two⁃dimensional singular value decom⁃ position[ J]. Knowledge⁃based systems, 2008, 21 ( 7): 535⁃539. [19]LIN J, KEOGH E, WEI Li, et al. Experiencing SAX: a novel symbolic representation of time series[J]. Data min⁃ ing and knowledge discovery, 2008, 15(2): 107⁃144. [20]KEOGH E, XI X, WEI L, et al. The UCR time series classification / clustering homepage [ EB/ OL ]. 2007. ht⁃ tp: / / www.cs.ucr.edu / ~ eamonn / time_series_data / . 作者简介: 李海林,男,1982 年生,副教授,博 士,主要研究方向为数据挖掘与决策支 持,主持国家自然科学基金、省部级基 金多项,发表学术论文 30 余篇,其中被 SCI 检索 11 篇,EI 检索 10 余篇。 梁叶,女,1992 年生,硕士研究生, 主要研究方向为数据挖掘与金融数据 分析。 2016 年第 11 届 IEEE 国际应用计算智能和信息研讨会 2016 IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI) Authors are welcome to submit original and unpublished papers and attend the IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI 2016) to be held on May 12-14, 2016 in Timisoara, Romania. TOPICS include but not limited to Computational Intelligence Intelligent Mechatronics Systems Engineering Intelligent Manufacturing Systems Intelligent Control Intelligent Robotics Informatics Website: http: / / conf.uni⁃obuda.hu / saci2016 / ·256· 智 能 系 统 学 报 第 11 卷