
第11卷第1期 智能系统学报 Vol.11 No.1 2016年2月 CAAI Transactions on Intelligent Systems Feh.2016 D0I:10.11992/is.201505024 网络出版地址:htp://www.cmki.net/kcms/detail/23.1538.TP.20151229.0837.016.html 基于最小最大概率机的迁移学习分类算法 王晓初2,包芳23,王士同1,许小龙1 (1.江南大学数字媒体学院,江苏无锡214122:2.江阴职业技术学院江苏省信息融合软件工程技术研发中心,江苏 江阴214405:3.江阴职业技术学院计算机科学系,江苏江阴214405) 摘要:传统的迁移学习分类算法利用源域中大量有标签的数据和目标域中少量有标签的数据解决相关但不相同 目标域的数据分类问题,但对于已知源域的不同类别数据均值的迁移学习分类问题并不适用。为了解决这个问题, 利用源域的数据均值和目标域的少量标记数据构造迁移学习约束项,对最小最大概率机进行正则化约束,提出了基 于最小最大概率机的迁移学习分类算法,简称TL-MPM。在20 News Groups数据集上的实验结果表明,目标域数据 较少时,所提算法具有更高的分类正确率,从而说明了算法的有效性。 关键词:迁移学习:最小最大概率机:分类:源域:目标域:正则化 中图分类号:TP391.4文献标志码:A文章编号:1673-4785(2016)01-0084-09 中文引用格式:王晓初,包芳,王士同,等.基于最小最大概率机的迁移学习分类算法[J].智能系统学报,2016,11(1):84-92 英文引用格式:WANG Xiaochu,BAO Fang,WANG Shitong,etal.Transfer learning classification algorithms based on minimax probability machine[].CAAI Transactions on Intelligent Systems,2016,11(1):84-92. Transfer learning classification algorithms based on minimax probability machine WANG Xiaochu'.2,BAO Fang2.3,WANG Shitong',XU Xiaolong' (1.School of Digital Media,Jiangnan University,Wuxi 214122,China;2.Information Fusion Software Engineering Research and De- velopment Center of Jiangsu Province,Jiangyin Pdyteehnie College,Jiangyin 214405,China;3.Department of Computer Science, Jiangyin Pdyteehnie College,Jiangyin 214405,China) Abstract:Traditional transfer learning classification algorithms solve related but not identical)data classification issues by using a large number of labeled samples in the source domain and small amounts of labeled samples in the target domain.However,this technique does not apply to the transfer learning of data from different categories of learned source domain data.To solve this problem,we constructed a transfer learning constraint term using the source domain data and the limited labeled data in the target domain to generate a regularized constraint for the minimax probability machine.We propose a transfer learning classification algorithm based on the minimax probabil- ity machine known as TL-MPM.Experimental results on 20 Newsgroups data sets demonstrate that the proposed al- gorithm has higher classification accuracy for small amounts of target domain data.Therefore,we confirm the effec- tiveness of the proposed algorithm. Keywords:transfer learning;minimax probability machine;classification;source domain;target domain;regulari- zation 迁移学习是机器学习领域的一个新方向,是对 及对未来迁移学习潜在的问题。文献[2]推广了传 机器学习能力的一次拓展,具有很重要的研究价值。 统的AdaBoost算法,提出Tradaboosting迁移学习算 文献[1]讨论了迁移学习的应用,现阶段研究进展 法,该算法思想是利用boosting的技术来过滤掉辅 助数据中那些与源训练数据最不相像的数据。其中 收稿日期:2015-05-11.网络出版日期:2015-12-29. 基金项目:国家自然科学基金资助项目(61170122,61272210) boosting的作用是建立一种自动调整权重的机制,于 通信作者:王晓初.E-mail:icnice@ycah.net
第 11 卷第 1 期 智 能 系 统 学 报 Vol.11 №.1 2016 年 2 月 CAAI Transactions on Intelligent Systems Feb. 2016 DOI:10.11992 / tis.201505024 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20151229.0837.016.html 基于最小最大概率机的迁移学习分类算法 王晓初1,2 ,包芳2,3 ,王士同1 ,许小龙1 (1.江南大学 数字媒体学院,江苏 无锡 214122; 2. 江阴职业技术学院 江苏省信息融合软件工程技术研发中心,江苏 江阴 214405; 3.江阴职业技术学院 计算机科学系,江苏 江阴 214405) 摘 要:传统的迁移学习分类算法利用源域中大量有标签的数据和目标域中少量有标签的数据解决相关但不相同 目标域的数据分类问题,但对于已知源域的不同类别数据均值的迁移学习分类问题并不适用。 为了解决这个问题, 利用源域的数据均值和目标域的少量标记数据构造迁移学习约束项,对最小最大概率机进行正则化约束,提出了基 于最小最大概率机的迁移学习分类算法,简称 TL⁃MPM。 在 20 News Groups 数据集上的实验结果表明,目标域数据 较少时,所提算法具有更高的分类正确率,从而说明了算法的有效性。 关键词:迁移学习;最小最大概率机;分类;源域;目标域;正则化 中图分类号:TP391.4 文献标志码:A 文章编号:1673⁃4785(2016)01⁃0084⁃09 中文引用格式:王晓初,包芳,王士同,等.基于最小最大概率机的迁移学习分类算法[J]. 智能系统学报, 2016, 11(1): 84⁃92. 英文引用格式:WANG Xiaochu, BAO Fang, WANG Shitong, et al. Transfer learning classification algorithms based on minimax probability machine[J]. CAAI Transactions on Intelligent Systems, 2016, 11(1): 84⁃92. Transfer learning classification algorithms based on minimax probability machine WANG Xiaochu 1,2 , BAO Fang 2,3 , WANG Shitong 1 , XU Xiaolong 1 (1. School of Digital Media, Jiangnan University, Wuxi 214122, China; 2. Information Fusion Software Engineering Research and De⁃ velopment Center of Jiangsu Province, Jiangyin Pdyteehnie College, Jiangyin 214405, China; 3. Department of Computer Science, Jiangyin Pdyteehnie College, Jiangyin 214405, China) Abstract:Traditional transfer learning classification algorithms solve related (but not identical) data classification issues by using a large number of labeled samples in the source domain and small amounts of labeled samples in the target domain. However, this technique does not apply to the transfer learning of data from different categories of learned source domain data. To solve this problem, we constructed a transfer learning constraint term using the source domain data and the limited labeled data in the target domain to generate a regularized constraint for the minimax probability machine. We propose a transfer learning classification algorithm based on the minimax probabil⁃ ity machine known as TL⁃MPM. Experimental results on 20 Newsgroups data sets demonstrate that the proposed al⁃ gorithm has higher classification accuracy for small amounts of target domain data. Therefore, we confirm the effec⁃ tiveness of the proposed algorithm. Keywords:transfer learning; minimax probability machine; classification; source domain; target domain; regulari⁃ zation 收稿日期:2015⁃05⁃11. 网络出版日期:2015⁃12⁃29. 基金项目:国家自然科学基金资助项目(61170122, 61272210). 通信作者:王晓初. E⁃mail:icnice@ yeah.net. 迁移学习是机器学习领域的一个新方向,是对 机器学习能力的一次拓展,具有很重要的研究价值。 文献[1]讨论了迁移学习的应用,现阶段研究进展 及对未来迁移学习潜在的问题。 文献[2]推广了传 统的 AdaBoost 算法,提出 Tradaboosting 迁移学习算 法,该算法思想是利用 boosting 的技术来过滤掉辅 助数据中那些与源训练数据最不相像的数据。 其中 boosting 的作用是建立一种自动调整权重的机制,于

第1期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·85. 是重要的辅助训练数据的权重将会增加,不重要的 解为a。,对应k取得最小值k。,此时(2)式中的不 辅助训练数据的权重将会减小。调整权重之后,这 等号变为等号,可得 些带权重的辅助训练数据将会作为额外的训练数 b.=ax-k√Ja.a.=aly-k√a.E,a. 据,与源训练数据一起来提高分类模型的可靠度。 (4) 文献[3]通过维数约简的思想,设法学习出一个低 对于测试样本x",若axe-b,≥0则x为 维隐特征空间,使得源域的数据和目标域的数据在 正样本;反之x"为负样本。 该空间的分布相同或接近对方。文献[4-7]将协同 1.2非线性部分 学习、正则化、模糊理论等用于迁移学习,取得了很 好的效果。文献[8]同样提出了基于正则化的迁移 样本映射到非线性:x→p(x)~((x),Σs) 学习模型,文献[9]提出了图协同正则化的迁移学 y→(y)~(p(y),)),这里:R4→R",核函数 习。文献[10]将迁移学习的思想用于广告显示。 可写为K(x:,x)=P(x:)T(x)。核函数用于最小 前面对迁移学习的研究,大多是在源域的数据 最大概率机,决策超平面写为ap(z)-b=0,其中a, 样本具体标签已知的假设下进行的。本文针对源域 (z)∈R"。表达式(3)非线性形式为 中不同类别的数据均值和目标域中少量有标签的数 minv√aΣ,a+√aΣ,)a 据已知的分类问题,以最小最大概率机分类算法模 s.ta'(p(x)-p(y))=1 (5) 型为基础,提出TL-MPM算法,本算法最大的优点 如果a中有一分量正交于p(x:),i=1,2,…,N 是并不知道源域的数据训练样本的具体标签,仅知 和(y:),i=1,2,…,N,的子空间,N、V,分别为正 道均值信息,从而减小了对标记源域的数据所需花 负标记样本的个数,那么这个分量不会影响到目标 费的代价。 函数的结果,因此可以将a写成 1 最小最大概率机 a=∑a,e(x)+∑B.e(x) (6) 1.1线性部分 设Y=[a1a2…axB1B2…Bx,],[K]:=K(x, 假设x和y为2维分类问题的2个随机变量, 服从某种分布x~(x,三),y~(少,三,),这里x,y∈ )为核数,【医1.=∑(与,医,1. R,三,三,∈R,x,少,三,三,分别为随机变量x和 ∑产K,2)则约束条件可表示为 1 y的均值和方差。最小最大概率机实现分类的目的 就是找到一个超平面a'z-b=0,(a,z∈R,b∈ ao(x)-a"e(y)=yk,-yk,(7) R)四,将2类样本在样本估计的均值和方差的前 又假设1.m为m维全1列向量,且K.= 提下,按照最大概率分离,所以分类问题可以描述 K-1,同样形式飞,=K,-1x,其中i=1,2,…, 为 may a s.t..inf Pria'r≥b}≥a N时乙,=x,i=N+1,…,N+W,时z=yN,那么正 负样本的协方差表达式可表示为 inf Pra'y≤b}≥a (1) 式中:a为正确分类概率,inf表示下确界。主要是 a'Σma=i YKK 保证在错分概率最小的情况下,通过一个核函数将 特征映射到高维空间,并构造一个最优分类超平面, d'soky (8) 从而实现特征分类。(1)式可归结为一个带约束的 经过上面核化后,约束条件和协方差的表达式 优化问题2: 变为(7)式和(8)式的形式,带人α表示的非线性表 max k s.t.-b+aTx≥k√a∑a 达式(5)式可得y表示的非线性目标函数: k,a,6 b-a'y≥ka,a (2) min 下yKKy+ XKK 式中:k=√a/1-a)。化简式(2)并削去k且不 st.y(k.-k,)=1 (9) 失一般性地令a'(x-y)=1,最大化k等价于: 目标函数(9)也为凸优化问题。 min a'sa+√a∑,as.t.a'(x-y)=1(3) 显然,与线性部分算法一致。当Y取最优解 目标函数(3)为凸优化问题5),假设求得最优 Y,,对应k取得最小值k。,可得
是重要的辅助训练数据的权重将会增加,不重要的 辅助训练数据的权重将会减小。 调整权重之后,这 些带权重的辅助训练数据将会作为额外的训练数 据,与源训练数据一起来提高分类模型的可靠度。 文献[3]通过维数约简的思想,设法学习出一个低 维隐特征空间,使得源域的数据和目标域的数据在 该空间的分布相同或接近对方。 文献[4-7]将协同 学习、正则化、模糊理论等用于迁移学习,取得了很 好的效果。 文献[8]同样提出了基于正则化的迁移 学习模型,文献[9]提出了图协同正则化的迁移学 习。 文献[10]将迁移学习的思想用于广告显示。 前面对迁移学习的研究,大多是在源域的数据 样本具体标签已知的假设下进行的。 本文针对源域 中不同类别的数据均值和目标域中少量有标签的数 据已知的分类问题,以最小最大概率机分类算法模 型为基础,提出 TL⁃MPM 算法,本算法最大的优点 是并不知道源域的数据训练样本的具体标签,仅知 道均值信息,从而减小了对标记源域的数据所需花 费的代价。 1 最小最大概率机 1.1 线性部分 假设 x 和 y 为 2 维分类问题的 2 个随机变量 , 服从某种分布 x ~ (x - ,Σx),y ~ (y - ,Σy),这里x,y ∈ R d ,Σx,Σy ∈ R d×d , x - ,y - , Σx,Σy 分别为随机变量 x 和 y 的均值和方差。 最小最大概率机实现分类的目的 就是找到一个超平面 a T z - b = 0, ( a, z ∈ R d , b ∈ R) [11] ,将 2 类样本在样本估计的均值和方差的前 提下,按照最大概率分离 ,所以分类问题可以描述 为 max α,a,b α s.t. inf Pr{a T x ≥ b} ≥ α inf Pr{a T y ≤ b} ≥ α (1) 式中:α 为正确分类概率,inf 表示下确界。 主要是 保证在错分概率最小的情况下,通过一个核函数将 特征映射到高维空间,并构造一个最优分类超平面, 从而实现特征分类。 (1)式可归结为一个带约束的 优化问题[12⁃13] : max k,a,b k s.t. - b + a T x - ≥ k a T Σxa b - a T y - ≥ k a T Σya (2) 式中:k = α/ (1-α) [14] 。 化简式(2)并削去 k 且不 失一般性地令 a T (x - -y - )= 1,最大化 k 等价于: min a a T Σxa + a T Σya s.t. a T (x - - y - ) = 1 (3) 目标函数(3)为凸优化问题[15] ,假设求得最优 解为 a∗,对应 k 取得最小值 k∗,此时(2)式中的不 等号变为等号,可得 b∗ = a T ∗x - - k a T ∗Σxa∗ = a T ∗y - - k a T ∗Σya∗ (4) 对于测试样本 x new ,若 a T ∗ x new -b∗ ≥0 则 x new为 正样本;反之 x new为负样本。 1.2 非线性部分 样本映射到非线性:x aφ( x) ~ (φ( x),Σφ(x) ) y aφ(y) ~ (φ(y),Σφ(y) ),这里 φ:R d aR n ,核函数 可写为 K(xi,xj)= φ (xi) Tφ(xj)。 核函数用于最小 最大概率机,决策超平面写为 a Tφ(z)-b = 0,其中 a, φ(z)∈R n 。 表达式(3)非线性形式为 min a a T Σφ(x) a + a T Σφ(y) a s.t. a T (φ(x - ) - φ(y - )) = 1 (5) 如果 a 中有一分量正交于 φ(xi),i = 1,2,…,Nx 和 φ(yi),i = 1,2,…,Ny 的子空间,Nx、Ny 分别为正 负标记样本的个数,那么这个分量不会影响到目标 函数的结果,因此可以将 a 写成 a = ∑ Nx i = 1 αiφ(xi) + ∑ Ny i = 1 βiφ(xi) (6) 设 γ= [α1 α2… αΝx β1 β2… βΝy ],[Kx]i =K(xj, zi) 为核函数, [ k ~ x]i = 1 Nx ∑ Nx j = 1 K(xj,zi), [ k ~ y]i = 1 Ny ∑ Ny j = 1 K(yj,zi) 则约束条件可表示为 a Tφ(x) - a Tφ(y) = γ T k ~ x - γ T k ~ y (7) 又 假 设 1m 为 m 维 全 1 列 向 量, 且 K ~ x = Kx -1Nx k ~ T x ,同样形式 K ~ y = Ky -1Ny k ~ T y ,其中 i = 1,2,…, Nx 时 zi = xi,i = Nx +1,…,Nx +Ny 时 zi = yi-Nx ,那么正 负样本的协方差表达式可表示为 a T Σφ(x) a = 1 Nx γ TK ~ T x K ~ xγ a T Σφ(y) a = 1 Ny γ TK ~ T yK ~ yγ (8) 经过上面核化后,约束条件和协方差的表达式 变为(7)式和(8)式的形式,带入 a 表示的非线性表 达式(5)式可得 γ 表示的非线性目标函数: min γ 1 Nx γ TK ~ T xK ~ xγ + 1 Ny γ TK ~ T yK ~ yγ s.t. γ T ( k ~ x - k ~ y) = 1 (9) 目标函数(9)也为凸优化问题。 显然,与线性部分算法一致。 当 γ 取最优解 γ∗,对应 k 取得最小值 k∗,可得 第 1 期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·85·

·86 智能系统学报 第11卷 b.=y尾-k. ykky.= L=lf(E,))-f((x,)I2+ f(,)-f(y)‖2 (12) y.k,-k. KY. (10) TL-MPM算法的理论依据是:若两个领域相关, 源域的数据和目标域的数据在超平面所在空间的均 对于测试样本x",若a!p(x)-b。= 值应相近。通过在MPM线性目标式(3)中增加L, ∑[y.],K(z,x)≥0,则x为正样本;反之 非线性目标式(5)中增加入L实现两个域之间的迁移 xew为负样本。 学习。加入迁移学习项后的线性目标函数可以写为 2基于最小最大概率机的迁移学习分 min√a.a+√a,a+AL 类算法 s.t.a(x,-y,)=1 (13) 2.1TL-MPM算法的应用背景 非线性目标函数可写为 实际问题中,有时候当前分类目标的标记样本并 min√aΣeea+√aEe)a+ALt 不充分,这样对于分类结果的预测会带来很大偏差。 s.t.a'(p(a,)-p(y,)=1 (14) 而当前分类目标往往和上一阶段的分类目标比较,既 式中:L和L4表示两个域的差异程度,参数入控制 有新的变化,又具有某些类似的特性。比如超市不同 惩罚程度。本算法对入在103~103范围内进行交 季度的营业额、银行不同月份的贷款数、公司每个阶 叉验证选优。当入取值较小时,说明两个领域之间 段的出货量、港务每年吞吐量等,一般情况每个阶段 均值相关性较高;反之,两个领域之间均值相关性较 虽然有波动,不会有太大的偏差,但由于种种原因,上 小。TL-MPM算法的原理可用图1表示。 个阶段的样本信息,并不能完全得知:即使得知,也不 能直接将所有信息用在当前阶段中,因为上一阶段的 源域训练集正负 目标域训练集少量 均值往往是易于得知,并且各个阶段数据均值波动基 类样本均值 样本 本很小。所以上一阶段均值是对当前阶段极为有用 的信息。这样在当前阶段信息不充分的情况下可以 构造迁移学习项 充分利用上个阶段的均值信息进行迁移学习。 2.2TL-MPM算法的理论依据 构建最小最大概率机 在最小最大概率机训练的过程中,如式(3)所 描述的,通过最小化√a∑a和√a∑,a之和,使得 基于最小最大概率机的 样本在超平面所在空间分布为线性可分的形式,但 迁移学习算法 在样本很少的情况下,协方差和均值并不能很好地 图1TL-MPM算法 代表整体的协方差和均值,那么训练出来的a值实 Fig.1 Flowchart of TL-MPM 际上并不是最优的。对于相关但不相同的数据,源 为了更清晰地展示TL-MPM算法的作用原理及效 域的数据和目标域的数据具有相似性,所以均值波 果,在二维数据上做了线性算法的模拟实验。图2为 动性并不大,可以预测目标域的数据均值与源域的 源域样本分布,横轴x表示样本的一维,纵轴y表示样 数据均值或多或少是相近的,所以在训练过程中,可 本的二维,图中“×”表示目标域正样本,“+”号表示目 以利用源域的数据均值和目标域的数据均值实现数 标域负样本,菱形和正方形分别表示已知的目标域正 据迁移学习。在具体的实现中,是通过最小化源域 样本和负样本,实心圆表示目标域正样本和负样本均 的数据均值和目标域的数据均值在超平面所在空间 值,空心圆表示源域正样本和负样本均值。虚线为目 的欧氏距离来实现的。假设源域的数据正负类样本 标域少量标记样本在MPM算法下得到的分类超平面, 的均值分别为x,和y,目标域少量数据的样本的均 实线为TL-MPM算法下得到的分类超平面。 值分别为x,和y,可得超平面所在空间的均值之间 由图3可以明显看出,源域正负样本的均值和 的线性距离可以表示为 目标域样本的均值相差并不是很大。正是由于这种 L=‖fx,)-fx)I2+lfy,)-fy)‖2 源域样本与目标域样本的相关性,经过源域的数据 均值与目标域的数据均值的迁移学习,得到的目标 (11) 域的分类超平面更为准确。 均值之间的非线性距离表示为
b∗ = γ T ∗ k ~ x - k∗ 1 Nx γ T ∗K ~ T x K ~ xγ∗ = γ T ∗ k ~ y - k∗ 1 Ny γ T ∗K ~ T yK ~ yγ∗ (10) 对 于 测 试 样 本 x new , 若 a T ∗ φ ( x new ) - b∗ = ∑Nx +Ny i [γ∗]iK(zi,x new ) ≥0,则 x new 为正样本;反之 x new为负样本。 2 基于最小最大概率机的迁移学习分 类算法 2.1 TL⁃MPM 算法的应用背景 实际问题中,有时候当前分类目标的标记样本并 不充分,这样对于分类结果的预测会带来很大偏差。 而当前分类目标往往和上一阶段的分类目标比较,既 有新的变化,又具有某些类似的特性。 比如超市不同 季度的营业额、银行不同月份的贷款数、公司每个阶 段的出货量、港务每年吞吐量等,一般情况每个阶段 虽然有波动,不会有太大的偏差,但由于种种原因,上 个阶段的样本信息,并不能完全得知;即使得知,也不 能直接将所有信息用在当前阶段中,因为上一阶段的 均值往往是易于得知,并且各个阶段数据均值波动基 本很小。 所以上一阶段均值是对当前阶段极为有用 的信息。 这样在当前阶段信息不充分的情况下可以 充分利用上个阶段的均值信息进行迁移学习。 2.2 TL⁃MPM 算法的理论依据 在最小最大概率机训练的过程中,如式(3) 所 描述的,通过最小化 a T Σxa 和 a T Σya 之和,使得 样本在超平面所在空间分布为线性可分的形式,但 在样本很少的情况下,协方差和均值并不能很好地 代表整体的协方差和均值,那么训练出来的 a 值实 际上并不是最优的。 对于相关但不相同的数据,源 域的数据和目标域的数据具有相似性,所以均值波 动性并不大,可以预测目标域的数据均值与源域的 数据均值或多或少是相近的,所以在训练过程中,可 以利用源域的数据均值和目标域的数据均值实现数 据迁移学习。 在具体的实现中,是通过最小化源域 的数据均值和目标域的数据均值在超平面所在空间 的欧氏距离来实现的。 假设源域的数据正负类样本 的均值分别为x - s 和y - s,目标域少量数据的样本的均 值分别为x - t 和y - t,可得超平面所在空间的均值之间 的线性距离可以表示为 L = ‖f(x - t) - f(x - s)‖2 + ‖f(y - t) - f(y - s)‖2 (11) 均值之间的非线性距离表示为 Lk = ‖f(φ(x - t)) - f(φ(x - s))‖2 + ‖f(φ(y - t)) - f(φ(y - s))‖2 (12) TL⁃MPM 算法的理论依据是:若两个领域相关, 源域的数据和目标域的数据在超平面所在空间的均 值应相近。 通过在 MPM 线性目标式(3)中增加 λL, 非线性目标式(5)中增加 λLk 实现两个域之间的迁移 学习。 加入迁移学习项后的线性目标函数可以写为 min a a T Σxa + a T Σya + λL s.t. a T (x - t - y - t) = 1 (13) 非线性目标函数可写为 min a a T Σφ(x) a + a T Σφ(y) a + λLk s.t. a T (φ(a - t) - φ(y - t)) = 1 (14) 式中:L 和 Lk 表示两个域的差异程度,参数 λ 控制 惩罚程度。 本算法对 λ 在10 -3 ~ 10 3 范围内进行交 叉验证选优。 当 λ 取值较小时,说明两个领域之间 均值相关性较高;反之,两个领域之间均值相关性较 小。 TL⁃MPM 算法的原理可用图 1 表示。 图 1 TL⁃MPM 算法 Fig.1 Flowchart of TL⁃MPM 为了更清晰地展示 TL⁃MPM 算法的作用原理及效 果,在二维数据上做了线性算法的模拟实验。 图 2 为 源域样本分布,横轴 x 表示样本的一维,纵轴 y 表示样 本的二维,图中“×”表示目标域正样本,“+”号表示目 标域负样本,菱形和正方形分别表示已知的目标域正 样本和负样本,实心圆表示目标域正样本和负样本均 值,空心圆表示源域正样本和负样本均值。 虚线为目 标域少量标记样本在 MPM 算法下得到的分类超平面, 实线为 TL⁃MPM 算法下得到的分类超平面。 由图 3 可以明显看出,源域正负样本的均值和 目标域样本的均值相差并不是很大。 正是由于这种 源域样本与目标域样本的相关性,经过源域的数据 均值与目标域的数据均值的迁移学习,得到的目标 域的分类超平面更为准确。 ·86· 智 能 系 统 学 报 第 11 卷
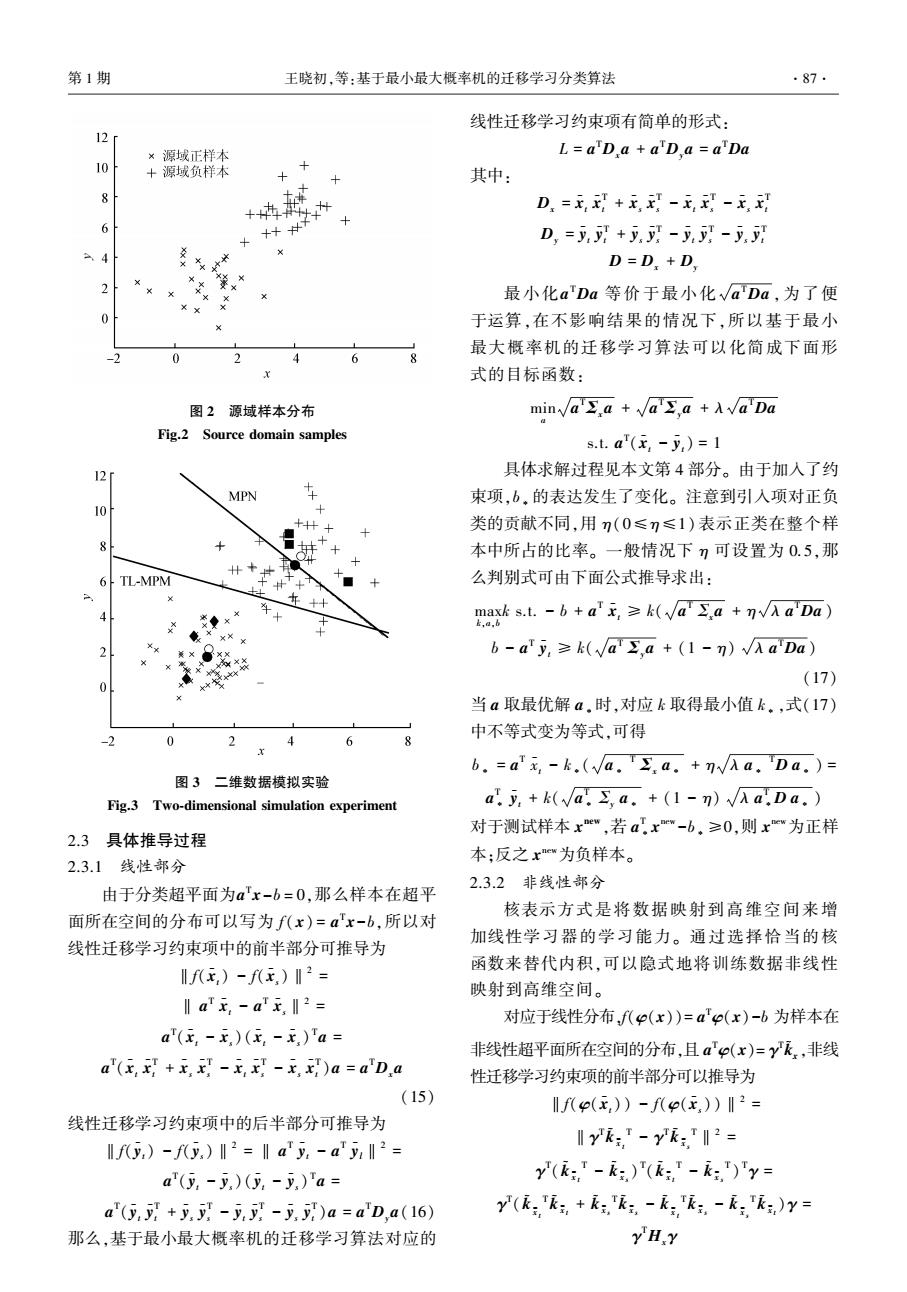
第1期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·87 线性迁移学习约束项有简单的形式: 12r ×源域正样本 L=aD a aD a=aDa 10 +源域负样本 其中: D=玉+无,-x,-E, 6 D,=y,+--少 D=D,+D. 2 最小化a'Da等价于最小化√aDa,为了便 Xx 0 于运算,在不影响结果的情况下,所以基于最小 最大概率机的迁移学习算法可以化简成下面形 6 式的目标函数: 图2源域样本分布 min√a.a+√a∑,a+A√aDa Fig.2 Source domain samples s.t.a'(-)=1 12 具体求解过程见本文第4部分。由于加人了约 MPN 束项,b,的表达发生了变化。注意到引入项对正负 10 + X 类的贡献不同,用n(0≤)≤1)表示正类在整个样 8 本中所占的比率。一般情况下7可设置为0.5,那 6 TL-MPM + 么判别式可由下面公式推导求出: 年+十 mas.t.-6+a'无,≥k(Vaa+AaDa) b-aTy,≥k(√Ja,a+(1-n)√AaDa) X (17) 当a取最优解a.时,对应k取得最小值k。,式(17) 中不等式变为等式,可得 0 2 4 6 x b.=a元,-k.(a..a.+n√Aa.Da.)= 图3二维数据模拟实验 Fig.3 Two-dimensional simulation experiment a.y,+k(va.s a.+(1-n)a.Da. 对于测试样本xe",若ax"-b.≥0,则xw为正样 2.3具体推导过程 2.3.1线性部分 本:反之xw为负样本。 2.3.2非线性部分 由于分类超平面为a'x-b=0,那么样本在超平 核表示方式是将数据映射到高维空间来增 面所在空间的分布可以写为f(x)=a'x-b,所以对 加线性学习器的学习能力。通过选择恰当的核 线性迁移学习约束项中的前半部分可推导为 函数来替代内积,可以隐式地将训练数据非线性 f(x,)-fx,)I2= 映射到高维空间。 ‖ax,-ax,I2= 对应于线性分布f(p(x))=a'e(x)-b为样本在 a'(x,-x,)(,-x)Ta= 非线性超平面所在空间的分布,且a'(x)=y飞,非线 a"(xx+x-xx-x)a=a'Da 性迁移学习约束项的前半部分可以推导为 (15) f八p(x,)-f(E)I2= 线性迁移学习约束项中的后半部分可推导为 lfy,)-fy,)‖2=lay,-ay‖2= yk:-yk= a(y,-y)(y-y,)'a= y(,-,)(k-:,)'y= a(5+y-y-y)a=a'D,a(16) y(飞,+飞,-无,生,-,飞,)y= 那么,基于最小最大概率机的迁移学习算法对应的 YHY
图 2 源域样本分布 Fig.2 Source domain samples 图 3 二维数据模拟实验 Fig.3 Two⁃dimensional simulation experiment 2.3 具体推导过程 2.3.1 线性部分 由于分类超平面为a T x-b = 0,那么样本在超平 面所在空间的分布可以写为 f( x) = a T x-b,所以对 线性迁移学习约束项中的前半部分可推导为 ‖f(x - t) - f(x - s)‖2 = ‖ a T x - t - a T x - s‖2 = a T (x - t - x - s)(x - t - x - s) T a = a T (x - t x - T t + x - s x - T s - x - t x - T s - x - s x - T t )a = a TDxa (15) 线性迁移学习约束项中的后半部分可推导为 ‖f(y - t) - f(y - s)‖2 = ‖ a T y - t - a T y - l‖2 = a T (y - t - y - s)(y - t - y - s) T a = a T (y - t y - T t + y - s y - T s - y - t y - T s - y - s y - T t )a = a TDya(16) 那么,基于最小最大概率机的迁移学习算法对应的 线性迁移学习约束项有简单的形式: L = a TDxa + a TDya = a TDa 其中: Dx = x - t x - T t + x - s x - T s - x - t x - T s - x - s x - T t Dy = y - t y - T t + y - s y - T s - y - t y - T s - y - s y - T t D = Dx + Dy 最小化a TDa 等价于最小化 a TDa ,为了便 于运算,在不影响结果的情况下,所以基于最小 最大概率机的迁移学习算法可以化简成下面形 式的目标函数: min a a T Σxa + a T Σya + λ a TDa s.t. a T (x - t - y - t) = 1 具体求解过程见本文第 4 部分。 由于加入了约 束项,b∗ 的表达发生了变化。 注意到引入项对正负 类的贡献不同,用 η(0≤η≤1) 表示正类在整个样 本中所占的比率。 一般情况下 η 可设置为 0.5,那 么判别式可由下面公式推导求出: max k,a,b k s.t. - b + a T x - t ≥ k( a T Σxa + η λ a TDa ) b - a T y - t ≥ k( a T Σya + (1 - η) λ a TDa ) (17) 当 a 取最优解 a∗时,对应 k 取得最小值 k∗,式(17) 中不等式变为等式,可得 b∗ = a T x - t - k∗( a∗ T Σx a∗ + η λ a∗ TD a∗ ) = a T ∗ y - t + k( a T ∗ Σy a∗ + (1 - η) λ a T ∗D a∗ ) 对于测试样本 x new ,若 a T ∗ x new -b∗ ≥0,则 x new为正样 本;反之 x new为负样本。 2.3.2 非线性部分 核表示方式是将数据映射到高维空间来增 加线性学习器的学习能力。 通过选择恰当的核 函数来替代内积,可以隐式地将训练数据非线性 映射到高维空间。 对应于线性分布,f(φ(x))= a Tφ(x)-b 为样本在 非线性超平面所在空间的分布,且 a Tφ(x)= γ T k ~ x ,非线 性迁移学习约束项的前半部分可以推导为 ‖f(φ(x - t)) - f(φ(x - s))‖2 = ‖γ T k ~ x - t T - γ T k ~ x - s T‖2 = γ T ( k ~ x - t T - k ~ x - s ) T ( k ~ x - t T - k ~ x - s T ) Tγ = γ T ( k ~ x - t T k ~ x - t + k ~ x - s T k ~ x - s - k ~ x - t T k ~ x - s - k ~ x - s T k ~ x - t )γ = γ THxγ 第 1 期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·87·

·88 智能系统学报 第11卷 非线性迁移学习约束项的后半部分可推导为 lfp(y))-f(p(,)‖2= 职A+月I三(a:+P,)++ yk-yk= 司Iya+m,)++ID(a,+F,)I店 Ek ykk(= (18) y(正,飞,+飞飞,-,-尼,)y= 3)令a=(x-y,)/‖x-y,‖2,B。=1,6。=1, YHY E。=1并带入(18)得到最小二乘问题,求解得vo: 那么,基于最小最大概率机的迁移学习算法对 4)k=1; 应的迁移学习线性约束项有简单的形式: 5)a:=a-1+Fy-,B=√a-2a4-,δ= L=YH Y +yH Y=YHY A√a-2,a-1,e=√a-Da-1并带入(18)式求解得 其中: Va: H=尼,呢,+尼生呢三,尼,尼生,-尼生呢 6)k=k+1: H=k+k-,k,-:呢 7)重复步骤5、6直到收敛或满足停止条件; H=H+ 8)最后求得:a.=a4,k.=1/(B+δ+e4),,b,= 最小化yHy等价于最小化√yHy,为了便于 ax-k.(B+me)。 运算,在不影响结果的情况下,基于最小最大概率机 4 实验结果与分析 的迁移学习算法可以化简成下面形式的目标函数: 为了验证TL-MPM算法的有效性,在常用的真 √Y'y+ 1 min √衣y+A分 1 实数据集:20 News Groups数据集上进行实验。20 News Groups数据集的信息如表I所示。 st.y(k,-k,)=1 表120 News Groups数据集 显然非线性目标函数求解方法与线性一致。当 Table 1 20 News Groups Data Y取最优解Y.时,对应k取得最小值k。,求取b,推 大类 小类 样本个数 理与线性部分类似,得到b.的表达式为 comp.graphics 997 b.=无-6.(发&7+A9a) comp.windows.x 998 comp comp.os.mswindows.misc 992 +.(P元y+1-AF comp.sys.ibm.pc.hardware 997 对于测试样本x,若:a.Tp(x)-b。= comp.sys.mac.hardware 996 ∑[y.]K(2x)≥0,则x为正样本;反 rec.motorcycles 997 rec.autos 998 之x为负样本。 rec rec.sport.baseball 998 3 TL-MPM算法解法流程 rec.sport.hockey 998 talk.politics.mideast 1000 线性部分和非线性部分目标函数形式相同, talk.politics.misc 998 都是非线性有约束优化问题,并且是凸优化问 talk 题。有好多方法可以选择[1618】,比如拟牛顿法, talk.politics.guns 1000 Rosen梯度投影法等,这里我们用递归最小二乘 talk.religion.misc 999 法对修正优化问题进行求解,下面只解析线性目 sci.crypt 998 标函数求解过程。 sci.med 998 sci 1)令a=a。+Fv,F的列正交于x,-y,: sci.space 999 2)式(16)可写为 sci.electronics 999
非线性迁移学习约束项的后半部分可推导为 ‖f(φ(y - )) - f(φ(y - l))‖2 = ‖γ T k ~ y - t T - γ T k ~ y - s T‖2 = γ T ( k ~ y - t T - k ~ y - s T )( k ~ y - t T - k ~ y - s T ) Tγ = γ T ( k ~ y - t T k ~ y - t + k ~ y - s T k ~ y - s - k ~ y - t T k ~ y - s - k ~ y - s T k ~ y - t )γ = γ THyγ 那么,基于最小最大概率机的迁移学习算法对 应的迁移学习线性约束项有简单的形式: Lk = γ THxγ + γ THyγ = γ THγ 其中: Hx = k ~ x - t T k ~ x - t + k ~ x - s T k ~ x - s - k ~ x - t T k ~ x - s - k ~ x - s T k ~ x - t Hy = k ~ y - t T k ~ y - t + k ~ y - s T k ~ y - s - k ~ y - t T k ~ y - s - k ~ y - s T k ~ y - t H = Hx + Hy 最小化 γ THγ 等价于最小化 γ THγ,为了便于 运算,在不影响结果的情况下,基于最小最大概率机 的迁移学习算法可以化简成下面形式的目标函数: min γ 1 Nx γ TK ~ T xK ~ xγ + 1 Ny γ TK ~ T yK ~ yγ + λ γ THγ s.t. γ T ( k ~ xt - k ~ ys ) = 1 显然非线性目标函数求解方法与线性一致。 当 γ 取最优解 γ∗时,对应 k 取得最小值 k∗,求取 b∗推 理与线性部分类似,得到 b∗的表达式为 b∗ = γ T ∗ k ~ xt - k∗( γ T 1 Nx K ~ x T K ~ xγ + ηλ γ THkγ) = γ T ∗ k ~ yt + k∗( γ T 1 Ny K ~ T y K ~ yγ + (1 - η)λ γ THkγ) 对于测试样本 x new , 若: a∗ Tφ(x new ) - b∗ = ∑ Nl +Nu i [γ∗] i K(zi,x new ) ≥ 0,则 x new 为正样本;反 之 x new 为负样本。 3 TL⁃MPM 算法解法流程 线性部分和非线性部分目标函数形式相同, 都是非线性有约束优化问题,并且 是 凸 优 化 问 题。 有好多方法可以选择[ 16⁃18] ,比如拟牛顿法, Rosen 梯度投影法等,这里我们用递归最小二乘 法对修正优化问题进行求解,下面只解析线性目 标函数求解过程。 1)令 a = a0 +Fv,F 的列正交于 x - t -y - t; 2)式(16)可写为 min β,δ,ε,v βk + 1 βk ‖ Σx 1/ 2 (ak + Fvk)‖2 2 + δk + 1 δk ‖Σ 1/ 2 y (ak + Fvk)‖2 2 + εk + λ εk ‖D 1/ 2 (ak + Fvk)‖2 2 (18) 3) 令 a0 = ( x - t - y - t ) / ‖x - t -y - t‖2 2 , β0 = 1, δ0 = 1, ε0 = 1并带入(18)得到最小二乘问题,求解得 v0 ; 4)k = 1; 5 ) ak = ak-1 + Fvk-1 , βk = a T k-1Σxak-1 , δk = λ a T k-1Σyak-1 ,εk = a T k-1Dak-1 并带入(18)式求解得 vk; 6)k = k+1; 7)重复步骤 5、6 直到收敛或满足停止条件; 8)最后求得:a∗ = ak,k∗ = 1 / (βk +δk +εk), b∗ = a T ∗x - -k∗(βk +ηεk)。 4 实验结果与分析 为了验证 TL⁃MPM 算法的有效性,在常用的真 实数据集:20 News Groups 数据集上进行实验。 20 News Groups 数据集的信息如表 1 所示。 表 1 20 News Groups 数据集 Table 1 20 News Groups Data 大类 小类 样本个数 comp comp.graphics 997 comp.windows.x 998 comp.os.mswindows.misc 992 comp.sys.ibm.pc.hardware 997 comp.sys.mac.hardware 996 rec rec.motorcycles 997 rec.autos 998 rec.sport.baseball 998 rec.sport.hockey 998 talk talk.politics.mideast 1 000 talk.politics.misc 998 talk.politics.guns 1 000 talk.religion.misc 999 sci sci.crypt 998 sci.med 998 sci.space 999 sci.electronics 999 ·88· 智 能 系 统 学 报 第 11 卷

第1期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·89· 为了方便实验的描述,对实验中涉及的有关符 MPM算法中的核函数都选取高斯核函数,参数σ在 号给出相应的定义,如表2所示。 (0.001,0.01,0.1,1,10,100,1000)中选取。TL-MPM 表2实验中涉及的符号定义 算法中的参数在(0.001,0.01,0.1,1,10,100,1000)中 Table 2 Definition of symbols in the experiment 选取。对表3处理好的6个真实分类数据集分别随 符号 定义 机独立重复10次实验,选取最优参数下的取值,表4、 Ds 源域数据集 表5和表6分别记录了10次独立重复实验正确率的 Dt 目标域数据集 均值。 仅利用目标域少量数据训练得到的目标域 表4目标域样本的1%训练结果 T-LMPM MPM线性分类器 Table 4 Results of 1%training samples in the target domain/% 仅利用目标域少量数据训练得到的目标域 数据集 T-LMPM T-KMPM LTL-MPM KTL-MPM T-KMPM MPM非线性分类器 comp ys rec 71.71 72.96 72.56 78.42 LTL-MPM 本文提出的TL-MPM算法得到的线性分类器 comp vs sci 66.46 74.16 72.22 76.49 KTL-MPM 本文提出的L,MPM算法得到的非线性分类器 comp ys talk 90.96 99.15 99.48 99.75 rec vs talk 60.51 71.29 66.26 76.14 4.1 20 News Groups数据集预处理 首先对数据集分成源域训练数据和目标域训练 rec vs sci 62.49 71.00 64.17 76.48 数据,具体的处理结果如表3所示。 sci vs talk 68.21 77.24 67.98 76.44 表320 News Groups数据集处理结果 Table 3 Results of 20News Groups Data set processing 表5目标域样本的5%训练结果 Datasets Ds Dt Table 5 Results of 5%training samples in the target domain/% comp.graphics comp.windows.x 数据集 T-LMPM T-KMPM LTL-MPM KTL-MPM comp vs rec rec.motorcycles rec.autos comp.sys.ibm.pc. comp ys rec 61.46 80.92 64.19 83.94 comp.os.mswindows.misc comp vs sci hardware comp ys sci 58.72 76.33 63.29 79.56 sci.crypt sci.med comp.os.mswindows comp vs talk 94.13 99.41 97.74 99.83 comp.sys.mac.hardware comp vs talk misc rec vs talk 57.36 76.30 60.80 78.60 talk.politics.mideast talk.politics.guns rec vs sci 57.12 78.81 57.49 81.50 rec.autos rec.sport.baseball rec vs talk talk.politics.misc talk.religion.misc sci vs talk 57.42 86.34 63.98 86.75 rec.autos rec.sport.hockey rec vs sci sci.space sci.electronics 表6目标域样本的10%训练结果 sci.med sci.space Table 6 Results of 10%training samples in the target domain/ sci vs talk talk.religion.misc talk.politics.mideast 数据集 T-LMPM T-KMPM LTL-MPM KTL-MPM 其次,由于20 News Groups文本数据集的特 comp vs rec 76.46 85.51 80.05 86.06 征数很大,为了实验的方便,用主元分析法对数 comp vs sci 70.87 84.75 75.00 83.70 据集的特征做降维预处理,取前100维构成新 的实验数据。 comp vs talk 96.16 99.32 98.66 99.69 4.2少量目标域训练样本上的实验结果与分析 rec vs talk 65.30 81.64 66.74 81.56 实验中取源域中的全部数据,分别取目标 rec vs sci 64.93 84.89 70.17 85.90 域中的1%、5%、10%的数据训练TL-MPM算法 sci vs talk 70.49 90.18 72.17 89.09 分类器和MPM算法分类器。在T-MPM和TL-
为了方便实验的描述,对实验中涉及的有关符 号给出相应的定义,如表 2 所示。 表 2 实验中涉及的符号定义 Table 2 Definition of symbols in the experiment 符号 定义 Ds 源域数据集 Dt 目标域数据集 T⁃LMPM 仅利用目标域少量数据训练得到的目标域 MPM 线性分类器 T⁃KMPM 仅利用目标域少量数据训练得到的目标域 MPM 非线性分类器 LTL⁃MPM 本文提出的 TL⁃MPM 算法得到的线性分类器 KTL⁃MPM 本文提出的 TL⁃MPM 算法得到的非线性分类器 4.1 20News Groups 数据集预处理 首先对数据集分成源域训练数据和目标域训练 数据,具体的处理结果如表 3 所示。 表 3 20News Groups 数据集处理结果 Table 3 Results of 20News Groups Data set processing Datasets Ds Dt comp vs rec comp.graphics rec.motorcycles comp.windows.x rec.autos comp vs sci comp.os.mswindows.misc sci.crypt comp. sys. ibm. pc. hardware sci.med comp vs talk comp.sys.mac.hardware talk.politics.mideast comp. os. mswindows. misc talk.politics.guns rec vs talk rec.autos talk.politics.misc rec.sport.baseball talk.religion.misc rec vs sci rec.autos sci.space rec.sport.hockey sci.electronics sci vs talk sci.med talk.religion.misc sci.space talk.politics.mideast 其次,由于 20News Groups 文本数据集的特 征数很大,为了实验的方便,用主元分析法对数 据集的特征做降维预处理,取前 100 维构成新 的实验数据。 4.2 少量目标域训练样本上的实验结果与分析 实验中取 源 域 中 的 全 部 数 据, 分 别 取 目 标 域中的 1% 、5% 、10%的数据训练 TL⁃MPM 算法 分类器和 MPM 算法分类器。 在 T⁃MPM 和 TL⁃ MPM 算法中的核函数都选取高斯核函数,参数 σ 在 (0.001,0.01,0.1,1,10,100,1 000)中选取。 TL⁃MPM 算法中的参数在(0.001,0.01,0.1,1,10,100,1 000)中 选取。 对表 3 处理好的 6 个真实分类数据集分别随 机独立重复 10 次实验,选取最优参数下的取值,表 4、 表 5 和表 6 分别记录了 10 次独立重复实验正确率的 均值。 表 4 目标域样本的 1%训练结果 Table 4 Results of 1%training samples in the target domain/ % 数据集 T⁃LMPM T⁃KMPM LTL⁃MPM KTL⁃MPM comp vs rec 71.71 72.96 72.56 78.42 comp vs sci 66.46 74.16 72.22 76.49 comp vs talk 90.96 99.15 99.48 99.75 rec vs talk 60.51 71.29 66.26 76.14 rec vs sci 62.49 71.00 64.17 76.48 sci vs talk 68.21 77.24 67.98 76.44 表 5 目标域样本的 5%训练结果 Table 5 Results of 5%training samples in the target domain/ % 数据集 T⁃LMPM T⁃KMPM LTL⁃MPM KTL⁃MPM comp vs rec 61.46 80.92 64.19 83.94 comp vs sci 58.72 76.33 63.29 79.56 comp vs talk 94.13 99.41 97.74 99.83 rec vs talk 57.36 76.30 60.80 78.60 rec vs sci 57.12 78.81 57.49 81.50 sci vs talk 57.42 86.34 63.98 86.75 表 6 目标域样本的 10%训练结果 Table 6 Results of 10%training samples in the target domain/ % 数据集 T⁃LMPM T⁃KMPM LTL⁃MPM KTL⁃MPM comp vs rec 76.46 85.51 80.05 86.06 comp vs sci 70.87 84.75 75.00 83.70 comp vs talk 96.16 99.32 98.66 99.69 rec vs talk 65.30 81.64 66.74 81.56 rec vs sci 64.93 84.89 70.17 85.90 sci vs talk 70.49 90.18 72.17 89.09 第 1 期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·89·

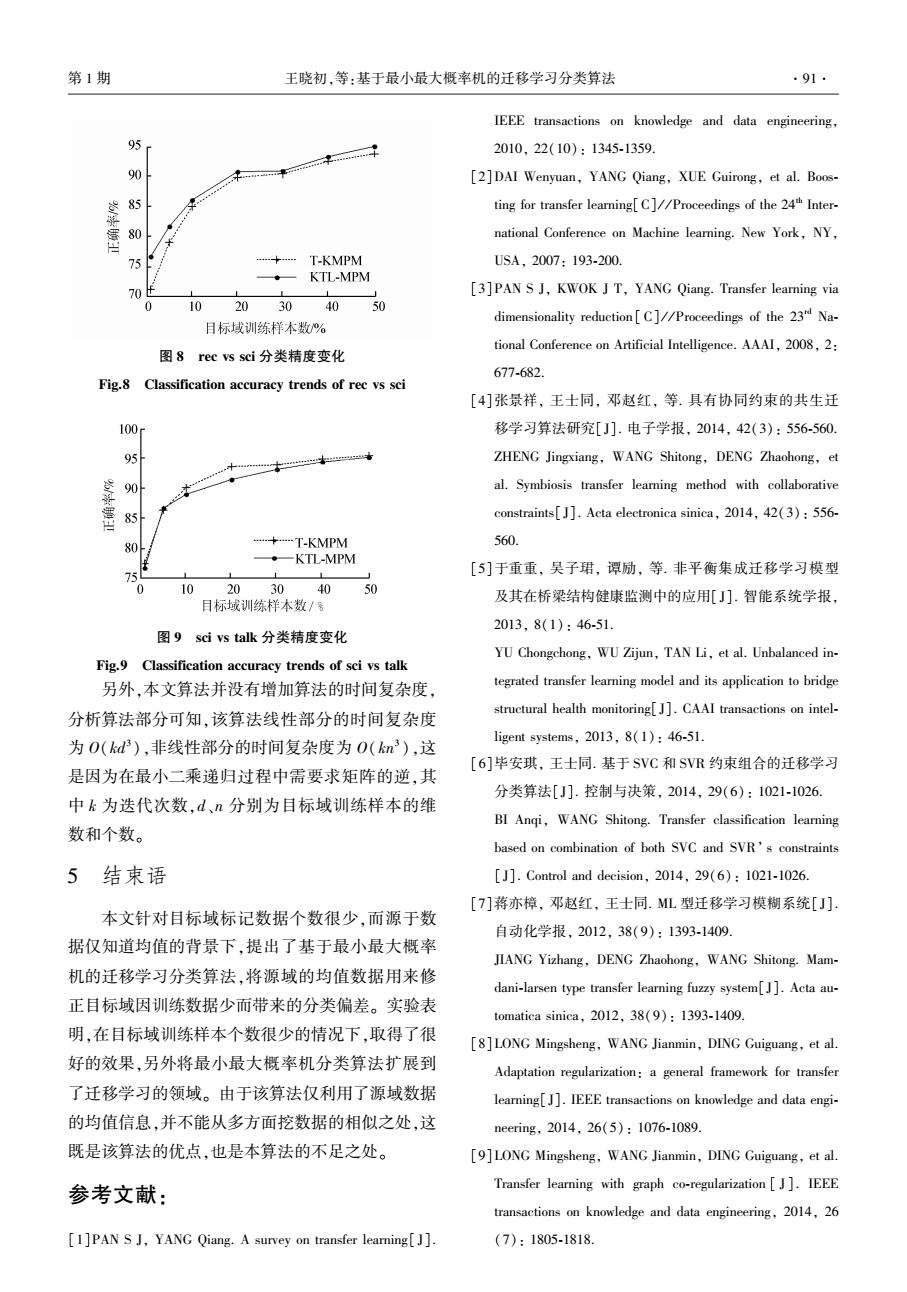
·90. 智能系统学报 第11卷 观察并比较表4、表5、表6中T-LMPM和T- (10%以内),除sci vs talk数据集,其他数据集上 KMPM、LTL-MPM和KTL-MPM的列。发现T- KTL-MPM算法都好于T-KMPM算法,说明样本较 KMPM在各数据集上的分类结果优于T-LMPM, 少时,本文提出算法的优势很明显。在目标域训练 KTL-MPM在各数据集上的分类结果优于LTL 样本增加到一定程度时,两算法的精度差距在逐渐 MPM。说明该真实数据集是非线性的,线性分类方 缩小,最后几乎一致,甚至被T-KMPM算法反超,说 法有一定的局限性。另外,LTL-MPM在各数据集上 明样本增大时,目标域的训练数据的信息越来越多, 的分类结果优于T-LMPM,KTL-MPM在各数据集上 偏差越来越小,迁移过来的源域均值信息已经无法 的分类结果优于T-KMPM,说明源域对目标域的分 矫正该偏差,因为这个偏差已经小于了源域与目标 类起到了一定程度的作用。但提高的多少取决于两 域之间的偏差。这时迁移过来的源域均值信息甚至 域相关性。注意到,在comp vs rec,comp vs sci,rec 转化为了噪声信息,所以精确度反而变低。 vs talk和rec vs sci四个数据集中,本文算法对实验 结果有很大程度的提高,说明在这四类数据集上源 95 域与目标域数据的相似性比较高。在comp vs talk 90 数据集上提高程度很小,说明该数据集上源域和目 标域相似度不高。在sci vs talk数据集上没有提高, 85 反而下降,源域对目标域数据起了反作用,说明该数 -+--T-KMPM 据集上源域和目标域相似度很低。 ·一KTL-MPM 4.3目标域训练样本变化对分类结果的影响 0 10203040 50 少量目标域训练样本上实验说明该真实数据集 目标域训练样本数% 是非线性数据,线性算法并不能很好反应数据的分 图5 comp vs sci分类精度变化 类情况,为了观察TL-MPM算法在样本变化时的有 Fig.5 Classification accuracy trends of comp vs sci 效性,实验中用其非线性算法训练分类器。实验中 100c 取源域中的全部数据,取目标域中的1%、5%、10%、 99 20%、30%、40%、50%的数据训练KTL-MPM算法分 8 类器,取目标域中的1%、5%、10%、20%、30%、40%、 97 50%的数据训练T-KMPM算法分类器。其他设置同 T-KMPM 4.2节。图4~9分别为6个数据集上的实验结果绘 96 ◆—KTL-MPM 制的折线图。 95 0 10 20304050 目标域训练样本数% 95 图6 comp vs talk分类精度变化 90 Fig.6 Classification accuracy trends of comp vs talk oo 中 95 80 90 75 +T-KMPM ·—KTL-MPM 85 70 0 9 203040 50 目标域训练样本数% 75 …+…T-KMPM 一KTL-MPM 图4 comp vs rec分类精度变化 7 0 10 20 30 40 50 Fig.4 Classification accuracy trends of comp vs rec 目标域训练样本数% 观察发现,在目标域训练样本增加时,两种算法 图7 rec ys talk分类精度变化 的精确度都有提高,在目标域训练样本量较少时 Fig.7 Classification accuracy trends of rec vs talk
观察并比较表 4、表 5、表 6 中 T⁃LMPM 和 T⁃ KMPM、 LTL⁃MPM 和 KTL⁃MPM 的 列。 发 现 T⁃ KMPM 在各数据集上的分类结果优于 T⁃LMPM, KTL⁃MPM 在 各 数 据 集 上 的 分 类 结 果 优 于 LTL⁃ MPM。 说明该真实数据集是非线性的,线性分类方 法有一定的局限性。 另外,LTL⁃MPM 在各数据集上 的分类结果优于 T⁃LMPM,KTL⁃MPM 在各数据集上 的分类结果优于 T⁃KMPM,说明源域对目标域的分 类起到了一定程度的作用。 但提高的多少取决于两 域相关性。 注意到,在 comp vs rec,comp vs sci,rec vs talk 和 rec vs sci 四个数据集中,本文算法对实验 结果有很大程度的提高,说明在这四类数据集上源 域与目标域数据的相似性比较高。 在 comp vs talk 数据集上提高程度很小,说明该数据集上源域和目 标域相似度不高。 在 sci vs talk 数据集上没有提高, 反而下降,源域对目标域数据起了反作用,说明该数 据集上源域和目标域相似度很低。 4.3 目标域训练样本变化对分类结果的影响 少量目标域训练样本上实验说明该真实数据集 是非线性数据,线性算法并不能很好反应数据的分 类情况,为了观察 TL⁃MPM 算法在样本变化时的有 效性,实验中用其非线性算法训练分类器。 实验中 取源域中的全部数据,取目标域中的 1%、5%、10%、 20%、30%、40%、50%的数据训练 KTL⁃MPM 算法分 类器,取目标域中的 1%、5%、10%、20%、30%、40%、 50%的数据训练 T⁃KMPM 算法分类器。 其他设置同 4.2 节。 图 4~9 分别为 6 个数据集上的实验结果绘 制的折线图。 图 4 comp vs rec 分类精度变化 Fig.4 Classification accuracy trends of comp vs rec 观察发现,在目标域训练样本增加时,两种算法 的精确度都有提高,在目标域训练样本量较少时 (10%以内),除 sci vs talk 数据集,其他数据集上 KTL⁃MPM 算法都好于 T⁃KMPM 算法,说明样本较 少时,本文提出算法的优势很明显。 在目标域训练 样本增加到一定程度时,两算法的精度差距在逐渐 缩小,最后几乎一致,甚至被 T⁃KMPM 算法反超,说 明样本增大时,目标域的训练数据的信息越来越多, 偏差越来越小,迁移过来的源域均值信息已经无法 矫正该偏差,因为这个偏差已经小于了源域与目标 域之间的偏差。 这时迁移过来的源域均值信息甚至 转化为了噪声信息,所以精确度反而变低。 图 5 comp vs sci 分类精度变化 Fig.5 Classification accuracy trends of comp vs sci 图 6 comp vs talk 分类精度变化 Fig.6 Classification accuracy trends of comp vs talk 图 7 rec vs talk 分类精度变化 Fig.7 Classification accuracy trends of rec vs talk ·90· 智 能 系 统 学 报 第 11 卷
第1期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·91 IEEE transactions on knowledge and data engineering, 95( 2010,22(10):1345-1359. % [2]DAI Wenyuan,YANG Qiang,XUE Guirong,et al.Boos- ting for transfer learning[C]//Proceedings of the 24 Inter- 80 national Conference on Machine learning.New York,NY, +…T-KMPM USA.2007:193-200. KTL-MPM 70E [3]PAN S J,KWOK J T,YANG Qiang.Transfer learning via 0 10 2030 40 50 dimensionality reduction[C]//Proceedings of the 23 Na- 目标域训练样本数% tional Conference on Artificial Intelligence.AAAI,2008,2: 图8 rec vs sci分类精度变化 677-682. Fig.8 Classification accuracy trends of rec vs sci [4]张景祥,王士同,邓赵红,等.具有协同约束的共生迁 100 移学习算法研究[J].电子学报,2014,42(3):556-560. 95 ZHENG Jingxiang,WANG Shitong,DENG Zhaohong,et 90 al.Symbiosis transfer learning method with collaborative 85 constraints[J].Acta electronica sinica,2014,42(3):556- 80 +…T-KMPM 560】 ·一KTL-MPM 75 [5]于重重,吴子珺,谭励,等.非平衡集成迁移学习模型 10 203040 50 目标域训练样本数/ 及其在桥梁结构健康监测中的应用].智能系统学报, 2013,8(1):46-51. 图9 sci vs talk分类精度变化 YU Chongchong,WU Zijun,TAN Li,et al.Unbalanced in- Fig.9 Classification accuracy trends of sci vs talk 另外,本文算法并没有增加算法的时间复杂度, tegrated transfer learning model and its application to bridge 分析算法部分可知,该算法线性部分的时间复杂度 structural health monitoring[J].CAAI transactions on intel- ligent systems,2013,8(1):46-51 为O(kd),非线性部分的时间复杂度为O(n3),这 [6]毕安琪,王士同.基于SVC和SVR约束组合的迁移学习 是因为在最小二乘递归过程中需要求矩阵的逆,其 分类算法[J].控制与决策,2014,29(6):1021-1026. 中k为迭代次数,d、n分别为目标域训练样本的维 BI Anqi,WANG Shitong.Transfer classification learning 数和个数。 based on combination of both SVC and SVR's constraints 5结束语 J].Control and decision,2014,29(6):1021-1026. [7]蒋亦樟,邓赵红,王士同.ML型迁移学习模糊系统[J] 本文针对目标域标记数据个数很少,而源于数 自动化学报,2012,38(9):1393-1409. 据仅知道均值的背景下,提出了基于最小最大概率 JIANG Yizhang,DENG Zhaohong,WANG Shitong.Mam- 机的迁移学习分类算法,将源域的均值数据用来修 dani-larsen type transfer learning fuzzy system[].Acta au- 正目标域因训练数据少而带来的分类偏差。实验表 tomatica sinica,2012,38(9):1393-1409. 明,在目标域训练样本个数很少的情况下,取得了很 [8]LONG Mingsheng,WANG Jianmin,DING Guiguang,et al. 好的效果,另外将最小最大概率机分类算法扩展到 Adaptation regularization:a general framework for transfer 了迁移学习的领域。由于该算法仅利用了源域数据 learning[J].IEEE transactions on knowledge and data engi- 的均值信息,并不能从多方面挖数据的相似之处,这 neering,2014,26(5):1076-1089. 既是该算法的优点,也是本算法的不足之处。 [9]LONG Mingsheng,WANG Jianmin,DING Guiguang,et al. 参考文献: Transfer learning with graph co-regularization [J].IEEE transactions on knowledge and data engineering,2014,26 [1]PAN SJ,YANG Qiang.A survey on transfer learning[J] (7):1805-1818
图 8 rec vs sci 分类精度变化 Fig.8 Classification accuracy trends of rec vs sci 图 9 sci vs talk 分类精度变化 Fig.9 Classification accuracy trends of sci vs talk 另外,本文算法并没有增加算法的时间复杂度, 分析算法部分可知,该算法线性部分的时间复杂度 为 O(kd 3 ),非线性部分的时间复杂度为 O(kn 3 ),这 是因为在最小二乘递归过程中需要求矩阵的逆,其 中 k 为迭代次数,d、n 分别为目标域训练样本的维 数和个数。 5 结束语 本文针对目标域标记数据个数很少,而源于数 据仅知道均值的背景下,提出了基于最小最大概率 机的迁移学习分类算法,将源域的均值数据用来修 正目标域因训练数据少而带来的分类偏差。 实验表 明,在目标域训练样本个数很少的情况下,取得了很 好的效果,另外将最小最大概率机分类算法扩展到 了迁移学习的领域。 由于该算法仅利用了源域数据 的均值信息,并不能从多方面挖数据的相似之处,这 既是该算法的优点,也是本算法的不足之处。 参考文献: [1]PAN S J, YANG Qiang. A survey on transfer learning[ J]. IEEE transactions on knowledge and data engineering, 2010, 22(10): 1345⁃1359. [2]DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Boos⁃ ting for transfer learning[C] / / Proceedings of the 24 th Inter⁃ national Conference on Machine learning. New York, NY, USA, 2007: 193⁃200. [3]PAN S J, KWOK J T, YANG Qiang. Transfer learning via dimensionality reduction[C] / / Proceedings of the 23 rd Na⁃ tional Conference on Artificial Intelligence. AAAI, 2008, 2: 677⁃682. [4]张景祥, 王士同, 邓赵红, 等. 具有协同约束的共生迁 移学习算法研究[J]. 电子学报, 2014, 42(3): 556⁃560. ZHENG Jingxiang, WANG Shitong, DENG Zhaohong, et al. Symbiosis transfer learning method with collaborative constraints[J]. Acta electronica sinica, 2014, 42(3): 556⁃ 560. [5]于重重, 吴子珺, 谭励, 等. 非平衡集成迁移学习模型 及其在桥梁结构健康监测中的应用[ J]. 智能系统学报, 2013, 8(1): 46⁃51. YU Chongchong, WU Zijun, TAN Li, et al. Unbalanced in⁃ tegrated transfer learning model and its application to bridge structural health monitoring[J]. CAAI transactions on intel⁃ ligent systems, 2013, 8(1): 46⁃51. [6]毕安琪, 王士同. 基于 SVC 和 SVR 约束组合的迁移学习 分类算法[J]. 控制与决策, 2014, 29(6): 1021⁃1026. BI Anqi, WANG Shitong. Transfer classification learning based on combination of both SVC and SVR’ s constraints [J]. Control and decision, 2014, 29(6): 1021⁃1026. [7]蒋亦樟, 邓赵红, 王士同. ML 型迁移学习模糊系统[ J]. 自动化学报, 2012, 38(9): 1393⁃1409. JIANG Yizhang, DENG Zhaohong, WANG Shitong. Mam⁃ dani⁃larsen type transfer learning fuzzy system[J]. Acta au⁃ tomatica sinica, 2012, 38(9): 1393⁃1409. [8]LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Adaptation regularization: a general framework for transfer learning[J]. IEEE transactions on knowledge and data engi⁃ neering, 2014, 26(5): 1076⁃1089. [9]LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Transfer learning with graph co⁃regularization [ J ]. IEEE transactions on knowledge and data engineering, 2014, 26 (7): 1805⁃1818. 第 1 期 王晓初,等:基于最小最大概率机的迁移学习分类算法 ·91·

.92. 智能系统学报 第11卷 [10]PERLICH C,DALESSANDRO B,RAEDER T,et al.Ma- [17]BENSOUSSAN A,TEMAM R.Equations aux derivees par- chine learning for targeted display advertising:transfer tielles stochastiques non iineaires[J].Israel journal of learning in action[J].Machine learning,2014,95(1): mathematics,1972,11(1):95-129. 103-127. [18]BOYD S,VANDENBERGHE L,FAYBUSOVICH L.Con- [11 LANCKRIET G R G,EL GHAOUI L,BHATTA- vex optimization[J.IEEE transactions on automatic con- CHARYYA C,et al.A robust minimax approach to clas- ol,2006,51(11):1859 sification[J].The journal of machine learning research, 作者简介: 2003(3):555-582. 王晓初,男,1987年生,硕士研究 [12]ISII K.On the sharpness of Chebyshev-type inequalities 生,主要研究方向为人工智能与模式识 [J].Annals of the institute of statistical mathematics, 别、数字图像处理。 1963(14):185-197. [13]BERTSIMAS D,SETHURAMAN J.Moment problems and semidefinite optimization[M]//WOLKOWICZ H,SAIGAL R.VANDENBERGHE L.Handbook of Semidefinite Pro- gramming.3"ed.US:Springer,2000:469-509. 包芳,女,1970年生,教授,博士,主 [14]CHERNOFF H.The selection of effective attributes for de- 要研究方向为人工智能、模式识别、图 ciding between hypotheses using linear Discriminant func- 像视觉。 tions[C]//The Proceedings of the International Conference on Frontiers of Pattern Recognition.New York,USA, 1972:55-60. 王士同,男,1964年生,教授、博士 「15]陈宝林.最优化理论与算法[M].2版.北京:清华大学 生导师,主要研究方向为人工智能。主 出版社,2005. 持或参加过6项国家自然科学基金项 CHEN Baolin.Optimization theory and algorithm[M].2 目,1项国家教委优秀青年教师基金项 ed.Beijing:Tsinghua University Press,2005. 目,其他省部级科研项目10多项。先 [16]PLAN Y,VERSHYNIN R.Robust 1-bit compressed sens- 后获国家教委、中船总公司和江苏省省 ing and sparse logistic regression:a convex programming 部级科技进步奖5项。发表学术论文近百篇,被$C、EI检 approach[J].IEEE transactions on information theory, 索50余篇。 2012.59(1):482-494
[10]PERLICH C, DALESSANDRO B, RAEDER T, et al. Ma⁃ chine learning for targeted display advertising: transfer learning in action[ J]. Machine learning, 2014, 95( 1): 103⁃127. [ 11 ] LANCKRIET G R G, EL GHAOUI L, BHATTA⁃ CHARYYA C, et al. A robust minimax approach to clas⁃ sification[J]. The journal of machine learning research, 2003(3): 555⁃582. [12] ISII K. On the sharpness of Chebyshev⁃type inequalities [J]. Annals of the institute of statistical mathematics, 1963(14): 185⁃197. [13]BERTSIMAS D, SETHURAMAN J. Moment problems and semidefinite optimization[M] / / WOLKOWICZ H, SAIGAL R, VANDENBERGHE L. Handbook of Semidefinite Pro⁃ gramming. 3 rd ed. US: Springer, 2000: 469⁃509. [14]CHERNOFF H. The selection of effective attributes for de⁃ ciding between hypotheses using linear Discriminant func⁃ tions[C] / / The Proceedings of the International Conference on Frontiers of Pattern Recognition. New York, USA, 1972: 55⁃60. [15]陈宝林. 最优化理论与算法[M]. 2 版. 北京: 清华大学 出版社, 2005. CHEN Baolin. Optimization theory and algorithm[M]. 2 nd ed. Beijing: Tsinghua University Press, 2005. [16]PLAN Y, VERSHYNIN R. Robust 1⁃bit compressed sens⁃ ing and sparse logistic regression: a convex programming approach [ J]. IEEE transactions on information theory, 2012, 59(1): 482⁃494. [17]BENSOUSSAN A, TEMAM R. Equations aux derivees par⁃ tielles stochastiques non iineaires [ J ]. Israel journal of mathematics,1972,11(1):95⁃129. [18]BOYD S, VANDENBERGHE L, FAYBUSOVICH L. Con⁃ vex optimization[ J]. IEEE transactions on automatic con⁃ trol, 2006, 51(11): 1859. 作者简介: 王晓初,男,1987 年生,硕士研究 生,主要研究方向为人工智能与模式识 别、数字图像处理。 包芳,女,1970 年生,教授,博士,主 要研究方向为人工智能、模式识别、图 像视觉。 王士同,男,1964 年生,教授、博士 生导师,主要研究方向为人工智能。 主 持或参加过 6 项国家自然科学基金项 目,1 项国家教委优秀青年教师基金项 目,其他省部级科研项目 10 多项。 先 后获国家教委、中船总公司和江苏省省 部级科技进步奖 5 项。 发表学术论文近百篇,被 SCI、EI 检 索 50 余篇。 ·92· 智 能 系 统 学 报 第 11 卷