
第10卷第6期 智能系统学报 Vol.10 No.6 2015年12月 CAAI Transactions on Intelligent Systems Dec.2015 D0L:10.11992/is.201507037 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20151110.1354.016.html 数值求解优化问题在活动轮廓模型上的应用 廖翠萃1,李敏2,梁久祯2,廖祖华1 (1.江南大学理学院,江苏无锡214122:2.江南大学物联网工程学院,江苏无锡214122) 摘要:针对活动轮廓模型图像分割过程中迭代次数多,分割速度慢的问题,提出一种高阶的数值求解方法。分析 活动轮廓模型中基于全局信息的CV模型,以及基于局部信息的LBF模型,LIF模型。使用二阶、三阶Ruge-Kutta方 法,原始Eulr方法对模型进行数值求解实验对比分析。并对LBF模型中平滑项系数,时间步长的选取进行讨论。 通过对非同质图像、同质图像的实验结果分析表明,所采用的数值方法能够有效地提高数值收敛精度、减少迭代次 数、计算效率高。对不同系数和时间步长,数值方法也能表现出较好的稳定性。 关键词:CV模型;LBF模型;Runge--Kuta方法;数值求解优化;图像分割 中图分类号:TP391.41文献标志码:A文章编号:1673-4785(2015)06-0886-07 中文引用格式:廖翠萃,李敏,梁久祯,等.数值求解优化问题在活动轮廓模型上的应用[J】.智能系统学报,2015,10(6):886-892. 英文引用格式:LIAO Cuicui,LI Min,LIANG Jizhen,etal.Application of a numerical solution to the optimization problem in the active contour model[J].CAAI Transactions on Intelligent Systems,2015,10(6):886-892. Application of a numerical solution to the optimization problem in the active contour model LIAO Cuicui',LI Min2,LIANG Jiuzhen2,LIAO Zuhua' (1.Department of Information and Computaion Science,College of Science,Jiangnan University,Wuxi 214122,China;2.Institute of Intelligent Systems and Network Computing,School of Interet of Things Engineering,Jiangnan University,Wuxi 214122,China) Abstract:In this paper,we analyze numerical optimization procedures and propose high-order numerical methods to deal with the problems of slow convergence and low efficiency in the active contour model.First,we analyze the global information region-based active contour Chan-Vese (CV)model,the local information region-based local bi- nary fitting (LBF)model,and the local image fitting (LIF)model.Then,we compare and analyze image segment results utilizing second-and third-order explicit Runge-Kutta methods,and the standard explicit Euler method.We also analyze the segment results of different sliding coefficient parameters and time steps of the LBF model.The ex- perimental results for the intensity inhomogeneities and common images show that the proposed numerical methods can reduce the number of iterations,and improve convergence accuracy and computational efficiency.In addition, for different coefficients and time steps,the proposed methods yield greater stability. Keywords:CV model;LBF model;Runge-Kutta method;numerical optimization procedure;image segment 活动轮廓模型)图像分割方法近年来得到了 像区域信息的Chan-Vese(CV)模型2),主要是依赖 很好的发展,大体可分为基于图像边界信息的分割 于图像全局的灰度信息,再使用曲线演化理论和水 和基于图像区域信息的分割模型2种。其中基于图 平集方法。模型的求解过程可以转化为寻找能量泛 函的极小值问题,通常采用显示欧拉的数值求解方 收稿日期:2015-04-30.网络出版日期:2015-11-10. 法[),通过变分法得到能量泛函的Euler-Lagrange 基金项目:国家自然科学基金资助项目(11401259):中央高校基本科研 业务费专项资金资助项目(ju5r11407) 方程,最后用有限差分方法进行迭代求解。 通信作者:廖翠萃.E-mail:cliao(@jiangnan.cd.cn CV模型中水平集函数增加了其计算量,存在
第 10 卷第 6 期 智 能 系 统 学 报 Vol.10 №.6 2015 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2015 DOI:10.11992 / tis.201507037 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20151110.1354.016.html 数值求解优化问题在活动轮廓模型上的应用 廖翠萃1 ,李敏2 ,梁久祯2 ,廖祖华1 (1.江南大学 理学院, 江苏 无锡 214122; 2. 江南大学 物联网工程学院,江苏 无锡 214122) 摘 要:针对活动轮廓模型图像分割过程中迭代次数多,分割速度慢的问题,提出一种高阶的数值求解方法。 分析 活动轮廓模型中基于全局信息的 CV 模型,以及基于局部信息的 LBF 模型,LIF 模型。 使用二阶、三阶 Runge⁃Kutta 方 法,原始 Euler 方法对模型进行数值求解实验对比分析。 并对 LBF 模型中平滑项系数,时间步长的选取进行讨论。 通过对非同质图像、同质图像的实验结果分析表明,所采用的数值方法能够有效地提高数值收敛精度、减少迭代次 数、计算效率高。 对不同系数和时间步长,数值方法也能表现出较好的稳定性。 关键词:CV 模型;LBF 模型;Runge⁃Kutta 方法;数值求解优化;图像分割 中图分类号:TP391.41 文献标志码:A 文章编号:1673⁃4785(2015)06⁃0886⁃07 中文引用格式:廖翠萃,李敏,梁久祯,等. 数值求解优化问题在活动轮廓模型上的应用[J]. 智能系统学报, 2015, 10(6): 886⁃892. 英文引用格式:LIAO Cuicui,LI Min,LIANG Jizhen,et al. Application of a numerical solution to the optimization problem in the active contour model[J]. CAAI Transactions on Intelligent Systems, 2015, 10(6): 886⁃892. Application of a numerical solution to the optimization problem in the active contour model LIAO Cuicui 1 , LI Min 2 , LIANG Jiuzhen 2 , LIAO Zuhua 1 (1. Department of Information and Computaion Science, College of Science, Jiangnan University, Wuxi 214122, China; 2. Institute of Intelligent Systems and Network Computing, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China) Abstract:In this paper, we analyze numerical optimization procedures and propose high⁃order numerical methods to deal with the problems of slow convergence and low efficiency in the active contour model. First, we analyze the global information region⁃based active contour Chan⁃Vese (CV) model, the local information region⁃based local bi⁃ nary fitting (LBF) model, and the local image fitting (LIF) model. Then, we compare and analyze image segment results utilizing second⁃and third⁃order explicit Runge⁃Kutta methods, and the standard explicit Euler method. We also analyze the segment results of different sliding coefficient parameters and time steps of the LBF model. The ex⁃ perimental results for the intensity inhomogeneities and common images show that the proposed numerical methods can reduce the number of iterations, and improve convergence accuracy and computational efficiency. In addition, for different coefficients and time steps, the proposed methods yield greater stability. Keywords: CV model; LBF model; Runge⁃Kutta method; numerical optimization procedure; image segment 收稿日期:2015⁃04⁃30. 网络出版日期:2015⁃11⁃10. 基金项目:国家自然科学基金资助项目(11401259);中央高校基本科研 业务费专项资金资助项目(jusrr11407). 通信作者:廖翠萃. E⁃mail:cliao@ jiangnan.edu.cn. 活动轮廓模型[1] 图像分割方法近年来得到了 很好的发展,大体可分为基于图像边界信息的分割 和基于图像区域信息的分割模型 2 种。 其中基于图 像区域信息的 Chan⁃Vese(CV)模型[2] ,主要是依赖 于图像全局的灰度信息,再使用曲线演化理论和水 平集方法。 模型的求解过程可以转化为寻找能量泛 函的极小值问题,通常采用显示欧拉的数值求解方 法[3] ,通过变分法得到能量泛函的 Euler⁃Lagrange 方程,最后用有限差分方法进行迭代求解。 CV 模型中水平集函数增加了其计算量,存在

第6期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·887- 着耗时长、效率低以及易于陷入局部极小值等问题。 式中:c1c2为活动轮廓线内部和外部的强度均值: 针对模型的改进,李春明等提出的处理强度不均 I(x,y)H(中(x,y))dxdy 匀图像的局部二元拟合模型:此外,潘改等)结合 c1= (3) 了LBF模型和GAC活动轮廓模型这2种方法,能有 [K·H(中(x,y))drdy 效地处理弱边界图像的分割:张开华等[)提出的局 部图像拟合模型,基于高斯滤波的变分水平集方法 ,1-66,)dd 来处理强度不均匀的图像分割:刘瑞娟等)提出的 C2= (4) 融合局部和全局信息的活动轮廓模型方法;王小峰 K·(1-H(中(x,y)))dxdy 等]提出了一种局部CV活动模型,将局部图像信 式中:H(·)为Hessian函数。最终的分割轮廓线C 息融入到模型中。对于数值求解方面的改进,如牛 的位置及未知常量c1、c2通过最优化能量泛函得到: 顿方法、与置信域相结合的一般牛顿方法[)以及在 E{C°,c,°,c}=Minc.eE(C,c,cz)(5) 此基础上的改进牛顿方法。此外还有二阶、三阶 1.2基于局部区域信息的LBF模型及LIF模型 Runge-Kutta方法[o在CV模型上的应用。这些算 李春明等4)提出的局部二元拟合模型,有效地 法都能有效地增加了模型的求解速度,并针对不同 解决了C-V模型难以准确分割强度不均匀图像的 的问题都有所改进。目前,CV模型被广泛地应用 问题,该模型使用了图像的局部信息,引入一个以高 于医学图像分割,并具有很好的发展前景。 斯函数为核函数的局部二值拟合能量泛函代替C-V 本文在优化模型的同时,主要对模型的数值求 模型的全局二值拟合能量项.对于任意像素点x, 解过程进行分析改进。首先,分析活动轮廓模型中 x∈2,其拟合项能量泛函: 基于全局信息的CV模型,以及基于局部信息的 FImE K(x-y)*1I(y)-fi(x)dy+ LBF模型、LIF模型。使用二阶、三阶Runge-Kuta inside(C) 方法,并与Euler方法进行对比实验。主要围绕LBF K.(x-y)*1I(y)-f5(x)12dy(6) 模型中平滑项系数,时间步长的选取进行讨论。最 outside(C) 后通过对非同质图像和同质灰度图像的实验结果分 式中:轮廓曲线将图像分为区域内和区域外。(x) 和f,(x)分别为像素点x在区域内和区域外的灰度 析表明,该模型能够有效地提高数值求解的迭代次 拟合值,具体由像素点x邻域内各个像素点所确定。 数,计算效率高,对不同系数,时间步长的稳定性好。 K(x-y)是标准差为σ的高斯核函数,通常取式 1活动轮廓模型 (7)表达式: 1.1基于全局区域信息的CV模型 K,(x-y)=- (7) 经典CV模型[s)是简化Mumford-Shah模型,由 20p(~ 2σ2 学者Chan和Vese提出的一种利用图像区域信息的 当σ的取值过大时,计算量增大:而σ的取值 灰度图像分割方法。在能量泛函中添加了面积项 过小时,获取局部区域灰度变化信息的能力降低,一 Area(inside(C))和Mumford-Shah模型中原有的长 般取5。 度项Length(C)一起推动演化曲线到达分割物体 关于嵌入函数φ(·)的能量泛函最小值得到 的边界。求解过程中使用变分水平集方法,最小化 f(x)和f(x): 能量泛函,通过Euler-Lagrange方法进行迭代数值求 f(x)= K.(x-y)*[H。(P(x))I(x)] (8) 解。定义能量泛函为 K。(x-y)*H(p(x)) E(c1,c2,C)=nu Length(C)+ f3(x)= K,-)*[1,(e()1x)](9) y·Area(inside(C))+F (1) K.(x-y)*(1-H(p(x))) 式中:u,y≥0为权重系数,1(x,y)为待分割图 局部图像拟合(LIF)模型是基于LBF提出的改 像,Length(C)表示边界曲线C的长度项, 进区域活动轮廓模型,利用分片光滑函数近似待分 Area(inside(C))为曲线C的内部区域的面积项, 割图像。与LBF模型相类似,LF模型采用了像素 F为活动轮廓线运动的基于全局信息的拟合项: 点和邻域像素点差值来拟合能量。最后采用高斯滤 波器,使得模型对噪声具有较好的鲁棒性和平滑性。 Fm=+入,lo(x,y)-c,dxdy+ 其能量泛函的水平集形式可以表示: inside (C) 入, I 1o(x,y)-c21'dxdy (2) EF(中)= 211)-1(x)12d (10) outside(C)
着耗时长、效率低以及易于陷入局部极小值等问题。 针对模型的改进,李春明等[4] 提出的处理强度不均 匀图像的局部二元拟合模型;此外,潘改等[5] 结合 了 LBF 模型和 GAC 活动轮廓模型这 2 种方法,能有 效地处理弱边界图像的分割;张开华等[6] 提出的局 部图像拟合模型,基于高斯滤波的变分水平集方法 来处理强度不均匀的图像分割;刘瑞娟等[7] 提出的 融合局部和全局信息的活动轮廓模型方法;王小峰 等[8]提出了一种局部 CV 活动模型,将局部图像信 息融入到模型中。 对于数值求解方面的改进,如牛 顿方法、与置信域相结合的一般牛顿方法[9] 以及在 此基础上的改进牛顿方法。 此外还有二阶、三阶 Runge⁃Kutta 方法[10] 在 CV 模型上的应用。 这些算 法都能有效地增加了模型的求解速度,并针对不同 的问题都有所改进。 目前,CV 模型被广泛地应用 于医学图像分割,并具有很好的发展前景。 本文在优化模型的同时,主要对模型的数值求 解过程进行分析改进。 首先,分析活动轮廓模型中 基于全局信息的 CV 模型,以及基于局部信息的 LBF 模型、LIF 模型。 使用二阶、三阶 Runge⁃Kutta 方法,并与 Euler 方法进行对比实验。 主要围绕 LBF 模型中平滑项系数,时间步长的选取进行讨论。 最 后通过对非同质图像和同质灰度图像的实验结果分 析表明,该模型能够有效地提高数值求解的迭代次 数,计算效率高,对不同系数,时间步长的稳定性好。 1 活动轮廓模型 1.1 基于全局区域信息的 CV 模型 经典 CV 模型[5] 是简化 Mumford⁃Shah 模型,由 学者 Chan 和 Vese 提出的一种利用图像区域信息的 灰度图像分割方法。 在能量泛函中添加了面积项 Area (inside (C) ) 和 Mumford⁃Shah 模型中原有的长 度项 Length(C) 一起推动演化曲线到达分割物体 的边界。 求解过程中使用变分水平集方法,最小化 能量泛函,通过 Euler⁃Lagrange 方法进行迭代数值求 解。 定义能量泛函为 E c1 ,c ( 2 ,C) = nu·Length(C) + γ·Area (inside (C) ) + F cv (1) 式中: μ,γ ≥ 0 为权重系数, I0 (x,y) 为待分割图 像, Length(C) 表 示 边 界 曲 线 C 的 长 度 项, Area (inside (C) ) 为曲线 C 的内部区域的面积项, F cv 为活动轮廓线运动的基于全局信息的拟合项: F cv = + λ1 ∫ inside (C ) I0 (x,y) - c1 2 dxdy + λ2 ∫ outside(C) | I0 (x,y) - c2 | 2 dxdy (2) 式中: c1 、c2 为活动轮廓线内部和外部的强度均值: c1 = ∫ Ω I(x,y) H(ϕ(x,y) ) dxdy ∫ Ω K·H(ϕ(x,y) ) dxdy (3) c2 = ∫ Ω I(x,y) (1⁃H(ϕ(x,y) ) ) dxdy ∫ Ω K·(1⁃H(ϕ(x,y) ) ) dxdy (4) 式中: H(·) 为 Hessian 函数。 最终的分割轮廓线 C 的位置及未知常量 c1 、c2 通过最优化能量泛函得到: E C 0 ,c1 0 ,c2 0 { } = MinC,c1 c2 E C,c1 ,c2 ( ) (5) 1.2 基于局部区域信息的 LBF 模型及 LIF 模型 李春明等[4]提出的局部二元拟合模型,有效地 解决了 C⁃V 模型难以准确分割强度不均匀图像的 问题,该模型使用了图像的局部信息,引入一个以高 斯函数为核函数的局部二值拟合能量泛函代替 C⁃V 模型的全局二值拟合能量项.对于任意像素点 x, x ∈Ω ,其拟合项能量泛函: F LBF x = ∫ inside (C ) Kσ(x - y) ∗ I(y) - f 1(x) 2 dy + ∫ outside(C) Kσ (x - y) ∗ | I(y) - f 2(x) | 2 dy (6) 式中:轮廓曲线将图像分为区域内和区域外。 f 1(x) 和 f 2(x) 分别为像素点 x 在区域内和区域外的灰度 拟合值,具体由像素点 x 邻域内各个像素点所确定。 Kσ(x - y) 是标准差为 σ 的高斯核函数,通常取式 (7)表达式: Kσ (x - y) = 1 2πσ exp ( - (x - y) 2 2 σ 2 ) (7) 当 σ 的取值过大时,计算量增大;而 σ 的取值 过小时,获取局部区域灰度变化信息的能力降低,一 般 σ 取 5。 关于嵌入函数 φ(·) 的能量泛函最小值得到 f 1(x) 和 f 2(x) : f 1 (x) = Kσ (x - y) ∗[Hϕ (φ(x) ) I(x)] Kσ (x - y) ∗ Hϕ (φ(x) ) (8) f 2 (x) = Kσ (x - y) ∗[1⁃Hϕ (φ(x) ) I(x)] Kσ (x - y) ∗ (1⁃Hϕ (φ(x) ) ) (9) 局部图像拟合(LIF)模型是基于 LBF 提出的改 进区域活动轮廓模型,利用分片光滑函数近似待分 割图像。 与 LBF 模型相类似,LIF 模型采用了像素 点和邻域像素点差值来拟合能量。 最后采用高斯滤 波器,使得模型对噪声具有较好的鲁棒性和平滑性。 其能量泛函的水平集形式可以表示: E LIF (ϕ) = 1 2 ∫ Ω | I(x) ⁃ I LIF (x) | 2 dx (10) 第 6 期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·887·

·888· 智能系统学报 第10卷 综上所述,LBF、F模型和C-V模型都是求取全 对于Euler-Lagrange方程的数值求解,传统的方 局最小的能量泛函,因此对乘性噪声都具有良好的抗 法是采用Euler方法,本文将采用二阶、三阶Runge- 噪性,能分割弱边界或者无边界的图像目标,并且初 Kuta方法,这2类数值方法的构造思想如下。 始曲线可设置在图像任意位置。与C-V模型相比, 2.1 Euler方法 LBF方法和LF方法的高斯核函数能获得图像灰度 对于给定的初始条件的微分方程y(t)= 变化的信息,能更准确分割灰度不均匀的图像。LBF ft,y(t)),y(to)=yo,Euler方法迭代求解过程为 方法的能量泛函是以全局误差平方和最小的准则建 y1=y+△t*f,y),n≥0(15) 立起来的,在实际中得到广泛应用。F在LBF的基 式中:f(t,y)为Euler--Lagrange方程。对活动轮廓 础上,对含有噪声图像的处理结果更加理想。 模型数值求解时,Euler方法的格式为 但是,上述模型在分割灰度值不均匀的复杂图 φ°=initial C 像时,真实的目标和背景的误差平方和往往不是全 bm1=中”+△t*L(中"),n=0,1,…,iter 局最小,而是局部最小。因此,模型的能量泛函不能 (16) 准确描述复杂图像的目标和背景的特征,容易产生 式中:iter为迭代次数。Euler方法形式简单、计算速 错误分割,或者陷入局部极小值的情况。本文从数 度快、易于求解,但其在数值精度和数值稳定性方面 值求解优化的角度出发,使用高精度的二阶、三阶 表现较弱。 Runge-Kutta方法,对CV模型、LBF模型、RIF模型 2.2 Runge--Kutta方法 的数值求解进行讨论分析,加快模型的收敛速度,在 二阶Runge-.Kutta可以表示为 更少的迭代次数内得到更为精确的数值解。 =y+△t*ft”,y") 2 数值求解方法 n+1 △t 本文使用二阶、三阶Runge-Kuta方法,对活动 =y+2*)+f,) 轮廓模型中有代表性的CV模型、LBF模型、LIF模 (17) 型的数值求解问题进行讨论分析。 对活动轮廓模型数值求解时,二阶RK格式为 对活动轮廓模型迭代求解时,使用水平集变分 [d°=initial(C) 法对能量泛函求解,原始CV模型及LBF模型能量 b1=中”+△t*L(中) (18) 泛函均可简化写为 b+1=中”+W2(Φ),n=0,l,…,iter E(c1,c2,C)=nu·Length(C)+F拟合项(11) 水平集函数初始化定义为 式中:W,()=合*(亿(0)+L6))。 2 C=0={(x,y)∈2:φ(x,y)=0} 三阶RK格式为 inside(C)=w={(x,y)∈2:中(x,y)>0} [b°=initial(C) outside(C)=2八w={(x,y)∈2:中(x,y)<0} (12) 中m+1=中”+△t*L(中") 变分法最小化能量泛函E使用Heaviside函数: △t (19) (1,z≥0 时=+会*()+) H(z)= (13) (0,z<0 bm*1=中"+W3(b),n=0,1,…,iter 及一维的Dirac函数δ(e)= dH(z) ,使用变分水平集 W(中)= dz 幸(亿(中)+L(6)+2L()。 6 方法对能量泛函极小化,可得Euler-Lagrange方程: Runge-Kuta方法是求解非线性微分方程的重 OE 要数值迭代方法,是Euler方法的一种推广。它提 L(中")= =-8(中) 7中) a她 nu·div 十F拟合项 高了计算收敛精度,缩小截断误差,并且具有更好的 (14) 稳定性。Runge-Kutta方法的导出基于Taylor展开, 计算时,采用正则化函数H(z)= 对所求问题的解具有较好的光滑度,可以使近似公 及6.a)=1. 式达到所需要的阶数,并且能够有效提高方法的精 62+22,6→ 度。计算时使用Euler-Lagrange函数在若干点上函 0代替H(z)和8(z)。 数值的线性组合来构造近似公式,因此会在时间复
综上所述,LBF、LIF 模型和 C⁃V 模型都是求取全 局最小的能量泛函,因此对乘性噪声都具有良好的抗 噪性,能分割弱边界或者无边界的图像目标,并且初 始曲线可设置在图像任意位置。 与 C⁃V 模型相比, LBF 方法和 LIF 方法的高斯核函数能获得图像灰度 变化的信息,能更准确分割灰度不均匀的图像。 LBF 方法的能量泛函是以全局误差平方和最小的准则建 立起来的,在实际中得到广泛应用。 LIF 在 LBF 的基 础上,对含有噪声图像的处理结果更加理想。 但是,上述模型在分割灰度值不均匀的复杂图 像时,真实的目标和背景的误差平方和往往不是全 局最小,而是局部最小。 因此,模型的能量泛函不能 准确描述复杂图像的目标和背景的特征,容易产生 错误分割,或者陷入局部极小值的情况。 本文从数 值求解优化的角度出发,使用高精度的二阶、三阶 Runge⁃Kutta 方法,对 CV 模型、LBF 模型、RIF 模型 的数值求解进行讨论分析,加快模型的收敛速度,在 更少的迭代次数内得到更为精确的数值解。 2 数值求解方法 本文使用二阶、三阶 Runge⁃Kutta 方法,对活动 轮廓模型中有代表性的 CV 模型、LBF 模型、LIF 模 型的数值求解问题进行讨论分析。 对活动轮廓模型迭代求解时,使用水平集变分 法对能量泛函求解,原始 CV 模型及 LBF 模型能量 泛函均可简化写为 E c1 ,c ( 2 ,C) = nu·Length(C) + F拟合项 (11) 水平集函数初始化定义为 C = ∂w = { (x,y) ∈ Ω:ϕ(x,y) = 0} inside (C) = w = { (x,y) ∈ Ω:ϕ(x,y) > 0} outside (C) = Ω\w = { (x,y) ∈ Ω:ϕ(x,y) < 0} ì î í ïï ïï (12) 变分法最小化能量泛函 E 使用 Heaviside 函数: H(z) = 1,z ≥ 0 0,z < 0 { (13) 及一维的 Dirac 函数 δ(z) = dH(z) dz ,使用变分水平集 方法对能量泛函极小化,可得 Euler⁃Lagrange 方程: L ϕ n ( ) = ∂E ∂ϕ = - δ (ϕ) nu·div Ñϕ Ñϕ æ è ç ö ø ÷ + F拟合项 é ë ê ê ù û ú ú (14) 计 算 时, 采 用 正 则 化 函 数 Hε (z) = 1 2 1 + 2 π arctan z ε æ è ç ö ø ÷ æ è ç ö ø ÷ ,及 δε (z) = 1 π · ε ε 2 + z 2 ,ε → 0 代替 H(z) 和 δ(z) 。 对于 Euler⁃Lagrange 方程的数值求解,传统的方 法是采用 Euler 方法,本文将采用二阶、三阶 Runge⁃ Kutta 方法,这 2 类数值方法的构造思想如下。 2.1 Euler 方法 对于给 定 的 初 始 条 件 的 微 分 方 程 y′(t) = f(t,y (t) ) ,y t 0 ( ) = y0 ,Euler 方法迭代求解过程为 y n+1 = y n + △t∗f t n ,y n ( ) ,n ≥ 0 (15) 式中: f t n ,y n ( ) 为 Euler⁃Lagrange 方程。 对活动轮廓 模型数值求解时,Euler 方法的格式为 ϕ 0 = initial C ϕ n+1 = ϕ n + △t∗L ϕ n ( ) ,n = 0,1,…,iter { (16) 式中:iter 为迭代次数。 Euler 方法形式简单、计算速 度快、易于求解,但其在数值精度和数值稳定性方面 表现较弱。 2.2 Runge⁃Kutta 方法 二阶 Runge⁃Kutta 可以表示为 y n+1 ⁃ = y n + △t∗f t n ,y n ( ) y n+1 = y n + △t 2 ∗ f t n ,y n ( ) + f t n+1 ,y n+1 ⁃ ( ( ) ) ì î í ï ï ïï (17) 对活动轮廓模型数值求解时,二阶 RK 格式为 ϕ 0 = initial (C) ϕ n+1 = ϕ n + △t∗L ϕ n ( ) ϕ n+1 = ϕ n + W2 (ϕ) ,n = 0,1,…,iter ì î í ï ï ï ï (18) 式中: W2 (ϕ) = △t 2 ∗ L ϕ n ( ) + L ϕ n+1 ( ( ) ) 。 三阶 RK 格式为 ϕ 0 = initial (C) ϕ n+1 = ϕ n + △t∗L ϕ n ( ) ϕ n+ 1 2 = ϕ n + △t 4 ∗ L ϕ n ( ) + L ϕ n+1 ( ( ) ) ϕ n+1 = ϕ n + W3 (ϕ) ,n = 0,1,…,iter ì î í ï ï ïï ï ï ïï (19) W3 (ϕ) = △t 6 ∗ L ϕ n ( ) + L ϕ n+1 ( ) + 2L ϕ n+ 1 ( ( 2 ) ) 。 Runge⁃Kutta 方法是求解非线性微分方程的重 要数值迭代方法,是 Euler 方法的一种推广。 它提 高了计算收敛精度,缩小截断误差,并且具有更好的 稳定性。 Runge⁃Kutta 方法的导出基于 Taylor 展开, 对所求问题的解具有较好的光滑度,可以使近似公 式达到所需要的阶数,并且能够有效提高方法的精 度。 计算时使用 Euler⁃Lagrange 函数在若干点上函 数值的线性组合来构造近似公式,因此会在时间复 ·888· 智 能 系 统 学 报 第 10 卷

第6期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·889· 杂度上造成线性的倍数增加4。本文采用的显 i5-3470:主频为@3.20GHz:内存为4GB:操作系统为 式二阶三阶Runge-Kutta方法并不会在计算复杂度 Microsoft Windows7 Professional。实验选用的素材参考 上造成过多的影响。 文献[11],采用的评价方法参考文献[12-13]。 对模型中的空间导数项的数值离散采用有限差分 3.1LBF模型的参数讨论 方法。本文选择二阶精度的中心差分方法进行数值的 第1部分的参数讨论分析中,LBF模型对活动 近似求解,对中”进行半点中心差分,其偏导数为 轮廓模型Euler-Lagrange函数,即式(14)的长度项 =u6,= 中w+1中 光滑项系数u值,以及时间步长△t比CV模型, (20) 2h 2h LIF模型更加敏感。因此,本文在式(14)中使用拟 中+1w-2中+中1J 合项FF,即式(6)。分别对LBF模型中的不同时 h2 间步长△t和不同光滑系数项u进行3种数值求 (21) 中12中,+中l 解方法的实验讨论。 3.1.1对光滑系数项nu值的讨论 首先,本文对LBF模型中的时间步长△t和光滑 实验与结果分析 系数项u进行讨论。固定时间步长△t=0.1,对光 本文实验是在Matlab R2011b平台上进行的,所 滑项系数nu=0.001×255×255到nu=0.005×255×255 用的计算机系统配置如下:CPU为Intel(R)Core(TM) 的结果进行讨论。图1~3中iter为模型迭代次数。 0 (a)参数iter=l20(b)参数iter=100(c)参数iter=200(d)参数iter=320(e)参数iter=150 nu=0.001×255×255nu=0.002×255×255nu=0,003×255×255nu=0.004×255×255 nu=0.005×255×255 图1显式Euler方法的图像分割结果 Fig.1 Segment results by explicit Euler method 01 (a)参数iter=120 (b)参数iter=100(c)参数iter=200(d)参数iter=320(e)参数iter=150 nu=0.001×255×255nu=0.002×255×255nu=0.003×255×255nu=0.004×255×255nu=0.005×255×255 图2RK-2方法的图像分割结果 Fig.2 Segment results by RK-2 method 065dsded (a)参数iter=120 (b)参数iter=100(c)参数iter=200(d)参数iter-320(e)参数iter=150 nu=0.001×255×255nu=0.002×255×255nu=0.003×255×255nu=0.004×255×255nu=0.005×255×255 图3RK-3方法的图像分割结果 Fig.3 Segment results by RK-3 method
杂度上造成线性的倍数增加[14⁃15] 。 本文采用的显 式二阶三阶 Runge⁃Kutta 方法并不会在计算复杂度 上造成过多的影响。 对模型中的空间导数项的数值离散采用有限差分 方法。 本文选择二阶精度的中心差分方法进行数值的 近似求解,对 ϕi,j n 进行半点中心差分,其偏导数为 ϕx = ϕi+1,j ⁃ ϕi⁃1,j 2h ϕy = ϕi,j+1 ⁃ ϕi,j⁃1 2h (20) ϕxx = ϕi+1,j ⁃2 ϕi,j + ϕi⁃1,j h 2 ϕyy = ϕi,j+1 ⁃2 ϕi,j + ϕi,j⁃1 h 2 ì î í ï ïï ï ï (21) 3 实验与结果分析 本文实验是在 Matlab R2011b 平台上进行的, 所 用的计算机系统配置如下:CPU 为 Intel(R) Core(TM) i5⁃3470; 主频为@ 3.20 GHz; 内存为 4 GB; 操作系统为 Microsoft Windows7 Professional。 实验选用的素材参考 文献[11],采用的评价方法参考文献[12⁃13]。 3.1 LBF 模型的参数讨论 第 1 部分的参数讨论分析中,LBF 模型对活动 轮廓模型 Euler⁃Lagrange 函数,即式(14) 的长度项 光滑项系数 nu 值,以及时间步长 △t 比 CV 模型, LIF 模型更加敏感。 因此,本文在式(14)中使用拟 合项 F LBF ,即式(6)。 分别对 LBF 模型中的不同时 间步长 △t 和不同光滑系数项 nu 进行 3 种数值求 解方法的实验讨论。 3.1.1 对光滑系数项 nu 值的讨论 首先,本文对 LBF 模型中的时间步长 △t 和光滑 系数项 nu 进行讨论。 固定时间步长 △t = 0.1,对光 滑项系数 nu = 0.001×255×255 到 nu = 0.005×255×255 的结果进行讨论。 图 1~3 中 iter 为模型迭代次数。 图 1 显式 Euler 方法的图像分割结果 Fig.1 Segment results by explicit Euler method 图 2 RK⁃2 方法的图像分割结果 Fig.2 Segment results by RK⁃2 method 图 3 RK⁃3 方法的图像分割结果 Fig.3 Segment results by RK⁃3 method 第 6 期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·889·
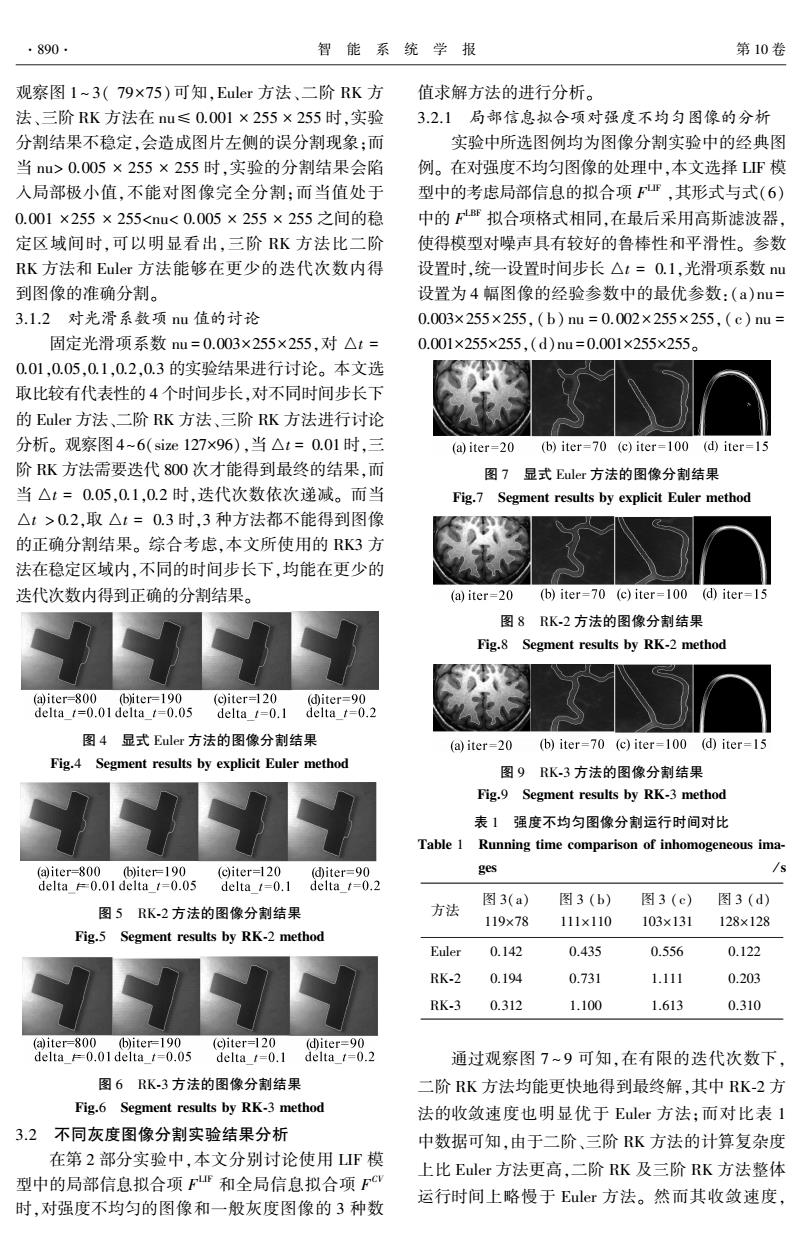
·890· 智能系统学报 第10卷 观察图1~3(79×75)可知,Euler方法、二阶RK方 值求解方法的进行分析。 法、三阶RK方法在nu≤0.001×255×255时,实验 3.2.1局部信息拟合项对强度不均匀图像的分析 分割结果不稳定,会造成图片左侧的误分割现象:而 实验中所选图例均为图像分割实验中的经典图 当nu>0.005×255×255时,实验的分割结果会陷 例。在对强度不均匀图像的处理中,本文选择LF模 入局部极小值,不能对图像完全分割:而当值处于 型中的考虑局部信息的拟合项F,其形式与式(6) 0.001×255×2550.2,取△t=0.3时,3种方法都不能得到图像 的正确分割结果。综合考虑,本文所使用的RK3方 法在稳定区域内,不同的时间步长下,均能在更少的 迭代次数内得到正确的分割结果。 (a)iter=20 (b)iter=70 (c)iter=100 (d)iter=15 图8RK.2方法的图像分割结果 Fig.8 Segment results by RK-2 method (a)iter=800 (biter=190 (c)iter=120 (d)iter=90 delta t=0.01 delta t=0.05 delta t=0.1 delta t=0.2 图4显式Euler方法的图像分割结果 (a)iter=20 (b)iter=70 (c)iter=100 (d)iter=15 Fig.4 Segment results by explicit Euler method 图9RK-3方法的图像分割结果 Fig.9 Segment results by RK-3 method 表1强度不均匀图像分割运行时间对比 Table 1 Running time comparison of inhomogeneous ima- (a)iter=800 (b)iter=190 (c)iter=120 (d)iter=90 ges /s delta =0.01 delta 1=0.05 delta 1=0.1 delta t=0.2 图3(a) 图3(b) 图3(c) 图3(d) 图5RK-2方法的图像分割结果 方法 119×78 111×110 103×131 128×128 Fig.5 Segment results by RK-2 method Euler 0.142 0.435 0.556 0.122 RK-2 0.194 0.731 1.111 0.203 RK-3 0.312 1.100 1.613 0.310 (a)iter-800 (b)iter=190 (c)iter=120 (d)iter=90 delta =0.01 delta t=0.05 delta t=0.1 delta t=0.2 通过观察图7~9可知,在有限的迭代次数下 图6RK-3方法的图像分割结果 二阶RK方法均能更快地得到最终解,其中RK-2方 Fig.6 Segment results by RK-3 method 法的收敛速度也明显优于Euler方法:而对比表1 3.2不同灰度图像分割实验结果分析 中数据可知,由于二阶、三阶K方法的计算复杂度 在第2部分实验中,本文分别讨论使用F模 上比Euler方法更高,二阶RK及三阶RK方法整体 型中的局部信息拟合项FF和全局信息拟合项F 运行时间上略慢于Euler方法。然而其收敛速度, 时,对强度不均匀的图像和一般灰度图像的3种数
观察图 1 ~ 3( 79×75)可知,Euler 方法、二阶 RK 方 法、三阶 RK 方法在 nu≤ 0.001 × 255 × 255 时,实验 分割结果不稳定,会造成图片左侧的误分割现象;而 当 nu> 0.005 × 255 × 255 时,实验的分割结果会陷 入局部极小值,不能对图像完全分割;而当值处于 0.001 ×255 × 255<nu< 0.005 × 255 × 255 之间的稳 定区域间时,可以明显看出,三阶 RK 方法比二阶 RK 方法和 Euler 方法能够在更少的迭代次数内得 到图像的准确分割。 3.1.2 对光滑系数项 nu 值的讨论 固定光滑项系数 nu = 0.003×255×255,对 △t = 0.01,0.05,0.1,0.2,0.3 的实验结果进行讨论。 本文选 取比较有代表性的 4 个时间步长,对不同时间步长下 的 Euler 方法、二阶 RK 方法、三阶 RK 方法进行讨论 分析。 观察图4~6(size 127×96),当 △t = 0.01 时,三 阶 RK 方法需要迭代 800 次才能得到最终的结果,而 当 △t = 0.05,0.1,0.2 时,迭代次数依次递减。 而当 △t > 0.2,取 △t = 0.3 时,3 种方法都不能得到图像 的正确分割结果。 综合考虑,本文所使用的 RK3 方 法在稳定区域内,不同的时间步长下,均能在更少的 迭代次数内得到正确的分割结果。 图 4 显式 Euler 方法的图像分割结果 Fig.4 Segment results by explicit Euler method 图 5 RK⁃2 方法的图像分割结果 Fig.5 Segment results by RK⁃2 method 图 6 RK⁃3 方法的图像分割结果 Fig.6 Segment results by RK⁃3 method 3.2 不同灰度图像分割实验结果分析 在第 2 部分实验中,本文分别讨论使用 LIF 模 型中的局部信息拟合项 F LIF 和全局信息拟合项 F CV 时,对强度不均匀的图像和一般灰度图像的 3 种数 值求解方法的进行分析。 3.2.1 局部信息拟合项对强度不均匀图像的分析 实验中所选图例均为图像分割实验中的经典图 例。 在对强度不均匀图像的处理中,本文选择 LIF 模 型中的考虑局部信息的拟合项 F LIF ,其形式与式(6) 中的 F LBF 拟合项格式相同,在最后采用高斯滤波器, 使得模型对噪声具有较好的鲁棒性和平滑性。 参数 设置时,统一设置时间步长 △t = 0.1,光滑项系数 nu 设置为 4 幅图像的经验参数中的最优参数:(a)nu = 0.003×255×255,( b) nu = 0.002 × 255 × 255,( c) nu = 0.001×255×255,(d)nu = 0.001×255×255。 图 7 显式 Euler 方法的图像分割结果 Fig.7 Segment results by explicit Euler method 图 8 RK⁃2 方法的图像分割结果 Fig.8 Segment results by RK⁃2 method 图 9 RK⁃3 方法的图像分割结果 Fig.9 Segment results by RK⁃3 method 表 1 强度不均匀图像分割运行时间对比 Table 1 Running time comparison of inhomogeneous ima⁃ ges / s 方法 图 3(a) 119×78 图 3 (b) 111×110 图 3 (c) 103×131 图 3 (d) 128×128 Euler 0.142 0.435 0.556 0.122 RK⁃2 0.194 0.731 1.111 0.203 RK⁃3 0.312 1.100 1.613 0.310 通过观察图 7 ~ 9 可知,在有限的迭代次数下, 二阶 RK 方法均能更快地得到最终解,其中 RK⁃2 方 法的收敛速度也明显优于 Euler 方法;而对比表 1 中数据可知,由于二阶、三阶 RK 方法的计算复杂度 上比 Euler 方法更高,二阶 RK 及三阶 RK 方法整体 运行时间上略慢于 Euler 方法。 然而其收敛速度, ·890· 智 能 系 统 学 报 第 10 卷

第6期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·891- 精确度均比Euler方法更好。 表2一般灰度图像分割运行时间对比数据 3.2.2全局信息拟合项对一般灰度图像的分析 Table 2 Running time comparison of general gray images/s 在对一般灰度图像实验分析时,本文使用式 图4(e) 图4(f) 图4(g) 方法 (2)的全局信息拟合能量项F",对3幅比较有代表 84×84 128×128 256×256 性的一般图像进行实验对比分析。统一设置时间步 Euler 0.030 0.048 0.302 长△t=1,光滑项系数u=0.001×255×255。实验 RK-2 0.034 0.039 0.444 结果如图10~12所示。 RK-3 0.038 0.041 0.602 4 结束语 本文使用高阶数值求解优化方法解决水平集变 (a)iter=2 (b)iter=2 (c)iter=20 分图像分割问题。通过将二阶、三阶Runge-Kutta方 法,与传统Euler方法在基于全局区域信息的CV模 图10显式Euler方法的图像分割结果 型,及基于局部区域信息的LBF、LF模型上实验对 Fig.10 Segment results by explicit Euler method 比分析可知:本文模型对光滑项系数及不同时间步长 的情况下,均能更快地得到实验结果,并有效提高了 分割的精度。实验结果表明,RK-2、RK-3方法的使用 提高了计算精度,减少迭代次数、减小迭代误差,且比 (a)iter=2 (b)iter=2 (c)iter=20 Euler方法具有更好地稳定性。然而RK-2、RK-3方 法在在计算复杂度上比传统Euler方法较为复杂。因 图11RK-2方法的图像分割结果 此,从模型和数值求解优化问题相结合的角度出发, Fig.11 Segment results by RK-2 method 如何选择更优的数值求解方法,以得到更优的实验结 果,将作为今后继续研究发展的一个方向。 参考文献: (a)iter=2 (b)iter=2 (c)iter=20 [1]VESE L A,CHAN T F.A multiphase level set framework 图12RK-3方法的图像分割结果 for image segmentation using the Mumford and Shah model [J].International Journal of Computer Vision,2002,50 Fig.12 Segment results by RK-3 method (3):271-293 从图10(a)、11(a)、11(a)中可以看出,采用 [2]CHAN T F,VESE L A.Active contours without edges[J]. Euler方法,本文二阶、三阶RK方法得到的分割结 IEEE Transactions on Image Processing,2001,10(2): 果类似,均能在2次迭代之后收敛。这里主要是因 266-277. [3]COHEN L D,COHEN I.Finite-element methods for active 为图像的分辨率较小且图像自身简单。此时,3种 contour models and balloons for 2-D and 3-D images[J]. 方法均能得到正确结果:再观察图10(b)、11(b)、 IEEE Transactionson on Pattern Analysis Machine Intelli- 12(b),二阶RK及三阶RK均能得到正确的分割结 gence,.1993,15(11):1131-1147. 果,而Euler方法分割不完全,且带有许多不连续 [4]LI Chunming,KAO C Y,GORE J C,et al.Implicit active 点;对含有大量噪声的图10(c)、11(c)、12(c),3种 contours driven by local binary fitting energy[J].IEEE Con- ference on Computer Vision and Pattern Recognition,2007: 模型的抗噪能力均比较差,在迭代20次时,模型分 1.7. 割都带有大量噪点。也表明了本文方法没有在鲁棒 [5]潘改,高立群,张萍.基于LBF方法的测地线活动轮廓 性上着重改进。观察表2可知,当使用全局能量拟 模型[J].模式识别与人工智能,2013,26(12):1179- 合项时,本文二阶、三阶RK模型,与Euler方法运行 1184 PAN Gai,GAO Liqun,ZHANG Ping.Geodesic active con- 时间相近,且能得到更准确的分割结果。综上所述, tour based on LBF method[J].Pattern Recognition and Ai- 本文方法具有一定的优势。 tificial Intelligence,2013,26(12):1179-1184. [6]ZHANG Kaihua,SONG Huihui,ZHANG Lei.Active con-
精确度均比 Euler 方法更好。 3.2.2 全局信息拟合项对一般灰度图像的分析 在对一般灰度图像实验分析时,本文使用式 (2)的全局信息拟合能量项 F CV ,对 3 幅比较有代表 性的一般图像进行实验对比分析。 统一设置时间步 长 △t = 1,光滑项系数 nu = 0.001×255×255。 实验 结果如图 10~12 所示。 图 10 显式 Euler 方法的图像分割结果 Fig.10 Segment results by explicit Euler method 图 11 RK⁃2 方法的图像分割结果 Fig.11 Segment results by RK⁃2 method 图 12 RK⁃3 方法的图像分割结果 Fig.12 Segment results by RK⁃3 method 从图 10( a)、11( a)、11( a) 中可以看出,采用 Euler 方法,本文二阶、三阶 RK 方法得到的分割结 果类似,均能在 2 次迭代之后收敛。 这里主要是因 为图像的分辨率较小且图像自身简单。 此时,3 种 方法均能得到正确结果;再观察图 10( b)、11( b)、 12(b),二阶 RK 及三阶 RK 均能得到正确的分割结 果,而 Euler 方法分割不完全,且带有许多不连续 点;对含有大量噪声的图 10(c)、11(c)、12(c),3 种 模型的抗噪能力均比较差,在迭代 20 次时,模型分 割都带有大量噪点。 也表明了本文方法没有在鲁棒 性上着重改进。 观察表 2 可知,当使用全局能量拟 合项时,本文二阶、三阶 RK 模型,与 Euler 方法运行 时间相近,且能得到更准确的分割结果。 综上所述, 本文方法具有一定的优势。 表 2 一般灰度图像分割运行时间对比数据 Table 2 Running time comparison of general gray images / s 方法 图 4(e) 84×84 图 4 (f) 128×128 图 4(g) 256×256 Euler 0.030 0.048 0.302 RK⁃2 0.034 0.039 0.444 RK⁃3 0.038 0.041 0.602 4 结束语 本文使用高阶数值求解优化方法解决水平集变 分图像分割问题。 通过将二阶、三阶 Runge⁃Kutta 方 法,与传统 Euler 方法在基于全局区域信息的 CV 模 型,及基于局部区域信息的 LBF、 LIF 模型上实验对 比分析可知:本文模型对光滑项系数及不同时间步长 的情况下,均能更快地得到实验结果,并有效提高了 分割的精度。 实验结果表明,RK⁃2、RK⁃3 方法的使用 提高了计算精度、减少迭代次数、减小迭代误差,且比 Euler 方法具有更好地稳定性。 然而 RK⁃2、RK⁃3 方 法在在计算复杂度上比传统 Euler 方法较为复杂。 因 此,从模型和数值求解优化问题相结合的角度出发, 如何选择更优的数值求解方法,以得到更优的实验结 果,将作为今后继续研究发展的一个方向。 参考文献: [1]VESE L A, CHAN T F. A multiphase level set framework for image segmentation using the Mumford and Shah model [ J]. International Journal of Computer Vision, 2002, 50 (3): 271⁃293. [2]CHAN T F, VESE L A. Active contours without edges[ J]. IEEE Transactions on Image Processing, 2001, 10 ( 2): 266⁃277. [3]COHEN L D, COHEN I. Finite⁃element methods for active contour models and balloons for 2⁃D and 3⁃D images [ J]. IEEE Transactionson on Pattern Analysis Machine Intelli⁃ gence, 1993, 15(11): 1131⁃1147. [4]LI Chunming, KAO C Y, GORE J C, et al. Implicit active contours driven by local binary fitting energy[J]. IEEE Con⁃ ference on Computer Vision and Pattern Recognition, 2007: 1⁃7. [5]潘改, 高立群, 张萍. 基于 LBF 方法的测地线活动轮廓 模型[J]. 模式识别与人工智能, 2013, 26( 12): 1179⁃ 1184. PAN Gai, GAO Liqun, ZHANG Ping. Geodesic active con⁃ tour based on LBF method[J]. Pattern Recognition and Ai⁃ tificial Intelligence, 2013, 26(12): 1179⁃1184. [6] ZHANG Kaihua, SONG Huihui, ZHANG Lei. Active con⁃ 第 6 期 廖翠萃,等:数值求解优化问题在活动轮廓模型上的应用 ·891·

.892. 智能系统学报 第10卷 tours driven by local image fitting energy[]].Pattern Rec- REN Shougang,MA Chao,XU Huanliang.Improved skel- 0 gnition,2010,43(4):1199-1206. eton extracton algorithm based active contour model re- [7]刘瑞娟,何传江,原野.融合局部和全局图像信息的活 search[]].Computer Science,2013,40(7):289-292, 动轮廓模型[J].计算机辅助设计与图形学报,2012,24 296. (3):364-371. [14]CORMEN T H,LEISER C E,RIVEST R L,et al.Intro- LIU Ruijuan,HE Chuanjiang,YUAN Ye.Active contours duction to Algorithms[M].3rd ed.Cambridge,Mass:MIT driven by local and global image fitting energy[J].Journal press,2009:350-400. of Computer-Aided Design Computer Graphics,2012,24 [15 JOHNSON M L.Essential numerical computer methods (3):364-371. [M].Burlington,MA:Academic Press,2010:230-275. [8]WANG Xiaofeng,HUANG Deshuang,XU Huan.An effi- 作者简介: cient local Chan-Vese model for image segmentation [J]. 廖翠萃,女,1983年生,博士,讲 Pattern Recognition,2010,43(3):603-618. 师。发表SCI检索论文4篇、CSCD论 [9]BAR L,SAPIRO G.Generalized Newton-type methods for 文4篇,主持国家自然科学基金项目1 energy formulations in image processing[J].SIAM Journal 项。主要研究方向为保结构数值计算 on Imaging Sciences,2009,2(2):508-531. 方法。 [10]SCHEUERMANN B,ROSENHAHN B.Analysis of numer- ical methods for level set based image segmentation[J]. 李敏,女,1990年生,硕土。发表 Advances in Visual Computing,2009,5876:196-207. [11]LI Chunming,KAO C Y,GORE J C,et al.Minimization CSCD论文一篇,主持江苏省研究生科 研实践项目一项。主要研究方向数字 of region-scalable fitting energy for image segmentation[J]. IEEE Transcations on Image Processing,2008,17(10): 图像处理。 1940-1949. [12]GE Feng,WANG Song,LIU Tiecheng.New benchmark 梁久祯,男,1968生,教授,博士。 for image segmentation evaluation[J].Journal of Electron- ic Imaging,2007,16(3):1010-1016. 主要研究方向为机器视觉、图像处理 [13]任守纲,马超,徐焕良.基于改进主动轮廓模型的图像 等。在专业杂志与国内外会议等发表 分割方法研究[J].计算机科学,2013,40(7):289- 学术论文120余篇,其中被SCI检索8 篇、EI检索33篇.CSCD检索60篇。主 292,296 持国家自然科学基金项目1项、省部级项目3项
tours driven by local image fitting energy[ J]. Pattern Rec⁃ ognition, 2010, 43(4): 1199⁃1206. [7]刘瑞娟, 何传江, 原野. 融合局部和全局图像信息的活 动轮廓模型[J]. 计算机辅助设计与图形学报, 2012, 24 (3): 364⁃371. LIU Ruijuan, HE Chuanjiang, YUAN Ye. Active contours driven by local and global image fitting energy[ J]. Journal of Computer⁃Aided Design & Computer Graphics, 2012, 24 (3): 364⁃371. [8] WANG Xiaofeng, HUANG Deshuang, XU Huan. An effi⁃ cient local Chan⁃Vese model for image segmentation [ J]. Pattern Recognition, 2010, 43(3): 603⁃618. [9]BAR L, SAPIRO G. Generalized Newton⁃type methods for energy formulations in image processing[ J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 508⁃531. [10]SCHEUERMANN B, ROSENHAHN B. Analysis of numer⁃ ical methods for level set based image segmentation [ J]. Advances in Visual Computing, 2009, 5876: 196⁃207. [11]LI Chunming, KAO C Y, GORE J C, et al. Minimization of region⁃scalable fitting energy for image segmentation[J]. IEEE Transcations on Image Processing, 2008, 17( 10): 1940⁃1949. [12] GE Feng, WANG Song, LIU Tiecheng. New benchmark for image segmentation evaluation[J]. Journal of Electron⁃ ic Imaging, 2007, 16(3): 1010⁃1016. [13]任守纲, 马超, 徐焕良. 基于改进主动轮廓模型的图像 分割方法研究[ J]. 计算机科学, 2013, 40 ( 7): 289⁃ 292, 296. REN Shougang, MA Chao, XU Huanliang. Improved skel⁃ eton extracton algorithm based active contour model re⁃ search[ J]. Computer Science, 2013, 40 ( 7): 289⁃292, 296. [14]CORMEN T H, LEISER C E, RIVEST R L, et al. Intro⁃ duction to Algorithms[M]. 3rd ed. Cambridge, Mass: MIT press, 2009: 350⁃400. [15] JOHNSON M L. Essential numerical computer methods [M]. Burlington, MA: Academic Press, 2010: 230⁃275. 作者简介: 廖翠萃, 女, 1983 年生, 博士, 讲 师。 发表 SCI 检索论文 4 篇、CSCD 论 文 4 篇,主持国家自然科学基金项目 1 项。 主要研究方向为保结构数值计算 方法。 李敏, 女, 1990 年生, 硕士。 发表 CSCD 论文一篇,主持江苏省研究生科 研实践项目一项。 主要研究方向数字 图像处理。 梁久祯, 男, 1968 生, 教授,博士。 主要研究方向为机器视觉、图像处理 等。 在专业杂志与国内外会议等发表 学术论文 120 余篇,其中被 SCI 检索 8 篇、EI 检索 33 篇、CSCD 检索 60 篇。 主 持国家自然科学基金项目 1 项、省部级项目 3 项。 ·892· 智 能 系 统 学 报 第 10 卷