
第11卷第5期 智能系统学报 Vol.11 No.5 2016年10月 CAAI Transactions on Intelligent Systems 0ct.2016 D0I:10.11992/is.201510017 网络出版地址:htp:/www.cnki.net/kcms/detail/23.1538.TP.20160824.0929.008.html 基于模糊滑模的多机器人系统编队控制 钱殿伟 (华北电力大学控制与计算机工程学院,北京102206) 摘要:针对多机器人编队控制问题,提出了一种滑模控制与模糊逻辑相结合的控制方法。运用领航一跟随法,建 立机器人系统的动力学模型。该模型具有不确定性,在不确定性上界未知的假设条件下,运用模糊逻辑,设计模糊 补偿器,以逼近系统的不确定性部分。基于Lyapunov理论,证明所设计的模糊滑模编队控制系统具有渐近稳定性, 同时模糊补偿器的逼近误差是收敛的。仿真结果表明,该方法可使多机器人系统迅速地形成所期望的队形,并在运 动中保持该队形。 关键词:多机器人:编队控制:不确定性:滑模控制:模糊逻辑 中图分类号:TP242.6文献标志码:A文章编号:1673-4785(2016)05-0641-07 中文引用格式:钱殿伟.基于模糊滑模的多机器人系统编队控制[J].智能系统学报,2016,11(5):641-647, 英文引用格式:QIAN Dianwei..Formation control of multi-robot systems in a fuzzy sliding mode[J].CAAI transactions on intelli- gent systems,2016,11(5):641-647. Formation control of multi-robot systems in a fuzzy sliding mode QIAN Dianwei (School of Control and Computer Engineering,North China Electric Power University,Beijing 102206,China) Abstract:To resolve the formation problem resulting from a swarm of robots,a control scheme is proposed based on sliding mode control and fuzzy logic.A formation dynamic model is established utilizing the leader -follower ap- proach.The model is subject to uncertainties.If the upper bounds of these uncertainties are unknown,then a fuzzy compensator can be adopted to approximate the uncertainties.From an Lyapunov approach,not only is the sliding- mode-based formation control system asymptotically stable,but the approximate error of the fuzzy compensator is al- so convergent.The simulation results demonstrate that the robots can rapidly form and maintain the desired specified geometrical shapes during movement. Keywords:multi-robot;formation control;uncertainties;sliding model control;fuzzy logic 多机器人编队系统相比复杂单机器人系统具有 性化6、预测控制[)、滑模控制[8及智能控制[0川]等。 诸多优点,在工业制造、地理勘测、太空探索等领域 就模型而言,多机器人编队控制分为基于运动 具有广泛的应用前景,目前已成为研究的热点问题 学模型的控制和基于动力学模型的控制。在实际应 之一。多机器人编队控制方法主要有行为法山、虚 用中,多机器人编队系统受到负载变化、参数摄动、 拟结构法[1、领航一跟随法[4及人工势场法[)等。 测量噪声、摩擦、传动系统的非线性及外部扰动等不 其中,领航一跟随法因其控制简单,易于实现分布式 确定性的影响)。基于模型的控制方法难以克服 控制,可将整个编队控制问题简化为若干独立的轨 不确定的影响,需要探寻更加有效的控制策略。 迹跟踪控制问题,在多机器人编队控制方面应用广 滑模控制具有不变性的特点,因其鲁棒性强、响 泛。采用领航一跟随法,常用的控制算法有反馈线 应快速和易于实现等特点被广泛地研究[6.。在 滑模控制器设计中,为保证控制系统的稳定性,通常 收稿日期:2015-10-22.网络出版日期:2016-08-24 要假设已知不确定性的上界。就多机器人编队控制 基金项目:国家自然科学基金项目(60904008). 通信作者:钱殿伟.E-mail:dianwei.qian@ncepu.cdu.cn. 问题而言,这个假设在实际中可能难以满足。模糊
第 11 卷第 5 期 智 能 系 统 学 报 Vol.11 №.5 2016 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2016 DOI:10.11992 / tis.201510017 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160824.0929.008.html 基于模糊滑模的多机器人系统编队控制 钱殿伟 (华北电力大学 控制与计算机工程学院,北京 102206) 摘 要:针对多机器人编队控制问题,提出了一种滑模控制与模糊逻辑相结合的控制方法。 运用领航—跟随法,建 立机器人系统的动力学模型。 该模型具有不确定性,在不确定性上界未知的假设条件下,运用模糊逻辑,设计模糊 补偿器,以逼近系统的不确定性部分。 基于 Lyapunov 理论,证明所设计的模糊滑模编队控制系统具有渐近稳定性, 同时模糊补偿器的逼近误差是收敛的。 仿真结果表明,该方法可使多机器人系统迅速地形成所期望的队形,并在运 动中保持该队形。 关键词:多机器人;编队控制;不确定性;滑模控制;模糊逻辑 中图分类号:TP242.6 文献标志码:A 文章编号:1673⁃4785(2016)05⁃0641⁃07 中文引用格式:钱殿伟.基于模糊滑模的多机器人系统编队控制[J]. 智能系统学报, 2016, 11(5):641⁃647. 英文引用格式:QIAN Dianwei.Formation control of multi⁃robot systems in a fuzzy sliding mode [ J]. CAAI transactions on intelli⁃ gent systems, 2016,11(5):641⁃647. Formation control of multi⁃robot systems in a fuzzy sliding mode QIAN Dianwei (School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China) Abstract:To resolve the formation problem resulting from a swarm of robots, a control scheme is proposed based on sliding mode control and fuzzy logic. A formation dynamic model is established utilizing the leader – follower ap⁃ proach. The model is subject to uncertainties. If the upper bounds of these uncertainties are unknown, then a fuzzy compensator can be adopted to approximate the uncertainties. From an Lyapunov approach, not only is the sliding⁃ mode⁃based formation control system asymptotically stable, but the approximate error of the fuzzy compensator is al⁃ so convergent. The simulation results demonstrate that the robots can rapidly form and maintain the desired specified geometrical shapes during movement. Keywords:multi⁃robot; formation control; uncertainties; sliding model control; fuzzy logic 收稿日期:2015⁃10⁃22. 网络出版日期:2016⁃08⁃24. 基金项目:国家自然科学基金项目(60904008). 通信作者:钱殿伟.E⁃mail:dianwei.qian@ ncepu.edu.cn. 多机器人编队系统相比复杂单机器人系统具有 诸多优点,在工业制造、地理勘测、太空探索等领域 具有广泛的应用前景,目前已成为研究的热点问题 之一。 多机器人编队控制方法主要有行为法[1] 、虚 拟结构法[2] 、领航—跟随法[3⁃4] 及人工势场法[5] 等。 其中,领航—跟随法因其控制简单,易于实现分布式 控制,可将整个编队控制问题简化为若干独立的轨 迹跟踪控制问题,在多机器人编队控制方面应用广 泛。 采用领航—跟随法,常用的控制算法有反馈线 性化[6] 、预测控制[7] 、滑模控制[8⁃9]及智能控制[10⁃11]等。 就模型而言,多机器人编队控制分为基于运动 学模型的控制和基于动力学模型的控制。 在实际应 用中,多机器人编队系统受到负载变化、参数摄动、 测量噪声、摩擦、传动系统的非线性及外部扰动等不 确定性的影响[3] 。 基于模型的控制方法难以克服 不确定的影响,需要探寻更加有效的控制策略。 滑模控制具有不变性的特点,因其鲁棒性强、响 应快速和易于实现等特点被广泛地研究[6, 10] 。 在 滑模控制器设计中,为保证控制系统的稳定性,通常 要假设已知不确定性的上界。 就多机器人编队控制 问题而言,这个假设在实际中可能难以满足。 模糊

·642· 智能系统学报 第11卷 逻辑具有以任意精度逼近非线性连续函数的能 领航者 力[0,是估计系统中不确定性的可行方法。 针对未知上界的不确定性,本文结合滑模控制 和模糊逻辑,研究了多机器人系统编队控制问题。 首先,根据跟随者与领航者的相对位置与相对相角, 建立编队系统的动力学模型:然后,采用模糊推理系 统逼近系统中的不确定性,设计滑模控制器稳定相 对位置与相对相角,应用Lyapunov条件证明控制系 统的稳定性和逼近误差的收敛性:最后,通过仿真实 跟随者大 验验证所提出方法的有效性。 1系统描述 图1跟随一领航者编队控制模型 本文以半径为r的圆形非完整轮式移动机器人 Fig.1 Leader-follower formation of multiple robots 为对象,其理想运动学和动力学模型见文献[9]。 对相对相角(1)和位置(2)求二阶导,令x= 采用领航-跟随者编队方法,在一组由n个非完整 [x,x2]T=[l,中:]T,得到跟随-领航者编队控制的 移动机器人组成的编队系统中,选机器人讠为领航 动力学模型的状态空间表达式为 者,剩余n-1个为跟随者。在跟随者中,选择跟随 元k=Gue+d(xk,xt,t) (3) 者k与领航者i组成编队控制模型,其结构如图1 所示。 令9=中+0,-0,各参数矩阵描述如下 在图1中,跟随者k与领航者i的相对相角和 相对距离分别为 d(x法,x,t)=G△山4+L(I2+4:):+F法+P法 cos 0 ψt=T+5t-0 (1) rsin G= sin i re0sPk;Lt三 sinψk la=(x-rcos 0)+(y;-y:-rsin 0) -1 (2) yi-y-rsin 0 I2是2×2单位矩阵;Fk=[F,F2]I;P= 式中:t=arctan x:-xg-rc0s0° [P,P2]';4和4,是2×2扰动矩阵; P,=-(Tx-Ta)cos(中t+日:)-(T-T)sin(中k+0)+rTiosing P=[(a)sin(a +0)-()cos()+rcosda F1=w2l+2ψ0,lu+lt-rcos92-(y0-y0)cos(ψu+9)-(x,0:-元0)sin(中u+0:) F,=[-(0。-i,)sim(a+0)-(。-)eos(a+9)-用asin中」 [(y-y)cos(中+0:)-(-x)sin(ψt+0:)-cos中t)] 式中:πs、T、π、π、和π0∈R分别为领航者示。在图2中,输人向量a=[a1a2…am]I∈U,输 和跟随者的不确定性。 出向量b=[b,b2…bn]'∈V,第l条模糊规则为 建模中主要假设为:领航者与跟随者之间无通 R:If a is Af,a is A,..and a is A 讯延迟:领航者与跟随者均可知自身位置和速度:领 then b1isB1,b2isB,…and b is B。 航者通过通讯将其位置和速度传递给跟随者。 式中:4(p=1,2,…,m)和B(q=1,2,…,n)分别为 2控制系统设计及稳定性分析 第1条规则中语言变量的模糊集合。采用单值模糊 器、乘积模糊机和中心平均解模糊器,则FS的第q 2.1模糊补偿器的设计 个输出为 模糊推理系统(FIS)的数学本质是从集合 U∈Rm到V∈R"的非线性映射,其结构图如图2所 6,=∑6,5(a)=85(a) (4)
逻辑具有以任意精度逼近非线性连续函数的能 力[10] ,是估计系统中不确定性的可行方法。 针对未知上界的不确定性,本文结合滑模控制 和模糊逻辑,研究了多机器人系统编队控制问题。 首先,根据跟随者与领航者的相对位置与相对相角, 建立编队系统的动力学模型;然后,采用模糊推理系 统逼近系统中的不确定性,设计滑模控制器稳定相 对位置与相对相角,应用 Lyapunov 条件证明控制系 统的稳定性和逼近误差的收敛性;最后,通过仿真实 验验证所提出方法的有效性。 1 系统描述 本文以半径为 r 的圆形非完整轮式移动机器人 为对象,其理想运动学和动力学模型见文献[ 9]。 采用领航-跟随者编队方法,在一组由 n 个非完整 移动机器人组成的编队系统中,选机器人 i 为领航 者,剩余 n-1 个为跟随者。 在跟随者中,选择跟随 者 k 与领航者 i 组成编队控制模型,其结构如图 1 所示。 在图 1 中,跟随者 k 与领航者 i 的相对相角和 相对距离分别为 ψik = π + ζik - θi (1) l ik = (xi - xk - rcos θk) 2 + (yi - yk - rsin θk) 2 (2) 式中:ζik = arctan yi -yk -rsin θk xi -xk -rcos θk 。 图 1 跟随—领航者编队控制模型 Fig.1 Leader⁃follower formation of multiple robots 对相 对 相 角 ( 1) 和 位 置 ( 2) 求 二 阶 导, 令 xik = [x1 x2 ] T = [l ik ψik ] T ,得到跟随-领航者编队控制的 动力学模型的状态空间表达式为 x ¨ ik = Gikuk + dik(xik,x · ik,t) (3) 令 φik =ψik +θi -θk ,各参数矩阵描述如下 dik(xik,x · ik,t) = GikΔkuk + Lik(I2 + Δi)ui + Fik + Pik Gik = cos φik rsin φik - sin φik l ik rcos φik l ik é ë ê ê êê ù û ú ú úú ;Lik = - cos ψik 0 sin ψik l ik - 1 é ë ê ê êê ù û ú ú úú ; I2 是 2 × 2 单 位 矩 阵; Fik = [F1 F2 ] T ; Pik = [P1 P2 ] T ;Δk 和Δi 是 2×2 扰动矩阵; P1 = - (πix - πkx)cos(ψik + θi) - (πiy - πky)sin(ψik + θi) + rπkθ sinφik P2 = [(πix - πky)sin(ψik + θ) - (πiy - πky)cos(ψik + θi) + rπkθ cosϕik - l ikπiθ] l ik F1 = ψ ·2 ik l ik + 2ψ · ik θ · i l ik + θ · i 2 l ik - rcos φik θ · k 2 - (y · k θ · k - y · i θ · i)cos(ψik + θi) - (x · i θ · i - x · k θ · k)sin(ψik + θi) F2 = [ - (y · kϕ · ik - ψ · ik y · i)sin(ψik + θi) - (x · kϕ · ik - ψ · ik x · )cos(ψik + θi) - rθ · kϕ · ik sin ϕik] l ik + [l · ik((y · i - y · k)cos(ψik + θi) - (x · i - x · k)sin(ψik + θi) - rθ · k cos ϕik)] l 2 ik 式中:πkx、πky、πkθ、πix、πiy和 πiθ∈R 1 分别为领航者 和跟随者的不确定性。 建模中主要假设为:领航者与跟随者之间无通 讯延迟;领航者与跟随者均可知自身位置和速度;领 航者通过通讯将其位置和速度传递给跟随者。 2 控制系统设计及稳定性分析 2.1 模糊补偿器的设计 模糊 推 理 系 统 ( FIS) 的 数 学 本 质 是 从 集 合 U∈R m 到 V∈R n的非线性映射,其结构图如图 2 所 示。 在图 2 中,输入向量 a = [ a1 a2… am ] T∈U,输 出向量 b = [b1 b2… bn ] T∈V,第 l 条模糊规则为 Rl:If a1 is A l 1 ,a2 is A l 2 , … and am is A l m , then b1 is B l 1 ,b2 is B l 2 ,… and bm is B l n 。 式中:A l p(p = 1,2,…,m)和 B l q(q = 1,2,…,n)分别为 第 l 条规则中语言变量的模糊集合。 采用单值模糊 器、乘积模糊机和中心平均解模糊器,则 FIS 的第 q 个输出为 bq = ∑ M l = 1 b - q ξl(a) = Θ T q ξ(a) (4) ·642· 智 能 系 统 学 报 第 11 卷

第5期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·643· Θ°=a罗min[sp‖d(xd8)-da(法dt,)] 5(a) (8) 式中X。为包含日的有界集合。 定义逼近误差的最小值向量为 p=d(x,x|⊙°)-dt(xt,xt,t)(9) 式中p=[P1P2]T∈R21。 针对多机器人编队设计的FIS是一个4输入2 输出系统,输入变量具有5个模糊子集,所以FIS的 反模糊化 规则库有54条模糊规则,即M=625。 规则化 模糊化 2.2滑模控制器的设计 图2模糊推理系统结构图 定义滑模面 Fig.2 Structure of the FIS Sik(t)=xk+Axik (10) 式中:专(a)=[5(a)52(a)…专w(a)]',8,= 式中:S(t)=[st,(t)s法,2(t)]T∈Rx1,x4=x4-x∈ [0,及…]T,且O,为参数矩阵O的第g R2x1为跟踪误差向量,x#为期望轨迹向量,入为一个 2×2的正定矩阵。 列,M为模糊规则总数。专(a)是模糊基函数向量, 定义参考向量 其中的第!个元素可表示为 6(t)=x4(t)-rt(t) (11) Π=g(a,) (a)= (5) 设计滑模控制律 言(-(o,) u=-Ga[da(x,)-6 +ksa+nsign(sa)] 式中u4(a,)为高斯型隶属函数。 (12) 式中:K和)均为2×2的对角矩阵,即k=diag(K1, y(an)=exp (6) 202 K2),n=diag(n1,n2),其中K1K2n1和72为设计参 式中c,和σ,分别代表此隶属函数的中心和宽度。 数;sign(st)=[sign(sk,1)sign(s法.2)]T,sign(·)为 针对多机器人编队设计FIS,FIS的输入为a= 符号函数。 2.3稳定性证明 [l4中i少]T,FIS的输出为不确定性的逼近值, 定理1对于机器人编队系统式(5),设计模糊 即b=d(xk,x法,t)。 补偿器式(7)和滑模控制律式(12)。如定义参数自 FIS的输入与输出变量均模糊化为负大(NB), 适应律为 负小(NS),零(Z0),正小(PS)和正大(PB)5个模 糊子集,即A=B。={NB,NS,Z0,PS,PB}。所设计 O,=gsk.5(xt,xt) (13) 的FIS第l条模糊规则如下: 式中:T,>0eR,K,>0,n>lp,1(q=1,2),那么多机 R:If lais A,ψisA2,ais As andψtisA4, 器人编队控制系统式(5)是渐近稳定的。 证明选取李雅普诺夫函数: then b is Bi and b2 is B2. 根据式(4),不确定性的逼近值可描述为 (0)=2(ssa+立0gr0,) (14) 9=1 da(x) d4(x4,x4⊙)= 式中:⊙,=⊙-⊙,⊙,代表最优参数矩阵0°的第 da2(x) q列向量。对式(14)求一阶导可得 (7) ig(xa,xa) ⊙5(xt,x)= ()=ss4+∑0T,a (15) 85(x,c)」 g=1 由式(10)和式(11)可知 式中:参数矩阵日ER2,专(xk,在)∈R21。 $张=法-6 (16) 设0存在最优参数矩阵日·,且⊙·满足 将式(3)和式(16)依次代入式(15)可得
图 2 模糊推理系统结构图 Fig.2 Structure of the FIS 式中: ξ ( a) = [ ξ1 ( a) ξ2 ( a) … ξM ( a)] T , Θq = [b 1 q b 2 q … b M q ] T ,且 Θq 为参数矩阵 ΘM×n 的第 q 列,M 为模糊规则总数。 ξ( a) 是模糊基函数向量, 其中的第 l 个元素可表示为 ξl(a) = Π m p = 1μAl p (ap) ∑ M l = 1 (Π m p = 1μAl p (ap)) (5) 式中 μAl p (ap)为高斯型隶属函数。 μAl p (ap) = exp - (ap - cp) 2 2σ 2 p æ è ç ö ø ÷ (6) 式中 cp 和 σp 分别代表此隶属函数的中心和宽度。 针对多机器人编队设计 FIS,FIS 的输入为 a = [l ik ψik l · ik ψ · ik] T ,FIS 的输出为不确定性的逼近值, 即b = d ^ ik(xik,x · ik,t)。 FIS 的输入与输出变量均模糊化为负大(NB), 负小(NS),零( ZO),正小( PS) 和正大( PB) 5 个模 糊子集,即 A l p =B l p = {NB, NS,ZO,PS,PB}。 所设计 的 FIS 第 l 条模糊规则如下: Rl:If l ik is A l 1 ,ψik is A l 2 ,l · ik is A l 3 and ψ · ik is A l 4 , then b1 is B l 1 and b2 is B l 2 . 根据式(4),不确定性的逼近值可描述为 d ^ ik(xik,x · ik Θ) = d ^ ik,1(xik,x · ik Θ) d ^ ik,2(xik,x · ik Θ) é ë ê ê ê ù û ú ú ú = Θ T ξ(xik,x · ik) = Θ T 1 ξ(xik,x · ik) Θ T 2 ξ(xik,x · ik) é ë ê ê ê ù û ú ú ú (7) 式中:参数矩阵 Θ∈R 625×2 ,ξ(xik,x · ik)∈R 625×1 。 设 Θ 存在最优参数矩阵 Θ ∗ ,且 Θ ∗满足 Θ ∗ = argmin Θ∈χ 0 sup‖d ^ ik(xik,x · ik Θ) - dik(xik,x · [ ik,t)‖] (8) 式中:χ 0 为包含 Θ 的有界集合。 定义逼近误差的最小值向量为 ρ = d ^ ik(xik,x · ik Θ ∗ ) - dik(xik,x · ik,t) (9) 式中:ρ = [ρ1 ρ2 ] T∈R 2×1 。 针对多机器人编队设计的 FIS 是一个 4 输入 2 输出系统,输入变量具有 5 个模糊子集,所以 FIS 的 规则库有 54 条模糊规则,即 M= 625。 2.2 滑模控制器的设计 定义滑模面 sik(t) = x · eik + λxeik (10) 式中:sik(t)= [sik,1(t) sik,2(t)] T∈R 2×1 ,xeik = xik -xdik∈ R 2×1为跟踪误差向量,xdik为期望轨迹向量,λ 为一个 2×2 的正定矩阵。 定义参考向量 δ(t) = x · dik(t) - λxeik(t) (11) 设计滑模控制律 uk = - Gik[d ^ ik(xik,x · ik Θ) - δ · + κsik + ηsign(sik)] (12) 式中:κ 和 η 均为 2×2 的对角矩阵,即 κ = diag(κ1 , κ2 ),η= diag(η1 ,η2 ),其中 κ1 、κ2 、η1 和 η2 为设计参 数;sign(sik)= [sign(sik,1 ) sign( sik,2 )] T ,sign(·)为 符号函数。 2.3 稳定性证明 定理 1 对于机器人编队系统式(5),设计模糊 补偿器式(7)和滑模控制律式(12)。 如定义参数自 适应律为 Θ · q = Γ -1 q sik,qξ(xik,x · ik) (13) 式中:Γq>0∈R 1 ,κq>0,ηq> | ρq | (q = 1,2),那么多机 器人编队控制系统式(5)是渐近稳定的。 证明 选取李雅普诺夫函数: V(t) = 1 2 (s T ik sik + ∑ 2 q = 1 Θ ~ T qΓqΘ ~ q) (14) 式中:Θ ~ q = Θ ∗ q -Θq,Θ ∗ q 代表最优参数矩阵 Θ ∗ 的第 q 列向量。 对式(14)求一阶导可得 V · (t) = s T ik s · ik + ∑ 2 q = 1 Θ ~ T qΓqΘ ~ q (15) 由式(10)和式(11)可知 s · ik = x¨ ik - δ · (16) 将式(3)和式(16)依次代入式(15)可得 第 5 期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·643·

·644. 智能系统学报 第11卷 V(t)=s[G4u+d4(xt,x4,t)-6]+】 -T/2、-/4、0、/4、π/2;自适应律参数T,=T2= 0.00005:此外入=diag(2.3,2),k=diag(5,15),7= (17) diag(0.5,0.5)。 将式(9)和式(12)代入式(17)可得 仿真实验的给定编队任务,3个机器人从初始位 V(t)=-s[d4(xk,x|⊙)+p-d4(x,x4l⊙°)+ 置,先完成直线编队,然后保持队形跟踪圆形轨迹。 初始位置设置为T,=[0.5m0m/2rad],T2= Kk+sign(sa)]+∑0r,⑥,= [0.8m-0.4m0ad]',x=[1m-0.5mTad]'。领 -s[p +ksa +msign(sa)- 航者跟踪圆形轨迹的线速度=0.5m/s,角速度 w=1rad/s。领航者与2个跟随者期望距离和相角 5(x4)】+∑or,⑧,= 分别为x2=[013mπ/2ad]',x=[0.26mT/2ad]'。 g=1 -sup saksa -sinsign(sa)+ 编队效果如图4所示,图中的实心圆点表示初始位 置,空心圆点表示动态过程中的位置。 豆[8r0+o】 1.0 0.8 0 0- (18) 0.6 00 跟随者3 将参数自适应律式(13)代入式(18)可得 0.4 03 ,跟随者2 V(t)=-sap -saksa -sansign(sa)(19) ① 09 0 一领航者1 考虑nm>lp,I,将其代入式(19)可得 -0.2 000 P0o90 -0.4 V(t)≤-skst<0 (20) ● ● -0.6 0 因此,基于滑模和模糊补偿器的编队控制系统 -0.8 0 具有渐近稳定性。 -1.0 -0.5 0 0.5 1.0 1.5 3仿真结果 x/m 图4直线编队跟踪圆形轨迹 根据上文设计的控制器进行仿真实验,验证该 Fig.4 Line formation while moving in a circle 方法的有效性。采用模糊补偿器和滑模控制器的控 采用文「12]中一阶滑模控制方法和二阶滑模 制方法结构图如图3所示。 控制方法与本文所提出模糊补偿器与滑模控制器相 控制器 结合的控制方法进行对比实验,仿真结果如图5~8 所示。从图5看出,在不确定性上界未知的假设条 佰适应律式(13) FIS 逼近值式(7) 件下,带模糊补偿器的滑模控制方法可以使3个机 xx-xo d(xx) 器人迅速地收敛到期望队形,并以较高的跟踪精度 ò控制律式2) 编队模型式(3) 保持期望队形运动:滑模控制方法的动态响应时间 跟随者k 较长,且由于不确定性的影响在编队形成后存在明 显波动。 图3控制方法结构图 Fig.3 Structure of control scheme 滑模控制的不连续性导致了控制器输出存在抖 设圆形机器人的半径r=0.05m:选择15%的参 振现象,如图6和图7,用饱和函数替换式(12)中的 数波动△,=△:=diag(rand,rand),式中rand表示一 符号函数可以改善这种现象。从图8看出,当编队 个在闭区间[-0.15,0.15]上均匀分布的随机数;考 系统进入滑动模态后,由于不确定性的影响会使系 虑如下周期性外部扰动T.=T,=πa=0.5sin(2mt); 统在滑模面附近产生抖动,但此时L和山已进入平 T =Tby=TKo=0.2sin(mt)o 衡点邻域内,故系统保持局部渐近稳定。由图9可 设领航者i=1,跟随者k=2、3。选取控制器参 知,模糊补偿器可以有效地跟踪编队系统的未知的 数:高斯型隶属函数方差σ,=√2π/8,均值c,取不确定项
V · (t) = s T ik[Gikuk + dik(xik,x · ik,t) - δ · ] + ∑ 2 q = 1 Θ ~ T qΓqΘ ·~ q (17) 将式(9)和式(12)代入式(17)可得 V · (t) = - s T ik[d ^ ik(xik,x · ik Θ) + ρ - d ^ ik(xik,x · ik Θ ∗ ) + κsik + ηsign(sik)] + ∑ 2 q = 1 Θ ~ T qΓqΘ ~ q = - s T ik[ρ + κsik + ηsign(sik) - Θ ~ T ξ(xik,x · ik)] + ∑ 2 q = 1 Θ ~ T qΓqΘ ~ q = - s T ikρ - s T ikκsik - s T ikηsign(sik) + ∑ 2 q = 1 [Θ ~ T qΓqΘ ~ q + Θ ~ T q s T ikξ(xik,x · ik)] (18) 将参数自适应律式(13)代入式(18)可得 V · (t) = - s T ikρ - s T ikκsik - s T ikηsign(sik) (19) 考虑 ηq> | ρq | ,将其代入式(19)可得 V · (t) ≤- s T ikκsik < 0 (20) 因此,基于滑模和模糊补偿器的编队控制系统 具有渐近稳定性。 3 仿真结果 根据上文设计的控制器进行仿真实验,验证该 方法的有效性。 采用模糊补偿器和滑模控制器的控 制方法结构图如图 3 所示。 图 3 控制方法结构图 Fig.3 Structure of control scheme 设圆形机器人的半径 r = 0.05 m;选择 15%的参 数波动 Δi = Δk = diag(rand,rand),式中 rand 表示一 个在闭区间[ -0.15,0.15]上均匀分布的随机数;考 虑如下周期性外部扰动 πix =πiy =πiθ = 0.5sin(2πt); πkx =πky =πkθ = 0.2sin(πt)。 设领航者 i = 1,跟随者 k = 2、3。 选取控制器参 数:高斯型隶属函数方差 σn = 2 π/ 8,均值 cn 取 -π/ 2、-π/ 4、0、π/ 4、π/ 2;自适应律参数 Γ1 = Γ2 = 0.000 05;此外 λ= diag(2.3,2),κ = diag(5,15),η = diag (0.5, 0.5)。 仿真实验的给定编队任务,3 个机器人从初始位 置,先完成直线编队,然后保持队形跟踪圆形轨迹。 初始位置设置为 τ1 = [0.5 m 0m π/ 2 rad] T ,τ2 = [0.8 m -0.4m 0 rad] T ,τ3 =[1 m -0.5 m π rad] T 。 领 航者跟踪圆形轨迹的线速度 v d 1 = 0. 5 m / s,角速度 w d 1 = 1 rad / s。 领航者与 2 个跟随者期望距离和相角 分别为 x 12 d =[0.13 m π/ 2rad] T ,x 13 d =[0.26 m π/ 2rad] T 。 编队效果如图 4 所示,图中的实心圆点表示初始位 置,空心圆点表示动态过程中的位置。 图 4 直线编队跟踪圆形轨迹 Fig.4 Line formation while moving in a circle 采用文[12] 中一阶滑模控制方法和二阶滑模 控制方法与本文所提出模糊补偿器与滑模控制器相 结合的控制方法进行对比实验,仿真结果如图 5 ~ 8 所示。 从图 5 看出,在不确定性上界未知的假设条 件下,带模糊补偿器的滑模控制方法可以使 3 个机 器人迅速地收敛到期望队形,并以较高的跟踪精度 保持期望队形运动;滑模控制方法的动态响应时间 较长,且由于不确定性的影响在编队形成后存在明 显波动。 滑模控制的不连续性导致了控制器输出存在抖 振现象,如图 6 和图 7,用饱和函数替换式(12)中的 符号函数可以改善这种现象。 从图 8 看出,当编队 系统进入滑动模态后,由于不确定性的影响会使系 统在滑模面附近产生抖动,但此时 l ik和 ψik已进入平 衡点邻域内,故系统保持局部渐近稳定。 由图 9 可 知,模糊补偿器可以有效地跟踪编队系统的未知的 不确定项。 ·644· 智 能 系 统 学 报 第 11 卷
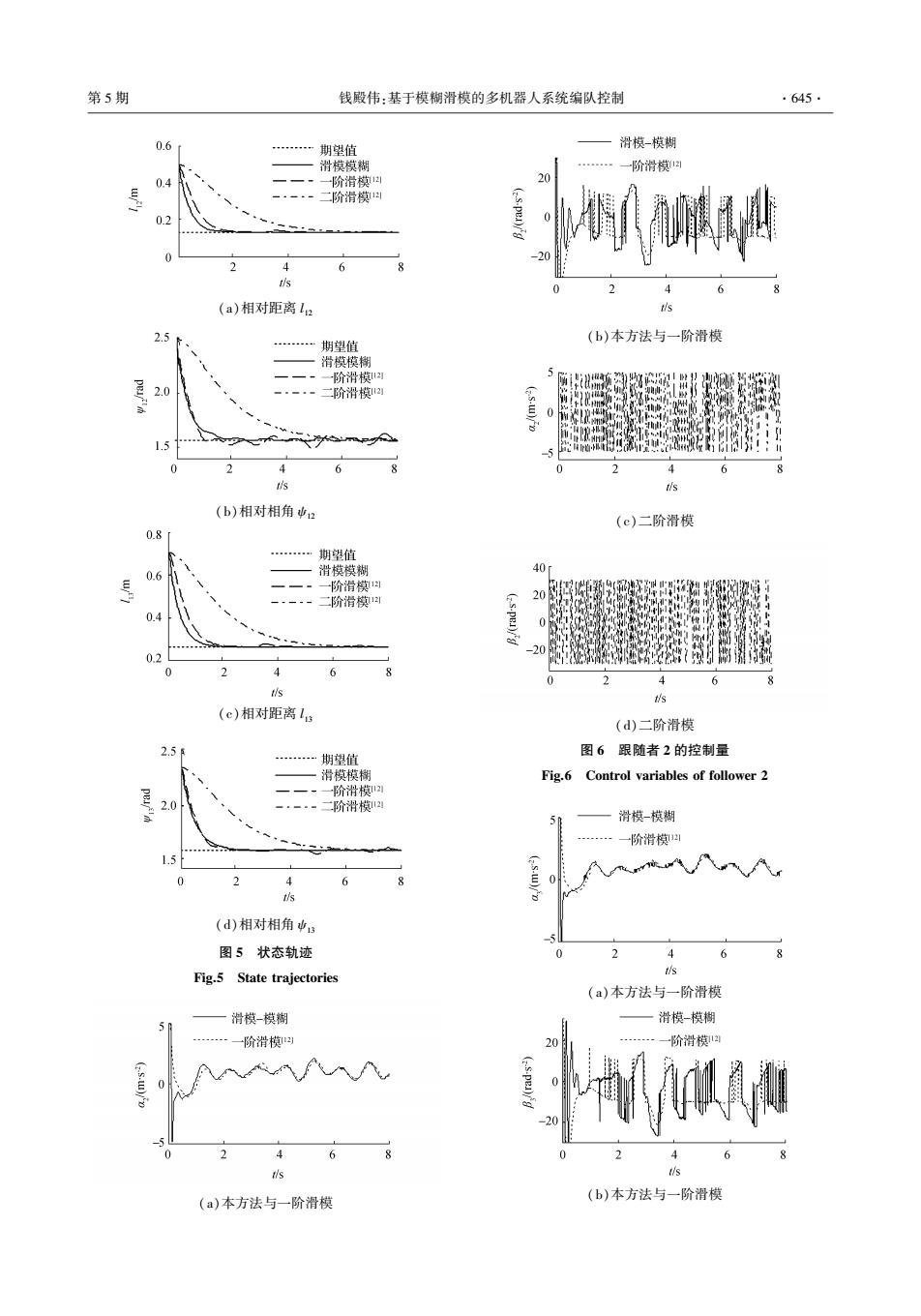
第5期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·645· 0.6 ”期望值 滑模-模糊 滑模模糊 …一阶滑模以 一阶滑模 二阶滑模叫 0.2 型 20 2 4 (a)相对距离le s 2.5 (b)本方法与一阶滑模 …期望值 滑模模糊 一阶滑模2 pe 2.0 二阶滑模2 GA. 0 1.5 2 4 6 2 tis (b)相对相角中2 (c)二阶滑模 0.8 期望值 0.6 滑模模糊 40 一阶滑模1创 阶滑模 20 0.4 -20 0.2 0 2 4 6 0 2 4 s (c)相对距离s (d)二阶滑模 2.5f 图6跟随者2的控制量 ……期望值 滑模模糊 Fig.6 Control variables of follower 2 一·一阶滑模 2.0 一·一·一二阶滑模2四 滑模模糊 阶滑模以 1.5 0 2 4 6 8 s (d)相对相角中3 图5状态轨迹 Fig.5 State trajectories (a)本方法与一阶滑模 5 滑模-模糊 滑模-模糊 阶滑模四 阶滑模凶 20 s (a)本方法与一阶滑模 (b)本方法与一阶滑模
(a)相对距离 l 12 (b)相对相角 ψ12 (c)相对距离 l 13 (d)相对相角 ψ13 图 5 状态轨迹 Fig.5 State trajectories (a)本方法与一阶滑模 (b)本方法与一阶滑模 (c)二阶滑模 (d)二阶滑模 图 6 跟随者 2 的控制量 Fig.6 Control variables of follower 2 (a)本方法与一阶滑模 (b)本方法与一阶滑模 第 5 期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·645·
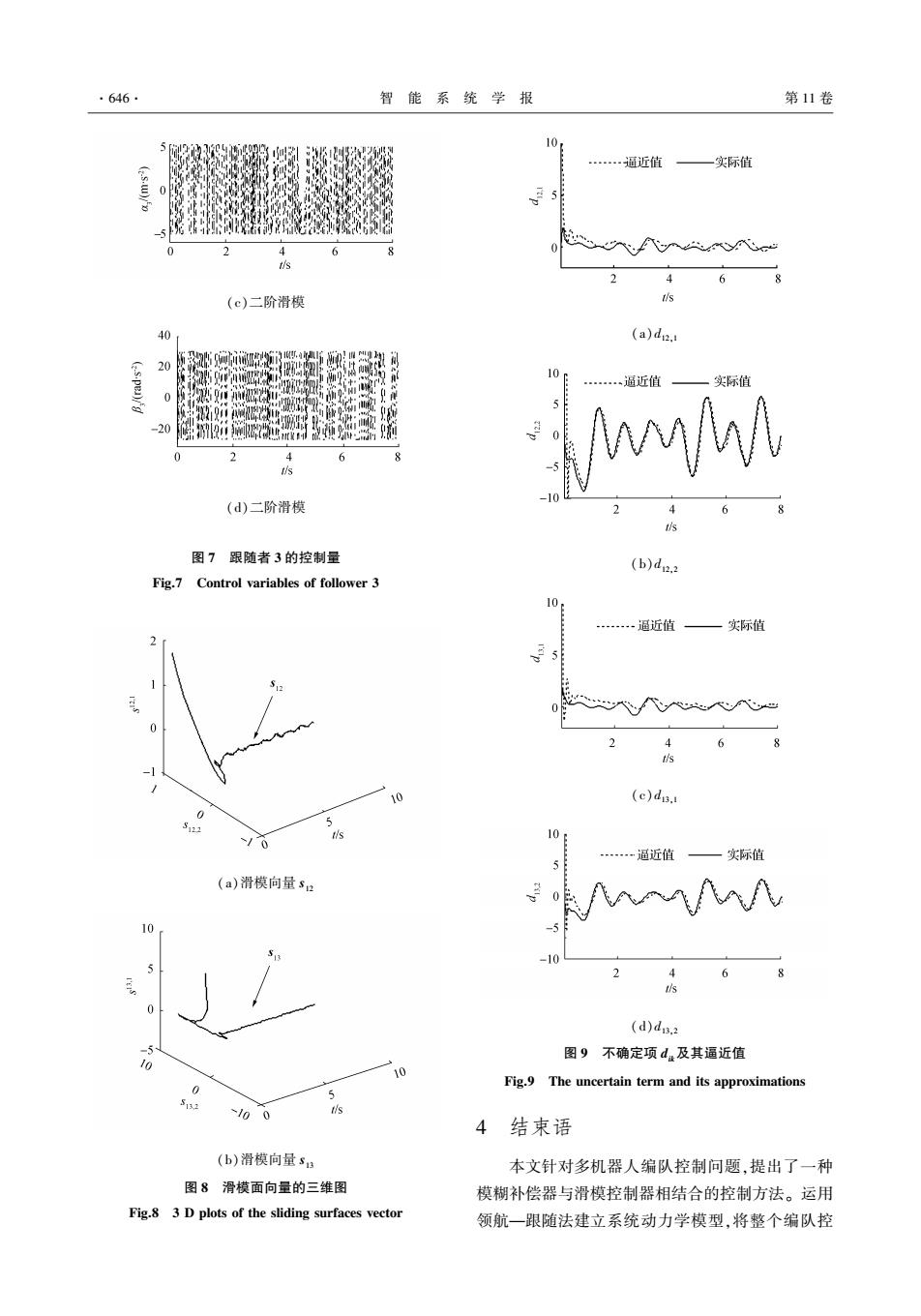
·646. 智能系统学报 第11卷 10 …逼近值 一实际值 5 2 4 4 (c)二阶滑模 s 40 (a)d. 20 (s.pe)/'g -20 2 4 6 s ·nn 通近值 (d)二阶滑模 图7跟随者3的控制量 (b)d22 Fig.7 Control variables of follower 3 10 ……-逼近值 一实际值 5 0 0 2 4 6 10 (c)dn. 5 -10 …一逼近值 一实际值 5 (a)滑模向量s2 (d)d.2 10 图9不确定项d,及其逼近值 Fig.9 The uncertain term and its approximations 5 513 100 s 4 结束语 (b)滑模向量s3 本文针对多机器人编队控制问题,提出了一种 图8滑模面向量的三维图 模糊补偿器与滑模控制器相结合的控制方法。运用 Fig.8 3 D plots of the sliding surfaces vector 领航一跟随法建立系统动力学模型,将整个编队控
(c)二阶滑模 (d)二阶滑模 图 7 跟随者 3 的控制量 Fig.7 Control variables of follower 3 (a)滑模向量 s12 (b)滑模向量 s13 图 8 滑模面向量的三维图 Fig.8 3 D plots of the sliding surfaces vector (a)d12,1 (b)d12,2 (c)d13,1 (d)d13,2 图 9 不确定项 dik及其逼近值 Fig.9 The uncertain term and its approximations 4 结束语 本文针对多机器人编队控制问题,提出了一种 模糊补偿器与滑模控制器相结合的控制方法。 运用 领航—跟随法建立系统动力学模型,将整个编队控 ·646· 智 能 系 统 学 报 第 11 卷

第5期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·647. 制问题转化为若干跟随者的轨迹跟踪问题。利用模 [7]GUILLET A,LENAIN R,THUILOT B,et al.Adaptable 糊逻辑和滑模控制方法对跟随者设计模糊补偿器和 robot formation control:adaptive and predictive formation 滑模控制器,并证明系统的稳定性。仿真结果与滑 control of autonomous vehicles[].IEEE robotics auto- 模编队控制方法进行对比,验证了本文所提出的控 mation magazine,2014,21(1):28-39. 制方法可以有效的克服未知上界的不确定性对编队 [8]LIU Hui,LI Junfeng.Terminal sliding mode control for spacecraft formation flying[.IEEE transactions on aero- 系统的影响:实现多机器人编队在期望队形下对指 space and electronic systems,2009,45(3):835-846. 定轨迹的跟踪。 [9]QIAN Dianwei,TONG Shiwen,GUO Jinrong,et al.Lead- 参考文献: er-follower-based formation control of nonholonomic mobile robots with mismatched uncertainties via integral sliding [1]HUDA M N,YU Hongnian,CANG Shuang.Behaviour- mode[J].Proceedings of the institution of mechanical engi- based control approach for the trajectory tracking of an un- neers,part I:journal of systems and control engineering, deractuated planar capsule robot[J].IET control theory 2015,229(6):559-569. applications,2015,9(2):163-175. [10]袁嫒,焦继乐,曹志强,等.基于模糊控制协调策略的 [2]SADOWSKA A,VAN DEN BROEK T,HUIJBERTS H,et 多自主机器人围捕[J].华中科技大学学报:自然科学 al.A virtual structure approach to formation control of unicy- 版.2011,39(S2):328-331. cle mobile robots using mutual coupling[J].International YUAN Yuan,JIAO Jile,CAO Zhigiang,et al.Fuzzy con- journal of control,2011,84(11)1886-1902. trol coordination based hunting of multiple autonomous ro- [3]杨丽,曹志强,谭民.不确定环境下多机器人的动态编 bots J].Journal of Huazhong university of science and 队控制[J].机器人,2010,32(2):283-288 technology:natural science edition,2011,39(S2):328- YANG Li,CAO Zhiqiang,TAN Min.Dynamic formation 331. control for multiple robots in uncertain environments[J ] [11]王雪松,高阳,程玉虎,等.知识引导遗传算法实现机 Robot,2010,32(2):283-288. 器人路径规划[J].控制与决策,2009,24(7):1043- [4]WANG Jinliang,WU Huaining.Leader-following formation 1049. control of multi-agent systems under fixed and switching to- WANG Xuesong,GAO Yang,CHENG Yuhu,et al. pologies[]]International journal of control,2012,85(6): Knowledge-guided genetic algorithm for path planning of 695-705. robot[J].Control and decision,2009,24(7):1043- [5]王奎民,赵玉飞,侯恕萍,等.一种改进人工势场的 1049 UUV动碍航物规避方法[J].智能系统学报,2014,9 [12]DEFOORT M,FLOQUET T,KOKOSY A,et al.Sliding- (1):47-52 mode formation control for cooperative autonomous mobile WANG Kuimin,ZHAO Yufei,HOU Shuping,et al.Dy- robots[J].IEEE transactions on industrial electronics, namic obstacle avoidance for unmanned underwater vehicle 2008,55(11):3944-3953. based on an improved artificial potential field [J].CAAl 作者简介: transactions on intelligent systems,2014,9(1):47-52. 钱殿伟,男,1980年生,副教授,博 [6]ZHAO Weihua,GO T H.Quadcopter formation flight control 士,主要研究方向为变结构控制理论与 combining MPC and robust feedback linearization[J].Jour- 应用、智能机器人技术、欠驱动机器人 nal of the franklin institute,2014,351(3):1335-1355. 控制
制问题转化为若干跟随者的轨迹跟踪问题。 利用模 糊逻辑和滑模控制方法对跟随者设计模糊补偿器和 滑模控制器,并证明系统的稳定性。 仿真结果与滑 模编队控制方法进行对比,验证了本文所提出的控 制方法可以有效的克服未知上界的不确定性对编队 系统的影响;实现多机器人编队在期望队形下对指 定轨迹的跟踪。 参考文献: [ 1] HUDA M N, YU Hongnian, CANG Shuang. Behaviour⁃ based control approach for the trajectory tracking of an un⁃ deractuated planar capsule robot[ J]. IET control theory & applications, 2015, 9(2): 163⁃175. [2]SADOWSKA A, VAN DEN BROEK T, HUIJBERTS H, et al. A virtual structure approach to formation control of unicy⁃ cle mobile robots using mutual coupling [ J]. International journal of control, 2011, 84(11): 1886⁃1902. [3]杨丽, 曹志强, 谭民. 不确定环境下多机器人的动态编 队控制[J]. 机器人, 2010, 32(2): 283⁃288. YANG Li, CAO Zhiqiang, TAN Min. Dynamic formation control for multiple robots in uncertain environments [ J]. Robot, 2010, 32(2): 283⁃288. [4]WANG Jinliang, WU Huaining. Leader⁃following formation control of multi⁃agent systems under fixed and switching to⁃ pologies[J]. International journal of control, 2012, 85(6): 695⁃705. [5]王奎民, 赵玉飞, 侯恕萍, 等. 一种改进人工势场的 UUV 动碍航物规避方法[ J]. 智能系统学报, 2014, 9 (1): 47⁃52. WANG Kuimin, ZHAO Yufei, HOU Shuping, et al. Dy⁃ namic obstacle avoidance for unmanned underwater vehicle based on an improved artificial potential field [ J]. CAAI transactions on intelligent systems, 2014, 9(1): 47⁃52. [6]ZHAO Weihua, GO T H. Quadcopter formation flight control combining MPC and robust feedback linearization[J]. Jour⁃ nal of the franklin institute, 2014, 351(3): 1335⁃1355. [7]GUILLET A, LENAIN R, THUILOT B, et al. Adaptable robot formation control: adaptive and predictive formation control of autonomous vehicles[ J]. IEEE robotics & auto⁃ mation magazine, 2014, 21(1): 28⁃39. [8] LIU Hui, LI Junfeng. Terminal sliding mode control for spacecraft formation flying[ J]. IEEE transactions on aero⁃ space and electronic systems, 2009, 45(3): 835⁃846. [9]QIAN Dianwei, TONG Shiwen, GUO Jinrong, et al. Lead⁃ er⁃follower⁃based formation control of nonholonomic mobile robots with mismatched uncertainties via integral sliding mode[J]. Proceedings of the institution of mechanical engi⁃ neers, part I: journal of systems and control engineering, 2015, 229(6): 559⁃569. [10]袁媛, 焦继乐, 曹志强, 等. 基于模糊控制协调策略的 多自主机器人围捕[J]. 华中科技大学学报: 自然科学 版, 2011, 39(S2): 328⁃331. YUAN Yuan, JIAO Jile, CAO Zhiqiang, et al. Fuzzy con⁃ trol coordination based hunting of multiple autonomous ro⁃ bots [ J]. Journal of Huazhong university of science and technology: natural science edition, 2011, 39( S2): 328⁃ 331. [11]王雪松, 高阳, 程玉虎, 等. 知识引导遗传算法实现机 器人路径规划[ J]. 控制与决策, 2009, 24( 7): 1043⁃ 1049. WANG Xuesong, GAO Yang, CHENG Yuhu, et al. Knowledge⁃guided genetic algorithm for path planning of robot[ J]. Control and decision, 2009, 24 ( 7): 1043⁃ 1049. [12]DEFOORT M, FLOQUET T, KOKOSY A, et al. Sliding⁃ mode formation control for cooperative autonomous mobile robots [ J ]. IEEE transactions on industrial electronics, 2008, 55(11): 3944⁃3953. 作者简介: 钱殿伟,男,1980 年生,副教授,博 士,主要研究方向为变结构控制理论与 应用、智能机器人技术、欠驱动机器人 控制。 第 5 期 钱殿伟:基于模糊滑模的多机器人系统编队控制 ·647·