
第10卷第6期 智能系统学报 Vol.10 No.6 2015年12月 CAAI Transactions on Intelligent Systems Dee.2015 D0L:10.11992/is.201504027 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20151111.1633.006.html 基于最大间隔理论的组合距离学习算法 郭瑛洁,王士同,许小龙 (江南大学数字媒体学院,江苏无锡214000) 摘要:从已知数据集中学习距离度量在许多机器学习应用中都起着重要作用。传统的距离学习方法通常假定目 标距离函数为马氏距离的形式,这使得学习出的距离度量在应用上具有局限性。提出了一种新的距离学习方法,将 目标距离函数表示为若干候选距离的线性组合,依据最大间隔理论利用数据集的边信息学习得到组合距离中各距 离分量的权值,从而得到新的距离度量。通过该距离度量在模糊C均值聚类算法中的表现来对其进行评价。在UCI 数据集上,与其他已有的距离学习算法的对比实验结果证明了该文算法的有效性。 关键词:距离学习:组合距离:最大间隔:F℃M:模糊聚类;聚类算法;距离:学习算法 中图分类号:TP181文献标志码:A文章编号:1673-4785(2015)06-0843-08 中文引用格式:郭瑛洁,王士同,许小龙.基于最大间隔理论的组合距离学习算法[J].智能系统学报,2015,10(6):843-850. 英文引用格式:GUO Yingjie,WANG Shitong,XU Xiaolong.Learning a linear combination of distances based on the maximum: margin theory[J].CAAI Transactions on Intelligent Systems,2015,10(6):843-850. Learning a linear combination of distances based on the maximum-margin theory GUO Yingjie,WANG Shitong,XU Xiaolong (School of Digital Media,Jiangnan University,Wuxi 214000,China) Abstract:Learning a distance metric from given training samples is a crucial aspect of many machine learning tasks. Conventional distance metric learning approaches often assume the target distance function to be represented in the form of Mahalanobis distance,and the metric has limitations for this application.This paper proposes a new metric learning approach in which the target distance function is represented as a linear combination of several candidate distance metrics.This method obtains a new distance metric by learning weights from side information according to the maximum-margin theory.The new distance function is applied to fuzzy C-means clustering for evaluation.The experiments were performed using UCI data,and a comparison of the results with those of other approaches reveals the advantages of the proposed technique. Keywords:metric learning;hybrid distance metric;maximum-margin theory;fuzzy C-means;fuzzy clustering; clustering algorithm;metric;learning algorithm 如何表示2点之间的距离是模式识别中的基础 特征空间中超球结构的数据集,对于超立方体结构、 问题。一个好的距离度量能够根据数据的结构与分 超椭球结构的数据集效果不太理想四。除了欧氏 布适用于不同的应用。欧氏距离是众多数据挖掘应 距离,余弦距离是另一个应用广泛的距离度量。尽 用中使用最多的距离度量,但是欧氏距离仅适用于 管余弦距离在文本检索中有优秀的表现,但是其预 先假设了数据集每一维度都是等权重的[☒】,这一特 收稿日期:2015-04-19.网络出版日期:2015-11-11. 性显然限制了余弦距离的应用范围。因此,欧式距 基金项目:国家自然科学基金资助项目(61272210):江苏省自然科学基 金资助项目(BK2011417,BK2011003). 离和余弦距离在实际应用中都不是最理想的选择。 通信作者:郭瑛洁.E-mail:ying_dm@163.com. 从训练样本中学习出合适的距离度量是近年来
第 10 卷第 6 期 智 能 系 统 学 报 Vol.10 №.6 2015 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2015 DOI:10.11992 / tis.201504027 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20151111.1633.006.html 基于最大间隔理论的组合距离学习算法 郭瑛洁,王士同,许小龙 (江南大学 数字媒体学院 ,江苏 无锡 214000) 摘 要:从已知数据集中学习距离度量在许多机器学习应用中都起着重要作用。 传统的距离学习方法通常假定目 标距离函数为马氏距离的形式,这使得学习出的距离度量在应用上具有局限性。 提出了一种新的距离学习方法,将 目标距离函数表示为若干候选距离的线性组合,依据最大间隔理论利用数据集的边信息学习得到组合距离中各距 离分量的权值,从而得到新的距离度量。 通过该距离度量在模糊 C 均值聚类算法中的表现来对其进行评价。 在 UCI 数据集上,与其他已有的距离学习算法的对比实验结果证明了该文算法的有效性。 关键词:距离学习;组合距离;最大间隔;FCM;模糊聚类;聚类算法;距离;学习算法 中图分类号:TP181 文献标志码:A 文章编号:1673⁃4785(2015)06⁃0843⁃08 中文引用格式:郭瑛洁,王士同,许小龙. 基于最大间隔理论的组合距离学习算法[J]. 智能系统学报, 2015, 10(6): 843⁃850. 英文引用格式:GUO Yingjie, WANG Shitong, XU Xiaolong. Learning a linear combination of distances based on the maximum⁃ margin theory[J]. CAAI Transactions on Intelligent Systems, 2015, 10(6): 843⁃850. Learning a linear combination of distances based on the maximum⁃margin theory GUO Yingjie, WANG Shitong, XU Xiaolong (School of Digital Media, Jiangnan University, Wuxi 214000, China) Abstract:Learning a distance metric from given training samples is a crucial aspect of many machine learning tasks. Conventional distance metric learning approaches often assume the target distance function to be represented in the form of Mahalanobis distance, and the metric has limitations for this application. This paper proposes a new metric learning approach in which the target distance function is represented as a linear combination of several candidate distance metrics. This method obtains a new distance metric by learning weights from side information according to the maximum⁃margin theory. The new distance function is applied to fuzzy C⁃means clustering for evaluation. The experiments were performed using UCI data, and a comparison of the results with those of other approaches reveals the advantages of the proposed technique. Keywords: metric learning; hybrid distance metric; maximum⁃margin theory; fuzzy C⁃means; fuzzy clustering; clustering algorithm; metric; learning algorithm 收稿日期:2015⁃04⁃19. 网络出版日期:2015⁃11⁃11. 基金项目:国家自然科学基金资助项目(61272210);江苏省自然科学基 金资助项目(BK2011417, BK2011003). 通信作者:郭瑛洁. E⁃mail:ying_dm@ 163.com. 如何表示 2 点之间的距离是模式识别中的基础 问题。 一个好的距离度量能够根据数据的结构与分 布适用于不同的应用。 欧氏距离是众多数据挖掘应 用中使用最多的距离度量,但是欧氏距离仅适用于 特征空间中超球结构的数据集,对于超立方体结构、 超椭球结构的数据集效果不太理想[1] 。 除了欧氏 距离,余弦距离是另一个应用广泛的距离度量。 尽 管余弦距离在文本检索中有优秀的表现,但是其预 先假设了数据集每一维度都是等权重的[2] ,这一特 性显然限制了余弦距离的应用范围。 因此,欧式距 离和余弦距离在实际应用中都不是最理想的选择。 从训练样本中学习出合适的距离度量是近年来

·844 智能系统学报 第10卷 的研究热点,它对于提高聚类和分类效果有着重要 的影响。一般的距离学习方法都是首先假定一个距 s..0=1. i=1 离函数模型并进行求解,其中大部分的距离函数假 0≤ω:≤1,i=1,2,…,p 定在马氏距离定义的框架之下,即对于2点x、y,使 式中:D(x。,x6)表示数据点x。到数据点x。之间的 用距离公式d(x,y)=(x-y)A(x-y),其中A为 距离,它由p个距离分量组成,d,(x,x6)是其第i 所要学习的距离矩阵。比如文献[3]中通过使相似 个距离分量,w:是第i个距离分量所对应的权值。 样本之间距离减小学习了一个全局距离度量:区分 ω,需要满足各个分量权值均为正且和为1的条件。 成分分析(DCA)[4)通过最小化相似样本之间距离 在距离分量的选择上,除了经典的欧式距离之 的同时最大化不相似样本之间的距离来学习距离矩 外,本文选择了若干含有数据维度方差的距离分量 阵:近邻成分分析(NCA)[)通过最优化最近邻分类 (如:dxx)=(x。-x)'乙(x-x),其中B 器的精度去学习马氏距离度量:最大边界近邻分类 Bo 方法(LMNN)[在NCA的框架下拓展了最大边界 为常数,I为单位矩阵,σ为数据点之间的标准差) 的目标,但是学习的目标仍然是得到一个马氏距离。 以保留数据各特征分量上的特征。但是这些距离均 当马氏距离中的矩阵A取单位矩阵I时,则马氏距 为马氏距离定义框架下的距离度量,对其进行线性 离表示欧氏距离。因此,本质上来说,以马氏距离为 组合后,得到的距离函数仍为马氏距离形式。因此 目标学习得到的新距离是欧式距离的线性变换,其 根据Wu等提出的新距离8】,本文给出了若干形如 无法准确地度量所有样本之间的距离。 d(x。,x。)=1-exp(-B‖x.-x‖2)的距离分量 有别于传统的距离学习方法,本文提出的距离 进行组合,其中B为常数,这些距离均为非线性的距 学习方法并没有将学习目标单纯设定为马氏距离, 离度量,通过组合可以形成非线性的距离函数以克 而是学习由若干候选距离线性组合而成的新距离。 服马氏距离的缺点。 基于最大间隔理论建立目标函数,利用数据的边信 2基于最大间隔理论的距离学习 息通过对目标函数进行优化从而得到组合距离中的 权重进而得到新的距离度量。对于候选距离的选择 2.1距离学习方法 也不仅仅局限于马氏距离,本文选择了其他形式的 本文所提出的距离学习算法将利用数据集的边 距离度量进行组合,以扩大距离度量的适用范围。 信息进行学习,而边信息通常以成对约束的形式表 现。因此,本文以成对约束的集合作为训练集并表 1 组合距离表示 示为D={(x,x,y),k=1,2,…,n},其中n为成 为了更好地表示数据点之间的距离,在距离函 对约束的对数。D中每一对成对约束(x,x,y)都 数中引入权重来强化有积极作用的部分,削减冗余 是一个包含三个元素的元组,其中x和x是被表示 的部分,已经成为一种常用的方法。在之前的方法 为d维向量的样本点,y是表示样本点x和x之间 中,研究者往往使用特征加权距离的方法)来改进 关系的类标。当x和x为同一类的样本点时,y 聚类算法,特征加权距离的计算表达式为 为正(如:y=+1);反之,y为负(如:yk=-1)。 使用X=(x1,x2,…,xx)来表示D中出现的所有的 0(x,y)= ∑(-y4)2,a>1 训练样本点,其中N表示样本点的个数。 h= 式中: 统计学习中常用的经验风险最小化并不能保证 [x1x2… xalT,y [y2·y]T为特征空间R中的任意2点, 良好的泛化性能,因此间隔理论[9]就伴随着过拟合 的问题研究被提出,并逐渐成为机器学习领域中的 仙,为特征权重且满足0,=1。 一个重要评价标准。本文依据最大间隔理论并受 h=1 受特征加权距离的启发,引入权值将距离函数 L2-SVM方法[o]和文献[2]的启发,构建目标函数 改写为若干候选距离的线性组合,将特征加权改为 如式(2): 距离加权,从而强化对某一数据集有更好度量效果 min/= +c +B2-p 的距离分量。 21 k=1 本文通过以下线性组合来表示数据集中的距离 t(∑u,d(xx)-B)≥p- (2) 度量: D(xa,6)= (1) 20=10≤a≤1i=1,2p 三1
的研究热点,它对于提高聚类和分类效果有着重要 的影响。 一般的距离学习方法都是首先假定一个距 离函数模型并进行求解,其中大部分的距离函数假 定在马氏距离定义的框架之下,即对于 2 点 x、y ,使 用距离公式 d(x,y) = (x - y) TA(x - y) ,其中 A 为 所要学习的距离矩阵。 比如文献[3]中通过使相似 样本之间距离减小学习了一个全局距离度量;区分 成分分析(DCA) [4] 通过最小化相似样本之间距离 的同时最大化不相似样本之间的距离来学习距离矩 阵;近邻成分分析(NCA) [5] 通过最优化最近邻分类 器的精度去学习马氏距离度量;最大边界近邻分类 方法(LMNN) [6] 在 NCA 的框架下拓展了最大边界 的目标,但是学习的目标仍然是得到一个马氏距离。 当马氏距离中的矩阵 A 取单位矩阵 I 时,则马氏距 离表示欧氏距离。 因此,本质上来说,以马氏距离为 目标学习得到的新距离是欧式距离的线性变换,其 无法准确地度量所有样本之间的距离。 有别于传统的距离学习方法,本文提出的距离 学习方法并没有将学习目标单纯设定为马氏距离, 而是学习由若干候选距离线性组合而成的新距离。 基于最大间隔理论建立目标函数,利用数据的边信 息通过对目标函数进行优化从而得到组合距离中的 权重进而得到新的距离度量。 对于候选距离的选择 也不仅仅局限于马氏距离,本文选择了其他形式的 距离度量进行组合,以扩大距离度量的适用范围。 1 组合距离表示 为了更好地表示数据点之间的距离,在距离函 数中引入权重来强化有积极作用的部分,削减冗余 的部分,已经成为一种常用的方法。 在之前的方法 中,研究者往往使用特征加权距离的方法[7] 来改进 聚类算法,特征加权距离的计算表达式为 wdist(x,y) = ∑ d h = 1 ω α h (xh - yh ) 2 ,α > 1 式 中: x = x1 x2 … xd [ ] T ,y = y1 y2 … y [ d ] T 为特征空间 R d 中的任意 2 点, ωh 为特征权重且满足 ∑ d h = 1 ωh =1。 受特征加权距离的启发,引入权值将距离函数 改写为若干候选距离的线性组合,将特征加权改为 距离加权,从而强化对某一数据集有更好度量效果 的距离分量。 本文通过以下线性组合来表示数据集中的距离 度量: D(xa ,xb) = ∑ p i = 1 ωidi(xa ,xb) (1) s.t.∑ p i = 1 ωi = 1, 0 ≤ ωi ≤ 1, i = 1,2,…,p 式中: D(xa ,xb) 表示数据点 xa 到数据点 xb 之间的 距离,它由 p 个距离分量组成, di( xa , xb) 是其第 i 个距离分量, ωi 是第 i 个距离分量所对应的权值。 ωi 需要满足各个分量权值均为正且和为 1 的条件。 在距离分量的选择上,除了经典的欧式距离之 外,本文选择了若干含有数据维度方差的距离分量 (如: d(xa ,xb) = (xa - xb) T I βσ 2 (xa - xb) ,其中 β 为常数, I 为单位矩阵, σ 为数据点之间的标准差) 以保留数据各特征分量上的特征。 但是这些距离均 为马氏距离定义框架下的距离度量,对其进行线性 组合后,得到的距离函数仍为马氏距离形式。 因此, 根据 Wu 等提出的新距离[8] ,本文给出了若干形如 d(xa ,xb) = 1 - exp( - β ‖ xa - xb‖2 ) 的距离分量 进行组合,其中 β 为常数,这些距离均为非线性的距 离度量,通过组合可以形成非线性的距离函数以克 服马氏距离的缺点。 2 基于最大间隔理论的距离学习 2.1 距离学习方法 本文所提出的距离学习算法将利用数据集的边 信息进行学习,而边信息通常以成对约束的形式表 现。 因此,本文以成对约束的集合作为训练集并表 示为 D = x k a ,x k b,yk { ( ) ,k = 1,2,…,n} ,其中 n 为成 对约束的对数。 D 中每一对成对约束 x k a ,x k b,yk ( ) 都 是一个包含三个元素的元组,其中 x k a 和 x k b 是被表示 为 d 维向量的样本点, yk 是表示样本点 x k a 和 x k b 之间 关系的类标。 当 x k a 和 x k b 为同一类的样本点时, yk 为正(如: yk = + 1);反之, yk 为负(如: yk = - 1)。 使用 X = x1 ,x2 ,…,xN ( ) 来表示 D 中出现的所有的 训练样本点,其中 N 表示样本点的个数。 统计学习中常用的经验风险最小化并不能保证 良好的泛化性能,因此间隔理论[9 ] 就伴随着过拟合 的问题研究被提出,并逐渐成为机器学习领域中的 一个重要评价标准。 本文依据最大间隔理论并受 L2⁃SVM 方法[10 ]和文献[2] 的启发,构建目标函数 如式(2): minJ = 1 2 ∑ p i = 1 ω 2 i + C∑ n k = 1 ξ 2 k + β 2 - θρ s.t.yk(∑ p i = 1 ωidi(x k a ,x k b) - β) ≥ ρ - ξk ∑ p i = 1 ωi = 1,0 ≤ ωi ≤ 1,i = 1,2,…,p (2) ·844· 智 能 系 统 学 报 第 10 卷

第6期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 ·845· 式中:d,(x,x)表示第k对成对约束的第i个距离 将拉格朗日函数式(5)分别对ω:Bp、专、入求 分量,为了便于表示,本文在后续的介绍中将使用符 偏导,并令其等于0得到 号d来代替d,(x。,x)。此外,y为该约束对的类 aL 标,C为惩罚因子,C值大时对训练错误的惩罚增 =w:- dw, A04A=0 大,0为已知参数,B为阀值,最大间隔为P aL wⅡ =29- ar=0 在优化的过程中最大化p,最小化‖wⅡ2,并使训 aL =-9+∑a4=0 (5) 练误差专.最小化,其中k≥0。 ap =1 本文的目标是通过优化该目标函数求得距离分 aL 量的权值ω:,下面将具体介绍求解ω:的方法。为 a店 =2C吃k-a4=0 了求解上述优化问题,将它作为原始最优化问题,应 用拉格朗日对偶性,通过求解对偶问题得到原始问 1 名=0 题的最优解。接下来将介绍具体求解过程。 进而得到 首先,构建拉格朗日函数如式(3): (6) k=1 =1 B= (7) 26=1 i=1 -名 =∑a4 (8) (3) k=1 Q: 式中:a=【a,a…a,】T、A均为拉格朗日乘子。 5:-2C (9) 如果此时考虑式(2)中ω:≥0的约束条件,并 (10) 将该条件加入拉格朗日函数,则得到 将式(6)代入式(10)得到 L'=L- 名m (11) 将该拉格朗日函数分别对ω:Bp、专:、入求偏 A=-文ad 导,并令其等于0得到 进而,将式(11)代入式(6)得到 aL' =w:- dw. 2d4-A-9,=0 k=1 aL' 将式(7)~(10)、(12)代入拉格朗日函数(3) aβ =2B- a=0 中,即得 k=1 aL' =-0+】 (4) ap 4=0 =1 aL' =2C54-ak=0 (名三ad)P- a店 OL' =1- 2(店42ax4)+ a入 2,=0 i= 显然由方程组(4)无法求得ω:,因此本文先暂 喜,京ax 时不考虑ω:≥0的约束条件,使用式(3)进行后续 即 的求解。 根据拉格朗日对偶性,原始问题的对偶问题是 (w,B,5,a,)=写 B,5 极大极小问题: max minL(w,B,5,a,入) .8,E 所以,需要先求L(w,B,专,x,入)对于ω、入的 极小值
式中: di(x k a ,x k b) 表示第 k 对成对约束的第 i 个距离 分量,为了便于表示,本文在后续的介绍中将使用符 号 di.k 来代替 di(x k a ,x k b) 。 此外, yk 为该约束对的类 标, C 为惩罚因子, C 值大时对训练错误的惩罚增 大, θ 为已知参数, β 为阈值,最大间隔为 ρ ‖ω‖ 。 在优化的过程中最大化 ρ ,最小化 ‖ω‖2 ,并使训 练误差 ξ k 最小化,其中 ξ k ≥ 0。 本文的目标是通过优化该目标函数求得距离分 量的权值 ωi, 下面将具体介绍求解 ωi 的方法。 为 了求解上述优化问题,将它作为原始最优化问题,应 用拉格朗日对偶性,通过求解对偶问题得到原始问 题的最优解。 接下来将介绍具体求解过程。 首先,构建拉格朗日函数如式(3): L = 1 2 ∑ p i = 1 ω 2 i + C∑ n k = 1 ξ 2 k + β 2 - θρ + ∑ n k = 1 αk ρ - ξk - yk ∑ p i = 1 ωidi,k ( ( - β) ) + λ 1 - ∑ p i = 1 ( ωi) (3) 式中:α = α1 α2 … αn [ ] T 、λ 均为拉格朗日乘子。 如果此时考虑式(2)中 ωi ≥ 0 的约束条件,并 将该条件加入拉格朗日函数,则得到 L′ = L - ∑ p i = 1 φiωi 将该拉格朗日函数分别对 ωi、β、ρ、ξ k、λ 求偏 导,并令其等于 0 得到 ∂L′ ∂ωi = ωi - ∑ n k = 1 αk ykdi,k - λ - φi = 0 ∂L′ ∂β = 2β - ∑ n k = 1 αk yk = 0 ∂L′ ∂ρ = - θ + ∑ n k = 1 αk = 0 ∂L′ ∂ξk = 2Cξk - αk = 0 ∂L′ ∂λ = 1 - ∑ p i = 1 ωi = 0 ì î í ï ï ï ï ï ï ï ï ï ï ï ï ï ï (4) 显然由方程组(4)无法求得 ωi ,因此本文先暂 时不考虑 ωi ≥ 0 的约束条件,使用式(3)进行后续 的求解。 根据拉格朗日对偶性,原始问题的对偶问题是 极大极小问题: max α min ω,β,ξ L(ω,β,ξ,α,λ) 所以,需要先求 L(ω,β,ξ,α,λ) 对于 ω、λ 的 极小值。 将拉格朗日函数式(5)分别对 ωi、β、ρ、ξ k、λ 求 偏导,并令其等于 0 得到 ∂L ∂ωi = ωi - ∑ n k = 1 αk ykdi,k - λ = 0 ∂L ∂β = 2β - ∑ n k = 1 αk yk = 0 ∂L ∂ρ = - θ + ∑ n k = 1 αk = 0 ∂L ∂ξk = 2Cξk - αk = 0 ∂L ∂λ = 1 - ∑ p i = 1 ωi = 0 ì î í ï ï ï ï ï ï ï ï ï ï ï ï ï ï (5) 进而得到 ωi = ∑ n k = 1 αk ykdi,k + λ (6) β = 1 2 ∑ n k = 1 αk yk (7) θ = ∑ n k = 1 αk (8) ξk = αk 2C (9) 1 - ∑ p i = 1 ωi = 0 (10) 将式(6)代入式(10)得到 λ = 1 p 1 - ∑ n k = 1 αk y ( kdi,k ) (11) 进而,将式(11)代入式(6)得到 ωi = 1 p - 1 p ∑ p i = 1 ∑ n k = 1 αk ykdi,k + ∑ n k = 1 αk ykdi,k (12) 将式(7) ~ (10)、(12) 代入拉格朗日函数(3) 中,即得 L = 1 2p - 1 p ∑ p i = 1 ∑ n k = 1 αk ykdi,k + 1 2p ∑ p i = 1 ∑ n k = 1 αk y ( kdi,k ) 2 - 1 2 ∑ p i = 1 ∑ n q = 1 αq yqdi,q∑ n r = 1 αr y ( rdi,r) + ∑ n q = 1 αq yq∑ n r = 1 αr yr 即 min ω,β,ξ L(ω,β,ξ,α,λ) = 1 2p - 1 p ∑ p i = 1 ∑ n k = 1 αk ykdi,k + 1 2p ∑ p i = 1 ∑ n k = 1 αk y ( kdi,k ) 2 - 1 2 ∑ p i = 1 ∑ n q = 1 αq yqdi,q∑ n r = 1 αr y ( rdi,r) + 第 6 期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 ·845·

·846. 智能系统学报 第10卷 表示无法使w,取正值的i的集合,2个集合p和p 的大小分别使用lp|和p|来表示。 求minL(w,B,专,a,入)对x的极大,即得对偶问题: B,5 至此完成求解距离分量权值ω:的目标,求解集 合p和pˉ的算法描述将在下一小节给出。 max 2印p台台 最大几何间隔0中的p亦可在求解权值 ω:的过程中求得。与原始SVM类似,目标函数(3) 的分商超平面为名如4。一B)=p.即可得最大 ain=0 函数间隔p=y (∑a,ds一B)。在求得最优解后 立4=0 由式(9)可得B的最优解B·= ay进而可得 ak≥0,k=1,2,…,n (13) 将式(13)的目标函数由求极大转换为求极小, 最大函数同隔p=名如,d。一B产)。 就得到下面与之等价的对偶最优化问题: 2.2算法描述 本节将给出求解距离分量权值ω:的具体算法 步骤。 为了便于表示,将式(14)简化: 0,i E p (15) Ue'I +CV:,i∈p aav-g 式中: 含=0 k=1 由式(16)观察可得,若想满足®,为正值,则V: a4≥0,k=1,2,…,n 需要足够大,且当V:越大,ω:为正值的几率就越大。 如此,可以通过二次规划的求解方法得到最优 因此,求解集合p和p的算法总结如下。 解a·=[a1a…a]T,进而代人式(12)得 算法1求解集合p和p。 到w,的最优解: 1)初始化:P。=☑,P={1,2,…,p,h=0: =-ad+4 pp i=ik=1 2)h=h+1,P=P,+{i计,P%=pP-,-i,其 可以明显地观察到,即使成功的优化得到最优 中,i=arg maxi{V}; 解,也不能保证w:完全满足式(2)中ω:≥0的约束 3)通过式(14)计算w。并判断其是否大于0。 条件,受P℉℃算法[的启发,在之前的基础上对ω, 其中,g=arg min,ex{V}。如果w,>0则回到2), 做如下修改: 否则设置p*=PP=P-1并终止。 下面将介绍学习距离函数中权值ω:的算法,其 0:= 中ω,将采用如下方法初始化:在式(1)中ω:的约束 0,i∈p 条件下,令ω0=ω)=…=ω0,因此有ω0= 1/P。 算法2学习距离函数。 (14) 输入: 式中: 1)数据矩阵:X∈Rw; p={i:w:=0明 2)成对约束:(xy)其中,y={+1,-1: p={i:ω:>0} 3)参数:C、0: p表示所有使得ω:取正值的i的集合,相对应的p 输出:距离权值:ω;
∑ n q = 1 αq yq∑ n r = 1 αr yr 求 min ω,β,ξ L(ω,β,ξ,α,λ) 对 α 的极大,即得对偶问题: max α 1 2p - 1 p ∑ p i = 1 ∑ n k = 1 αk ykdi,k + 1 2p ∑ p i = 1 ∑ n k = 1 αk y ( kdi,k ) 2 - 1 2 ∑ p i = 1 ∑ n q = 1 αq yqdi,q∑ n r = 1 αr y ( rdi,r) + ∑ n q = 1 αq yq∑ n r = 1 αr yr s.t.∑ n k = 1 αk yk = 0 ∑ n k = 1 αk = θ αk ≥ 0,k = 1,2,…,n (13) 将式(13)的目标函数由求极大转换为求极小, 就得到下面与之等价的对偶最优化问题: min α - 1 2p + 1 p ∑ p i = 1 ∑ n k = 1 αk ykdi,k - 1 2p ∑ p i = 1 ∑ n k = 1 αk y ( kdi,k ) 2 + 1 2 ∑ p i = 1 ∑ n q = 1 αq yqdi,q∑ n r = 1 αr y ( rdi,r) - ∑ n q = 1 αq yq∑ n r = 1 αr yr s.t.∑ n k = 1 αk yk = 0 ∑ n k = 1 αk = θ αk ≥ 0,k = 1,2,…,n 如此,可以通过二次规划的求解方法得到最优 解 α ∗ = [α ∗ 1 α ∗ 2 … α ∗ n ] T ,进而代入式(12)得 到 ωi 的最优解: ω ∗ i = 1 p - 1 p ∑ p i = 1 ∑ n k = 1 α ∗ k ykdi,k + ∑ n k = 1 α ∗ k ykdi,k 可以明显地观察到,即使成功的优化得到最优 解,也不能保证 ωi 完全满足式(2)中 ωi ≥ 0 的约束 条件,受 PFC 算法[11 ]的启发,在之前的基础上对 ωi 做如下修改: ωi = 0,i ∈ p - 1 p + - 1 p + ∑ j∈p +∑ n k = 1 α ∗ k ykdj,k + ∑ n k = 1 α ∗ k ykdi,k,i ∈ p + ì î í ï ï ïï (14) 式中: p - = {i:ωi = 0} p + = {i:ωi > 0} p + 表示所有使得 ωi 取正值的 i 的集合,相对应的 p - 表示无法使 ωi 取正值的 i 的集合,2 个集合 p + 和 p - 的大小分别使用 p + 和 p - 来表示。 至此完成求解距离分量权值 ωi 的目标,求解集 合 p + 和 p - 的算法描述将在下一小节给出。 最大几何间隔 ρ ‖ω‖ 中的 ρ 亦可在求解权值 ωi 的过程中求得。 与原始 SVM 类似,目标函数(3) 的分离超平面为 yk(∑ p i = 1 ωidi,k - β) = ρ ,即可得最大 函数间隔 ρ = yk(∑ p i = 1 ωidi,k - β) 。 在求得最优解后 由式(9)可得 β 的最优解 β ∗ = 1 2 ∑ n k = 1 α ∗ k yk 进而可得 最大函数间隔 ρ = yk(∑ p i = 1 ωi ∗ di,k - β ∗ ) 。 2.2 算法描述 本节将给出求解距离分量权值 ωi 的具体算法 步骤。 为了便于表示,将式(14)简化: ωi = 0,i ∈ p - 1 p + + CVi,i ∈ p + ì î í ï ï ïï (15) 式中: Vi = - 1 p + ∑ j∈p +∑ n k = 1 α ∗ k ykdj,k + ∑ n k = 1 α ∗ k ykdi,k (16) 由式(16)观察可得,若想满足 ωi 为正值,则 Vi 需要足够大,且当 Vi 越大, ωi 为正值的几率就越大。 因此,求解集合 p + 和 p - 的算法总结如下。 算法 1 求解集合 p + 和 p - 。 1)初始化: p + 0 = ∅,p - 0 = {1,2,…,p},h = 0; 2) h = h + 1,p + h = p + h-1 + {i},p - h = p - h-1 - {i}, 其 中, i = arg maxi∈p - h-1 {Vi} ; 3)通过式(14) 计算 ωg 并判断其是否大于 0。 其中, g = arg mini∈p + h {Vi} 。 如果 ωg > 0 则回到 2), 否则设置 p + = p + h-1 ,p - = p - h-1 并终止。 下面将介绍学习距离函数中权值 ωi 的算法,其 中 ωi 将采用如下方法初始化:在式(1)中 ωi 的约束 条件下,令 ω (0) 1 = ω (0) 2 = … = ω (0) p ,因此有 ω (0) i = 1 / p。 算法 2 学习距离函数。 输入: 1)数据矩阵: X ∈ R d×N ; 2)成对约束: x k a,x k a,yk ( ) 其中, yk = { + 1, - 1}; 3)参数: C、θ ; 输出:距离权值: ω ; ·846· 智 能 系 统 学 报 第 10 卷

第6期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 .847. 方法: 多类数据集。各个数据集的信息如表1所示。 1)初始化:w=w; 表1实验中使用的数据集信息 2)计算距离矩阵:D(i,k); Table 1 List of data sets 3)计算二次规划参数H和f: 数据集 样本数 特征数 类别数 H= breast 683 10 2 点(店三4dow小-日(含三4)+ sonar 208 60 2 wdbe 569 30 2 1A宫d heart 270 2 2 wine 178 13 3 4)利用二次规划优化算法求解得到最优解:α·= 1473 9 3 [aiag…ar]T; cme thyroid 215 3 5)计算集合p和p:算法1: 6)利用式(15)计算ω。 segment 2310 19 7 在数据集的选择上基于以下考虑:首先,这些数 3实验 据集的特征数和类别数都各不相同。另外,这些数 为了与传统CM算法之间有可比性,本文将简 据集是机器学习研究中被广泛使用的基准数据集, 单的以学习得到的距离函数替换传统FCM算法中 因而具有代表性。最后,由于数据集均为真实数据 的欧式距离。根据传统FCM算法的实现方法,本文 集,因此可以检验算法在真实应用中是否可行。 将通过以下步骤实现聚类: 文中所有实验均在MATLAB平台下进行,所有 训练数据集和测试数据集均先归一化至[0,1]内。 1)初始化隶属度矩阵U,使得 ∑4g=1,j= 带有边信息的训练集将通过如下方法产生:首先,随 1,2,…,n,u∈[0,1]。 机选取数据集的10%组成一个子集。然后,根据子 集中样本点带有的类标是否相同来生成约束对 2)计算聚类中心:c:= (x。,xy)集合。其中,类标相同的成对约束为正 约束对,反之为负约束对。将取个数相同的正负约 =1 束对组成训练集。 3)计算价值函数: 在组合距离分量的选择上,本文依据第2节的 94 J=) 理论,在实验中选取如下10个距离度量进行组合: d(x,y)=(x-y)1(x-y) 当其相对于上次价值函数值的改变量小于某个 阈值时,算法停止。 4)=(x-)rx-y) 4)更新隶属度矩阵: 1 d0x=21s- uj= =1 2/(m-1) d(x,y)=】 其中对于样本点x:,它与聚类中心c:之间的距 -31x 离使用如下公式计算: d6(x,y)=1-e2 d,=u,d(x,c) d(x,)=1-e 将上述聚类算法记为基于组合距离(hybrid dis- d(x,)=1-e tance)的FCM聚类算法(HDFCM)。 d,(x,)=1-eg 本节将上述HDCM算法与已有的经典距离学 dio(x,y)=1-e-lx12 习算法进行对比与分析。 在使用组合距离进行聚类的算法中,本文将依 3.1实验设置 据数据集的类别数给定聚类数目,初始隶属度矩阵 本文使用了8个来自UCI机器学习数据库的 随机生成。为了保证可比性,实验中所有的对比算 真实数据集。其中4个为二类数据集,其余4个为 法将使用相同的初始隶属度矩阵,训练集和其他参
方法: 1)初始化: ω = ω (0) ; 2)计算距离矩阵: D(i,k) ; 3)计算二次规划参数 H 和 f : H = ∑ p i = 1 ∑ n q = 1∑ n r = 1 di,qdi,r yq y ( r) - 1 d ∑ p i = 1 ∑ n k = 1 y ( kdi,k ) 2 + y 2 k f = 1 p ∑ p i = 1 ∑ n k = 1 ykdi,k 4)利用二次规划优化算法求解得到最优解: α ∗ = [α ∗ 1 α ∗ 2 … α ∗ n ] T ; 5)计算集合 p + 和 p - :算法 1; 6)利用式(15)计算 ω 。 3 实验 为了与传统 FCM 算法之间有可比性,本文将简 单的以学习得到的距离函数替换传统 FCM 算法中 的欧式距离。 根据传统 FCM 算法的实现方法,本文 将通过以下步骤实现聚类: 1)初始化隶属度矩阵 U ,使得 ∑ c i = 1 uij = 1,∀j = 1,2,…,n,uij ∈ [0,1] 。 2)计算聚类中心: ci = ∑ N j = 1 u m ij xj ∑ N j = 1 u m ij 。 3)计算价值函数: J = ∑ c i = 1 ∑ N j = 1 u m ij d 2 ij 当其相对于上次价值函数值的改变量小于某个 阈值时,算法停止。 4)更新隶属度矩阵: uij = 1 ∑ c k = 1 dij dkj æ è ç ö ø ÷ 2/ (m-1 ) 其中对于样本点 xj ,它与聚类中心 ci 之间的距 离使用如下公式计算: dij = ∑ p r = 1 ωrdr(xj,ci) 将上述聚类算法记为基于组合距离(hybrid dis⁃ tance)的 FCM 聚类算法(HDFCM)。 本节将上述 HDFCM 算法与已有的经典距离学 习算法进行对比与分析。 3.1 实验设置 本文使用了 8 个来自 UCI 机器学习数据库的 真实数据集。 其中 4 个为二类数据集,其余 4 个为 多类数据集。 各个数据集的信息如表 1 所示。 表 1 实验中使用的数据集信息 Table 1 List of data sets 数据集 样本数 特征数 类别数 breast 683 10 2 sonar 208 60 2 wdbc 569 30 2 heart 270 12 2 wine 178 13 3 cmc 1 473 9 3 thyroid 215 5 3 segment 2 310 19 7 在数据集的选择上基于以下考虑:首先,这些数 据集的特征数和类别数都各不相同。 另外,这些数 据集是机器学习研究中被广泛使用的基准数据集, 因而具有代表性。 最后,由于数据集均为真实数据 集,因此可以检验算法在真实应用中是否可行。 文中所有实验均在 MATLAB 平台下进行,所有 训练数据集和测试数据集均先归一化至 [0,1] 内。 带有边信息的训练集将通过如下方法产生:首先,随 机选取数据集的 10%组成一个子集。 然后,根据子 集中样本点带有的类标是否相同来生成约束对 x k a ,x k b,yk ( ) 集合。 其中,类标相同的成对约束为正 约束对,反之为负约束对。 将取个数相同的正负约 束对组成训练集。 在组合距离分量的选择上,本文依据第 2 节的 理论,在实验中选取如下 10 个距离度量进行组合: d1(x,y) = (x - y) T I(x - y) d3(x,y) = (x - y) T 3I σ 2 (x - y) d4(x,y) = ∑ d i = 1 xi - yi d5(x,y) = ∑ d i = 1 xi - yi σ 2 d6(x,y) = 1 - e -3‖x-y‖2 σ 2 d7(x,y) = 1 - e -‖x-y‖2 σ 2 d8(x,y) = 1 - e -‖x-y‖2 3σ 2 d9(x,y) = 1 - e -‖x-y‖2 5σ 2 d10(x,y) = 1 - e -‖x-y‖2 在使用组合距离进行聚类的算法中,本文将依 据数据集的类别数给定聚类数目,初始隶属度矩阵 随机生成。 为了保证可比性,实验中所有的对比算 法将使用相同的初始隶属度矩阵,训练集和其他参 第 6 期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 ·847·

·848. 智能系统学报 第10卷 数(m=2,e=10-5,T=100,C=10-5)。实验将重 算法一样应用于FCM聚类算法中以评价。 复每个聚类过程20次,实验结果取其均值。 3.3实验结果与分析 为了评估聚类效果,采用一种类似F,-measure 对于各个数据集,本文所提出算法与其他算法 的成对约束评价方法,评价参数包括:pairwise Preci- 在8个数据集上的实验结果对比如图1所示,其中 sion,pairwise Recall和pairwise F,定义为[ 每一个子图的纵坐标表示了各个算法在相同参数下 #TruePositive 在该数据集上的聚类效果的评价指标均值,横坐标 Precision #TruePositive +#FalsePositive 上的柱形分为3组,每一组分别表示F,、precsion和 #TruePositive Recall = recall。每个颜色代表一个算法,从左至右分别为 #TruePositive #FalseNegative FCM算法[a,C-Euc算法[),PGDM-Ad算法[), 2 X Precision×Recall F1= PGDM-Af算法[]和HDFCM算法,数据集名称标注 Precision Recall 在图标题上。表2展示了本文算法相对于传统 式中:#TruePositive为将正约束对预测为正约束对 FCM算法聚类效果的提升率,提升率使用如下公式 的个数,#FalsePositive为将负约束对预测为正约束 计算得到: 对的个数,#FalseNegative为将正约束对预测为负 HDFCM_F FCM_F 约束对的个数。由于该评价方法的对象为约束对, 提升率= -×100% FCM_F 因此不仅可以应用于二分类的评价,也可应用于多 从图1可以看出,本文提出的算法在大部分数 类分类的评价。 据集上获得了最好的表现。相对于其他距离学习算 3.2对比算法 法而言,本文算法在sonar数据集和cmc数据集中 本文使用了若干经典距离学习算法进行对比, 虽未获得最好的表现,但是结合表2可以发现本文 包括:使用欧式距离的传统FCM算法(FCM),使用 算法的聚类效果相对于传统CM算法仍有一定的 欧氏距离但含有约束条件的K-均值聚类算法(C- 提升。由于本文使用的距离分量有限,因此对于不 Ec)【2),基于凸优化的全局距离学习算法(PG 同的数据集不一定能拟合出最适合于该数据集的距 DM)[3] 离度量。此外,从表2可以观察到,本文算法在 与本文提出的算法类似,C-Euc算法也是一种利 breast数据集和wine数据集上有相当卓越的表现。 用边信息进行距离学习的半监督聚类算法,它在传统 结合图1和表1可以得出,本文算法不仅适用 K-均值算法的基础上加上成对约束,在这些约束的监 于2类数据集,对于多类数据集也有较好的聚类效 督下进行聚类。C-Euc算法在聚类的过程中要求每 果。比如,2类数据集breast,3类数据集wine,7类 一次划分都满足已知的约束条件,每个样本在没有违 数据集segment在聚类效果上均取得了30%以上的 反约束条件的情况下,被划分给最近的类,最终得到 提升。 的聚类结果将满足所有的约束对信息[]。 1.0 PGDM算法由Xing等提出,是一种基于凸优化 0.8 的全局距离度量学习算法。它将正约束对构成的集 合记为S,负约束对构成的集合记为D。通过以下 凸优化问题对距离矩阵A进行求解: FCM min∑Ix-x,I C-Euc (xi》eS 0.2 PGDM-Ad GDM-Af st.∑‖x-xI4≥1,A≥0 HDFCM ()eD F precision recall (a)breast 式中:Ⅱ:,‖A=√(x,)A(,x)表示2个 1.0 样本点x,和x之间的距离。根据预期得到的矩阵 0.8 A的不同将有不同的解法。如果期望得到对角形式 的距离矩阵,可以通过牛顿法进行求解,本文将此算 0.6 法记为PGDM-Ad。如果期待得到全矩阵形式的距 0.4 IFCM 离矩阵,则可以通过梯度下降和逐次映射的方法进 C-Euc 0.2 PGDM-Ad 行求解,本文将此算法记为PGDM-Af。为了保证对 PGDM-AF HDFCM 比性,在实验中本文将学习得到的距离矩阵和本文 precision recall (b)sonar
数( m = 2,ε = 10 -5 ,T = 100,C = 10 -5 )。 实验将重 复每个聚类过程 20 次,实验结果取其均值。 为了评估聚类效果,采用一种类似 F1 ⁃measure 的成对约束评价方法,评价参数包括:pairwise Preci⁃ sion,pairwise Recall 和 pairwise F1 , 定义为[2] Precision = #TruePositive #TruePositive + #FalsePositive Recall = #TruePositive #TruePositive + #FalseNegative F1 = 2 × Precision × Recall Precision + Recall 式中: #TruePositive 为将正约束对预测为正约束对 的个数, #FalsePositive 为将负约束对预测为正约束 对的个数, #FalseNegative 为将正约束对预测为负 约束对的个数。 由于该评价方法的对象为约束对, 因此不仅可以应用于二分类的评价,也可应用于多 类分类的评价。 3.2 对比算法 本文使用了若干经典距离学习算法进行对比, 包括:使用欧式距离的传统 FCM 算法(FCM),使用 欧氏距离但含有约束条件的 K⁃均值聚类算法(C⁃ Euc) [12 ] ,基于凸优化的全局距离学习算法 ( PG⁃ DM) [3] 。 与本文提出的算法类似,C⁃Euc 算法也是一种利 用边信息进行距离学习的半监督聚类算法,它在传统 K⁃均值算法的基础上加上成对约束,在这些约束的监 督下进行聚类。 C⁃Euc 算法在聚类的过程中要求每 一次划分都满足已知的约束条件,每个样本在没有违 反约束条件的情况下,被划分给最近的类,最终得到 的聚类结果将满足所有的约束对信息[13 ] 。 PGDM 算法由 Xing 等提出,是一种基于凸优化 的全局距离度量学习算法。 它将正约束对构成的集 合记为 S ,负约束对构成的集合记为 D 。 通过以下 凸优化问题对距离矩阵 A 进行求解: min A (x∑i ,xj )∈S ‖ xi - xj‖2 A s.t. (x∑i ,xj )∈D ‖ xi - xj‖A ≥ 1,A ≥ 0 式中: ‖ xi,xj‖A = (xi,xj) TA(xi,xj) 表示 2 个 样本点 xi 和 xj 之间的距离。 根据预期得到的矩阵 A 的不同将有不同的解法。 如果期望得到对角形式 的距离矩阵,可以通过牛顿法进行求解,本文将此算 法记为 PGDM⁃Ad。 如果期待得到全矩阵形式的距 离矩阵,则可以通过梯度下降和逐次映射的方法进 行求解,本文将此算法记为 PGDM⁃Af。 为了保证对 比性,在实验中本文将学习得到的距离矩阵和本文 算法一样应用于 FCM 聚类算法中以评价。 3.3 实验结果与分析 对于各个数据集,本文所提出算法与其他算法 在 8 个数据集上的实验结果对比如图 1 所示,其中 每一个子图的纵坐标表示了各个算法在相同参数下 在该数据集上的聚类效果的评价指标均值,横坐标 上的柱形分为 3 组,每一组分别表示 F1 、precsion 和 recall。 每个颜色代表一个算法,从左至右分别为 FCM 算法[ 14 ] , C⁃Euc 算法[12] , PGDM⁃Ad 算法[3] , PGDM⁃Af 算法[3]和 HDFCM 算法,数据集名称标注 在图标题上。 表 2 展示了本文算法相对于传统 FCM 算法聚类效果的提升率,提升率使用如下公式 计算得到: 提升率 = HDFCM_F1 - FCM_F1 FCM_F1 × 100% 从图 1 可以看出,本文提出的算法在大部分数 据集上获得了最好的表现。 相对于其他距离学习算 法而言,本文算法在 sonar 数据集和 cmc 数据集中 虽未获得最好的表现,但是结合表 2 可以发现本文 算法的聚类效果相对于传统 FCM 算法仍有一定的 提升。 由于本文使用的距离分量有限,因此对于不 同的数据集不一定能拟合出最适合于该数据集的距 离度量。 此外,从表 2 可以观察到, 本文算法在 breast 数据集和 wine 数据集上有相当卓越的表现。 结合图 1 和表 1 可以得出,本文算法不仅适用 于 2 类数据集,对于多类数据集也有较好的聚类效 果。 比如,2 类数据集 breast,3 类数据集 wine,7 类 数据集 segment 在聚类效果上均取得了 30%以上的 提升。 ·848· 智 能 系 统 学 报 第 10 卷
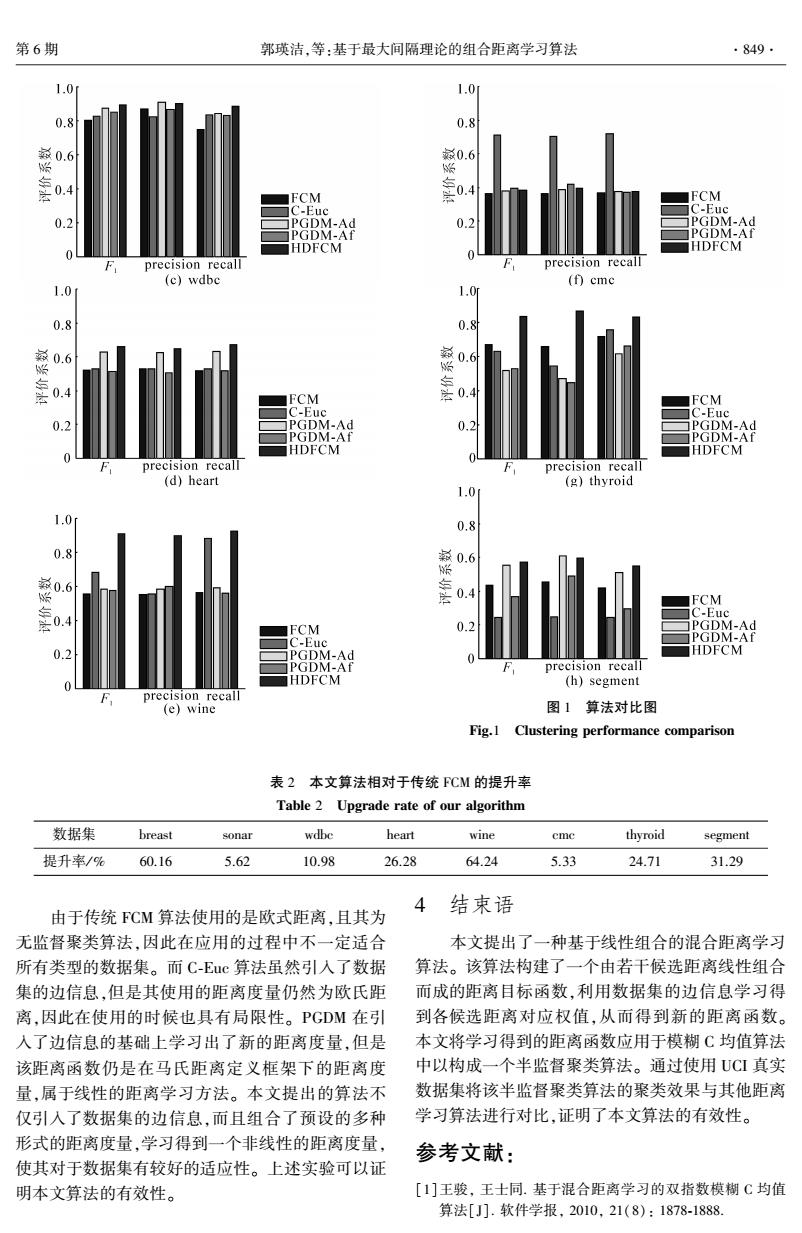
第6期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 ·849. 1.0 1.01 0.8 0.8 0.6 敏0.6 0.4 FCM IFCM C-Euc C-Euc 0.2 PGDM-Ad 0.2 PGDM-Ad PGDM-Af PGDM-Af HDFCM HDFCM precision recal precision recall (c)wdbe (f)cme 1.0 1.0 0.8 0.8 0.6 FCM FCM C-Euc C-Euc 02 PGDM-Ad 0 PGDM-Ad PGDM-Af PGDM-Af HDFCM HDFCM precision recal precision recall (d)heart (g)thyroid 1.0 .0 0.8 0.8 0.6 0.6 0. FCM C-Euc .4 FCM PGDM-Ad C-Euc PGDM-Af 0.2 PGDM-Ad HDECM PGDM-Af precision recall HDFCM (h)segment precision recall (e)wine 图1算法对比图 Fig.1 Clustering performance comparison 表2本文算法相对于传统FCM的提升率 Table 2 Upgrade rate of our algorithm 数据集 breast sonar wdbe heart wine cmc thyroid segment 提升率/% 60.16 5.62 10.98 26.28 64.24 5.33 24.71 31.29 4 由于传统FCM算法使用的是欧式距离,且其为 结束语 无监督聚类算法,因此在应用的过程中不一定适合 本文提出了一种基于线性组合的混合距离学习 所有类型的数据集。而C-Euc算法虽然引入了数据 算法。该算法构建了一个由若干候选距离线性组合 集的边信息,但是其使用的距离度量仍然为欧氏距 而成的距离目标函数,利用数据集的边信息学习得 离,因此在使用的时候也具有局限性。PGDM在引 到各候选距离对应权值,从而得到新的距离函数。 入了边信息的基础上学习出了新的距离度量,但是 本文将学习得到的距离函数应用于模糊C均值算法 该距离函数仍是在马氏距离定义框架下的距离度 中以构成一个半监督聚类算法。通过使用UCI真实 量,属于线性的距离学习方法。本文提出的算法不 数据集将该半监督聚类算法的聚类效果与其他距离 仅引入了数据集的边信息,而且组合了预设的多种 学习算法进行对比,证明了本文算法的有效性。 形式的距离度量,学习得到一个非线性的距离度量, 参考文献: 使其对于数据集有较好的适应性。上述实验可以证 明本文算法的有效性。 [1]王骏,王士同.基于混合距离学习的双指数模糊C均值 算法[J].软件学报,2010,21(8):1878-1888
图 1 算法对比图 Fig.1 Clustering performance comparison 表 2 本文算法相对于传统 FCM 的提升率 Table 2 Upgrade rate of our algorithm 数据集 breast sonar wdbc heart wine cmc thyroid segment 提升率/ % 60.16 5.62 10.98 26.28 64.24 5.33 24.71 31.29 由于传统 FCM 算法使用的是欧式距离,且其为 无监督聚类算法,因此在应用的过程中不一定适合 所有类型的数据集。 而 C⁃Euc 算法虽然引入了数据 集的边信息,但是其使用的距离度量仍然为欧氏距 离,因此在使用的时候也具有局限性。 PGDM 在引 入了边信息的基础上学习出了新的距离度量,但是 该距离函数仍是在马氏距离定义框架下的距离度 量,属于线性的距离学习方法。 本文提出的算法不 仅引入了数据集的边信息,而且组合了预设的多种 形式的距离度量,学习得到一个非线性的距离度量, 使其对于数据集有较好的适应性。 上述实验可以证 明本文算法的有效性。 4 结束语 本文提出了一种基于线性组合的混合距离学习 算法。 该算法构建了一个由若干候选距离线性组合 而成的距离目标函数,利用数据集的边信息学习得 到各候选距离对应权值,从而得到新的距离函数。 本文将学习得到的距离函数应用于模糊 C 均值算法 中以构成一个半监督聚类算法。 通过使用 UCI 真实 数据集将该半监督聚类算法的聚类效果与其他距离 学习算法进行对比,证明了本文算法的有效性。 参考文献: [1]王骏, 王士同. 基于混合距离学习的双指数模糊 C 均值 算法[J]. 软件学报, 2010, 21(8): 1878⁃1888. 第 6 期 郭瑛洁,等:基于最大间隔理论的组合距离学习算法 ·849·

.850. 智能系统学报 第10卷 WANG Jun,WANG Shitong.Double indices FCM algorithm [10]TSANG I W H,KWOK J T Y,ZURADA J A.Generalized based on hybrid distance metric learning[J].Journal of Soft- Core Vector Machines [J].IEEE Transaction on Neural ware,2010,21(8):1878-1888. Networks,2006,17(5):1126-1140. [2]WU Lei,HOI S C H,JIN Rong,et al.Learning Bregman [11]MEI Jianping,CHEN Lihui.Fuzzy clustering with weighted distance functions for semi-supervised clustering[J].IEEE medoids for relational data[J].Pattern Recognition,2010, Transactions on Knowledge and Data Engineering,2012,24 43(5):1964-1974. (3):478-491. [12]WAGSTAFF K,CARDIE C,ROGERS S,et al.Constrain- [3]XING E P,NG A Y,JORDAN M I,et al.Distance metric ed k-means clustering with background knowledge C]// learning with application to clustering with side information BAR-HILLEL A,HERTZ T,SHENTAL N,et al.Proceed- [C]//Advances in Neural Information Processing Systems. ings of the Eighteenth International Conference on Machine Vancouver,Canada,2002:521-528. Learning.Williamstown,Australia,2001:577-584. [4]HOI S C H,LIU Wei,LYU M R,et al.Learning distance [13]COVOES T F,HRUSCHKA E R,GHOSH J.A study of k- metrics with contextual constraints for image retrieval[C]// means-based algorithms for constrained clustering[J].In- Proceedings of 2006 IEEE Computer Society Conference on telligent Data Analysis,2013,17(3):485-505. Computer Vision and Pattern Recognition.New York,Amer- [14]BEZDEK J C.Pattern recognition with fuzzy objective func- ica,2006,2:2072-2078. tion algorithms[M.New York:Plenum Press,1981:56- [5]GOLDBERGER J,HINTON G,ROWEIS S,et al.Neigh- 57. borhood component analysis[C]//Advances in Neural Infor- 作者简介: mation Processing Systems.Cambridge,United Kingdom, 郭瑛洁,女,1991生,硕士研究生, 2005:451-458. 主要研究方向为人工智能,模式识别。 [6]WEINBERGER K Q,BLITZER J C,SAUL L K.Distance metric learning for large margin nearest neighbor classifica- tion[C]//Advances in Neural Information Processing Sys- tems.Cambridge,United Kingdom,2006:1473-1480. [7]王骏,王土同,邓赵红.特征加权距离与软子空间学习 相结合的文本聚类新方法[J].计算机学报,2012,35 王士同,男,1964生,教授,博士生 (8):1655-1665. 导师,主要研究方向为人工智能、模式 WANG Jun,WANG Shitong,DENG Zhaohong.A novel text 识别和生物信息。 clustering algorithm based on feature weighting distance and soft subspace learning[J].Chinese Journal of Computers, 2012,35(8):1655-1665. [8]WU K L,YANG M S.Alternative c-means clustering algo- 许小龙,男,1989生,硕士研究生, rithms J].Pattern Recognition,2002,35 (10):2267- 主要研究方向为人工智能,模式识别。 2278. [9]CORTES C.VAPNIK V.Support-vector networks[J].Ma- chine Learning,1995,20(3):273-297
WANG Jun, WANG Shitong. Double indices FCM algorithm based on hybrid distance metric learning[J]. Journal of Soft⁃ ware, 2010, 21(8): 1878⁃1888. [2]WU Lei, HOI S C H, JIN Rong, et al. Learning Bregman distance functions for semi⁃supervised clustering[ J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24 (3): 478⁃491. [3]XING E P, NG A Y, JORDAN M I, et al. Distance metric learning with application to clustering with side information [C] / / Advances in Neural Information Processing Systems. Vancouver, Canada, 2002: 521⁃528. [4]HOI S C H, LIU Wei, LYU M R, et al. Learning distance metrics with contextual constraints for image retrieval[C] / / Proceedings of 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York, Amer⁃ ica, 2006, 2: 2072⁃2078. [5]GOLDBERGER J, HINTON G, ROWEIS S, et al. Neigh⁃ borhood component analysis[C] / / Advances in Neural Infor⁃ mation Processing Systems. Cambridge, United Kingdom, 2005: 451⁃458. [6]WEINBERGER K Q, BLITZER J C, SAUL L K. Distance metric learning for large margin nearest neighbor classifica⁃ tion[ C] / / Advances in Neural Information Processing Sys⁃ tems. Cambridge, United Kingdom, 2006: 1473⁃1480. [7]王骏, 王士同, 邓赵红. 特征加权距离与软子空间学习 相结合的文本聚类新方法[ J]. 计算机学报, 2012, 35 (8): 1655⁃1665. WANG Jun, WANG Shitong, DENG Zhaohong. A novel text clustering algorithm based on feature weighting distance and soft subspace learning [ J]. Chinese Journal of Computers, 2012, 35(8): 1655⁃1665. [8]WU K L, YANG M S. Alternative c⁃means clustering algo⁃ rithms[ J]. Pattern Recognition, 2002, 35 ( 10 ): 2267⁃ 2278. [9]CORTES C, VAPNIK V. Support⁃vector networks[ J]. Ma⁃ chine Learning, 1995, 20(3): 273⁃297. [10]TSANG I W H, KWOK J T Y, ZURADA J A. Generalized Core Vector Machines [ J]. IEEE Transaction on Neural Networks, 2006, 17(5): 1126⁃1140. [11]MEI Jianping, CHEN Lihui. Fuzzy clustering with weighted medoids for relational data[J]. Pattern Recognition, 2010, 43(5): 1964⁃1974. [12]WAGSTAFF K, CARDIE C, ROGERS S, et al. Constrain⁃ ed k⁃means clustering with background knowledge [ C] / / BAR⁃HILLEL A, HERTZ T, SHENTAL N, et al. Proceed⁃ ings of the Eighteenth International Conference on Machine Learning. Williamstown, Australia,2001: 577⁃584. [13]COVÕES T F, HRUSCHKA E R, GHOSH J. A study of k⁃ means⁃based algorithms for constrained clustering[ J]. In⁃ telligent Data Analysis, 2013, 17(3): 485⁃505. [14]BEZDEK J C. Pattern recognition with fuzzy objective func⁃ tion algorithms[M]. New York: Plenum Press, 1981: 56⁃ 57. 作者简介: 郭瑛洁,女,1991 生,硕士研究生, 主要研究方向为人工智能、模式识别。 王士同,男,1964 生,教授,博士生 导师,主要研究方向为人工智能、模式 识别和生物信息。 许小龙,男,1989 生,硕士研究生, 主要研究方向为人工智能、模式识别。 ·850· 智 能 系 统 学 报 第 10 卷