
第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Aug.2015 D0:10.3969/j.issn.1673-4785.201411025 网络出版地址:htp:/www.cnki.net/kcms/detail/23.1538.tp.20150716.0934.002.html 基于近似消息传递算法的压缩感知雷达成像方法 唐琳,焦淑红 (哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001) 摘要:针对大观测矩阵引起的压缩感知面达成像高计算量的问题,提出了一种基于近似观测模型的近似消息传递 算法,通过引入逆线调频变标算子,压缩感知雷达成像中的大观测矩阵能够得到很好的近似,从而能够有效地运用 现有的成熟的去耦合措施来降低压缩感知雷达成像的计算量:同时,通过引入近似的消息传递,新算法获得了不错 的收敛速度。理论分析和仿真实验表明,新算法能够实现非完全观测数据的压缩感知面达成像,与现有的同类压缩 感知雷达成像方法相比,其在保证不增加单步迭代计算量的同时,具有更高的收敛速度。 关键词:面达成像:压缩感知:近似观测模型:消息传递:置信传播 中图分类号:TN951文献标志码:A文章编号:1673-4785(2015)04-0592-07 中文引用格式:唐琳,焦淑红.基于近似消息传递算法的压缩感知雷达成像方法[J].智能系统学报,2015,10(4):592-598. 英文引用格式:TANG Lin,JIAO Shuhong.Compressed sensing radar imaging using approximate message passing[J].CAAl Transactions on Intelligent Systems,2015,10(4):592-598. Compressed sensing radar imaging using approximate message passing TANG Lin,JIAO Shuhong (College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China) Abstract:In order to solve the great computational complexity in compressed sensing radar imaging due to a large observation matrix,an approximate observation model based approximate message passing algorithm is proposed in this paper.It uses inverse chirp scaling operator to approximate the large observation matrix in compressed sensing radar imaging,thereby effectively reducing the computational complexity by the current mature decoupling technolo- gy,and in the meantime,the approximate message passing is used to improve convergence rate.The theoretical a- nalysis and simulation show that compared to the currently used compressed sensing radar imaging methods,the proposed method exhibits higher convergence rate while suffers same computational complexity in each iteration.It realizes compressed sensing radar imaging of non-complete observation data. Keywords:radar imaging;compressed sensing;approximate observation model;approximate message pass- ing:belief propagation 雷达成像是一种全天时、全天候的主动信息获 功能、多任务以及抗干扰特点,都会不可避免地产生 取手段,然而受奈奎斯特采样准则的限制,传统基于 非完全观测数据,这也进一步要求雷达成像方法具 匹配滤波的高分辨雷达成像面临高数据率的问题, 有非完全数据的的处理能力[2。目前,压缩感知 这就需要研究出低奈奎斯特采样下的非完全观测数 技术使得非完全观测数据下的稀疏信息恢复成为可 据处理方法],除此之外,复杂电磁环境下雷达多 能1。由于它能够满足雷达成像中处理非完全数 据的需求,因此结合了压缩感知技术和雷达成像技 收稿日期:2014-11-22.网络出版日期:2015-07-16. 基金项目:国家自然科学基金资助项目(61201410). 术的压缩感知雷达成像方法成为近年来人们研究的 通信作者:唐琳.E-mail:tanglinheu(@163.com. 热点s刀。通常情况下,压缩感知雷达成像方法不
第 10 卷第 4 期 智 能 系 统 学 报 Vol.10 №.4 2015 年 8 月 CAAI Transactions on Intelligent Systems Aug. 2015 DOI:10.3969 / j.issn.1673⁃4785.201411025 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150716.0934.002.html 基于近似消息传递算法的压缩感知雷达成像方法 唐琳,焦淑红 (哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001) 摘 要:针对大观测矩阵引起的压缩感知雷达成像高计算量的问题,提出了一种基于近似观测模型的近似消息传递 算法,通过引入逆线调频变标算子,压缩感知雷达成像中的大观测矩阵能够得到很好的近似,从而能够有效地运用 现有的成熟的去耦合措施来降低压缩感知雷达成像的计算量;同时,通过引入近似的消息传递,新算法获得了不错 的收敛速度。 理论分析和仿真实验表明,新算法能够实现非完全观测数据的压缩感知雷达成像,与现有的同类压缩 感知雷达成像方法相比,其在保证不增加单步迭代计算量的同时,具有更高的收敛速度。 关键词:雷达成像;压缩感知;近似观测模型:消息传递;置信传播 中图分类号: TN951 文献标志码:A 文章编号:1673⁃4785(2015)04⁃0592⁃07 中文引用格式:唐琳,焦淑红. 基于近似消息传递算法的压缩感知雷达成像方法[J]. 智能系统学报, 2015, 10(4): 592⁃598. 英文引用格式:TANG Lin, JIAO Shuhong. Compressed sensing radar imaging using approximate message passing [ J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 592⁃598. Compressed sensing radar imaging using approximate message passing TANG Lin, JIAO Shuhong (College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China) Abstract:In order to solve the great computational complexity in compressed sensing radar imaging due to a large observation matrix, an approximate observation model based approximate message passing algorithm is proposed in this paper. It uses inverse chirp scaling operator to approximate the large observation matrix in compressed sensing radar imaging, thereby effectively reducing the computational complexity by the current mature decoupling technolo⁃ gy, and in the meantime, the approximate message passing is used to improve convergence rate. The theoretical a⁃ nalysis and simulation show that compared to the currently used compressed sensing radar imaging methods, the proposed method exhibits higher convergence rate while suffers same computational complexity in each iteration. It realizes compressed sensing radar imaging of non⁃complete observation data. Keywords:radar imaging; compressed sensing; approximate observation model; approximate message pass⁃ ing; belief propagation 收稿日期:2014⁃11⁃22. 网络出版日期:2015⁃07⁃16. 基金项目:国家自然科学基金资助项目(61201410). 通信作者:唐琳. E⁃mail:tanglinheu@ 163.com. 雷达成像是一种全天时、全天候的主动信息获 取手段,然而受奈奎斯特采样准则的限制,传统基于 匹配滤波的高分辨雷达成像面临高数据率的问题, 这就需要研究出低奈奎斯特采样下的非完全观测数 据处理方法[1] ,除此之外,复杂电磁环境下雷达多 功能、多任务以及抗干扰特点,都会不可避免地产生 非完全观测数据,这也进一步要求雷达成像方法具 有非完全数据的的处理能力[2⁃3] 。 目前,压缩感知 技术使得非完全观测数据下的稀疏信息恢复成为可 能[4] 。 由于它能够满足雷达成像中处理非完全数 据的需求,因此结合了压缩感知技术和雷达成像技 术的压缩感知雷达成像方法成为近年来人们研究的 热点[5⁃7] 。 通常情况下,压缩感知雷达成像方法不

第4期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 ·593· 仅能够降低雷达成像的数据率,同时还能够提高雷 天线位置决定的回波时延;p(·)为雷达波形中的 达成像的质量,这使它得到迅猛的发展。不过,压缩 基带信号;f为雷达载频:n(·)为观测噪声,一般情 感知雷达成像的实现是以目标具有稀疏性作为前提 况下可以认为是高斯白噪声。离散化观测场景,同 的,实际上,在雷达成像中对于某些特殊场景如海面 时对回波进行离散采样,可以获得雷达回波精确的 舰船目标等来说,该前提是自然成立的,到目前为 离散观测模型如下: 止,针对压缩感知雷达成像问题,研究者们进行了大 y=O+n=⊙Hx+n=Φx+n(2) 量卓有成效的研究,其中,文献[7-10]给出了基于精 式中:s∈C、n∈C分别表示离散回波和噪声:当 确观测模型的压缩感知雷达成像方法,虽然这些方 X∈Cx,Y∈Cmm分别表示二维离散的观测场景 法能够大幅提高雷达成像的质量,但是由于雷达成 和二维离散回波矩阵时,y=vec(Y)∈Cm表示经采 像中距离向与方位向的耦合,使得观测矩阵过于庞 样后的回波向量,x=vec(X)∈C表示场景中各离 大,成像过程将面临大存储量和高计算量,这使得这 散散射点组成的散射系数向量,vec(·)为向量化算 些压缩感知雷达成像方法难于实现,在此基础上,文 子:O=⊙⑧O,eCmx表示下采样矩阵,⑧表示Ko 献[11-12]给出了基于近似观测模型的压缩感知雷 necker积,⊙,和⊙。分别表示距离向和方位向的下 达成像方法,这类方法使用距离多普勒算子或是线 采样矩阵:重∈CmxN为感知矩阵;H∈CxN为观测矩 调频变标算子来获得近似的观测矩阵,利用迭代收 阵,它与式(1)中发射信号的波形有关。 缩阈值(iterative shrinkage thresholding,IST)算法实 实际上,雷达成像问题就是利用式(2)所示的 现雷达成像,得益于传统成像算法的解耦合操作,距 精确观测模型,从离散回波中恢复观测场景的问题, 离向和方位向操作可以分开处理,从而有效地降低 当雷达场景为空域稀疏的场景时,雷达成像问题可 压缩感知雷达成像单步迭代的计算量。这使得压缩 以转化为式(4)所示的优化问题: 感知雷达成像的效率明显提高,然而值得注意的是: arg minyp (3) 压缩感知雷达成像的运算量不仅与单步迭代的计算 量有关,而且与具体的算法选择也存在一定的关系, 式中入为正则化参数,它和目标稀疏性有关。上述 受ST算法收敛慢的影响,这类方法的总体计算量 问题被称作最小绝对收缩和变量选择(the least ab 依然十分可观。实际上,为了解决ST算法收敛慢 solute shrinkage and selectionator operator,LASSO) 的问题,文献[13-15]给出了基于置信传播理论的近 题,实现空域稀疏场景雷达成像的过程就是求解上 似消息传递(approximate message passing,AMP)算 述LASS0问题的过程。 法,它无论在收敛速度和恢复质量以及算法评估方 2成像算法 面都表现出比较独特的优势,非常适合大观测矩阵 的压缩感知问题,然而如果将其应用到压缩感知雷 2.1近似消息传递算法 达成像中,势必和其他迭代收缩类算法一样面临大 如式(3)所示的LASS0问题实际上可以通过 观测矩阵带来的大存储量和大计算量问题。有鉴于 AMP算法来求解],AMP算法是一种通过置信传 此,本文给出一种结合近似观测模型和近似消息传 播理论来求取变量空间边缘概率密度分布的迭代算 递算法的新方法来实现压缩感知雷达成像,利用近 法,与一般的置信传播算法不同,AMP算法通过利 似观测模型来降低单步迭代产生的计算量和存储 用中心极限定理以及泰勒展开来进行近似,能够极 量,利用近似消息传递算法来提高算法的收敛速度。 大地降低消息传递所带来的计算量。通常情况下, 一阶的近似消息传递算法可以使用式(4)所示的迭 1信号模型 代过程来表示。 雷达成像中,雷达接收到的回波可以建模成发 x+1=μ(Φz+x,y) 射的雷达波形与反射区域目标分布的二维卷积,对 k=y-r1+后(w+,y)》4 于某一观测场景A,雷达经去载频后的回波为 式中:x为目标场景的当前估计;z为当前的残差, s(v)=x(u)exp(-j2mfi(v-u))p(v- Y为当前选取的软阈值;μ(x,Y)为软阈值算子; u)o(p-u)du+n(v) (1) (x,Y)为u(x,y)的一阶导数;δ是由观测模型决定 式中:s(·)为去载频后的回波;x(u)表示场景中 的数据采样率。 位于处的散射点的散射系数;y表示天线的时间- 近似消息传递算法的迭代过程与迭代收缩阈值 空间位置;(·)表示天线的加权;(·)为目标和 算法大体相同,因此其单步迭代产生的计算量与
仅能够降低雷达成像的数据率,同时还能够提高雷 达成像的质量,这使它得到迅猛的发展。 不过,压缩 感知雷达成像的实现是以目标具有稀疏性作为前提 的,实际上,在雷达成像中对于某些特殊场景如海面 舰船目标等来说,该前提是自然成立的,到目前为 止,针对压缩感知雷达成像问题,研究者们进行了大 量卓有成效的研究,其中,文献[7⁃10]给出了基于精 确观测模型的压缩感知雷达成像方法,虽然这些方 法能够大幅提高雷达成像的质量,但是由于雷达成 像中距离向与方位向的耦合,使得观测矩阵过于庞 大,成像过程将面临大存储量和高计算量,这使得这 些压缩感知雷达成像方法难于实现,在此基础上,文 献[11⁃12]给出了基于近似观测模型的压缩感知雷 达成像方法,这类方法使用距离多普勒算子或是线 调频变标算子来获得近似的观测矩阵,利用迭代收 缩阈值(iterative shrinkage thresholding, IST)算法实 现雷达成像,得益于传统成像算法的解耦合操作,距 离向和方位向操作可以分开处理,从而有效地降低 压缩感知雷达成像单步迭代的计算量。 这使得压缩 感知雷达成像的效率明显提高,然而值得注意的是: 压缩感知雷达成像的运算量不仅与单步迭代的计算 量有关,而且与具体的算法选择也存在一定的关系, 受 IST 算法收敛慢的影响,这类方法的总体计算量 依然十分可观。 实际上,为了解决 IST 算法收敛慢 的问题,文献[13⁃15]给出了基于置信传播理论的近 似消息传递( approximate message passing, AMP) 算 法,它无论在收敛速度和恢复质量以及算法评估方 面都表现出比较独特的优势,非常适合大观测矩阵 的压缩感知问题,然而如果将其应用到压缩感知雷 达成像中,势必和其他迭代收缩类算法一样面临大 观测矩阵带来的大存储量和大计算量问题。 有鉴于 此,本文给出一种结合近似观测模型和近似消息传 递算法的新方法来实现压缩感知雷达成像,利用近 似观测模型来降低单步迭代产生的计算量和存储 量,利用近似消息传递算法来提高算法的收敛速度。 1 信号模型 雷达成像中,雷达接收到的回波可以建模成发 射的雷达波形与反射区域目标分布的二维卷积,对 于某一观测场景 A ,雷达经去载频后的回波为 s(v) = ∫ A x(u)exp( - j2πfι(v - u))p(v - u)w(v - u)du + n(v) (1) 式中: s(·) 为去载频后的回波; x ( u)表示场景中 位于 u 处的散射点的散射系数;v 表示天线的时间- 空间位置; w(·) 表示天线的加权; ι(·) 为目标和 天线位置决定的回波时延; p(·) 为雷达波形中的 基带信号; f 为雷达载频; n(·) 为观测噪声,一般情 况下可以认为是高斯白噪声。 离散化观测场景,同 时对回波进行离散采样,可以获得雷达回波精确的 离散观测模型如下: y = Θs + n = ΘHx + n = Φx + n (2) 式中:s∈C N 、n∈C m 分别表示离散回波和噪声;当 X∈C Nr ×Na ,Y∈C mr ×ma分别表示二维离散的观测场景 和二维离散回波矩阵时,y = vec(Y)∈C m 表示经采 样后的回波向量,x = vec(X)∈C N 表示场景中各离 散散射点组成的散射系数向量,vec(·)为向量化算 子;Θ= Θ T aΘr∈C m×N表示下采样矩阵,表示 Kro⁃ necker 积,Θr 和 Θa 分别表示距离向和方位向的下 采样矩阵;Φ∈C m×N为感知矩阵;H∈C N×N为观测矩 阵,它与式(1)中发射信号的波形有关。 实际上,雷达成像问题就是利用式(2) 所示的 精确观测模型,从离散回波中恢复观测场景的问题, 当雷达场景为空域稀疏的场景时,雷达成像问题可 以转化为式(4)所示的优化问题: arg min x λ‖x‖1 + 1 2 ‖y - Φx‖2 { 2} (3) 式中 λ 为正则化参数,它和目标稀疏性有关。 上述 问题被称作最小绝对收缩和变量选择( the least ab⁃ solute shrinkage and selectionator operator, LASSO)问 题,实现空域稀疏场景雷达成像的过程就是求解上 述 LASSO 问题的过程。 2 成像算法 2.1 近似消息传递算法 如式(3) 所示的 LASSO 问题实际上可以通过 AMP 算法来求解[13] ,AMP 算法是一种通过置信传 播理论来求取变量空间边缘概率密度分布的迭代算 法,与一般的置信传播算法不同,AMP 算法通过利 用中心极限定理以及泰勒展开来进行近似,能够极 大地降低消息传递所带来的计算量。 通常情况下, 一阶的近似消息传递算法可以使用式(4)所示的迭 代过程来表示。 x t+1 = μ(Φ H z t + x t ,γ t ) z t+1 = y - Φx t+1 + 1 δ z t 〈μ′(Φ H z t + x t ,γ t )〉 ì î í ïï ï (4) 式中:x t 为目标场景的当前估计;z t 为当前的残差, γ t 为当前选取的软阈值;μ( x,γ)为软阈值算子;μ′ (x,γ)为 μ(x,γ)的一阶导数;δ 是由观测模型决定 的数据采样率。 近似消息传递算法的迭代过程与迭代收缩阈值 算法大体相同,因此其单步迭代产生的计算量与 第 4 期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 ·593·

·594. 智能系统学报 第10卷 IST算法相当。唯一不同在于AMP算法比IST 的优化问题。 算法多了一个软阈值算子的导数项(通常被称为 (x1n=()1 (9 Onsager项),得益于Onsager项,AMP算法能够获得 i1 更高的收敛速度,同时其重建效果也要明显优于 式中Z为该分布的归一化常数。当B→∞时,上述 IST算法[s),因此它将更适合于实际中的雷达成像。 分布将在式(7)所示的稀疏解处聚集。这就意味着 然而,值得注意的是,式(4)中的感知矩阵Φ依 只要能够求取上述分布的边缘概率密度分布,即可 赖于如式(2)所示的精确观测模型,距离向和方位 获得式(7)所示优化问题的稀疏解,因此该雷达成 向的耦合使得它的规模极其庞大,这使得如式(4) 像问题的求解过程实际上就是B→o时式(10)所示 所示AMP算法雷达成像面临高存储量大计算量的 分布边缘概率密度分布的求解过程。虽然精确的求 问题,物理实现将非常困难。 取上述分布的边缘概率密度分布非常困难,但是通 2.2基于近似观测模型的近似消息传递算法 过置信传播理论可以获得该边缘概率密度分布的近 通常情况下,典型的雷达成像算法如距离多普 似结果。 勒算法、线调频变标算法等利用去耦合措施,能够有 为了利用置信传播理论来求解边缘概率密度分 效地解决高存储量和大计算量问题:同时,在复杂场 布,首先需要以X,X2,…,Xx作为变量节点,以Y, 景的雷达回波的仿真中,利用逆线调频变标算子来 Y,…,Ym作为因子节点,以任意变量节点和因子节 构造回波能够有效降低计算量。鉴于此,本文试图 点之间的关系作为边构造双向因子图,然后可以通 通过逆线调频变标算子来近似回波,同时结合采样 过下述的和-积形式的置信传播理论来求取相应的 矩阵的Kronecker积形式,以期解决AMP算法在压 边缘概率密度分布: 缩感知成像中遇到的高存储量大计算量问题。由逆 m,(X)=p(X)Πm(X) 线调频变标算法可知,式(2)所示观测矩阵H可以 keMi)y (10) 使用式(5)所示逆线调频变标算子来近似表示【6。 m(X.)=p(Y,I x)II m(x)dx-i H≈FHP3FP2FPF。 (5) 式中:F。,F,∈C分别为方位向和距离向傅里叶变 式中:N(i)表示与节点i相邻的节点的集合, 换矩阵,它们都可以表示为DT矩阵与单位矩阵的 N(i)y表示除节点j以外与节点i相邻的节点的集 Kronecker积;对角矩阵P1、P,、P,∈Cxw为逆线调频 合,X表示除了X,以外的所有变量节点,m:,(X) 变标过程中各步骤进行相位补偿的相位矩阵。因 和m(X)为节点之间传递的消息。则如式(9)所 此,与观测矩阵有关的矩阵向量乘积可以表示为如 示分布的边缘概率密度分布可以表示为 下的形式: p(XIY)=p(X)Πm-(X) (11)》 keN(i) Hx vec(Tics(X));H"y vec(Tcs(Y))(6) 通过假设m,,(X:)表征变量的三阶矩有界,可 式中:Ts(·)和Tc(·)分别表示线调频变标算子 知m,(X)可以使用高斯分布进行近似,而m:y 和逆线调频变标算子:X、Y分别表示二维离散的观测 (X)可以近似认为具有高斯分布与拉普拉斯分布 场景和二维离散回波矩阵。因此,使用近似观测模型 的乘积形式,当B→∞时,通过一阶近似,基于近似 的雷达成像可以转化为如式(7)所示的优化问题: 观测模型的置信传播算法可以通过下面的迭代过程 arg minY( 来实现,本文将该新算法称作基于近似观测模型的 AMP算法。 (7) 当雷达场景由少数强散射点构成时,X可以认 [X=Tcs(⊙Z-⊙)+X- 为是一个具有空域稀疏性的稀疏信号,因此可以认 X=u(x,A +y') 为目标服从拉普拉斯分布,同时,不失一般性,观 测噪声可以认为服从高斯分布,即 Z=y-8,T(X)0.+Z'(x+y)》 (p(X;)=exp(-BAX) p(g10=em2g-(or黑a,月 =A有(A+y) (12) (8) 式中:u(a,b)表示软阈值算子,u'(a,b)为其一阶 式中:(·):表示矩阵的第i个元素;B为常数。此时 导数:8=m/N表示数据采样率;〈·〉为求取均值。 可以构造如式(9)所示后验分布来解决式(7)所示 上述算法流程可以正式描述如下:
IST 算法相当[12] 。 唯一不同在于 AMP 算法比 IST 算法多了一个软阈值算子的导数项(通常被称为 Onsager 项),得益于 Onsager 项,AMP 算法能够获得 更高的收敛速度,同时其重建效果也要明显优于 IST 算法[15] ,因此它将更适合于实际中的雷达成像。 然而,值得注意的是,式(4)中的感知矩阵 Φ 依 赖于如式(2)所示的精确观测模型,距离向和方位 向的耦合使得它的规模极其庞大,这使得如式(4) 所示 AMP 算法雷达成像面临高存储量大计算量的 问题,物理实现将非常困难。 2.2 基于近似观测模型的近似消息传递算法 通常情况下,典型的雷达成像算法如距离多普 勒算法、线调频变标算法等利用去耦合措施,能够有 效地解决高存储量和大计算量问题;同时,在复杂场 景的雷达回波的仿真中,利用逆线调频变标算子来 构造回波能够有效降低计算量。 鉴于此,本文试图 通过逆线调频变标算子来近似回波,同时结合采样 矩阵的 Kronecker 积形式,以期解决 AMP 算法在压 缩感知成像中遇到的高存储量大计算量问题。 由逆 线调频变标算法可知,式(2)所示观测矩阵 H 可以 使用式(5)所示逆线调频变标算子来近似表示[16] 。 H ≈ F H a P3F H r P2FrP1Fa (5) 式中:Fa ,Fr∈C N×N分别为方位向和距离向傅里叶变 换矩阵,它们都可以表示为 DFT 矩阵与单位矩阵的 Kronecker 积;对角矩阵 P1 、P2 、P3∈C N×N为逆线调频 变标过程中各步骤进行相位补偿的相位矩阵。 因 此,与观测矩阵有关的矩阵向量乘积可以表示为如 下的形式: Hx = vec(TICS(X));H H y = vec(TCS(Y)) (6) 式中:TCS(·)和 TICS(·)分别表示线调频变标算子 和逆线调频变标算子;X、Y 分别表示二维离散的观测 场景和二维离散回波矩阵。 因此,使用近似观测模型 的雷达成像可以转化为如式(7)所示的优化问题: arg min X λ ‖X‖1 + 1 2 ‖Y - ΘrTICS(X)Θa‖2 { 2} (7) 当雷达场景由少数强散射点构成时,X 可以认 为是一个具有空域稀疏性的稀疏信号,因此可以认 为目标服从拉普拉斯分布[17] ,同时,不失一般性,观 测噪声可以认为服从高斯分布,即 p(Xi) = exp( - βλ Xi ) p(Yj | X) = exp{ β 2 (Yj - (ΘrTICS(X)Θa )j) 2 } ì î í ïï ïï (8) 式中: (·)i 表示矩阵的第 i 个元素; β 为常数。 此时 可以构造如式(9)所示后验分布来解决式(7)所示 的优化问题。 p(X | Y) ≅ 1 Z∏ N i = 1 p(Xi)∏ m j = 1 p(Yj | X) (9) 式中 Z 为该分布的归一化常数。 当 β → ¥时,上述 分布将在式(7)所示的稀疏解处聚集。 这就意味着 只要能够求取上述分布的边缘概率密度分布,即可 获得式(7)所示优化问题的稀疏解,因此该雷达成 像问题的求解过程实际上就是 β → ¥时式(10)所示 分布边缘概率密度分布的求解过程。 虽然精确的求 取上述分布的边缘概率密度分布非常困难,但是通 过置信传播理论可以获得该边缘概率密度分布的近 似结果。 为了利用置信传播理论来求解边缘概率密度分 布,首先需要以 X1 ,X2 ,…,XN 作为变量节点,以 Y1 , Y2 ,…,Ym 作为因子节点,以任意变量节点和因子节 点之间的关系作为边构造双向因子图,然后可以通 过下述的和-积形式的置信传播理论来求取相应的 边缘概率密度分布: mi→j(Xi) ≅ p(Xi) k∈∏N(i) \j mk→i(Xi) mj→i(Xi) ≅ ∫ X-i p(Yj | X) k∈∏N(j) \i mk→j(Xi)dX-i ì î í ï ï ï ï (10) 式中: N(i) 表 示 与 节 点 i 相 邻 的 节 点 的 集 合, N(i) \j 表示除节点 j 以外与节点 i 相邻的节点的集 合,X-i表示除了 Xi 以外的所有变量节点,mi→j(Xi) 和 mj→i(Xi)为节点之间传递的消息。 则如式(9)所 示分布的边缘概率密度分布可以表示为 p(Xi | Y) = p(Xi) k∈∏N(i) mk→i(Xi) (11) 通过假设 mj→i(Xi)表征变量的三阶矩有界,可 知 mj→i(Xi ) 可以使用高斯分布进行近似,而 mi→j (Xi)可以近似认为具有高斯分布与拉普拉斯分布 的乘积形式,当 β → ¥时,通过一阶近似,基于近似 观测模型的置信传播算法可以通过下面的迭代过程 来实现,本文将该新算法称作基于近似观测模型的 AMP 算法。 X ^ t = TICS(Θ H r Z t-1Θ H a ) + X t-1 X t = μ(X ^ t ,λ + γ t ) Z t = Y - ΘrTCS(X t )Θa + 1 δ Z t-1 〈μ′(X ^ t ,λ + γ t )〉 γ t+1 = λ + γ t δ 〈μ′(X ^ t ,λ + γ t )〉 ì î í ï ï ï ï ï ï ï ï (12) 式中: μ(a,b) 表示软阈值算子, μ′(a,b) 为其一阶 导数; δ = m / N 表示数据采样率; 〈·〉 为求取均值。 上述算法流程可以正式描述如下: ·594· 智 能 系 统 学 报 第 10 卷
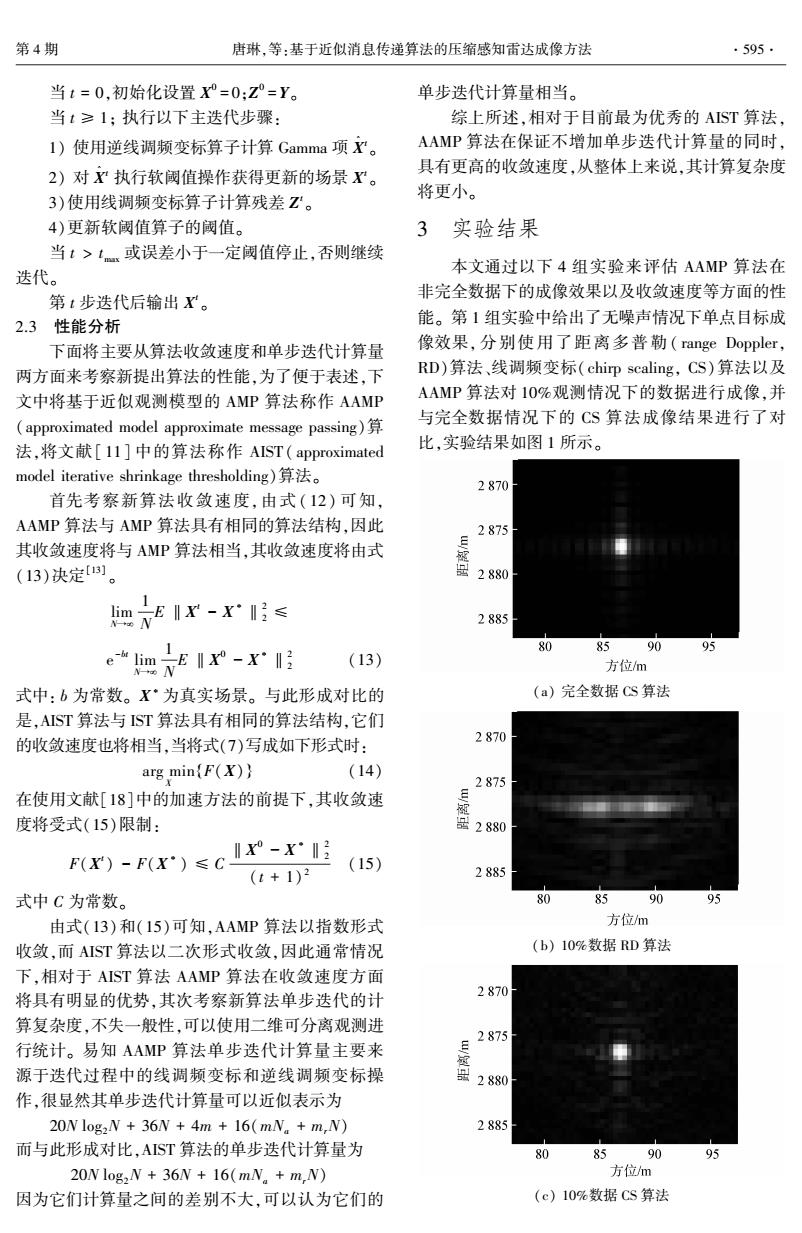
第4期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 ·595. 当t=0,初始化设置X°=0:Z°=Y。 单步迭代计算量相当。 当t≥1:执行以下主迭代步骤: 综上所述,相对于目前最为优秀的AST算法, 1)使用逆线调频变标算子计算Gamma项X。 AAMP算法在保证不增加单步迭代计算量的同时, 2)对X?执行软阈值操作获得更新的场景X。 具有更高的收敛速度,从整体上来说,其计算复杂度 3)使用线调频变标算子计算残差Z。 将更小。 4)更新软阈值算子的阈值。 3实验结果 当1>tm或误差小于一定阈值停止,否则继续 迭代。 本文通过以下4组实验来评估AAMP算法在 非完全数据下的成像效果以及收敛速度等方面的性 第t步迭代后输出X。 2.3性能分析 能。第1组实验中给出了无噪声情况下单点目标成 下面将主要从算法收敛速度和单步迭代计算量 像效果,分别使用了距离多普勒(range Doppler, 两方面来考察新提出算法的性能,为了便于表述,下 RD)算法、线调频变标(chirp scaling,CS)算法以及 文中将基于近似观测模型的AMP算法称作AAMP AAMP算法对10%观测情况下的数据进行成像,并 (approximated model approximate message passing) 与完全数据情况下的CS算法成像结果进行了对 法,将文献[l1]中的算法称作AIST(approximated 比,实验结果如图1所示。 model iterative shrinkage thresholding)算法。 2870 首先考察新算法收敛速度,由式(12)可知, AAMP算法与AMP算法具有相同的算法结构,因此 2875 其收敛速度将与AMP算法相当,其收敛速度将由式 (13)决定[] 盘2880 画NEIr-X:≤ 2885 。I-x月 80 8590 95 (13) 方位/m 式中:b为常数。X·为真实场景。与此形成对比的 (a)完全数据Cs算法 是,AST算法与ST算法具有相同的算法结构,它们 的收敛速度也将相当,当将式(7)写成如下形式时: 2870- arg min(F(X)) (14) 2875 在使用文献[18]中的加速方法的前提下,其收敛速 度将受式(15)限制: IX°-X13 F(X)-F(X·)≤C (15) (t+1)2 2885 式中C为常数。 80 85 90 95 由式(13)和(15)可知,AAMP算法以指数形式 方位m 收敛,而AST算法以二次形式收敛,因此通常情况 (b)10%数据RD算法 下,相对于AIST算法AAMP算法在收敛速度方面 将具有明显的优势,其次考察新算法单步迭代的计 2870 算复杂度,不失一般性,可以使用二维可分离观测进 2875 行统计。易知AAMP算法单步迭代计算量主要来 源于迭代过程中的线调频变标和逆线调频变标操 作,很显然其单步迭代计算量可以近似表示为 春 20N log2N 36N 4m 16(mN m,N) 2885 而与此形成对比,AST算法的单步迭代计算量为 80 85 90 95 20N log2N 36N 16(mN m,N) 方位m 因为它们计算量之间的差别不大,可以认为它们的 (c)10%数据CS算法
当 t = 0,初始化设置 X 0 = 0;Z 0 =Y。 当 t ≥ 1; 执行以下主迭代步骤: 1) 使用逆线调频变标算子计算 Gamma 项 X ^ t 。 2) 对 X ^ t 执行软阈值操作获得更新的场景 X t 。 3)使用线调频变标算子计算残差 Z t 。 4)更新软阈值算子的阈值。 当 t > tmax 或误差小于一定阈值停止,否则继续 迭代。 第 t 步迭代后输出 X t 。 2.3 性能分析 下面将主要从算法收敛速度和单步迭代计算量 两方面来考察新提出算法的性能,为了便于表述,下 文中将基于近似观测模型的 AMP 算法称作 AAMP (approximated model approximate message passing)算 法,将文献[ 11] 中的算法称作 AIST ( approximated model iterative shrinkage thresholding)算法。 首先考察新算法收敛速度,由式 ( 12) 可知, AAMP 算法与 AMP 算法具有相同的算法结构,因此 其收敛速度将与 AMP 算法相当,其收敛速度将由式 (13)决定[13] 。 lim N→¥ 1 N E ‖X t - X ∗‖2 2 ≤ e -bt lim N→¥ 1 N E ‖X 0 - X ∗‖2 2 (13) 式中: b 为常数。 X ∗ 为真实场景。 与此形成对比的 是,AIST 算法与 IST 算法具有相同的算法结构,它们 的收敛速度也将相当,当将式(7)写成如下形式时: arg min X {F(X)} (14) 在使用文献[18]中的加速方法的前提下,其收敛速 度将受式(15)限制: F(X t ) - F(X ∗ ) ≤ C ‖X 0 - X ∗‖2 2 (t + 1) 2 (15) 式中 C 为常数。 由式(13)和(15)可知,AAMP 算法以指数形式 收敛,而 AIST 算法以二次形式收敛,因此通常情况 下,相对于 AIST 算法 AAMP 算法在收敛速度方面 将具有明显的优势,其次考察新算法单步迭代的计 算复杂度,不失一般性,可以使用二维可分离观测进 行统计。 易知 AAMP 算法单步迭代计算量主要来 源于迭代过程中的线调频变标和逆线调频变标操 作,很显然其单步迭代计算量可以近似表示为 20N log2N + 36N + 4m + 16(mNa + mrN) 而与此形成对比,AIST 算法的单步迭代计算量为 20N log2N + 36N + 16(mNa + mrN) 因为它们计算量之间的差别不大,可以认为它们的 单步迭代计算量相当。 综上所述,相对于目前最为优秀的 AIST 算法, AAMP 算法在保证不增加单步迭代计算量的同时, 具有更高的收敛速度,从整体上来说,其计算复杂度 将更小。 3 实验结果 本文通过以下 4 组实验来评估 AAMP 算法在 非完全数据下的成像效果以及收敛速度等方面的性 能。 第 1 组实验中给出了无噪声情况下单点目标成 像效果, 分别使用了距离多普勒 ( range Doppler, RD)算法、线调频变标(chirp scaling, CS)算法以及 AAMP 算法对 10%观测情况下的数据进行成像,并 与完全数据情况下的 CS 算法成像结果进行了对 比,实验结果如图 1 所示。 (a) 完全数据 CS 算法 (b) 10%数据 RD 算法 (c) 10%数据 CS 算法 第 4 期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 ·595·
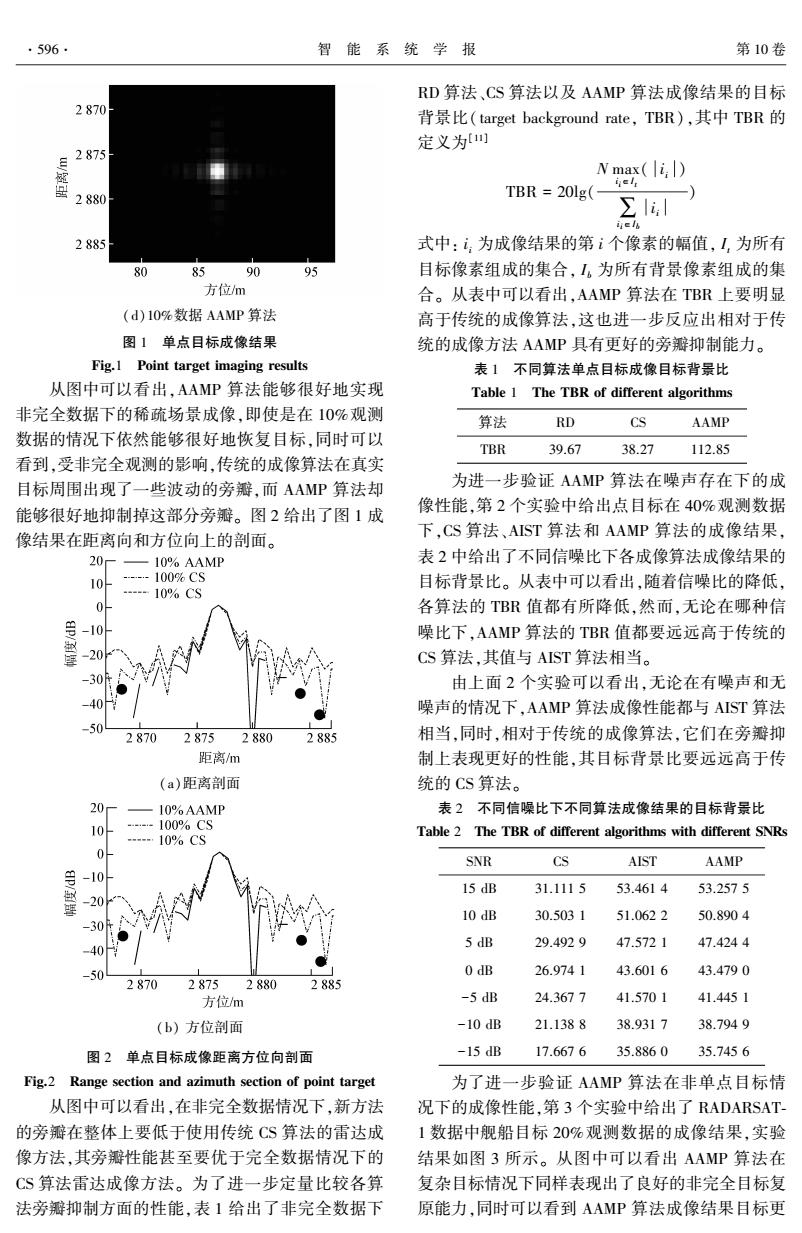
·596 智能系统学报 第10卷 RD算法、CS算法以及AAMP算法成像结果的目标 2870 背景比(target background rate,TBR),其中TBR的 定义为 2875 Nmax(i) 2880 TBR 20lg(- Σl, 2885 式中:,为成像结果的第i个像素的幅值,I,为所有 80 85 90 95 目标像素组成的集合,I。为所有背景像素组成的集 方位/m 合。从表中可以看出,AAMP算法在TBR上要明显 (d)10%数据AAMP算法 高于传统的成像算法,这也进一步反应出相对于传 图1单点目标成像结果 统的成像方法AAMP具有更好的旁瓣抑制能力。 Fig.I Point target imaging results 表1不同算法单点目标成像目标背景比 从图中可以看出,AAMP算法能够很好地实现 Table 1 The TBR of different algorithms 非完全数据下的稀疏场景成像,即使是在10%观测 算法 RD CS AAMP 数据的情况下依然能够很好地恢复目标,同时可以 TBR 39.67 38.27 112.85 看到,受非完全观测的影响,传统的成像算法在真实 目标周围出现了一些波动的旁瓣,而AAMP算法却 为进一步验证AAMP算法在噪声存在下的成 像性能,第2个实验中给出点目标在40%观测数据 能够很好地抑制掉这部分旁瓣。图2给出了图1成 像结果在距离向和方位向上的剖面。 下,CS算法、AIST算法和AAMP算法的成像结果, 20 —10%AAMP 表2中给出了不同信噪比下各成像算法成像结果的 10 --100%CS 目标背景比。从表中可以看出,随着信噪比的降低, 10%CS 0 各算法的TBR值都有所降低,然而,无论在哪种信 -10 噪比下,AAMP算法的TBR值都要远远高于传统的 型 204 CS算法,其值与AIST算法相当。 由上面2个实验可以看出,无论在有噪声和无 噪声的情况下,AAMP算法成像性能都与AIST算法 -50 2870 2875 2880 2885 相当,同时,相对于传统的成像算法,它们在旁瓣抑 距离m 制上表现更好的性能,其目标背景比要远远高于传 (a)距离剖面 统的CS算法。 20r 10%AAMP 表2不同信噪比下不同算法成像结果的目标背景比 10 --100%CS Table 2 The TBR of different algorithms with different SNRs -10%CS 0 SNR CS AIST AAMP -10 15 dB 31.1115 53.4614 53.2575 20 10 dB 30.5031 51.0622 50.8904 -30 40 5 dB 29.4929 47.5721 47.4244 50 0dB 26.9741 43.6016 43.4790 2870 2875 2880 2885 方位/m -5 dB 24.3677 41.5701 41.4451 (b)方位剖面 -10dB 21.1388 38.9317 38.7949 图2单点目标成像距离方位向剖面 -15dB 17.6676 35.8860 35.7456 Fig.2 Range section and azimuth section of point target 为了进一步验证AAMP算法在非单点目标情 从图中可以看出,在非完全数据情况下,新方法 况下的成像性能,第3个实验中给出了RADARSAT- 的旁瓣在整体上要低于使用传统CS算法的雷达成 1数据中舰船目标20%观测数据的成像结果,实验 像方法,其旁瓣性能甚至要优于完全数据情况下的 结果如图3所示。从图中可以看出AAMP算法在 CS算法雷达成像方法。为了进一步定量比较各算 复杂目标情况下同样表现出了良好的非完全目标复 法旁瓣抑制方面的性能,表1给出了非完全数据下 原能力,同时可以看到AAMP算法成像结果目标更
(d)10%数据 AAMP 算法 图 1 单点目标成像结果 Fig.1 Point target imaging results 从图中可以看出,AAMP 算法能够很好地实现 非完全数据下的稀疏场景成像,即使是在 10%观测 数据的情况下依然能够很好地恢复目标,同时可以 看到,受非完全观测的影响,传统的成像算法在真实 目标周围出现了一些波动的旁瓣,而 AAMP 算法却 能够很好地抑制掉这部分旁瓣。 图 2 给出了图 1 成 像结果在距离向和方位向上的剖面。 (a)距离剖面 (b) 方位剖面 图 2 单点目标成像距离方位向剖面 Fig.2 Range section and azimuth section of point target 从图中可以看出,在非完全数据情况下,新方法 的旁瓣在整体上要低于使用传统 CS 算法的雷达成 像方法,其旁瓣性能甚至要优于完全数据情况下的 CS 算法雷达成像方法。 为了进一步定量比较各算 法旁瓣抑制方面的性能,表 1 给出了非完全数据下 RD 算法、CS 算法以及 AAMP 算法成像结果的目标 背景比( target background rate, TBR),其中 TBR 的 定义为[11] TBR = 20lg( N max i i∈I t ( i i ) ∑i i∈Ib i i ) 式中: i i 为成像结果的第 i 个像素的幅值, It 为所有 目标像素组成的集合, Ib 为所有背景像素组成的集 合。 从表中可以看出,AAMP 算法在 TBR 上要明显 高于传统的成像算法,这也进一步反应出相对于传 统的成像方法 AAMP 具有更好的旁瓣抑制能力。 表 1 不同算法单点目标成像目标背景比 Table 1 The TBR of different algorithms 算法 RD CS AAMP TBR 39.67 38.27 112.85 为进一步验证 AAMP 算法在噪声存在下的成 像性能,第 2 个实验中给出点目标在 40%观测数据 下,CS 算法、AIST 算法和 AAMP 算法的成像结果, 表 2 中给出了不同信噪比下各成像算法成像结果的 目标背景比。 从表中可以看出,随着信噪比的降低, 各算法的 TBR 值都有所降低,然而,无论在哪种信 噪比下,AAMP 算法的 TBR 值都要远远高于传统的 CS 算法,其值与 AIST 算法相当。 由上面 2 个实验可以看出,无论在有噪声和无 噪声的情况下,AAMP 算法成像性能都与 AIST 算法 相当,同时,相对于传统的成像算法,它们在旁瓣抑 制上表现更好的性能,其目标背景比要远远高于传 统的 CS 算法。 表 2 不同信噪比下不同算法成像结果的目标背景比 Table 2 The TBR of different algorithms with different SNRs SNR CS AIST AAMP 15 dB 31.111 5 53.461 4 53.257 5 10 dB 30.503 1 51.062 2 50.890 4 5 dB 29.492 9 47.572 1 47.424 4 0 dB 26.974 1 43.601 6 43.479 0 -5 dB 24.367 7 41.570 1 41.445 1 -10 dB 21.138 8 38.931 7 38.794 9 -15 dB 17.667 6 35.886 0 35.745 6 为了进一步验证 AAMP 算法在非单点目标情 况下的成像性能,第 3 个实验中给出了 RADARSAT⁃ 1 数据中舰船目标 20%观测数据的成像结果,实验 结果如图 3 所示。 从图中可以看出 AAMP 算法在 复杂目标情况下同样表现出了良好的非完全目标复 原能力,同时可以看到 AAMP 算法成像结果目标更 ·596· 智 能 系 统 学 报 第 10 卷
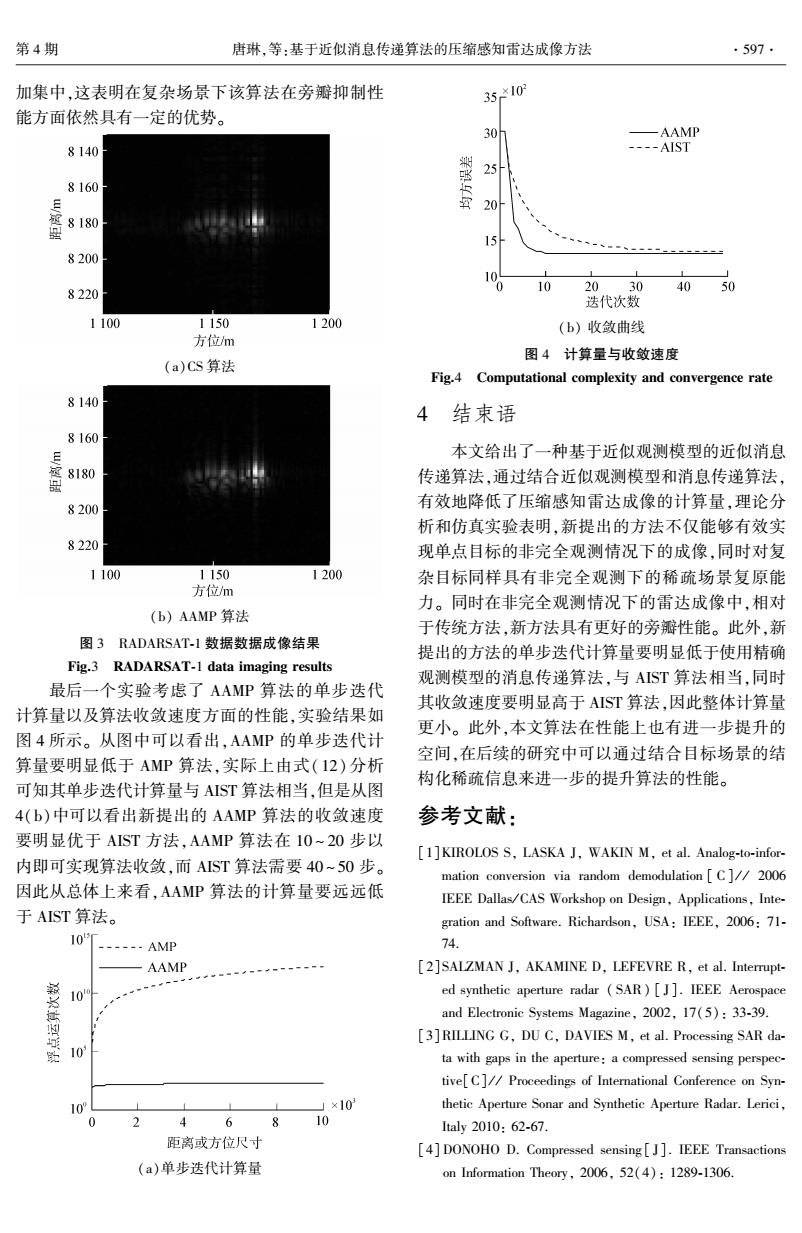
第4期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 .597. 加集中,这表明在复杂场景下该算法在旁瓣抑制性 35*10 能方面依然具有一定的优势。 30h -AAMP 8140 ----AIST 25 8160 e网 20 15 8200 8220 10 20. 30 40 50 迭代次数 1100 1150 1200 (b)收敛曲线 方位m 图4计算量与收敛速度 (a)Cs算法 Fig.4 Computational complexity and convergence rate 8140 4结束语 8160 本文给出了一种基于近似观测模型的近似消息 室8180 传递算法,通过结合近似观测模型和消息传递算法, 8200- 有效地降低了压缩感知雷达成像的计算量,理论分 析和仿真实验表明,新提出的方法不仅能够有效实 8220 现单点目标的非完全观测情况下的成像,同时对复 1100 1150 1200 杂目标同样具有非完全观测下的稀疏场景复原能 方位m 力。同时在非完全观测情况下的雷达成像中,相对 (b)AAMP算法 于传统方法,新方法具有更好的旁瓣性能。此外,新 图3 RADARSAT-1数据数据成像结果 提出的方法的单步迭代计算量要明显低于使用精确 Fig.3 RADARSAT-1 data imaging results 观测模型的消息传递算法,与AST算法相当,同时 最后一个实验考虑了AAMP算法的单步迭代 其收敛速度要明显高于AIST算法,因此整体计算量 计算量以及算法收敛速度方面的性能,实验结果如 更小。此外,本文算法在性能上也有进一步提升的 图4所示。从图中可以看出,AAMP的单步迭代计 空间,在后续的研究中可以通过结合目标场景的结 算量要明显低于AMP算法,实际上由式(12)分析 构化稀疏信息来进一步的提升算法的性能。 可知其单步迭代计算量与AST算法相当,但是从图 4(b)中可以看出新提出的AAMP算法的收敛速度 参考文献: 要明显优于AIST方法,AAMP算法在10~20步以 [1]KIROLOS S,LASKA J,WAKIN M,et al.Analog-to-infor- 内即可实现算法收敛,而AIST算法需要40~50步。 mation conversion via random demodulation C]//2006 因此从总体上来看,AAMP算法的计算量要远远低 IEEE Dallas/CAS Workshop on Design,Applications,Inte- 于AIST算法。 gration and Software.Richardson,USA:IEEE,2006:71- 10T -----AMP 74. AAMP [2]SALZMAN J,AKAMINE D,LEFEVRE R,et al.Interrupt- 10 ed synthetic aperture radar (SAR)[J].IEEE Aerospace and Electronie Systems Magazine,2002,17(5):33-39. [3]RILLING G,DU C,DAVIES M,et al.Processing SAR da- 贸 10 ta with gaps in the aperture:a compressed sensing perspec- tive[C]//Proceedings of International Conference on Syn- 10 」×10 thetic Aperture Sonar and Synthetic Aperture Radar.Lerici, 0 46 8 10 Italy2010:62-67. 距离或方位尺寸 [4]DONOHO D.Compressed sensing [J].IEEE Transactions (a)单步选代计算量 on Information Theory,2006,52(4):1289-1306
加集中,这表明在复杂场景下该算法在旁瓣抑制性 能方面依然具有一定的优势。 (a)CS 算法 (b) AAMP 算法 图 3 RADARSAT⁃1 数据数据成像结果 Fig.3 RADARSAT⁃1 data imaging results 最后一个实验考虑了 AAMP 算法的单步迭代 计算量以及算法收敛速度方面的性能,实验结果如 图 4 所示。 从图中可以看出,AAMP 的单步迭代计 算量要明显低于 AMP 算法,实际上由式(12) 分析 可知其单步迭代计算量与 AIST 算法相当,但是从图 4(b)中可以看出新提出的 AAMP 算法的收敛速度 要明显优于 AIST 方法,AAMP 算法在 10 ~ 20 步以 内即可实现算法收敛,而 AIST 算法需要 40 ~ 50 步。 因此从总体上来看,AAMP 算法的计算量要远远低 于 AIST 算法。 (a)单步迭代计算量 (b) 收敛曲线 图 4 计算量与收敛速度 Fig.4 Computational complexity and convergence rate 4 结束语 本文给出了一种基于近似观测模型的近似消息 传递算法,通过结合近似观测模型和消息传递算法, 有效地降低了压缩感知雷达成像的计算量,理论分 析和仿真实验表明,新提出的方法不仅能够有效实 现单点目标的非完全观测情况下的成像,同时对复 杂目标同样具有非完全观测下的稀疏场景复原能 力。 同时在非完全观测情况下的雷达成像中,相对 于传统方法,新方法具有更好的旁瓣性能。 此外,新 提出的方法的单步迭代计算量要明显低于使用精确 观测模型的消息传递算法,与 AIST 算法相当,同时 其收敛速度要明显高于 AIST 算法,因此整体计算量 更小。 此外,本文算法在性能上也有进一步提升的 空间,在后续的研究中可以通过结合目标场景的结 构化稀疏信息来进一步的提升算法的性能。 参考文献: [1]KIROLOS S, LASKA J, WAKIN M, et al. Analog⁃to⁃infor⁃ mation conversion via random demodulation [ C] / / 2006 IEEE Dallas/ CAS Workshop on Design, Applications, Inte⁃ gration and Software. Richardson, USA: IEEE, 2006: 71⁃ 74. [2]SALZMAN J, AKAMINE D, LEFEVRE R, et al. Interrupt⁃ ed synthetic aperture radar ( SAR) [ J]. IEEE Aerospace and Electronic Systems Magazine, 2002, 17(5): 33⁃39. [3]RILLING G, DU C, DAVIES M, et al. Processing SAR da⁃ ta with gaps in the aperture: a compressed sensing perspec⁃ tive[C] / / Proceedings of International Conference on Syn⁃ thetic Aperture Sonar and Synthetic Aperture Radar. Lerici, Italy 2010: 62⁃67. [4] DONOHO D. Compressed sensing [ J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289⁃1306. 第 4 期 唐琳,等:基于近似消息传递算法的压缩感知雷达成像方法 ·597·

.598. 智能系统学报 第10卷 [5]谢晓春.压缩感知理论在雷达成像中的应用研究[D]. [14]HIRABAYASHI A,SUGIMOTO J,MIMURA K.Approxi- 北京:中国科学院研究生院,2010:100-102. mate message passing algorithm for complex separable com- XIE Xiaochun.Study on the application of Compressive pressed imaging[C]//2013 Asia-Pacific Signal and Infor- Sensing in radar imaging D.Beijing:Chinese Academy of mation Processing Association Annual Summit and Confer- Sciences,.2010:100-102. ence (APSIPA).Kaohsiung,China:IEEE,2013:1-5. [6]全英汇.稀疏信号处理在达检测和成像中的应用研究 [15]MALEKI A,ANITORI L,YANG Z,et al.asymptotic a- [D].西安:西安电子科技大学,2012:46-49. nalysis of complex Lasso via complex approximate message QUAN Yinghui.Study on sparse signal processing for radar passing (Camp)[J].IEEE Transactions on Information detection and imaging application[D].Xi'an:Xidian Uni- Theory,2013,59(7):4290-4308. versity,2012:46-49. [16]RANEY R K,RUNGE H,BAMLER R,et al.Precision [7]POTTER L C,ERTIN E,PARKER JT,et al.Sparsity and SAR processing using chirp scaling[J].IEEE Transactions compressed sensing in radar imaging[J].Proceedings of the on Geoscience and Remote Sensing,1994,32(4):786- IEEE,2010,98(6):1006-1020. 799. [8]TELLO A M,LOPEZ-DEKKER P,MALLORQUI J J.A [17]SEEGER M W.Bayesian inference and optimal design for novel strategy for radar imaging based on compressive sens- the sparse linear model[J].Journal of Machine Learning ing [J].IEEE Transactions on Geoscience and Remote Research.2008.9:759-813. Sensing,.2010,48(12):4285-4295. [18]BECK A,TEBOULLE M.A fast iterative shrinkage-thresh- [9]PATEL V M,EASLEY G R,HEALY JR D M,et al.Com- olding algorithm for linear inverse problems[J].SIAM pressed synthetic aperture radar[J].IEEE Joural of Select- Journal on Imaging Sciences,2009,2(1):183-202. ed Topics in Signal Processing,2010,4(2):244-254. 作者简介: [10]ZHANG B C,JIANG H,Hong W,et al.Synthetic aper- 唐琳,男,1987年生,博士,主要研 ture radar imaging of sparse targets via compressed sensing 究方向为雷达信号处理、雷达成像。 [C]//2010 8th European Conference on Synthetic Aper- ture Radar (EUSAR).Aachen,Germany:VDE,2010:1- 4 [11]DONG X,ZHANG Y H.A novel compressive sensing al- gorithm for SAR imaging [J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 焦淑红,女,1966年生,教授,博士 2014.7(2):708-720. 生导师,中国图像图形学会会员,黑龙 [12]FANG J,XU Z B,ZHANG B C,et al.Fast compressed 江省生物医学工程学会会员。主要研 sensing sar imaging based on approximated observation[J]. 究方向为图像处理与机器视觉、精确制 IEEE Journal of Selected Topics in Applied Earth Observa- 导与定位。 tions and Remote Sensing,2014,7(1):352-363. [13]MALEKI A.Approximate message passing algorithms for compressed sensing[D]Stanford,USA:Stanford Universi- [责任编辑:刘畅] ty,2011:103-115
[5]谢晓春. 压缩感知理论在雷达成像中的应用研究[D]. 北京: 中国科学院研究生院, 2010: 100⁃102. XIE Xiaochun. Study on the application of Compressive Sensing in radar imaging[D]. Beijing: Chinese Academy of Sciences, 2010: 100⁃102. [6]全英汇. 稀疏信号处理在雷达检测和成像中的应用研究 [D]. 西安: 西安电子科技大学, 2012: 46⁃49. QUAN Yinghui. Study on sparse signal processing for radar detection and imaging application[D]. Xi’ an: Xidian Uni⁃ versity, 2012: 46⁃49. [7]POTTER L C, ERTIN E, PARKER J T, et al. Sparsity and compressed sensing in radar imaging[J]. Proceedings of the IEEE, 2010, 98(6): 1006⁃1020. [8] TELLO A M, LOPEZ⁃DEKKER P, MALLORQUI J J. A novel strategy for radar imaging based on compressive sens⁃ ing [ J ]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285⁃4295. [9]PATEL V M, EASLEY G R, HEALY JR D M, et al. Com⁃ pressed synthetic aperture radar[J]. IEEE Journal of Select⁃ ed Topics in Signal Processing, 2010, 4(2): 244⁃254. [10]ZHANG B C, JIANG H, Hong W, et al. Synthetic aper⁃ ture radar imaging of sparse targets via compressed sensing [C] / / 2010 8th European Conference on Synthetic Aper⁃ ture Radar (EUSAR). Aachen, Germany: VDE, 2010: 1⁃ 4. [11]DONG X, ZHANG Y H. A novel compressive sensing al⁃ gorithm for SAR imaging [ J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(2): 708⁃720. [12]FANG J, XU Z B, ZHANG B C, et al. Fast compressed sensing sar imaging based on approximated observation[J]. IEEE Journal of Selected Topics in Applied Earth Observa⁃ tions and Remote Sensing, 2014, 7(1): 352⁃363. [13] MALEKI A. Approximate message passing algorithms for compressed sensing[D]Stanford, USA: Stanford Universi⁃ ty, 2011: 103⁃115. [14]HIRABAYASHI A, SUGIMOTO J, MIMURA K. Approxi⁃ mate message passing algorithm for complex separable com⁃ pressed imaging[C] / / 2013 Asia⁃Pacific Signal and Infor⁃ mation Processing Association Annual Summit and Confer⁃ ence (APSIPA). Kaohsiung, China: IEEE, 2013: 1⁃5. [15]MALEKI A, ANITORI L, YANG Z, et al. asymptotic a⁃ nalysis of complex Lasso via complex approximate message passing ( Camp) [ J]. IEEE Transactions on Information Theory, 2013, 59(7): 4290⁃4308. [16] RANEY R K, RUNGE H, BAMLER R, et al. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32( 4): 786⁃ 799. [17]SEEGER M W. Bayesian inference and optimal design for the sparse linear model[ J]. Journal of Machine Learning Research, 2008, 9: 759⁃813. [18]BECK A, TEBOULLE M. A fast iterative shrinkage⁃thresh⁃ olding algorithm for linear inverse problems [ J ]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183⁃202. 作者简介: 唐琳,男,1987 年生,博士,主要研 究方向为雷达信号处理、雷达成像。 焦淑红,女,1966 年生,教授,博士 生导师,中国图像图形学会会员,黑龙 江省生物医学工程学会会员。 主要研 究方向为图像处理与机器视觉、精确制 导与定位。 [责任编辑:刘畅] ·598· 智 能 系 统 学 报 第 10 卷